装配生产线位置控制系统设计

冯强

摘要：本文以减震部件装配生产线为研究对象，采用双环+前馈的控制方式，利用伺服驱动器本身构成速度环控制，利用位置控制器构成位置环控制，建立了位置控制系统的传递函数，利用工程设计法把系统分别校正为Ⅰ型系统和Ⅱ型系统。对采用PID控制算法和前馈+反馈控制算法时系统的控制性能進行了分析比较，通过MATLAB/SIMULINK仿真验证了采用位置反馈+前馈控制算法对位置控制系统的精度和响应速度有所提高。

关键词：位置控制系统;反馈+前馈控制;自动化装配系统

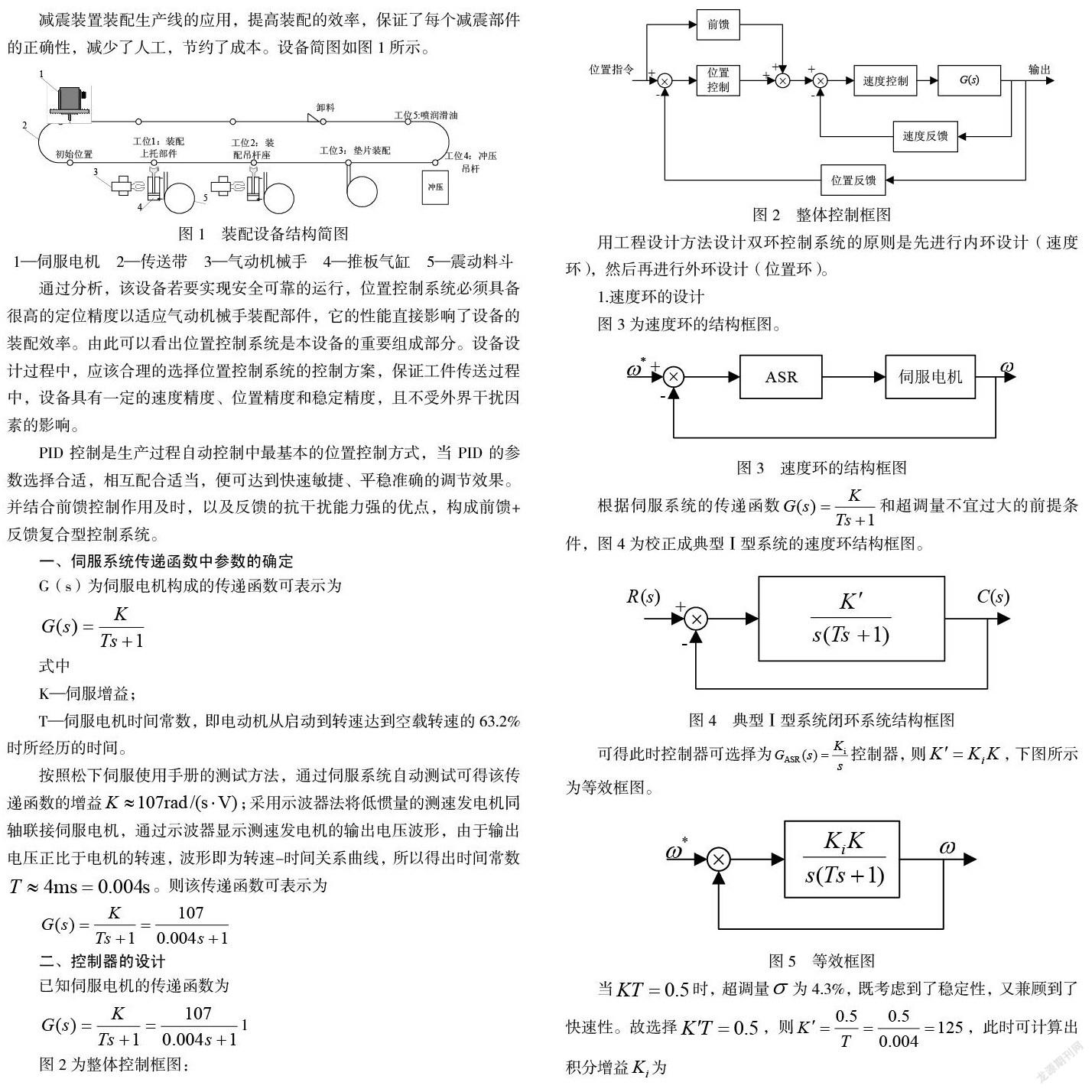
减震装置装配生产线的应用，提高装配的效率，保证了每个减震部件的正确性，减少了人工，节约了成本。设备简图如图1所示。

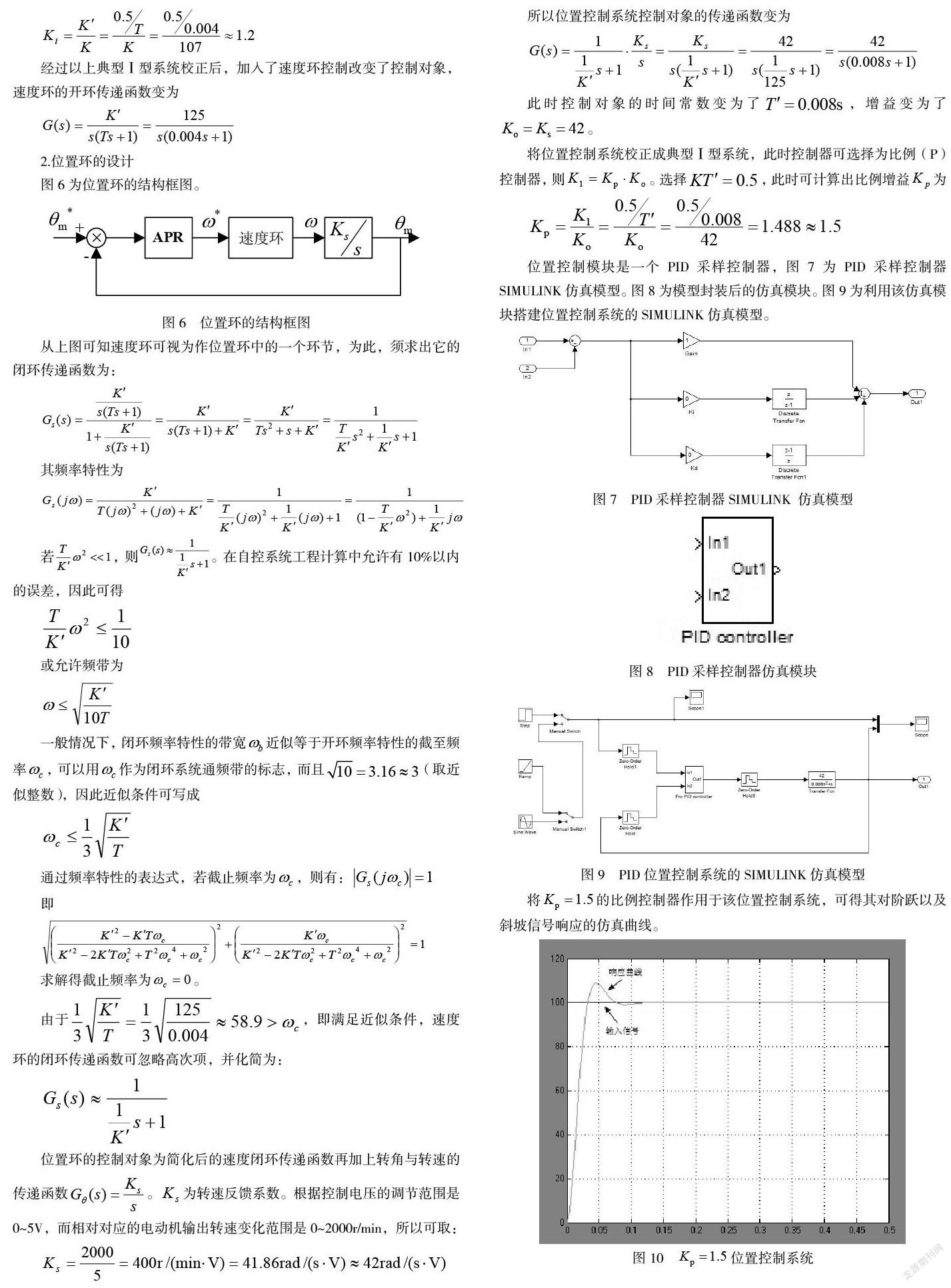
通过分析，该设备若要实现安全可靠的运行，位置控制系统必须具备很高的定位精度以适应气动机械手装配部件，它的性能直接影响了设备的装配效率。由此可以看出位置控制系统是本设备的重要组成部分。设备设计过程中，应该合理的选择位置控制系统的控制方案，保证工件传送过程中，设备具有一定的速度精度、位置精度和稳定精度，且不受外界干扰因素的影响。

PID控制是生产过程自动控制中最基本的位置控制方式，当PID的参数选择合适，相互配合适当，便可达到快速敏捷、平稳准确的调节效果。并结合前馈控制作用及时，以及反馈的抗干扰能力强的优点，构成前馈+反馈复合型控制系统。

一、伺服系统传递函数中参数的确定

按照松下伺服使用手册的测试方法，通过伺服系统自动测试可得该传递函数的增益 ;采用示波器法将低惯量的测速发电机同轴联接伺服电机，通过示波器显示测速发电机的输出电压波形，由于输出电压正比于电机的转速，波形即为转速-时间关系曲线，所以得出时间常数 。则该传递函数可表示为

二、控制器的设计

从图10中可以清楚的看到，当 时，位置控制系统对阶跃信号的响应速度快，而超调量却减小了，调节时间也变得很小，且没有稳态误差，控制效果良好。因此，位置环控制系统应采用校正为典型Ⅰ型系统。

位置前馈算法是现在位置控制系统中常用的一种控制方法，它能够消除斜波信号的稳态误差，并提高响应速度。

三、前馈+反馈的复合控制

1.前向差分控制

图12表示前馈控制算法。

2.前馈+反馈复合控制器

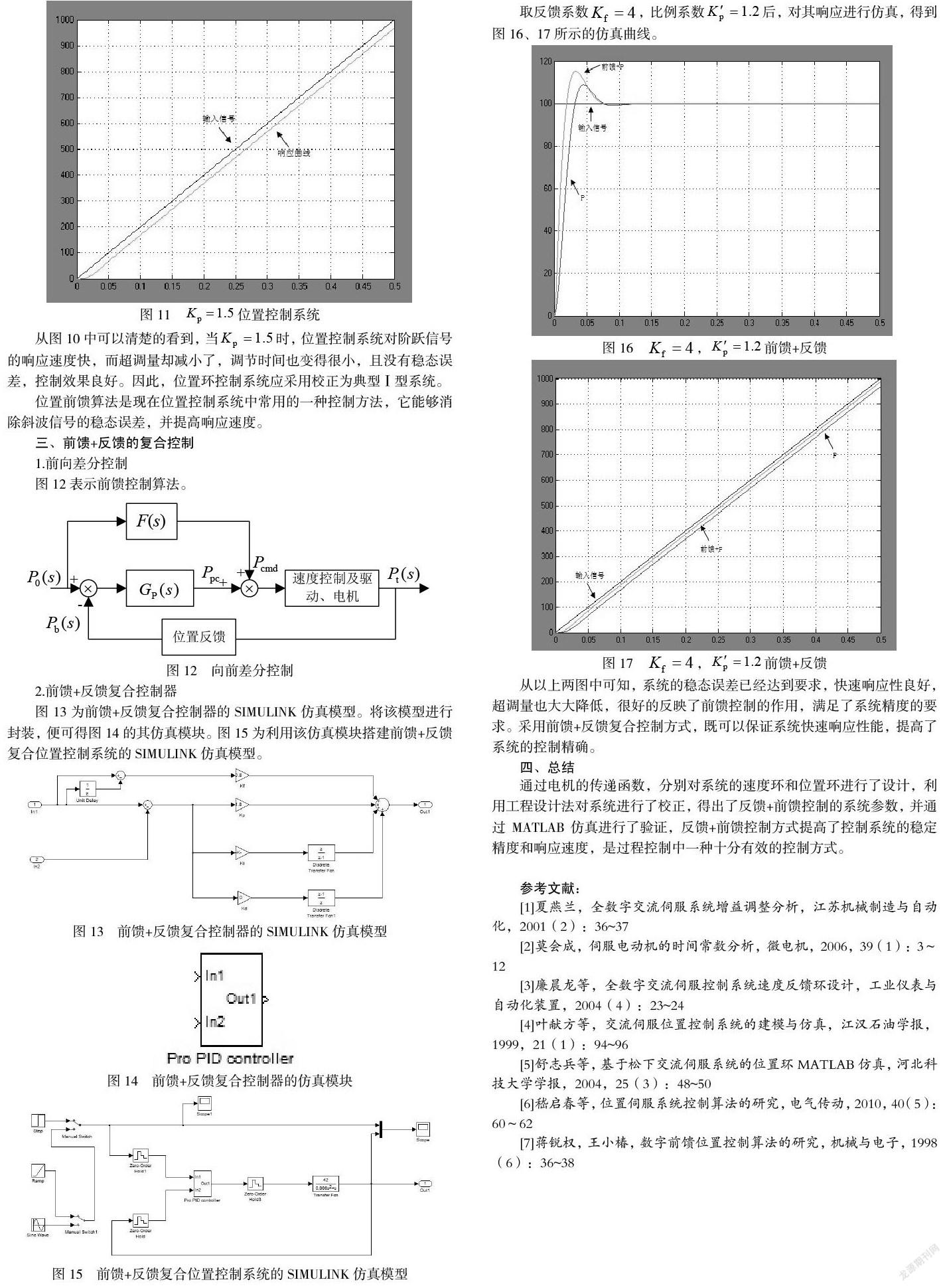
图13为前馈+反馈复合控制器的SIMULINK仿真模型。将该模型进行封装，便可得图14的其仿真模块。图15为利用该仿真模块搭建前馈+反馈复合位置控制系统的SIMULINK仿真模型。

从以上两图中可知，系统的稳态误差已经达到要求，快速响应性良好，超调量也大大降低，很好的反映了前馈控制的作用，满足了系统精度的要求。采用前馈+反馈复合控制方式，既可以保证系统快速响应性能，提高了系统的控制精确。

四、总结

通过电机的传递函数，分别对系统的速度环和位置环进行了设计，利用工程设计法对系统进行了校正，得出了反馈+前馈控制的系统参数，并通过MATLAB仿真进行了验证，反馈+前馈控制方式提高了控制系统的稳定精度和响应速度，是过程控制中一种十分有效的控制方式。

参考文献：

[1]夏燕兰，全数字交流伺服系统增益调整分析，江苏机械制造与自动化，2001（2）：36～37

[2]莫会成，伺服电动机的时间常数分析，微电机，2006，39（1）：3～12

[3]廉晨龙等，全数字交流伺服控制系统速度反馈环设计，工业仪表与自动化装置，2004（4）：23～24

[4]叶献方等，交流伺服位置控制系统的建模与仿真，江汉石油学报，1999，21（1）：94～96

[5]舒志兵等，基于松下交流伺服系统的位置环MATLAB仿真，河北科技大学学报，2004，25（3）：48～50

[6]嵇启春等，位置伺服系统控制算法的研究，电气传动，2010，40（5）：60～62

[7]蒋锐权，王小椿，数字前馈位置控制算法的研究，机械与电子，1998（6）：36～38