基于参数辨识的水下推进永磁同步电机无位置传感器控制
陈尧伟,曾庆军,戴晓强,吴 伟,李宏宇,姚震球
基于参数辨识的水下推进永磁同步电机无位置传感器控制
陈尧伟1,曾庆军1,戴晓强1,吴 伟1,李宏宇1,姚震球2
(1. 江苏科技大学 电子信息学院,江苏镇江,212003; 2. 江苏科技大学 海洋装备研究院,江苏镇江,212003)
针对水下推进器在运行过程中,永磁同步电机的定子电阻、电感等参数会受到温度、电流变化而导致的无位置控制算法估算转子位置和速度出现较大误差的问题,提出了一种基于参数辨识的龙伯格观测器水下推进器无位置传感器控制方法。该方法在双闭环矢量控制的基础上,采用带遗忘因子的递推最小二乘法作为参数辨识算法,通过在线辨识得到电机定子电阻和电感参数,将其取代龙伯格观测器模型中的初始电阻和电感参数,龙伯格观测器估算得到的反电动势作为锁相环的输入,最终,由锁相环输出得到转子的位置和速度。仿真结果表明,基于参数辨识的龙伯格观测器在受到参数变化干扰后,能快速准确地辨识出转子位置和速度信息,降低了无位置控制系统对电机参数的敏感性。
水下推进器; 永磁同步电机; 龙伯格观测器; 参数辨识; 递推最小二乘法; 敏感性
0 引言
近年来,随着我国对海洋资源的关注度越来越高,水下机器人、水面无人艇以及水下滑翔机等航行器也得到了很大的发展。为实现航行器在广阔而复杂的海洋环境中长时间安全稳定的作业,就必须对水下推进系统提出更高的性能要求。永磁同步电机(permanent magnet synchronous motor,PMSM)作为水下推进器的核心动力设备,因具有结构简单、可靠性高、功率密度大等优点,具有良好的应用前景[1]。
PMSM目前常见的控制方式是无位置传感器控制结合空间矢量脉宽调制(space vector pulse width modulation,SVPWM)控制。由于水下工况复杂,环境恶劣,以及PMSM自身结构及功率密度的限制,电机参数严重影响无位置传感器算法的控制性能,降低了控制系统的稳定性。对此,国内外学者提出参数辨识的概念和大量辨识理论方法[2]。陈再发等[3]通过模型参考自适应方法在线辨识电机参数,运用Runge-Kutta方法建立满秩可调模型。金宁治等[4]针对内置式PMSM提出了一种在线辨识定子交轴电感、转子磁链的模型参考自适应系统(model reference adaptive system,MRAS)参数辨识方法,解决了模型欠秩问题。刘细平等[5]提出一种将小生镜策略和混沌变异策略相结合的混沌变异小生境粒子群算法(niche chaos particle swarm optimization,NCPSO),同时辨识了4个参数,分别是定子绕组电阻,定子绕组轴轴电感以及永磁体磁链。荆禄宗等[6]在采用变分理论实现最小绝对值偏差法(least absolute deviations,LAD)的基础上,研究了一种基于递归神经网络(recursion neural network,RNN)的辨识方法。董召强等[7]采用最小二乘法(recursive least square,RLS)在线辨识电机参数,并在硬件上实现辨识算法。
文中的研究对象为表贴式PMSM,采用龙伯格观测器的无位置传感器控制,结合了一种带有遗忘因子的RLS辨识方法,并通过电压瞬态方程构建辨识模型,辨识得到电机的定子电阻和电感值,将其取代龙伯格观测器模型的初始电机参数,从而得到对参数不敏感的龙伯格观测器,继而得到更准确的转子位置和转速信息,最后对设计的辨识方法进行了仿真验证。
1 水下推进PMSM
1.1 水下推进器原理
如图1所示,相较于传统的水下推进器,一体式水下推进器是将导流罩、减速器、螺旋桨、连接轴和电机等集成的水下动力系统,具有质量轻、工作噪声小、散热性能好、功率密度大、动力传输效果好等优点,常适合作为水下机器人、水面快艇和水上无人艇的推进系统。

图1 水下推进器原理及实物图
PMSM转子连接磁耦合器的输入轴,由PMSM带动磁耦合器转动,磁耦合器的输出轴连接螺旋桨,使螺旋桨与电机转子同步转动,进而实现由电机到螺旋桨的电力传动。导管能够将桨叶的尾涡转化为导管的附着涡,有效起到整流作用,增大了推力。磁耦合器可以有效地隔离海水,从而实现水下推进器的静密封。
1.2 水下推进PMSM数学模型
取逆时针方向为电机旋转的正方向,按照电动机原则建立PMSM数学模型。PMSM三相绕组的电压方程可以表示为[8]
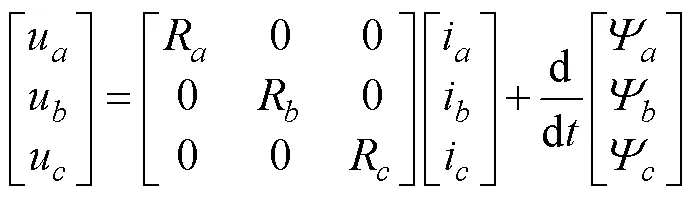

由于PMSM在三相坐标系中的数学模型是一个多变量、强耦合以及非线性的系统,很难对其进行控制,因此,需对其进行坐标变换,变为两相静止坐标系。则PMSM在两相静止坐标系下的数学模型为[9]


在磁场等效的基础上,将两相静止坐标系转换为两相旋转坐标系。则PMSM在两相旋转坐标系下的电压数学模型为[10]

2 龙伯格观测器设计
龙伯格观测器辨识转子位置的基本思路为,利用给定电流和反馈电流之间的误差来重构电机的反电动势,即将实际电流值与估算电流值的误差作为输入,输出得到反电动势估计值,用两反电动势相位关系,通过锁相环估算转子位置和速度。
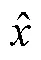
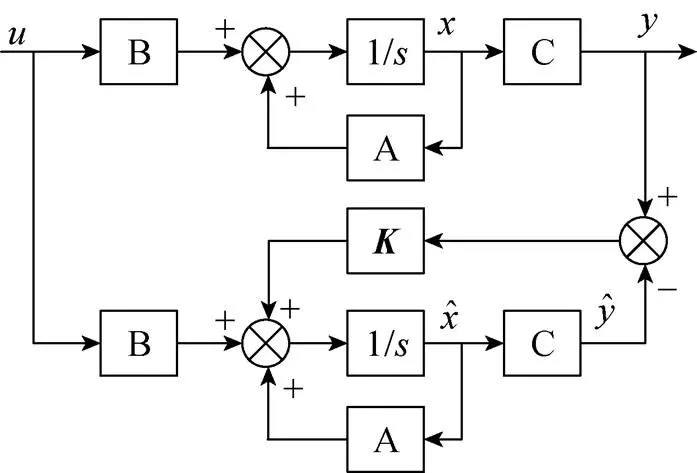
图2 渐进状态观测器原理图
由式(3)可知,PMSM在两相静止坐标系下的电压方程中含有转子速度和位置信息,根据该模型设计PMSM龙伯格观测器。对反电动势做微分,并以矩阵的形式表达电机数学模型,可以得到

根据渐进状态观测器原理图,可建立龙伯格观测器模型为

龙伯格观测器设计原理如图3所示。

图3 龙伯格观测器原理图
将龙伯格观测器估算得到的反电动势作为锁相环的输入,由锁相环输出得到转子的位置和速度。
3 基于参数辨识的龙伯格观测器设计
由于水下环境恶劣,且水下推进器大多是低压大功率类型,所以有较大的电机相电流,会出现明显的发热现象,而电机参数中定子电阻受温升影响最大,电感受磁路饱和影响最大,根据式(7)可知,龙伯格观测器模型是以电机初始的定子电阻和电感参数建立的,所以参数的变化会严重影响无位置传感器控制性能。因RLS具有算法简单、易于实现等优点,文中将使用带遗忘因子的RLS在线辨识电机的定子电阻和电感参数,并将其取代龙伯格观测器中的初始电机参数[12-13]。
3.1 带遗忘因子的RLS
系统的输入量和输出量可以表示为

递推RLS是指当被辨识系统运行时,利用新引入的观测数据对前次估计的结果不断进行修正,得出新的参数估计值,减少估计误差,直到参数估计值达到满意的精确程度[14-15]。
构建目标函数
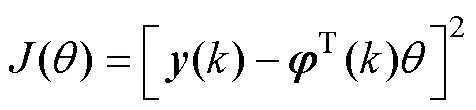
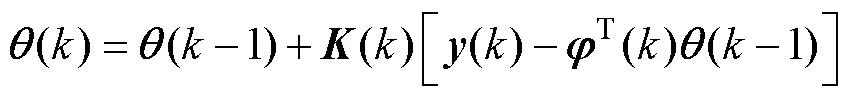
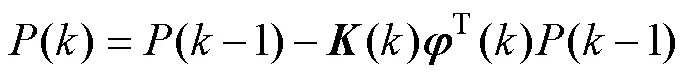
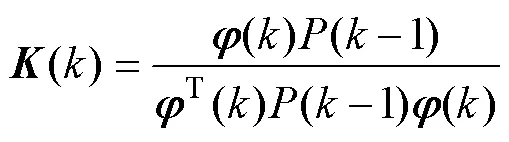
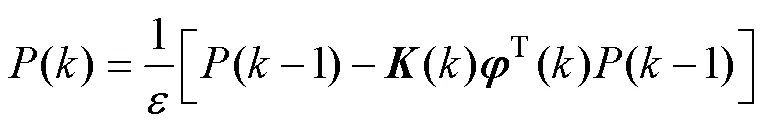

3.2 带遗忘因子的RLS参数辨识

由于文中采用i=0的控制方式,所以式(15)变为
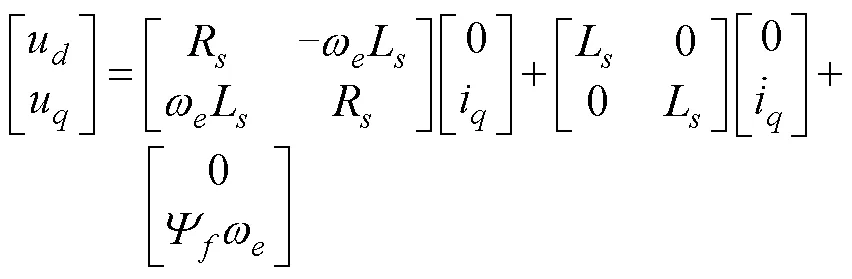
由式(16)可知,基于旋转坐标系下的电机模型最多只能同时辨识1个参数,故若想辨识得到2个参数,可以增加额外的方程或者减少辨识参数。
为了辨识2个参数,采用分步辨识方法。由于温敏参数电阻的变化速率远远小于电感,所以在每个周期内,将电阻值作为定值,辨识得到电感的估算值; 每10个周期内,将电感值作为定值,辨识得到电阻的估算值,以此循环更新。
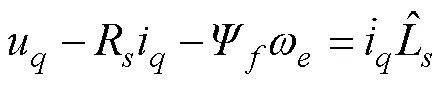
对式(17)进行离散化处理,得到

根据式(8)和式(18),可以得到



得到带遗忘因子的RLS辨识电机电感的递推公式
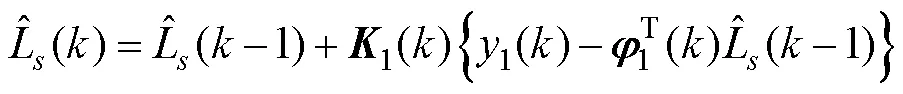

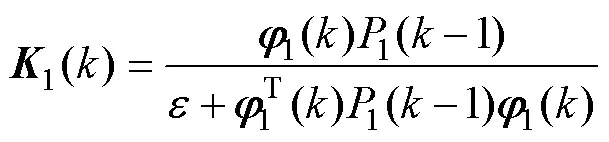

对式(25)进行离散化处理,得到

根据式(8)和式(26),可以得到
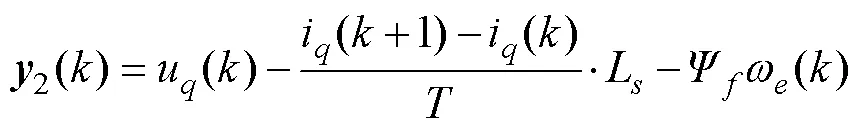
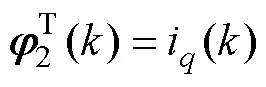
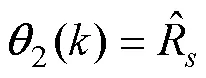
得到带遗忘因子的RLS辨识电机电感的递推公式

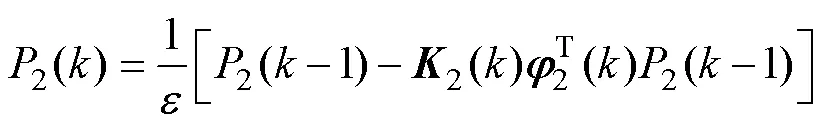

由该办法辨识得到电机的定子电阻和电感值。
3.3 基于带遗忘因子的RLS龙伯格观测器设计

4 仿真结果与分析
4.1 试验系统构建
文中设计的水下推进器无位置传感器控制系统采用双闭环和SVPWM控制,内环为电流环,采用i=0的控制方式,外环为转速环控制。控制系统结构如图4所示。
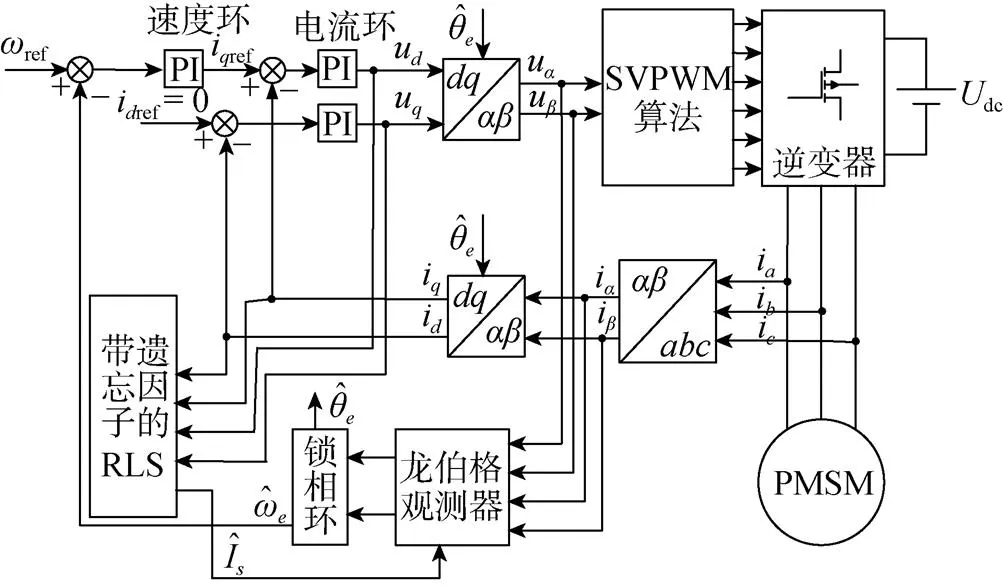
图4 水下推进器无位置传感器控制系统图

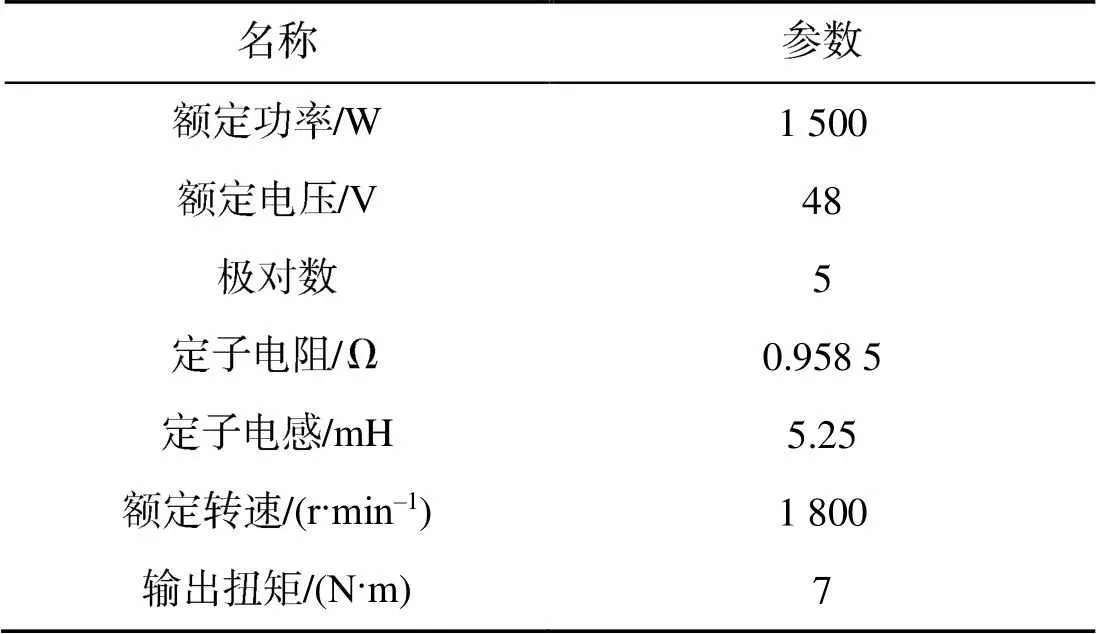
表1 PMSM参数
在整个系统建模过程中,最重要的是建立一个参数可变的电机模型,从而实现改变电机参数的作用。PMSM可变模型如图5所示。
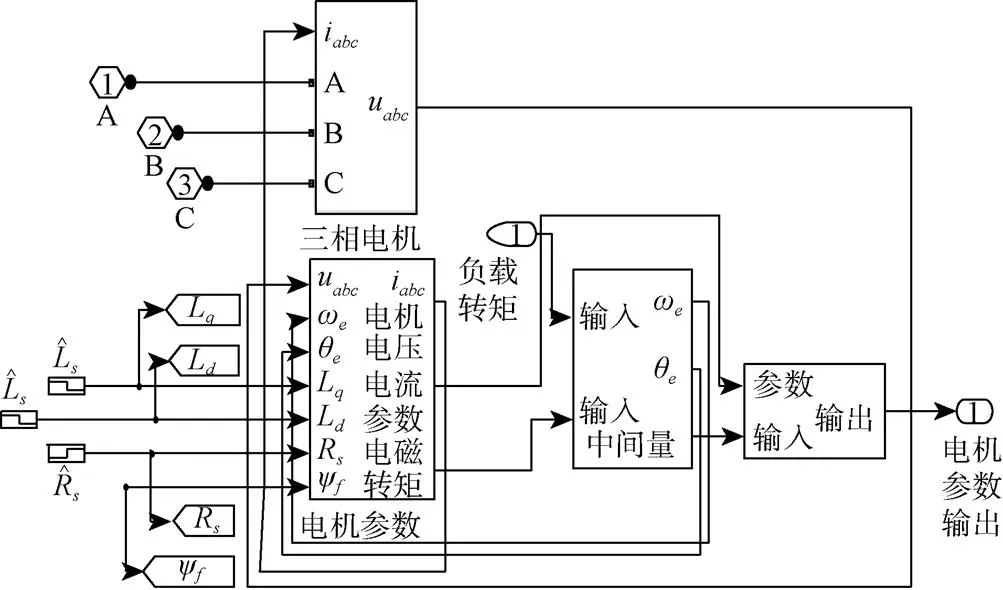
图5 PMSM参数可变模型
建立龙伯格观测器模型,电机的三相电流和电压作为输入,最终通过锁相环得到电机的转子位置和速度。龙伯格观测器模型如图6所示。
建立带遗忘因子的RLS龙伯格观测器模型,其模型如图7所示。其中带遗忘因子的RLS算法通过函数引入模型中。
最终得到带遗忘因子的RLS龙伯格观测器模型,如图8所示。
4.2 仿真结果分析
为了更加接近于真实工况,假设电机满载工作在1 500 r/min最大转速下,定子电阻会随着温升而变化。经实验结论可知,当温升变化25℃时,电阻参数变化约20%。由于水下推进器主要通过水散热,散热性能很好,而电感随着电流变大而减少。所以在0~0.2 s内,电机的定子电阻和定子电感都为初始值,即L=5.25 mH,R=0.952 5Ω;在=0.2 s时,电机仍然工作在最大转速下,电感阶跃减少约10%,变为L=4.725 mH,电阻阶跃增大约10%,变为R=1.047 75 Ω。图9为带遗忘因子的RLS辨识电机定子电感的估计值与实际值,图10为带遗忘因子的RLS辨识电机定子电阻的估计值与实际值。

图6 龙伯格观测器模型

图7 带遗忘因子的RLS模型
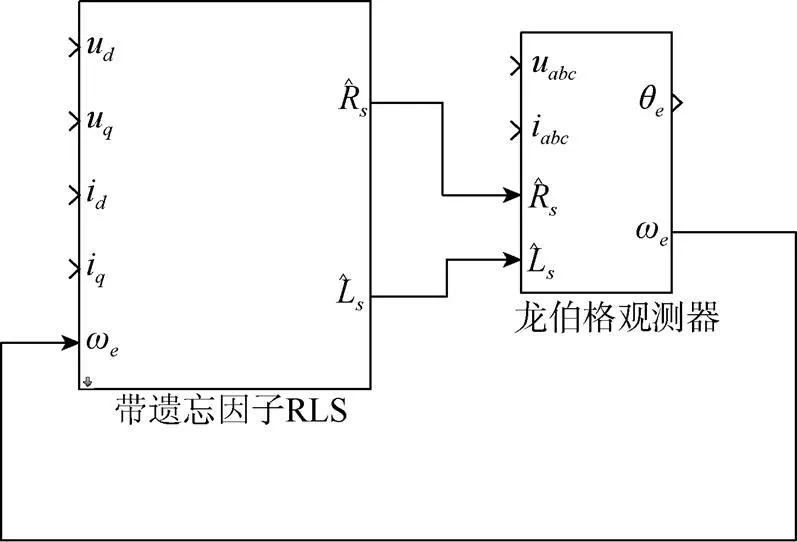
图8 带参数辨识的龙伯格观测器模型

图9 带遗忘因子的RLS辨识定子电感的估计值与实际值

图10 带遗忘因子的RLS辨识定子电阻的估计值与实际值
图11(a)和图12(a)为未结合参数辨识和结合参数辨识的龙伯格观测器观测得到的估算反电动势图,(b)为其局部放大图。
通过图11和图12可以看到,在=0.2 s时,电机定子电感和定子电阻发生阶跃突变,未结合参数辨识的龙伯格观测器,由于观测器模型仍然是电机参数的初始值,所以对电机反电动势的估算出现了较大的振荡; 而结合参数辨识的龙伯格观测器,对电机反电动势的估算出现振荡后很快便收敛稳定。
图13为龙伯格观测器观测得到的电机转子实际位置与估计位置误差图。
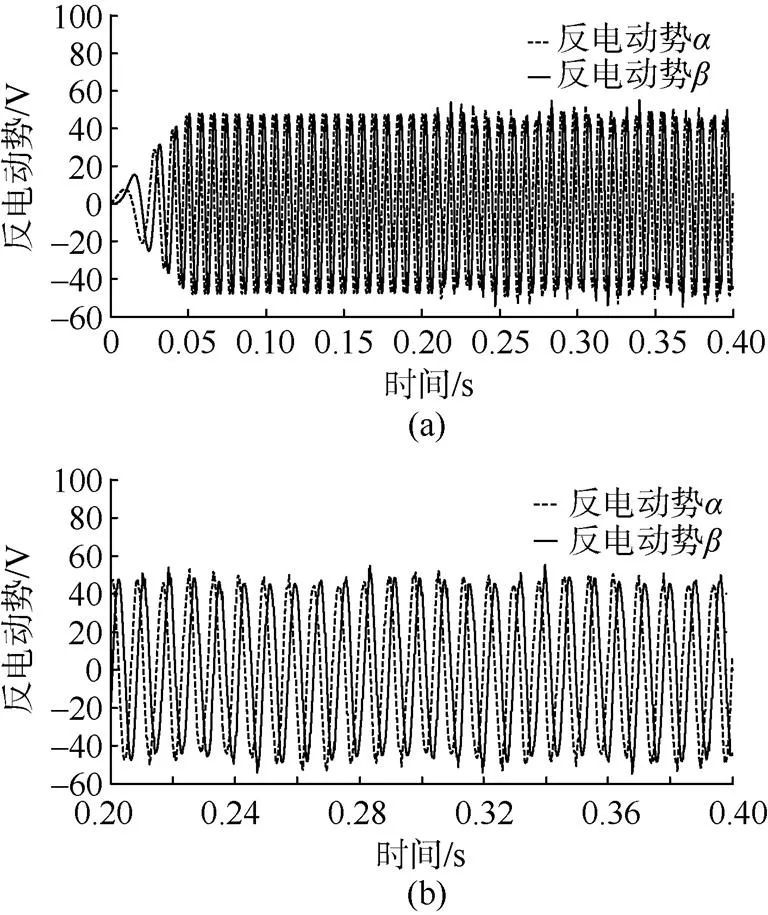
图11 未结合参数辨识的龙伯格观测器估算反电动势
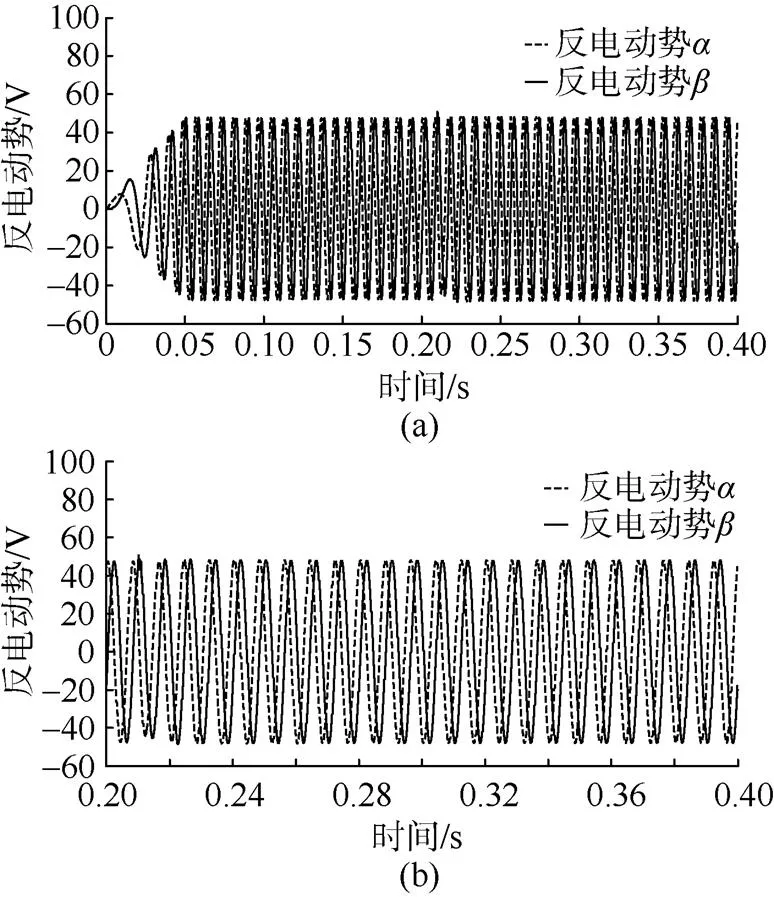
图12 结合参数辨识的龙伯格观测器估算反电动势

图13 龙伯格观测器转子位置误差
图14和图15为龙伯格观测器观测得到的转子实际转速和估计转速及其误差图。
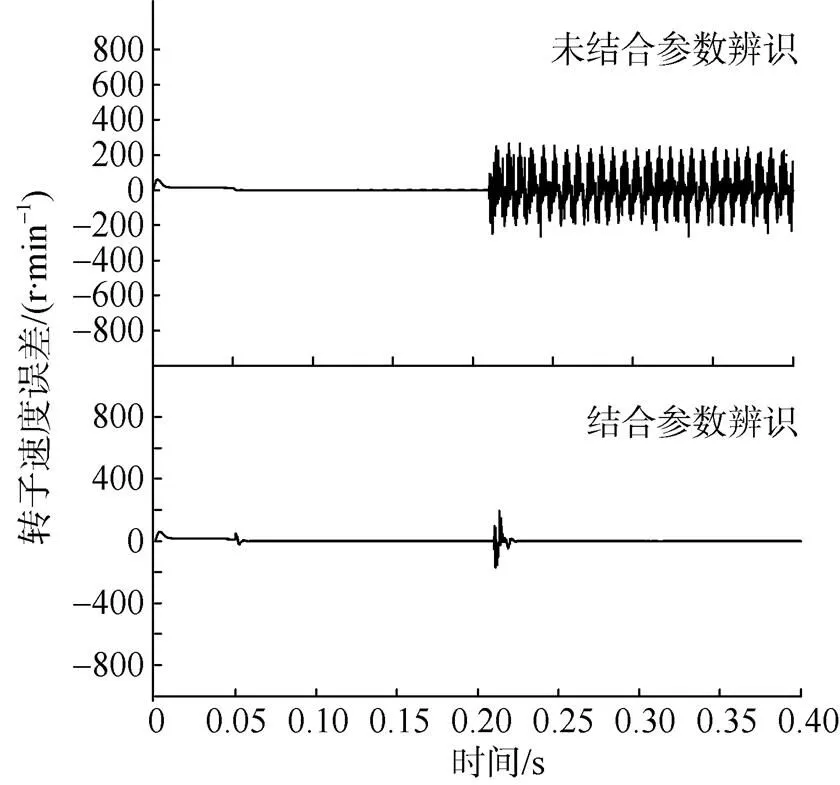
图15 龙伯格观测器转子实际转速与估计转速误差
通过图14和图15可以看出,在=0.2 s,未结合参数辨识的龙伯格观测器,由于自身的模型参数与电机的真实值不同,使得估算的电机反电动势不稳定,最终表现在转子转速出现了将近400 r/min的大幅度振荡; 而结合了参数辨识的龙伯格观测器,其模型参数接近于电机的真实值,所以表现在转子转速误差上出现波动后,很快收敛到正常误差范围。
5 结束语
为了实现水下推进器系统控制,解决电机定子电感和电阻参数在环境影响下的改变对无位置传感器控制性能的影响问题,文中通过基于参数辨识的龙伯格观测器,实现了水下推进器无位置传感器控制系统双闭环和SVPWM控制。
通过仿真结果可以得出,电机转速最终表现出较大振荡的根本原因在于,当电机定子电阻电感参数发生变化时,龙伯格观测器中的模型参数仍然为电机的初始参数,导致对反电动势的观测出现了较大误差; 通过结合带遗忘因子的RLS龙伯格观测器,降低了对电机参数的敏感性,得到了更稳定的转子位置和速度辨识值,为水下航行器的多自由度运动提供了保障。文中电机控制仅限于仿真,电机的定子电阻和电感在实际工况中的变化值还需结合实验得到变化曲线,后续工作可以此继续深入。
[1] 杨国良,李建雄. 永磁同步电机控制技术[M]. 北京: 知识产权出版社,2015.
[2] 刘伟,王俊. 永磁同步电机参数辨识研究综述[J]. 电气技术,2020,21(8): 1-5,135.
Liu Wei,Wang Jun. Summary of Research on Parameter Identification of Permanent Magnet Synchronous Motors[J]. Electrical Technology,2020,21(8): 1-5,135.
[3] 陈再发,刘彦呈,卢亨宇. 船舶推进永磁同步电机参数在线辨识方法研究[J]. 电机与控制应用,2018,45(10): 66-72.
Chen Zai-fa,Liu Yan-cheng,Lu Heng-yu. Research on On-line Identification Method of Marine Propulsion Permanent Magnet Synchronous Motor Parameters[J]. Electric Machines and Control Applications,2018,45(10): 66-72.
[4] 金宁治,周凯,Herbert Ho-Ching IU. 带有自适应参数辨识的IPMSM MTPA控制[J]. 电机与控制学报,2020,24(7): 90-101.
Jin Ning-zhi,Zhou Kai,Herbert Ho-Ching IU. IPMSM MTPA Control with Adaptive Parameter Identification[J]. Journal of Electrical Machines and Control,2020,24(7): 90-101.
[5] 刘细平,胡卫平,邹永玲,等. 改进粒子群算法的永磁同步电机多参数辨识[J]. 电机与控制学报,2020,24 (7):112-120.
Liu Xi-ping,Hu Wei-ping,Zou Yong-ling,et al. Multi-parameter Identification of Permanent Magnet Synchronous Motors Based on Improved Particle Swarm Optimization[J]. Journal of Electrical Machines and Control,2020,24(7): 112-120.
[6] 荆禄宗,吴钦木. 基于递归神经网络的永磁同步电机参数辨识研究[J]. 电气传动,2020,50(3): 87-91,101.
Jing Lu-zong,Wu Qin-mu. Research on Parameter Identification of Permanent Magnet Synchronous Motor Based on Recurrent Neural Network[J]. Electric Drive,2020,50(3): 87-91,101.
[7] 董召强,徐秋霞,高瑾. 基于最小二乘法和硬件在环平台的永磁同步电机参数辨识[J]. 电机与控制应用,2017,44(6): 57-62.
Dong Zhao-qiang,Xu Qiu-xia,Gao Jin. Permanent Magnet Synchronous Motor Parameter Identification Based on Least Squares Method and Hardware-in-the-loop Platform[J]. Electric Machines and Control Applications,2017,44(6): 57-62.
[8] Zhang G,Wang G,Xu D,et al. ADALINE-network-based PLL for Position Sensorless Interior Permanent Magnet Synchronous Motordrives[J]. IEEE Trans. Power Electron.,2016,31(2): 1450-1460.
[9] 郭志荣,高峰,王其林. 基于RBF网络和MRAS的鱼雷永磁同步电机无速度传感器控制方法[J]. 水下无人系统学报,2017,25(6): 448-452.
Guo Zhi-rong,Gao Feng,Wang Qi-lin. Speed Sensorless Control Method of Torpedo Permanent Magnet Synchronous Motor Based on RBF Network and MRAS[J]. Journal of Underwater Unmanned Systems,2017,25(6): 448-452.
[10] 谭人之.工业机器人永磁同步电机的参数辨识与控制研究[D]. 长沙: 湖南大学,2018.
[11] 陈光普. 基于自适应龙伯格观测器的永磁同步电机无位置传感器控制系统研究[D]. 杭州: 浙江大学,2019.
[12] 林瑶瑶. 永磁同步电机参数辨识方法与伺服控制技术研究[D]. 大连: 大连理工大学,2018.
[13] Dang D Q,Rafaq M S,Choi H H,et al. Online Parameter Estimation Technique for Adaptive Control Applications of Interior PM Synchronous Motor Drives[J]. IEEE Trans. Ind. Electron.,2016,63(3): 1438-1449.
[14] 刘永钦,沈艳霞,纪志成.基于改进型最小二乘法的感应电机转动惯量辨识[J].电机控制与应用,2008,35(12): 13-17.
Liu Yong-qin,Shen Yan-xia,Ji Zhi-cheng. Identification of Inertia Moment of Induction Motor Based on Improved Least Square Method[J]. Motor Control and Application,2008,35(12): 13-17.
[15] 钱鑫,王崇武,于琨琨,等. 基于递推最小二乘法的永磁同步电机参数辨识[J]. 鱼雷技术,2014,22(6): 452- 456.
Qian Xin,Wang Chong-wu,Yu Kun-kun,et al. Permanent Magnet Synchronous Motor Parameter Identification Based on Recursive Least Squares Method[J]. Torpedo Technology,2014,22(6): 452-456.
[16] 刘旭,王旭平,王淑红,等. 基于最小二乘法的永磁同步电机电感辨识研究[J]. 电机与控制应用,2020,47(6): 1-5,32.
Liu Xu,Wang Xu-ping,Wang Shu-hong,et al. Research on the Inductance Identification of Permanent Magnet Synchronous Motor Based on Least Square Method[J]. Electric Machines and Control Applications,2020,47(6): 1-5,32.
1. 戴磊,李洋洋,尤钱亮,等. 基于LMI算法的永磁同步电机混沌最优控制. 2021,29(3).
2. 张国楠,胡利民,王建平,等.一种低速大扭矩永磁同步电机设计方案. 2020,28(6).
3. 徐鹏程,曾庆军,陈尧伟,等. 基于导管螺旋桨负载的ROV推进器滑模控制. 2020,28(5).
4. 尤钱亮,魏海峰,常徐,等. 基于三自由度动态内模解耦的PMSM弱磁控制. 2020,28(1).
5. 张明明,刘维亭,魏海峰,等. 基于滑模观测器的PMSM单相霍尔位置传感器故障容错控制算法. 2019,27(6).
6. 郭志荣,高峰,王其林. 基于RBF网络和MRAS的鱼雷永磁同步电机无速度传感器控制方法. 2017,25(6).
Sensorless Control of Underwater Propulsion PMSM Based on Parameter Identification
1,1,1,1,1,2
(1. Electronic and Information College,Jiangsu University of Science and Technology,Zhenjiang 212003,China; 2. Marine Equipment Research Institute,Jiangsu University of Science and Technology,Zhenjiang 212003,China)
In the operation of an underwater propeller,parameters of the permanent magnet synchronous motor(PMSM),such as stator resistance and inductance,are changed based on the temperature and current,resulting in a large error of the rotor position and speed,which are estimated by a sensorless control algorithm. In this paper,a sensorless control method is proposed to control an underwater propeller based on the Luenberger observer combined with parameter identification. In this method,based on a double closed-loop vector control strategy,recurrence least square(RLS) combined with a forgetting factor is adopted as an online parameter identification algorithm to evaluate the stator resistance and motor inductance. The initial resistance and inductance parameters in the Luenberger observer model are thereafter replaced using the same algorithm. The back electromotive force estimated through the Luenberger observer is used as the input of the phase-locked loop. Finally,the position and speed of the rotor are obtained from the output of the phase-locked loop. The simulation results show that the rotor position and speed can be rapidly and accurately identified by Luenberger observer when this parameter identification technique,which reduces the sensitivity of motor parameters on sensorless control system,is used.
underwater propeller; permanent magnet synchronous motor; Luenberger observer; parameter identification; recurrence least square; sensitivity
TM351; TJ630.32
A
2096-3920(2021)04-0442-09
10.11993/j.issn.2096-3920.2021.04.011
陈尧伟,曾庆军,戴晓强,等. 基于参数辨识的水下推进永磁同步电机无位置传感器控制[J]. 水下无人系统学报,2021,29(4): 442-450.
2020-10-22;
2020-11-20.
国家自然科学基金项目(11574120); 江苏省产业前瞻与共性关键技术项目(BE2018103).
陈尧伟(1996-),男,在读硕士,主要研究方向为电力电子装置与系统.
(责任编辑: 许 妍)

