中美欧日规范独立基础冲剪计算对比研究
孔子昂 徐秀凤 任传尧 贾海涛 王正云 周 强 黄永春
(1.浙江绿城建筑设计有限公司青岛分公司,青岛 266071;2.青岛黄海学院建筑工程学院,青岛 266427;3.青岛杰地建筑设计有限公司,青岛 266071)
0 引言
柱下独立基础的冲切破坏和剪切破坏都是比较危险的脆性破坏,但两者的受力机理不一样,冲切破坏是在集中反力作用下,在板内产生正应力和剪应力,在柱头四周形成较大的主拉应力,导致沿柱头四周出现斜裂缝,并向下扩展形成破坏锥体;剪切破坏类似于单向板和梁斜截面破坏。另外,两者的破坏形式也不一样,剪切破坏具有平面特征,破坏面为贯穿整个构件的平面;而冲切破坏呈现空间特征,基础在集中力作用区域发生与其他区域相互脱离的现象,脱离体一般呈截头锥体。
为避免柱下独立基础发生冲切和剪切破坏,各国规范均要求验算冲切、剪切承载力,但验算方法不尽相同。本文对中国、美国、欧洲和日本四个世界上主要国家和地区的相关规定进行了总结,从基础验算条件、控制截面位置、承载力验算公式以及冲切锥底面的形状等方面对比了各国规范的异同。并选取了8个轴心受压的独立基础试验,通过各国规范计算得到的轴力设计值与试验值的比较,进一步分析了各国规范在计算结果上的差异。最后采用MSC.Marc有限元软件在已有试验的基础上对纵筋配筋率对基础冲切、剪切承载力的影响进行了分析。
1 基础验算条件
《建筑地基基础设计规范》(简称GB 50007)[1]将独立基础的验算分为两种情况,其验算判别条件见表1。
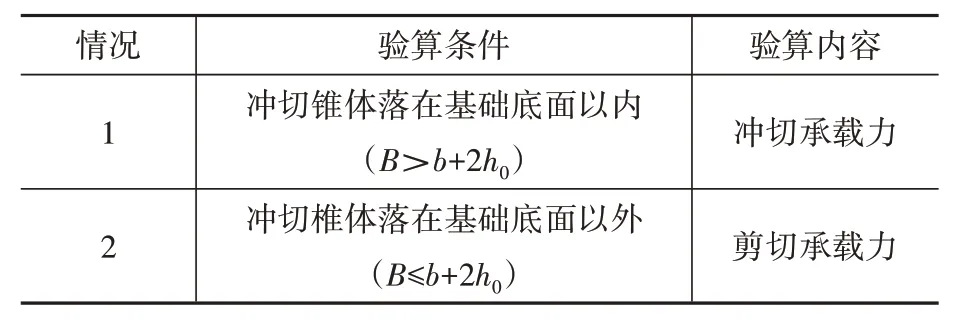
表1 基础验算条件Table 1 The check conditions of bases
美国规范ACI318-19[2]、欧洲混凝土规范Eurocode2[3](简称EU2)及日本混凝土结构标准技术规范[4](简称JGC15)规定:基础的抗剪承载力由单向受力的梁模式与双向受力的板模式中较严格的条件所控制。梁模式和板模式的验算方法分别类似于GB 50007中受剪切和受冲切承载力验算。
国内外规范的一个显著的不同是,国外规范板模式采用的是“整体破坏模式”,即其破坏面围绕柱子在空间上形成截头圆锥或棱锥体;而中国规范在冲切承载力验算时采用的是“局部破坏模式”,验算的是冲切锥最不利侧斜截面的冲切承载力。另外,JGC15指出由于独立基础的受力行为接近于深梁,在剪切验算时,当地基反力的合力中心距离支座表面的距离a与基础有效高度d之比小于2时,应采用剪压承载力作为基础的受剪承载力;当a/d≥2时,应采用线性构件的受剪承载力作为基础的受剪承载力。
2 剪切和冲切验算控制截面
各国规范均规定应在支座表面及变阶处进行剪切及冲切承载力验算,但控制截面选取的位置各有不同,如表2所示。
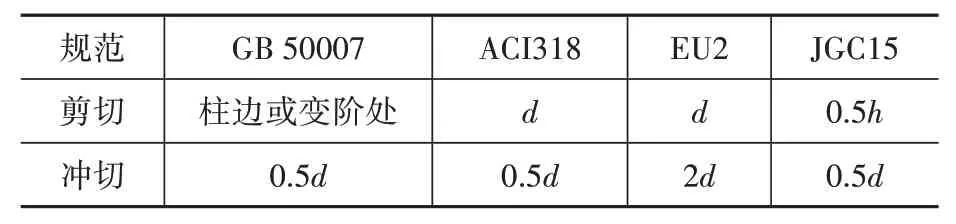
表2 控制截面距离柱边或变阶处的距离Table 2 The distance between control section and column edge or change steps
从表2可知,仅中国规范将剪切控制截面取在柱边或变阶处,这意味着在抗剪验算时,中国规范具有最大的受荷面积。在冲切方面,欧洲规范的冲切破坏角最小,因此其冲切面位置距柱边最远。
3 承载力验算公式
3.1 中国规范
GB 50007中基础剪切承载力验算公式为
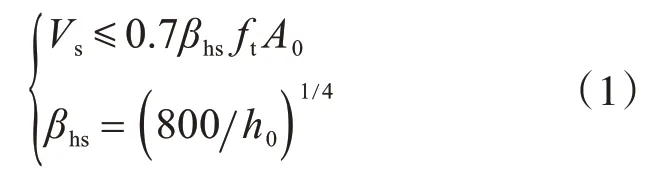
式中:Vs为剪力设计值;ft为混凝土轴心抗拉强度设计值;βhs为截面高度影响系数;A0为验算截面处的有效截面面积;h0为基础有效高度。
基础冲切承载力验算公式为
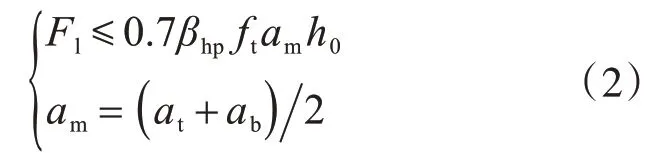
式中:Fl为冲切力设计值;βhp为截面高度影响系数;am为冲切破坏锥体最不利一侧计算长度;at和ab分别为冲切破坏锥体最不利一侧斜截面的上边长和下边长。
3.2 美国规范
ACI318-19规定,基础的抗剪承载力为
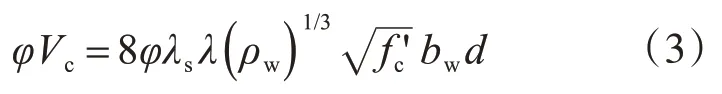
且Vc应满足:
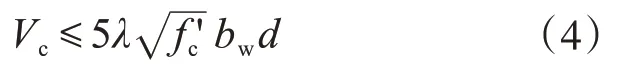
式中:λ为考虑轻骨料混凝土强度折减系数,对于普通混凝土取1.0;f'c为圆柱体强度特征值,单位为psi;bw和d分别为基础宽度和有效高度,单位为in;φ为强度折减系数,取0.75;ρw=As/dbw,As为受压区边缘以上基础总高度2/3范围内穿过关键截面的纵向钢筋的总和;λs为尺寸效应修正系数,按式(5)计算,在独立基础设计时,可取1。
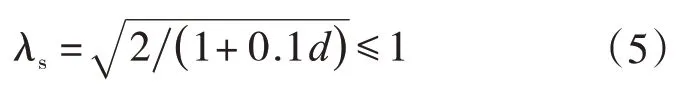
ACI318-11[5]中剪切承载力的计算公式为。对比可知,新版规范增加了尺寸效应和配筋率的影响,当配筋率ρ>1.65%时ACI318-19计算结果较大,否则ACI318-11计算结果较大。
基础的冲切承载力按式(6)计算:
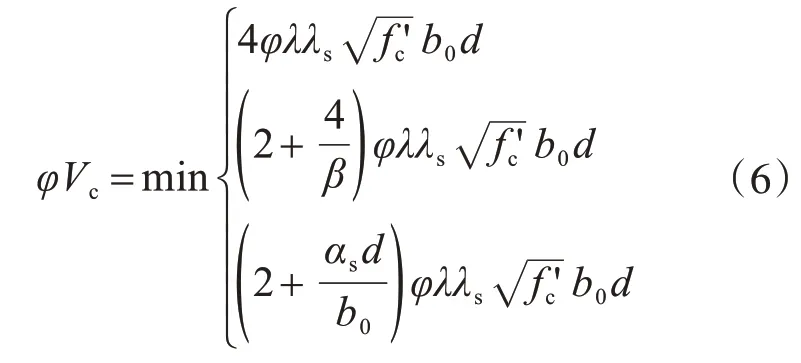
式中:d取两个方向的基础平均高度;b0为临界截面周长;β为柱截面长边与短边之比,对于非矩形加载面,其定义为有效加载面内的最长尺寸与垂直方向的最长尺寸之比;αs为柱位置系数,内柱、边柱和角柱分别取40、30和20。与ACI318-11相比,ACI318-19增加了尺寸效应的影响。
当基础和柱之间需要通过剪应力来传递不平衡弯矩时,计算得到的最大剪应力设计值不应超过沿临界周长的平均剪应力φVc/b0d。除ACI318-19规定的不平衡弯矩分配系数在满足一定条件时可进一步调整外,最大剪应力的计算方法与GB 50007第8.4.7-1条及附录P中规定的内容完全相同。
3.3 欧洲规范
EU2中基础的抗剪承载力按下式计算:
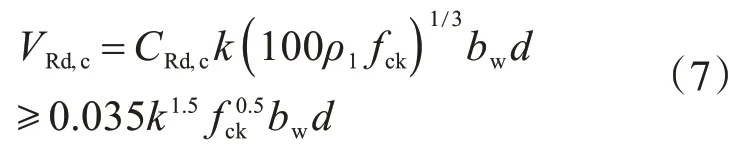
式中:bw为基础宽度;ρ1为受拉纵筋配筋率,ρ1≤0.02;系数≤2.0;CRd,c取0.18/γc,γc为材料分项系数,取1.5;fck为混凝土圆柱体抗压强度标准值。
同时,EU2还规定,可以将距离支座较近的荷载对剪力设计值的贡献进行折减,即距离支座边在0.5d≤av≤2d之间的荷载,其对于控制截面处剪力的贡献可以乘以折减系数av/2d,对于av≤0.5d的情况,取av=0.5d。
验算基础冲切时,EU2按下式进行设计:

式中,νEd和νRd,c分别为所选控制截面处的冲切剪应力设计值和抗冲切剪应力设计值。
基本控制面处的抗冲切剪应力由下式确定:
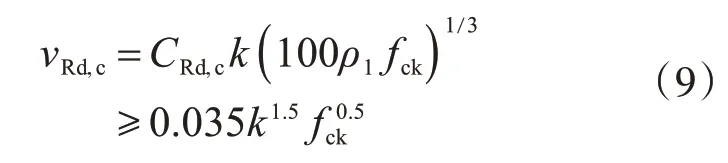
基本控制面以内的控制截面,其抗冲切应力由下式决定:
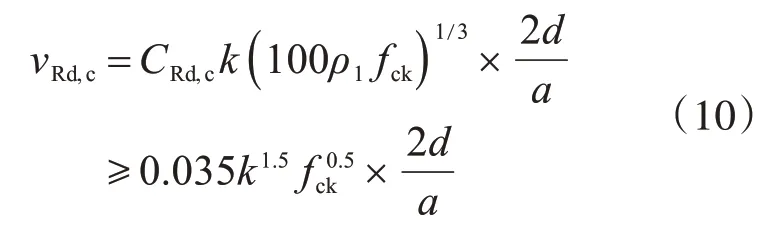
式中:a为控制截面到柱边的距离;ρ1取两个方向柱宽加每侧3d范围内的截面纵向受拉钢筋配筋率乘积的平方根,且小于或等于0.02;d为两个方向柱边的平均有效高度。
νEd由下式决定:
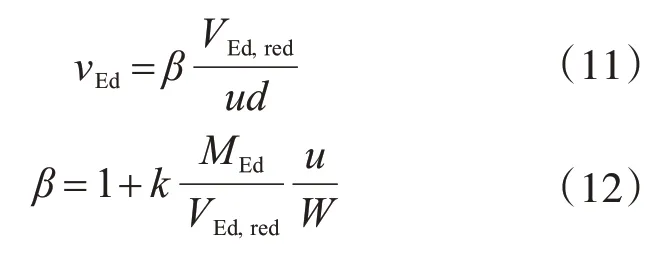
式中:VEd,red为扣除控制周长内反力后的基底净反力之和;MEd为控制截面传递的不平衡弯矩;u为所选控制截面的周长;W为对应于控制截面的几何常量;k为通过剪应力传递不平衡弯矩的分配系数,可按表3进行取值。

表3 矩形柱的k值Table 3 The k for the rectangular column
对于矩形内柱,基本控制面处的W可按下式计算:
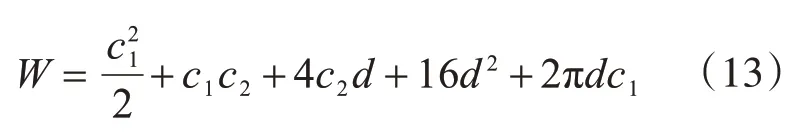
式中,c1和c2分别为垂直和平行于弯矩方向的柱子边长。
对于矩形内柱,可采用下式近似计算β:
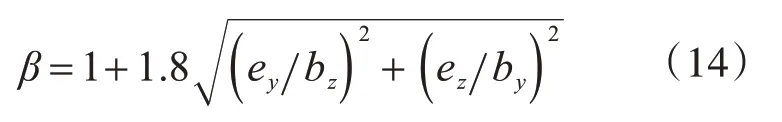
式中,by和bz分别为控制截面边长;ey和ez分别为对应的偏心距。
3.4 日本规范
当a/d≥2时,基础的剪切承载力为
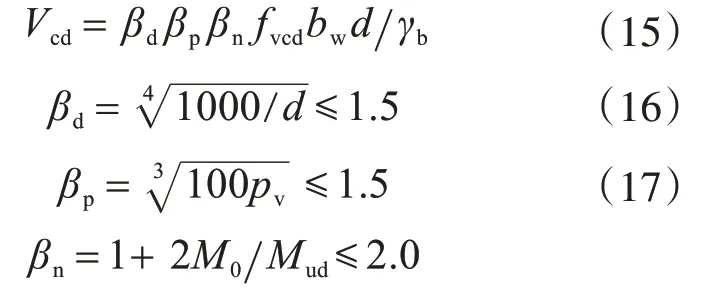
或
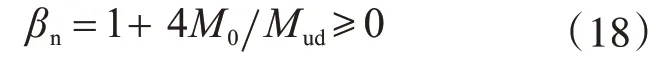
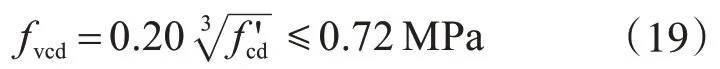
式中:fcd′为混凝土抗压强度设计值,其值等于fck′/1.3,fck′为圆柱体抗压强度标准值;bw为基础宽度;d为柱根处的基础有效高度;pv为纵向受拉钢筋配筋率;γb为构件因子,取1.3;M0为在实际轴压作用下使受拉区边缘应力为零的弯矩,对于独基一般有M0=0,Mud为纯弯状态下截面的抗弯承载力。
当a/d<2时,基础的剪压承载力为
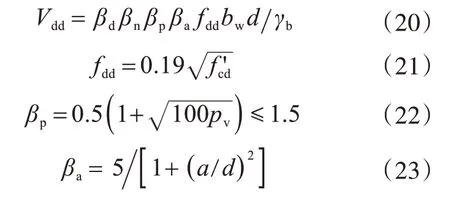
当支座远离基础自由边且无弯矩时,独基的冲切承载力为
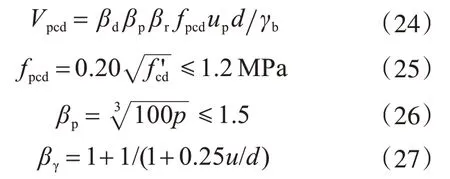
式中:p为两个方向受拉钢筋配筋率的平均值;u为有效加载面的周长;up为临界截面周长。
当基础受到弯矩和扭矩作用时,应将抗冲切承载力乘以系数1/α,α为
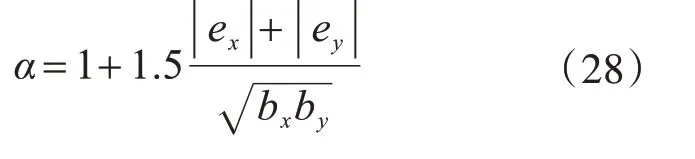
式中:ex,ey分别为x方向和y方向的偏心距;bx,by分别为临界截面x方向和y方向的边长。
4 承载力验算公式对比
4.1 冲切锥底面的形状
GB50007、ACI318-19、EU2及JGC15中规定的冲切锥底面如图1-图4所示。对比可知,中、美、日规范冲切锥底面距离有效加载面的距离均为d,而欧洲规范中为2d,这导致其冲切锥斜截面与基础底面的夹角θ不再是45°,而是26.6°,如图5所示。同时,根据EU2的规定,当阶形基础的阶宽高比小于2或锥形基础的坡角大于26.6°时,无须进行冲切承载力验算。因此,某些根据我国规范需要验算冲切的基础,根据EU2的规定不再需要验算。除此之外,中、美规范在冲切锥底面角点处采用棱角,EU2和日本规范采用圆角,前者可以简化设计过程,同时也更容易配置抗冲切钢筋,后者则更符合试验的破坏形态。
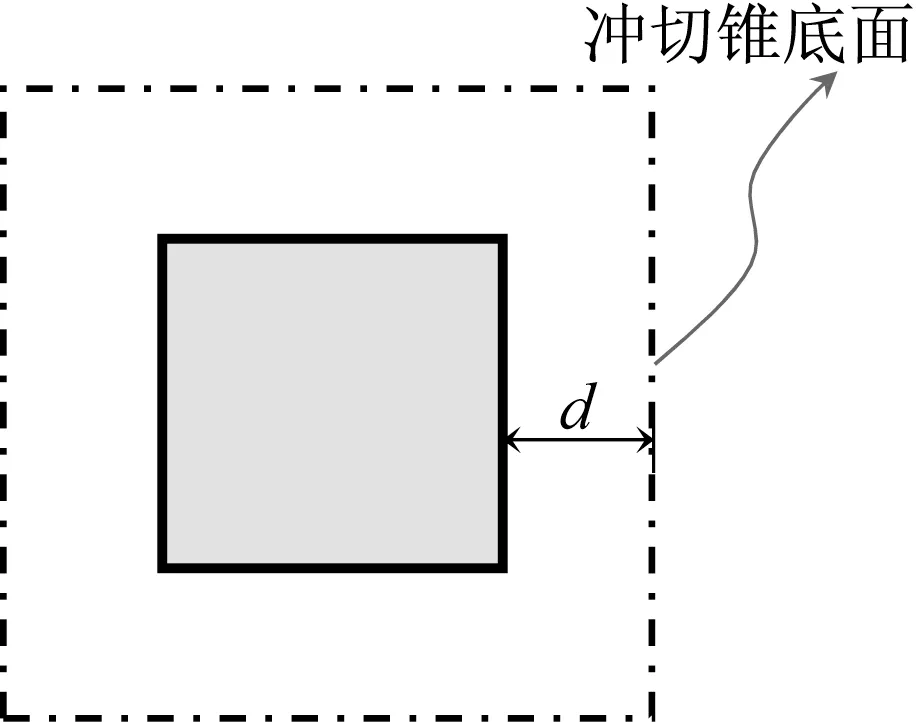
图1 GB 50007规定的冲切锥底面形状Fig.1 The bottom shape of punching cone in GB 50007
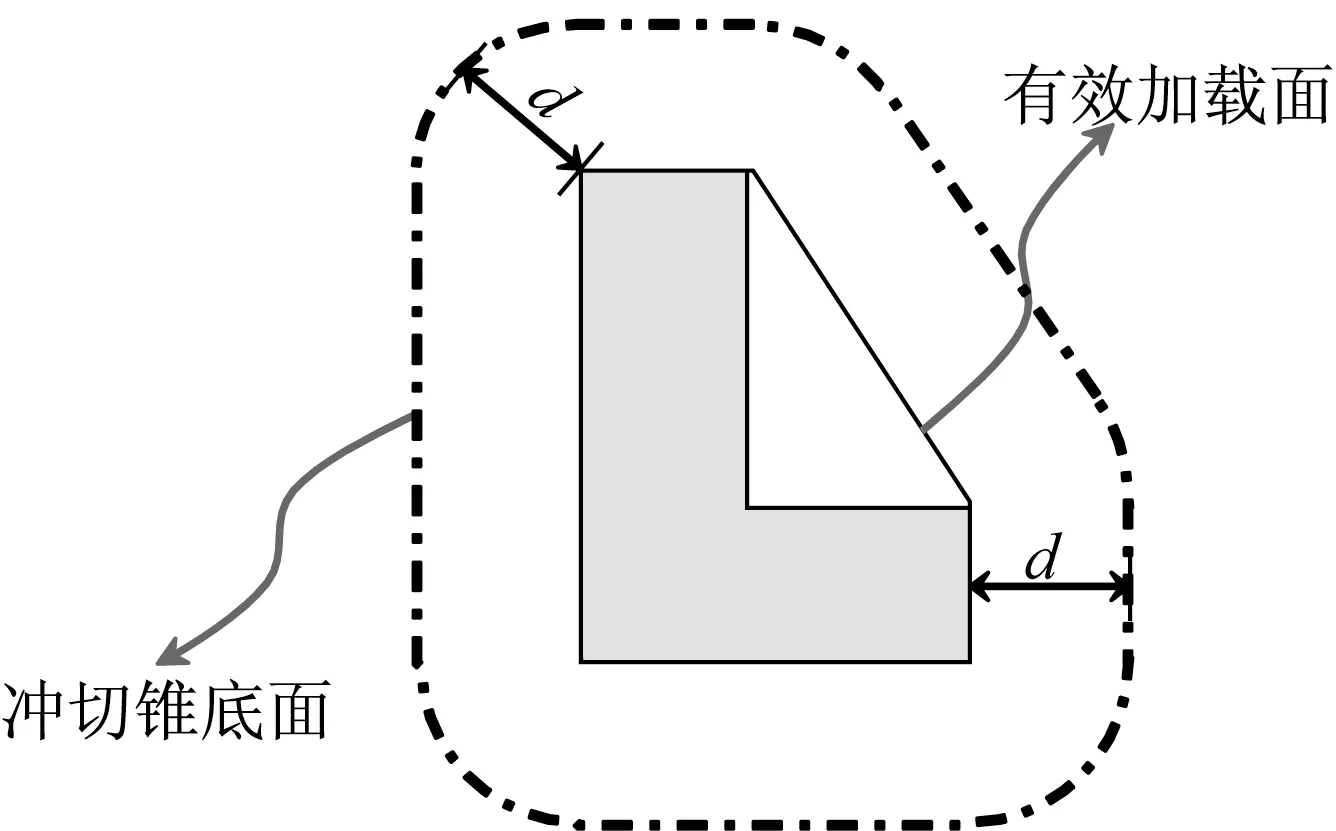
图4 JGC15定义的冲切锥底面形状Fig.4 The bottom shape of punching cone in JGC15
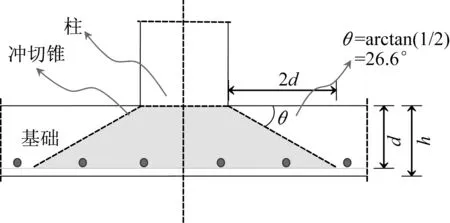
图5 EU2定义的冲切锥Fig.5 The punching cone defined by EU2
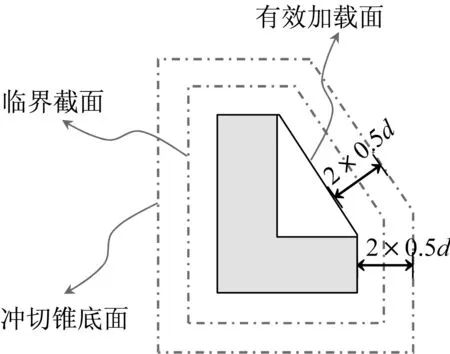
图2 ACI318-19规定的冲切锥底面Fig.2 The bottom shape of punching cone in ACI318-19
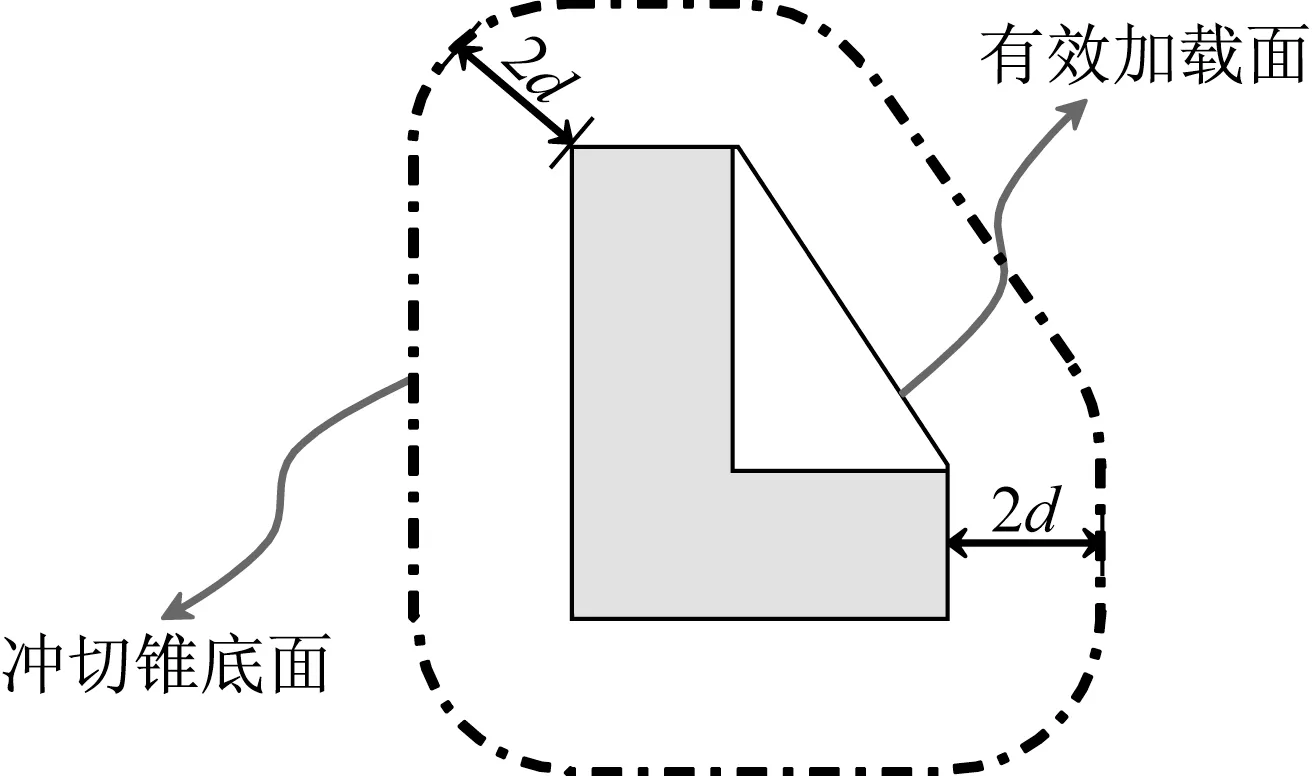
图3 EU2规定的冲切锥底面的形状Fig.3 The bottom shape of punching cone in EU2
4.2 影响参数对比
各国规范在剪切、冲切承载力计算时均考虑了混凝土强度的影响,但各公式中对混凝土强度的定义不尽相同,中国规范采用混凝土轴心抗拉强度设计值ft,该值由150 mm立方体抗压强度标准值考虑混凝土实体强度与立方体试件强度的差异、棱柱体强度与立方体强度之比、混凝土的脆性折减系数和材料分项系数换算得到[6],美、欧、日规范采用的是直径6英寸(152 mm)、高12英寸(305 mm)的圆柱体的抗压强度fc′(ACI、EU2和JGC15分别对应于符号fc′、fck和fck′),对于C60以下的混凝土,圆柱体抗压强度fc′和立方体抗压强度标准值fcu,k之间的关系为fc′=0.79fcu,k[7]。由于美国规范和中国规范的混凝土材料保证率不一样,所以美国的fc′=0.79fcu,k是近似计算结果,其精确计算结果参见文献[8]。ACI318-19中没有材料强度“设计值”的概念,在设计时直接采用材料特征值fc′,同时引入了考虑多种因素的强度折减系数φ;EU2、JGC15和GB 50007则均在计算公式中直接或间接地考虑了材料分项系数。各国C20~C50混凝土材料特征值与我国混凝土强度等级的对应关系见表4。

表4 各国规范混凝土强度对应关系Table 4 The concrete strength conversion relation of each country standardizes N/mm2
在剪切承载力计算时,我国规范考虑了基础有效高度、基础宽度及截面高度影响系数三个参数;除以上参数外,美国、日本和欧洲规范均考虑了受拉纵筋配筋率的影响,另外,ACI318-19指出允许不考虑由基础高度变化引起的尺寸效应的影响,EU2允许对离支座较近范围内的外力对剪力的贡献进行折减,JGC15根据上述比值a/d,将承载力分为两种情况进行计算,在按深梁计算时,考虑参数a/d的影响。
在计算冲切承载力时,我国规范冲切影响因素与剪切一致,与我国规范相比,美国规范还考虑了临界截面周长、加载面尺寸、柱的位置、尺寸效应四个参数,其中尺寸效应的影响允许忽略;欧洲规范考虑了纵筋配筋率和尺寸效应的影响,对于位于基本控制截面以内的控制截面,可考虑承载力放大系数2d/a;日本规范考虑了纵向钢筋配筋率、加载面周长和尺寸效应等三个参数;另外,当基础通过剪应力传递不平衡弯矩时,美国和欧洲规范通过系数β考虑不平衡弯矩的影响,日本规范通过α对冲切承载力进行折减。
5 算例分析
为进一步分析各国规范的异同,选取了文献[9]中8个轴心受压柱下独立基础试验,基础高220 mm,保护层厚度为20 mm,柱截面尺寸均为250 mm×250 mm,基础长度均为1 450 mm。试验表明,JC3、JC4、JC7、JC8发生冲切破坏,JC1、JC2、JC5、JC6发生剪切破坏。通过基础承载力设计值与外力相等的条件,可以反算得到对应的轴力设计值,将其与试验值进行对比,如表5所示。
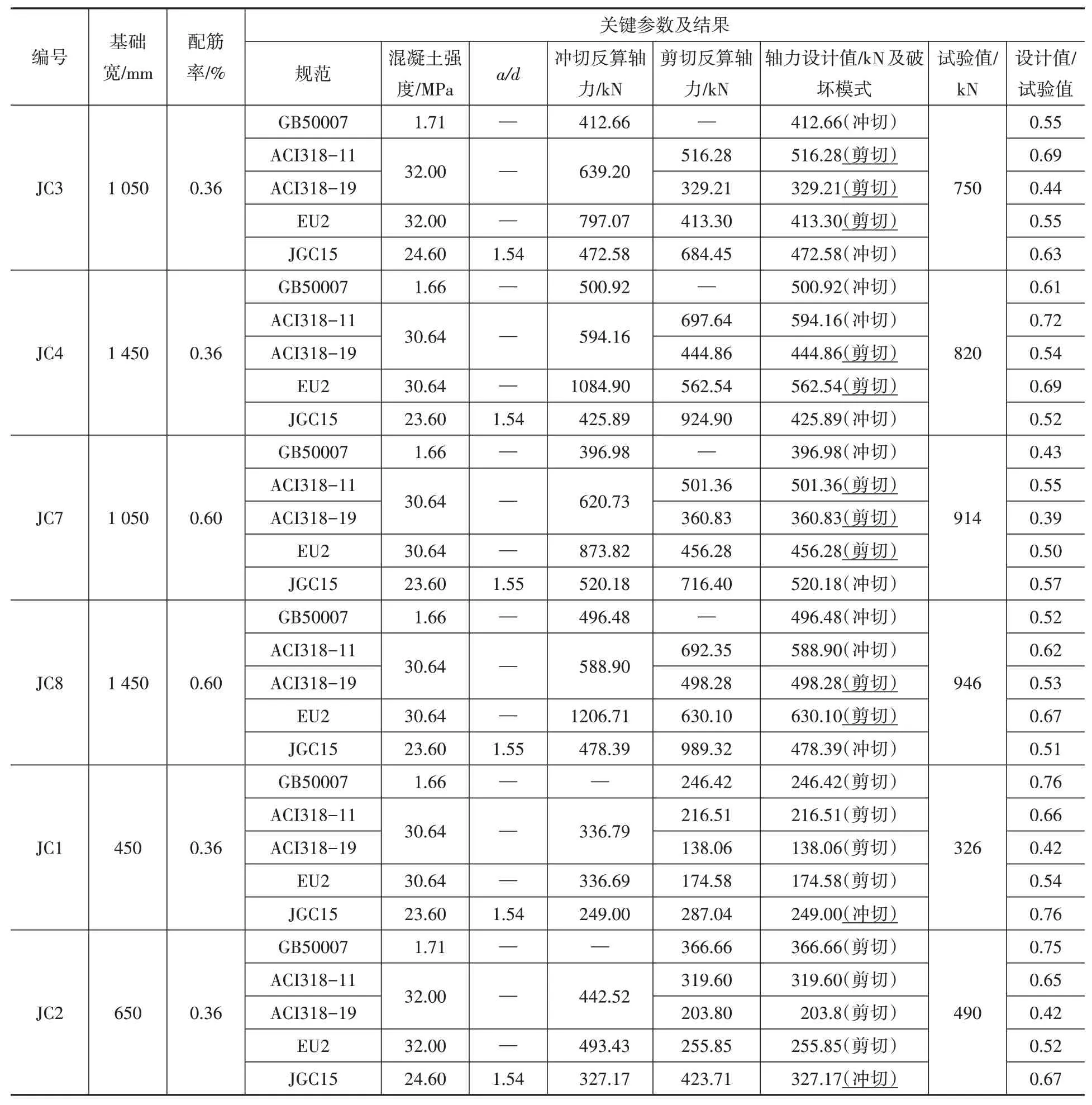
表5 轴力设计值与试验值之比Table 5 Ratio of axial force design value to test value
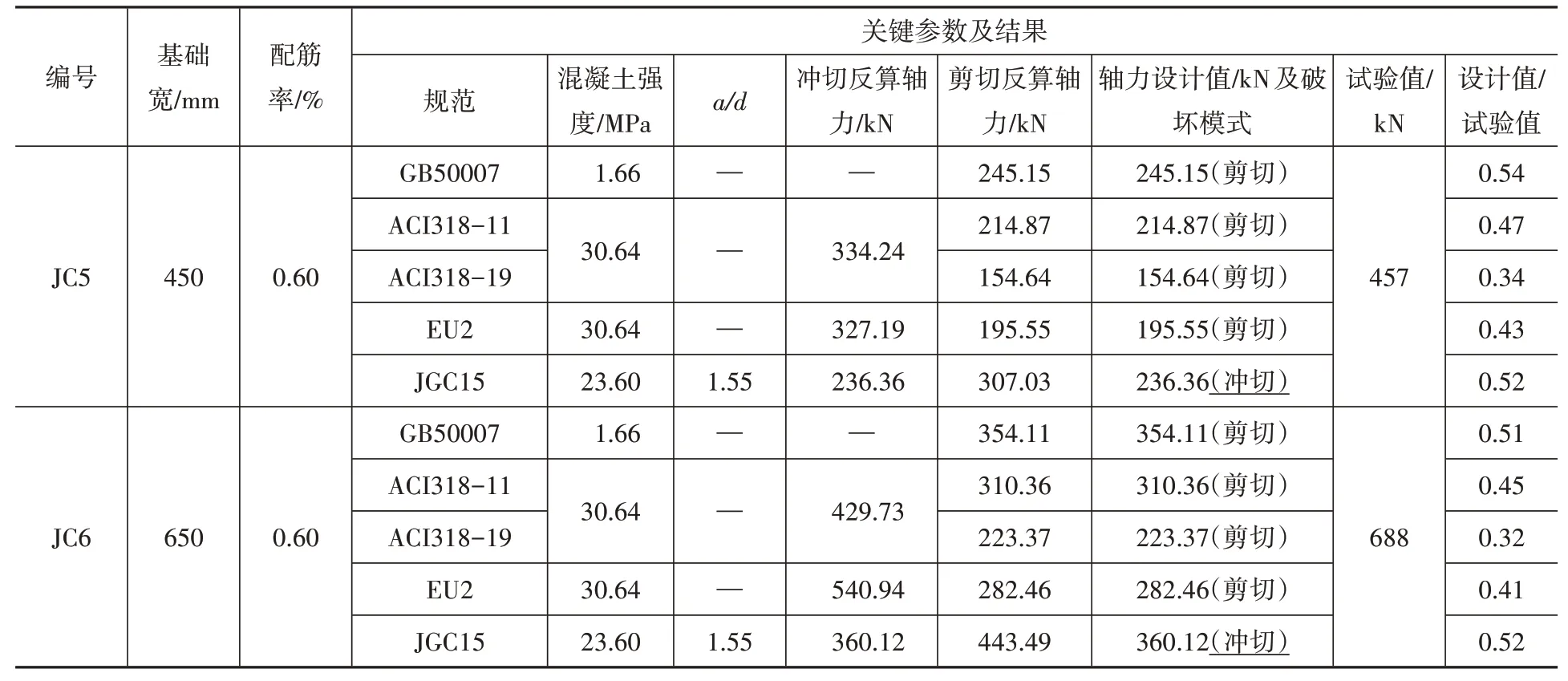
续表
从表5可知,各国规范计算得到的轴力设计值与试验值之比(简称轴力比)在0.32~0.76,各国规范均较为保守,其中ACI-19的计算结果最为保守,这是由于其在剪切计算时引入了配筋率的影响,计算表明,在配筋率小于1.65%时,其计算结果均小于ACI-11,由于本文选取的试验基础配筋率为0.36%和0.6%,均较小,使得ACI-19的计算结果最为保守;对于同一基础,按不同规范验算得到的破坏模式不尽相同,其中ACI-19均由剪切承载力控制,由于EU2定义的冲切锥角较小,导致按欧洲规范设计时均由剪切承载力控制,同时由于a/d<2,按JGC15计算的受剪承载力总是由剪压承载力控制,导致设计值由冲切承载力控制,而中国规范控制验算模式与实际破坏情况吻合最好;通过JC3与JC7、JC4与JC8、JC1与JC5、JC2与JC6的对比可知,美国规范ACI318-19、欧洲规范和日本规范虽然考虑了纵筋配筋率的影响,配筋率提高时设计值有所增加,但轴力比反而减小,说明规范对纵筋的有利影响考虑的不够充分。
6 配筋率对承载力的影响
6.1 数值模拟
由于中国规范在冲切、剪切承载力验算时未考虑纵筋配筋率的影响,而美国、欧洲、日本规范虽考虑了纵筋影响,但考虑的不够充分,因此本文以文献[9]中的矩形柱下扩展基础剪切试验JC2(配筋率0.36%)、JC6(配筋率0.6%),冲切试验JC3(配筋率0.36%)、JC7(配筋率0.6%)为研究对象,采用MSC.Marc有限元软件对其进行数值模拟及改变配筋率的参数分析。建模时混凝土结构为实体单元,钢筋为Truss单元,模型的尺寸及配筋情况与试验保持一致,钢筋和混凝土之间的黏结运用Links功能实现。混凝土受压本构采用E.Hognestad[10]本构模型,受拉段通过定义开裂应力、软化模量来模拟,当混凝土开裂后考虑裂缝面咬合作用,混凝土只能传递部分剪力,因此通过剪力传递系数对剪切模量进行折减,剪力传递系数的取值范围从0到1,0表示不传递剪力,1表示完全传递剪力,对于普通钢筋混凝土梁,该系数可取0.5,钢筋混凝土深梁取0.25,而对于剪切行为明显的剪力墙可取0.125[11],本文模型中剪力系数取0.25,混凝土屈服准则采用Buyukozuturk准则。钢筋采用双线性本构模型[11],采用Von Mises屈服准则,具体建模过程见文献[12],有限元模型如图6所示。
图6 有限元模型图Fig.6 The finite element model
6.2 模拟结果与试验结果的对比
数值模拟及试验得到的荷载-挠度曲线对比如图7所示。从图7可知当模拟荷载增加至528 kN、650 kN、733 kN和948 kN时JC2、JC6、JC3和JC7的曲线出现明显拐点,代表基础已经发生破坏,这与试验得到的JC2、JC6分别加载至490 kN和688 kN发生剪切破坏及JC3、JC7加载至750 kN和914 kN发生冲切破坏[9]较为接近。图8-图11分别为JC2、JC6、JC3和JC7最终破坏形态的对比,可知数值模拟得到的基础最终破坏形态与试验结果基本一致,因此可以此数值模型为基础对其进行改变配筋率的参数分析。
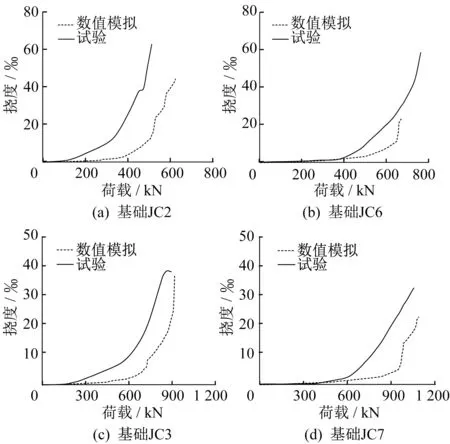
图7 数值模拟与试验荷载-挠度曲线对比Fig.7 Comparison between numerical simulation and test load-deflection curves
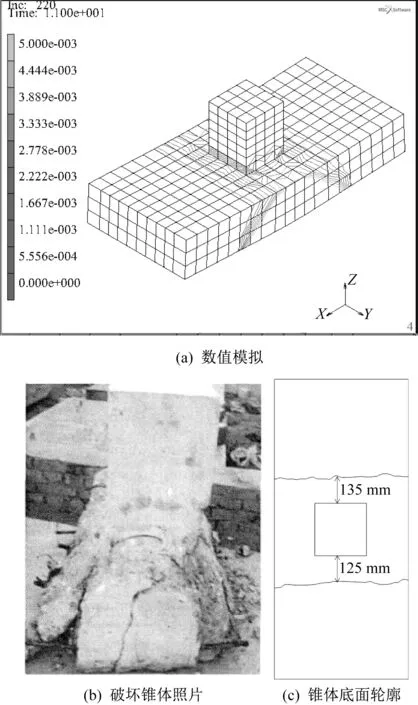
图8 数值模拟和试验得到的基础JC2剪切破坏对比Fig.8 Comparison of shear failure between numerical simulation and experiment of JC2
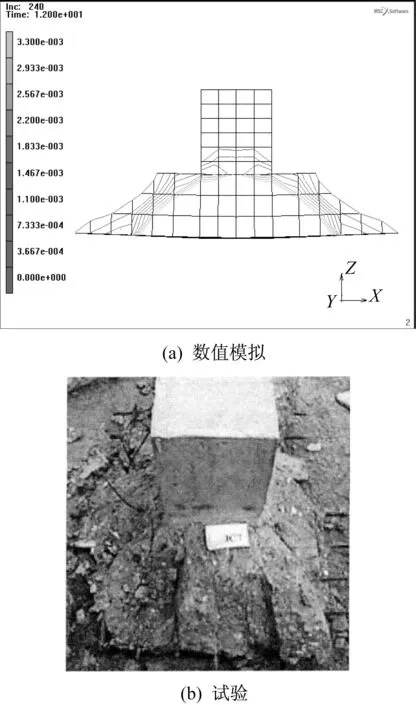
图11 数值模拟和试验得到的基础JC7冲切破坏对比Fig.11 Comparison of punching failure between numerical simulation and experiment of JC7
6.3 参数分析
在数值模型其他参数不变的情况下将基础的配筋调整为φ10@200、φ10@150和φ14@100,所对应的配筋率分别为0.18%、0.25%和0.82%,以考察基础配筋率对剪切和冲切承载力的影响。此三种模型计算得到的荷载-挠度曲线与配筋率为0.36%及0.60%的基础模型的对比情况如图12所示。从图12可知,配筋率增加时基础的剪切、冲切承载力均有所提高,但由于数值模拟基础底面的加载模式采用的是文献[9]实测得到的基底压力,当配筋率增加至0.82%时,基础未发生破坏,因此未得到配筋率大于或等于0.82%时的完整模拟结果。表6给出了不同配筋率的基础剪切和冲切承载力,配筋率为0.25%、0.36%、0.6%时的剪切承载力分别是配筋率为0.18%的基础的1.14倍、1.36倍、1.71倍,配筋率为0.25%、0.36%、0.6%时的冲切承载力分别是配筋率为0.18%的基础的1.25倍、1.43倍、1.88倍。承载力的提高倍数与配筋率的关系如图13所示,从图12可知,配筋率每增加0.2%剪切承载力提高0.334倍,冲切承载力提高0.4倍,配筋率对冲切承载力的贡献略大于剪切承载力。
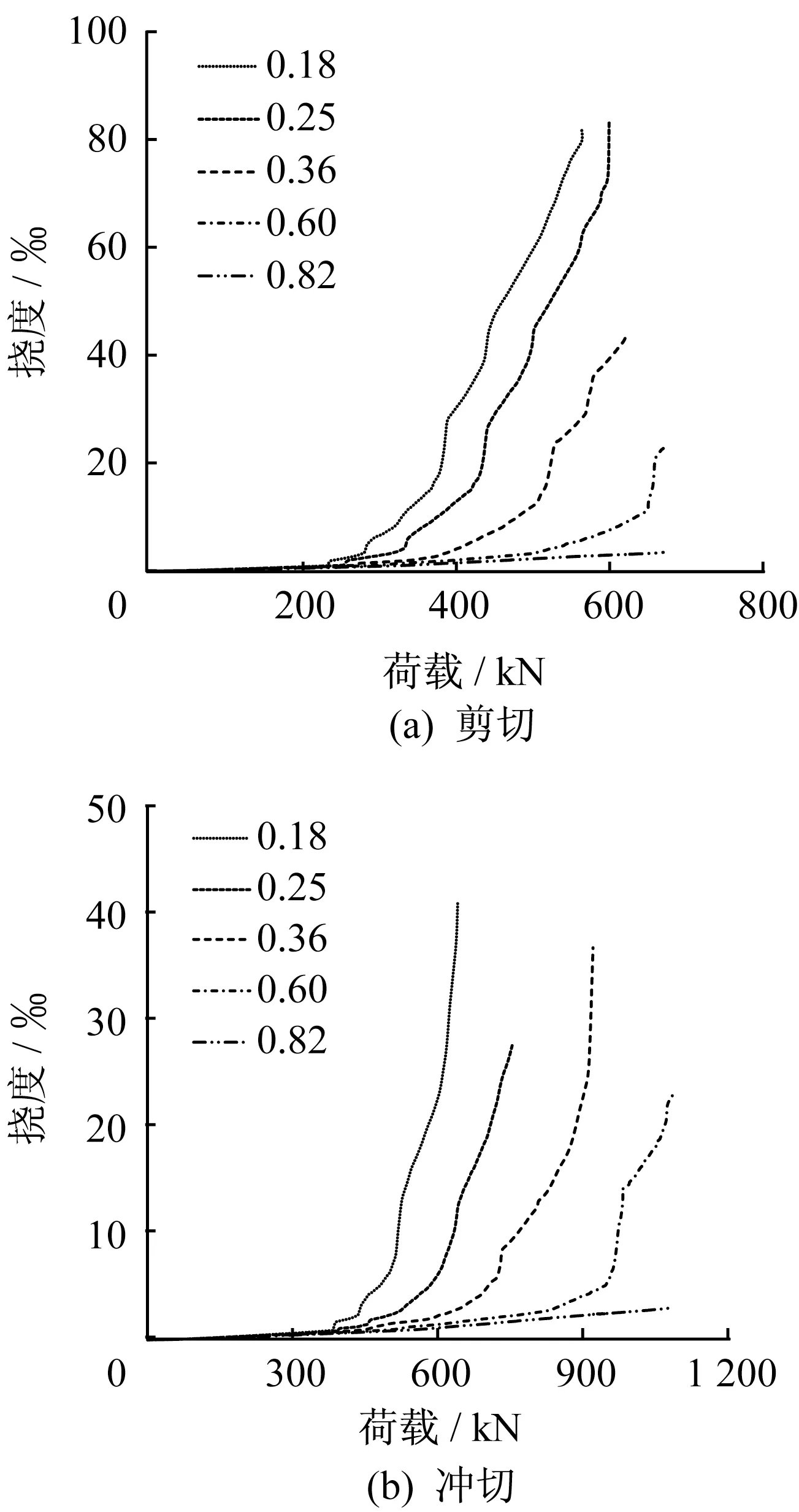
图12 不同配筋率下基础的荷载-挠度曲线对比Fig.12 Load deflection curves of bases with different reinforcement ratio
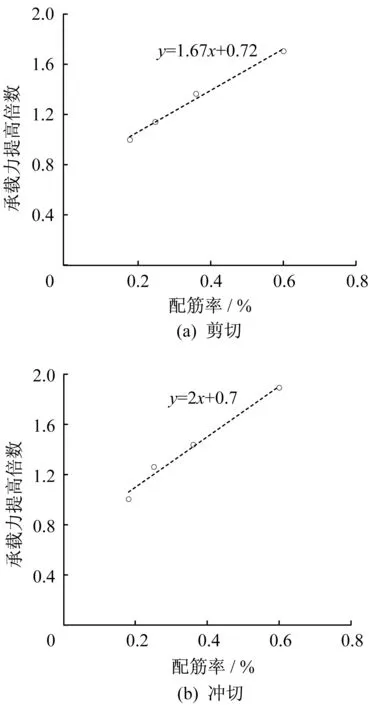
图13 承载力随配筋率的变化情况Fig.13 The variation of bearing capacity with reinforcement ratio
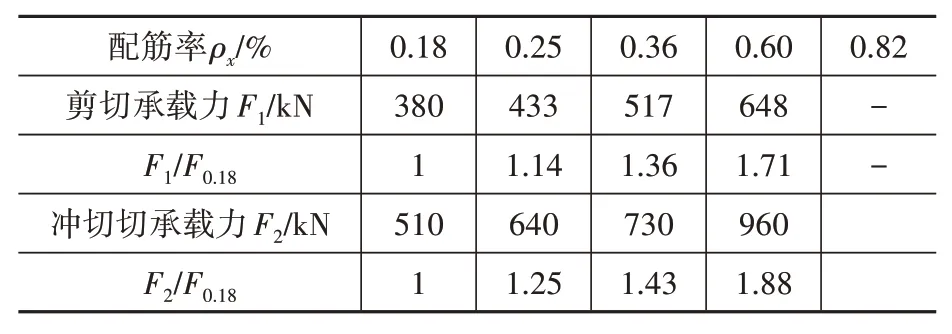
表6 不同配筋率下基础的承载力Table 6 Bearing capacity of bases with different reinforcement ratio
7 结 论
通过本文的分析,得到如下主要结论:
(1)对独立基础设计时,美、欧、日规范要求同时验算剪切和冲切承载力,按最不利进行设计,而我国规范通过B和b+2h0的大小关系,决定是按冲切或剪切承载力进行设计。
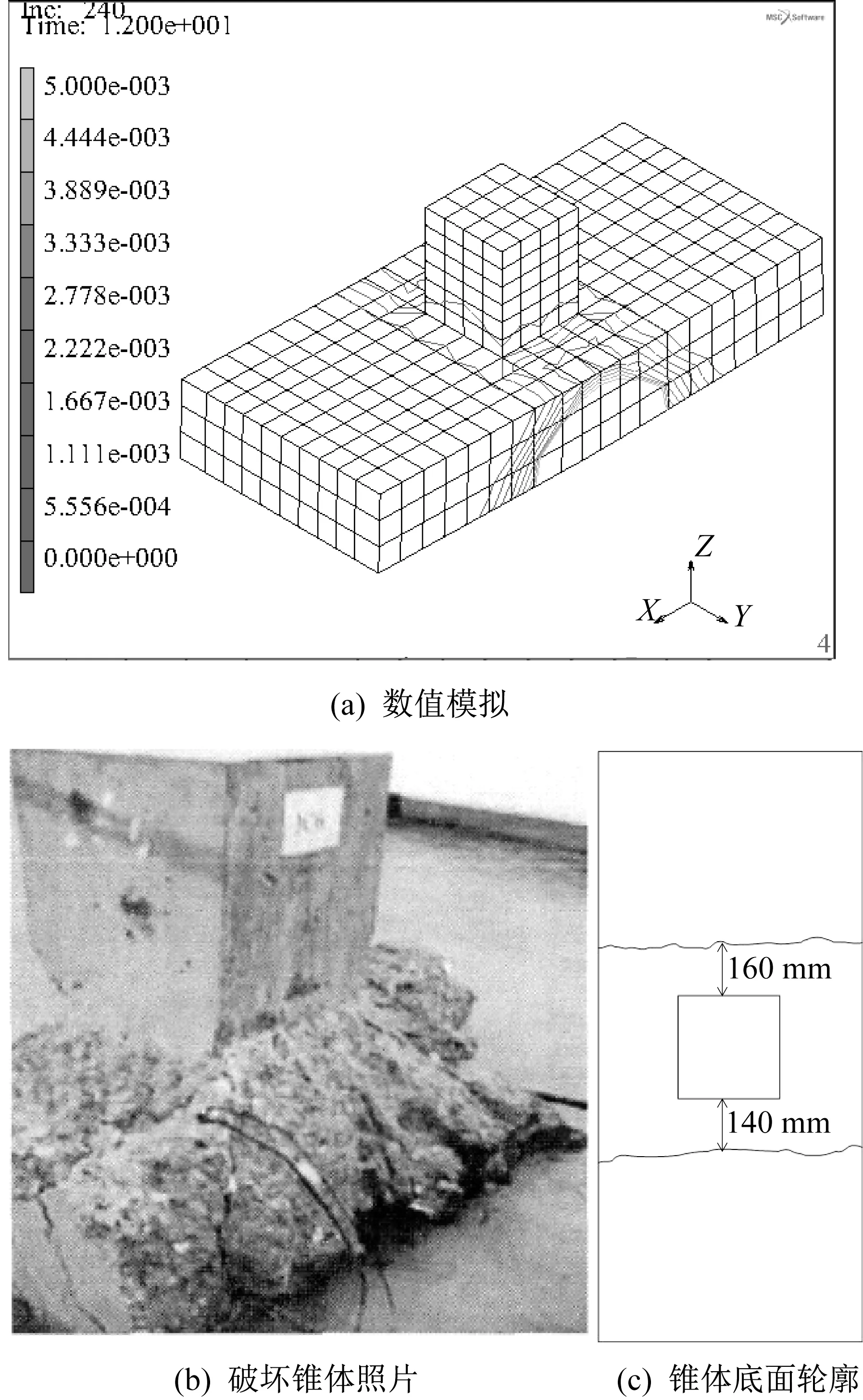
图9 数值模拟和试验得到的基础JC6剪切破坏对比Fig.9 Comparison of shear failure between numerical simulation and experiment of JC6
(2)对于冲切承载力验算,我国规范采用验算最不利侧斜截面的冲切承载力的“局部破坏模式”,美、欧、日规范验算临界控制截面的“整体破坏模式”。
(3)控制截面位置不同。对于剪切控制截面,我国规范取柱边处,美、欧规范取距柱边1倍基础有效高度d处,日本规范取距柱边0.5倍基础截面高度h处;对于冲切控制截面,中、美、日规范均取距柱边0.5d处,欧洲规范取距柱边2d处。
(4)冲切锥斜截面与底面夹角不同。中、美、日规范该夹角为45°,欧洲规范为26.6°。因此,某些根据我国规范需要验算的控制截面,根据EU2的规定可能不需要进行验算。
(5)冲切锥底面的形状不同。欧、日规范将其定义为距离有效加载面最近点等于规定距离的曲线,与真实破坏状态较为接近。中国和美国规范则有所简化,将其定义为由平行于有效加载面直线段围城的多边形,以便于设计和配置抗冲切钢筋。
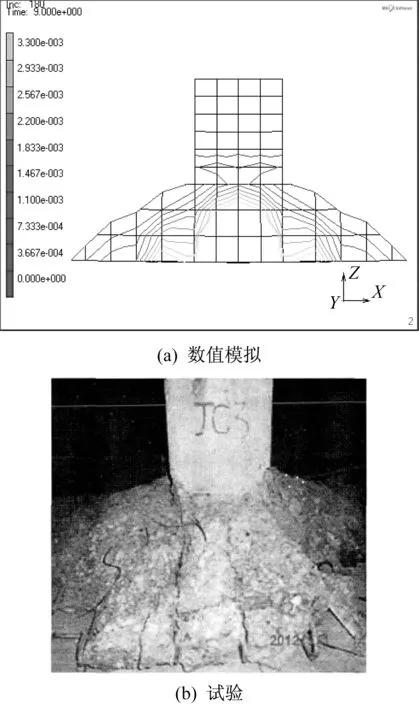
图10 数值模拟和试验得到的基础JC3冲切破坏对比Fig.10 Comparison of punching failure between numerical simulation and experiment of JC3
(6)各规范冲、剪承载力影响参数不同,例如美、欧、日规范考虑了配筋率的影响,而中国规范未考虑等。
(7)通过算例分析可知,我国规范的计算破坏模式与试验吻合最好;当基础配筋率小于1.65%时,ACI318-19小于ACI318-11的计算结果。另外,当配筋率较大时,各国设计结果更加保守,说明美、欧、日规范虽考虑了配筋率的影响,但考虑得不够充分,使得设计结果留有更大的余地。此外,对于同一基础,按不同规范计算得到的破坏模式不尽相同。
(8)通过MSC.Marc有限元软件对配筋率对基础冲切、剪切承载力的影响进行了参数分析,结果表明,当纵筋配筋率不大于0.6%时,配筋率每增加0.2%,剪切承载力提高0.334倍,冲切承载力提高0.4倍。

