带翼缘十字形截面轴心受压构件扭转失稳边缘屈服荷载研究

张仲祥 宋振森 陈行威

（上海交通大学船舶与建筑工程学院，上海 200110）

0 引言

带翼缘十字形截面构件具有各向等稳定、抗扭刚度高、对称美观以及施工便利等优势，深受建筑师的青睐。S.P.Ngian等［1］对一个8层的无支撑半刚性刚框架按照WMM（wind-moment method）法进行了设计，对比分析表明，柱截面采用带翼缘十字形截面构件比采用H型钢柱能够节约24%～66%的钢材。从截面的几何形状上看，带翼缘十字形可以看作是附加了翼缘的十字形截面，在轴心压力作用下的破坏模式以扭转失稳为主。目前对于此类构件的相关研究相对较少，仍处于初步探索阶段。H.R.Naderian等［2］利用有限条法对FRP材料组成的带翼缘十字形截面轴心受压构件进行了数值分析，发现该类构件在轴心受压时极易出现扭转失稳。

初始扭转是影响该类构件扭转失稳承载力的主要几何缺陷。随着轴力的增大，扭转角会增大，当构件轴压力增大到一定程度时，构件截面的边缘首先进入屈服，构件的刚度会迅速降低，虽然尚未达到构件的极限承载力，但已不适合继续加载，因此可将边缘屈服作为钢构件失稳的标志。本文从带翼缘十字形截面轴心受压构件的弹性扭转出发，推导其扭转失稳的边缘屈服荷载，并据此给出稳定曲线。

1 边缘屈服荷载

1.1 截面形式及相关参数

带翼缘十字形构件的截面参数如图1所示。为便于分析，截面高度取上、下两块翼缘中线的间距，截面宽度和各板件厚度均取实际数值，分析时均忽略焊缝、倒角和微小重叠部分。

图1 带翼缘十字形截面尺寸示意Fig.1 Dimension of Stiffened Cruciform Section

1.2 等效应力

构件轴向的正应力σz由三部分组成，分别是轴心压力P所产生的正应力σp、残余应力σγ和翘曲应力σω，因此轴向的正应力σz可以写作［3］

剪应力τ则由翘曲扭转剪应力和自由扭转剪应力组成，可以写作

式中，φ(z)为构件轴心受压的扭转位移函数。

对带翼缘十字截面构件截面，在翼缘处ω最大，故此处的翘曲应力σω最大，扭转时首先屈服。由带翼缘十字形截面的中心对称性，可仅考虑在-h/2处的翼缘。根据符拉索夫薄壁构件理论，将ω和Sω的表达式带入式（1）、式（2）可得到正应力和剪应力为

采用Von-Mises屈服准则，其等效应力可以写作［4］

因此可得-h/2处翼缘上的等效应力为

1.3 边缘屈服荷载

实际上构件屈服前扭转位移及其各阶导数以及残余应力均为小量，式（6）中含有φ′、φ′′、φ′′′高阶项均可略去，并可将式中残余应力单独移出进行简化处理，于是式（6）可写成

带翼缘十字形截面轴心受压构件仅考虑初始扭转缺陷的扭转位移函数可取为［5］

Aφ为初始扭转缺陷的幅值，即构件跨中处的初始扭转角。

根据式（8）可得

将式（10）代入式（7）即可得到带翼缘十字形构件的应力分布。以截面H248×124×5×8组成的长度为3 m的构件承担1 500 kN轴心压力时翼缘板的等效应力如图2所示。

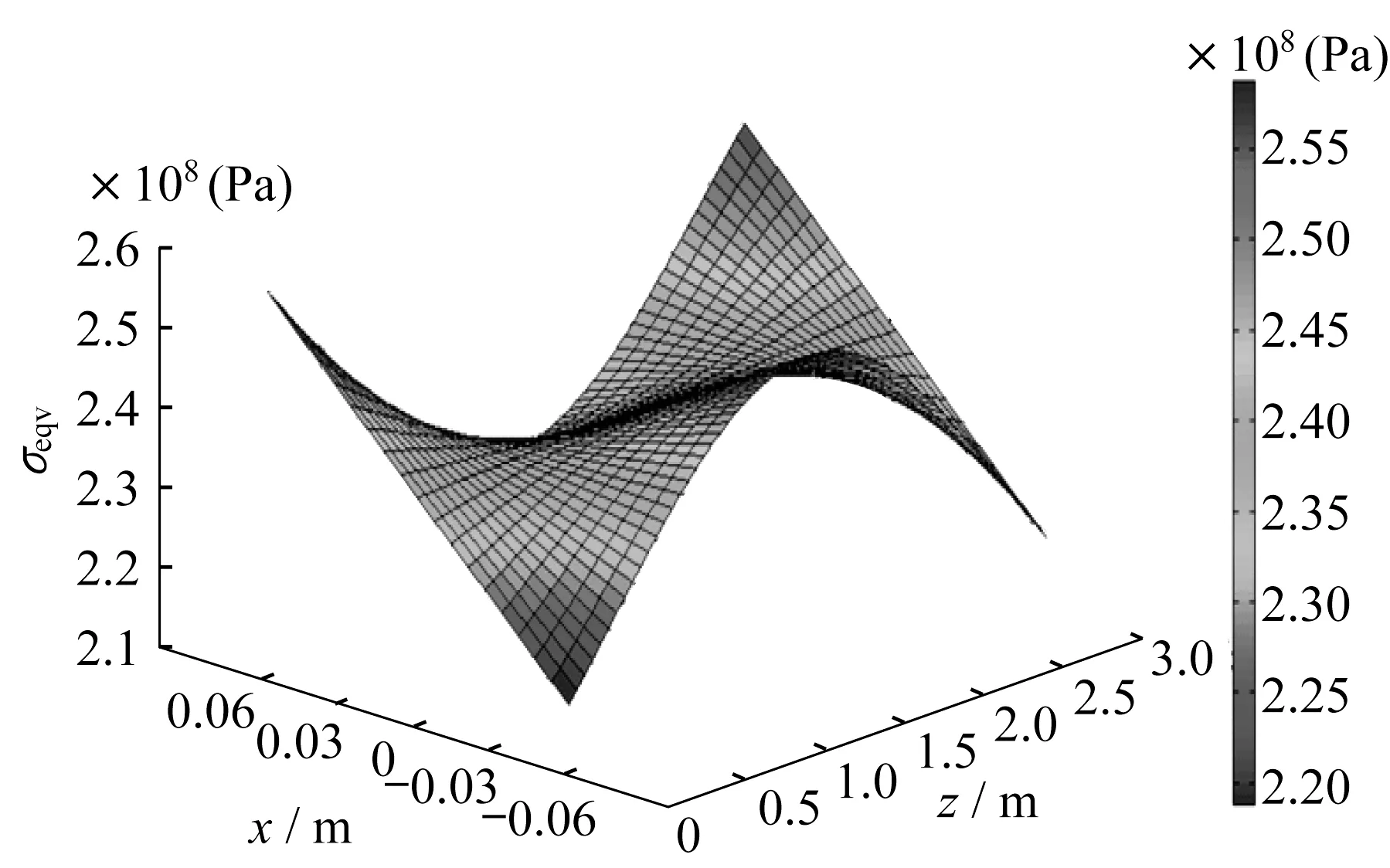
图2 翼缘板的Mises应力图（轴侧）Fig.2 Mises stress diagram of flange（axonometric view）

由图可以看出，翼缘Mises应力的最大值发生在两端和跨中的翼缘最外一侧，因此将(z，x)=(0，b2)带入式（10），然后再带入式（7）可得

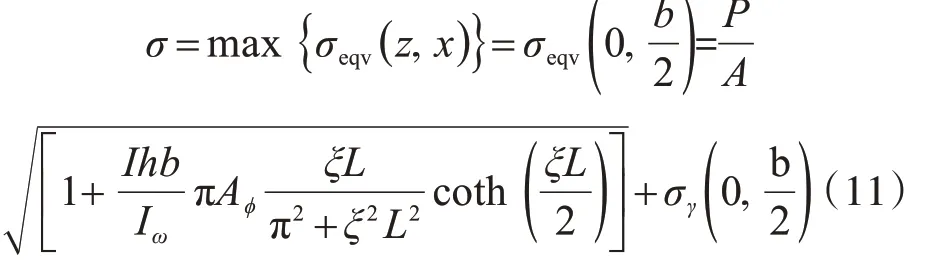
假定翼缘残余应力为线性分布，取翼缘边缘处的残余应力σγ的值为0.3fy，根据边缘屈服准则的定义，令式（11）等于屈服应力fy，可得边缘屈服荷载为

图3 翼缘板的Mises应力图（俯视）Fig.3 Mises stress diagram of flange（top view）

图4 翼缘板的Mises应力图（正视）Fig.4 Mises stress diagram of flange（front view）

由图5所示，当其扭转失稳临界力与扭转计算长度有关，随着长度的增加，其失稳模式会发生改变。两端曲线的交点处弯曲失稳临界力和扭转失稳临界力相等，此时构件的长度记为L1，当构件的长度L＜L1时，构件的破坏模式为扭转失稳，当L＞L1时，构件的破坏模式为弯曲失稳。

图5 带翼缘十字形截面轴心受压构件的失稳模式变化示意Fig.5 The relationship between the buckling mode and length

1.4 公式验证

为验证本文方法的可行性用式（12）计算一组带翼缘十字形轴心受压试件的边缘屈服荷载并与试验结果对比［6］，采用长度为3 m的热轧窄翼缘H型钢HN248×124×5×8切割焊接组合而成，试件在轴心压力的作用下发生扭转屈曲破坏。根据材性试验结果，钢材的弹性模量E=2.20×105MPa，屈服强度fy=350 MPa。

试验结果与式（12）的对比见表1，由表中结果可知，公式结果与试验结果吻合较好，可用本文边缘屈曲荷载代表扭转屈曲稳定承载力。

表1 扭转失稳承载力结果对比Table 1 Comparison of torsional instability ultimate load

1.5 扭转稳定系数

由式（12），仅考虑初始扭转缺陷的带翼缘十字形轴心受压构件的扭转屈曲稳定系数定义如下：

为考察翼缘宽度、腹板高度、翼缘厚度、腹板厚度等不同截面参数以及扭转长细比、弯曲长细比和弯扭长细比等不同变量对扭转屈曲稳定系数的影响，针对不同截面参数和长度构件计算其边缘屈服荷载，选取的截面参数如表2所示，计算时取初始扭转角，扭转长细比λω、弯曲长细比λx和弯扭长细比λxω定义如下：

表2 构件截面参数Table 2 Summary of section properties

根据计算结果绘制扭转长细比λω、弯曲长细比λx和弯扭长细比λxω下的扭转边缘屈服稳定系数的关系曲线如图6-图8所示。由图可以看出，以弯曲长细比λx和弯扭长细比λxω为自变量时，扭转边缘屈服稳定系数曲线有较大离散性，而当采用扭转长细比λω作为自变量时，不同截面的扭转边缘屈服稳定系数曲线规律性明显。可见扭转边缘屈服稳定系数与扭转长细比有较强的相关关系，可认为是扭转长细比λω的函数。同时显示带翼缘十字形截面轴心受压构件的翼缘宽度、腹板高度、翼缘厚度以及腹板厚度等截面参数对边缘屈服稳定系数没有独立的影响规律。

图6 扭转长细比与扭转边缘屈服稳定系数的相关曲线Fig.6 The curve of non-dimensional first-yield load vs.torsional slenderness

图7 弯曲长细比与扭转边缘屈服稳定系数的相关曲线Fig.7 The curve of non-dimensional first-yield load vs.flexual slenderness

图8 弯扭长细比与扭转边缘屈服稳定系数的相关曲线Fig.8 The curve of non-dimensional first-yield load vs.flexural-torsional slenderness

2 扭转边缘屈服荷载的简化公式

2.1 简化公式推导

式（12）隐式方程求解过程复杂，不便于实际的应用，因此本文推导出显示表达的扭转边缘屈服荷载简化表达式。

展开可得关于Pcr，1的三次方程

因为m＜0，由Cardano公式可以得到三个根的三角函数形式为

通过证明Pcr，13为三个根中最小的正实数根，因此可得到边缘屈服荷载显示表达式的近似解为

2.2 简化公式正确性验证

为验证本文简化公式的正确性，选用H248×124×5×8截面作为算例，用式（24）和式（12）分别计算不同长度下带翼缘十字形轴心受压试件的边缘屈服荷载，对比如图9所示。

图9 扭转边缘屈服稳定系数的隐式精确解与拟合公式公式的比较Fig.9 The comparison of exact solution and approximate solution

由图9可见，在可能发生扭转失稳的区间，简化公式与精确的最大误差Δ=0.03，且近似解都小于精确解，在工程应用中采用简化公式是可行的。

3 结论

（1）采用金属材料的Von-Mises屈服准则，并略去翼缘板Mises应力表达式的高阶小量后推导出了带翼缘十字形截面轴心受压构件的边缘屈服荷载的隐式表达式，并通过试验对比，验证了隐式表达式的正确性。

（2）通过对比翼缘宽度、腹板高度、翼缘厚度、腹板厚度等不同截面参数以及扭转长细比、弯曲长细比和弯扭长细比等不同变量发现，不同构件的扭转失稳边缘屈服荷载在使用弯曲长细比或弯扭长细比来描述时有较大的离散型，而当以扭转长细比为自变量时，不同截面的曲线则表现出明显的规律，可见带翼缘十字形截面轴心受压构件的扭转失稳问题应通过扭转长细比来研究。同时显示带翼缘十字形截面轴心受压构件的翼缘宽度、腹板高度、翼缘厚度以及腹板厚度等截面参数对边缘屈服稳定系数没有独立的影响规律。

（3）将隐式表达的边缘屈服荷载表达式通过Taylor展开进行了简化，得到了边缘屈服荷载显式表达式（24）。