基于MEMS传感器的磁梯度张量单点定位系统

修春晓，周 瑜，李 光，钟华森，李成豪

(中国电子科技集团公司第三研究所，北京 100015)

0 引言

磁目标单点定位是通过观测和分析由探测对象磁性差异所引起的磁异常，进而获取磁性目标如距离、速度和位置等参数的一种探测方法。随着磁测技术与数据处理技术的发展，磁测的发展可分为以下三个阶段[1]：磁总场强度测量、磁总场强度梯度测量以及磁场矢量与磁梯度张量测量，这三个阶段由低到高可以获得更多的磁异常信息。其中，磁梯度张量测量具有对地磁场不敏感，能够区分出磁异常体的大小与和形状，可延伸出多种数据处理算法，准确地勾勒出异常源边界等优点[2]，可以通过磁梯度张量单点定位技术，实现对磁异常体定位，该技术具有隐蔽性好、虚警率低、探测针对性强的特点，可广泛应用于无人值守区域的国土监视、反潜战、全天候智能交通系统等领域[3]。

随着磁测理论和传感器技术的发展，基于磁梯度张量测量的定位与跟踪技术逐渐代替基于磁矢量测量[4-5]的跟踪方法。自1972年W. M. Wynn[6]首次提出利用磁梯度张量矩阵反演定位磁偶极子的方法以来，C. P. Frahm[7]，W. M. Wynn[8]，P. W. Schmidt[9]以及尹刚[10]等相继提出了利用磁梯度张量矩阵与磁场矢量单点定位磁偶极子的方法。为消除地磁场及其他共模干扰对单点定位精度的影响，2012年李光等[11]在欧拉反褶积公式[12]的基础上提出了基于差分的磁偶极子单点张量定位方法，但对磁梯度张量差分后，幅值在数量级上大大降低，这提高了对系统测量精度的要求；2007年Wiegert等[13]提出了基于不变量的STAR单点定位方法，通过利用多个探测点磁梯度张量不变量之间的比值关系进行定位，在随阳轶[14]、吕俊伟[15]等改进下，消除了原定位方法中不变量存在的椭圆误差对定位精度的影响，可有效提高定位精度，但新构造的不变量梯度，由于随距离六次方衰减，系统有效探测距离也大幅降低。基于五棱台或六棱台结构的测量模型多应用于高低温超导全张量磁梯度测量系统中，郑婷[16]、伍俊[17]和申茂东[18]等人对磁梯度测量模型进行了深入研究，超导全张量磁梯度测量系统具有测量灵敏度高、噪声水平低和探测距离远等显著优点。但是，上述基于常规磁通门传感或高低温超导技术搭建的磁梯度张量测量系统均存在整机尺寸大、系统运行维护成本高等问题，很难实现小型化和低成本化应用。本文针对此问题，提出了基于MEMS传感器的磁梯度张量单点定位系统。

1 MEMS磁通门磁场传感器与磁梯度张量

1.1 MEMS磁通门磁场传感器

磁传感器是非常重要的磁场探测传感元件，传感器应用范围广泛。霍尔效应传感器和磁通门传感器是磁场传感中最常见的两类传感器，磁通门传感器相较于霍尔效应传感器具有更高的灵敏度、更低的漂移、更低的噪声和高线性度，它能够检测到磁场中非常细微的变化。

磁通门传感器利用被测磁场中高导磁铁芯在交变磁场的饱和激励下，所产生的磁感应强度与磁场强度的非线性关系来测量弱磁场。MEMS磁通门传感器技术的关键就在于将三维螺旋式线圈这一复杂机械机构芯片化的同时还需要使用较厚的金属线以降低整个线圈电阻值。此外如图1所示，磁通门传感器还需带有必要的传感器调节和补偿线圈内部关闭控制回路，在其反复驱动进入和退出饱和时，能够支持无滞后运行，确保传感器达到稳定的增益和高线性度。

图1 MEMS磁通门传感器线圈及补偿电路示意图Fig.1 MEMS fluxgate sensor coil and compensation circuit schematic diagram

图2为基于MEMS单轴磁通门传感器芯片图，芯片封装尺寸4 mm×4 mm，磁场可由其内部磁通门传感器直接检测，该设备集成了传感器输出，可确保高回路增益。

图2 MEMS磁通门传感器芯片图Fig.2 MEMS fluxgate sensor chip

1.2 磁梯度张量及其特性

磁梯度张量的各个元素分别是磁场矢量三分量在三个相互正交方向上的空间变化率，即磁总场B的矢量Bx、By、Bz在空间x、y、z三个方向上的变化率构成了二阶张量矩阵G，可表示为：

(1)

磁总场、磁矢量以及磁梯度张量在直角坐标系中的关系如图3所示。

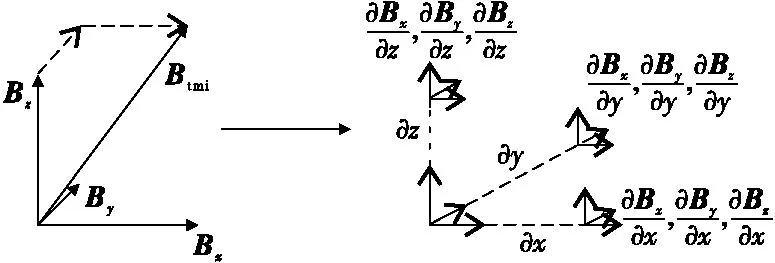
图3 磁总场、磁矢量(左)与磁梯度张量(右)间关系Fig.3 Total magnetic field, magnetic vector (left) and magnetic gradient tensor (right)

在无源空间中，磁总场B的散度及旋度为0，即满足无迹性和轴对称特性，式(2)、式(3)成立。

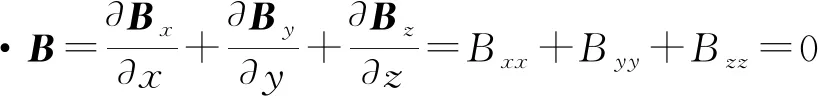
(2)

(3)

磁梯度张量矩阵的9个元素中只有5个是独立的，磁梯度张量矩阵的特征值与坐标系的选择无关，为张量的基本不变量，且张量的其余不变量也可由特征值表示。设矩阵G的3个特征值为λ1，λ2和λ3，对应的特征向量为V1、V2、V3，则由G的特征方程可得磁梯度张量的另外4个不变量，分别表示为：

(4)

(5)

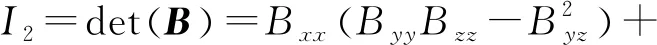
(6)

(7)

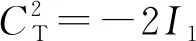
(8)

式(8)中，

(9)

磁梯度张量矩阵的3个特征值满足|λ1|≥|λ3|,|λ2|≥|λ3|且λ2≥λ3≥λ1成立。磁偶极子梯度张量场的向量示意图如图4所示，磁偶极子位置矢量与磁矩矢量的夹角余弦值为：

(10)

将式(10)代入磁异常总场的模值与约缩量当中，可求取得到位置矢量模值r与磁矩矢量的模值M。

(11)

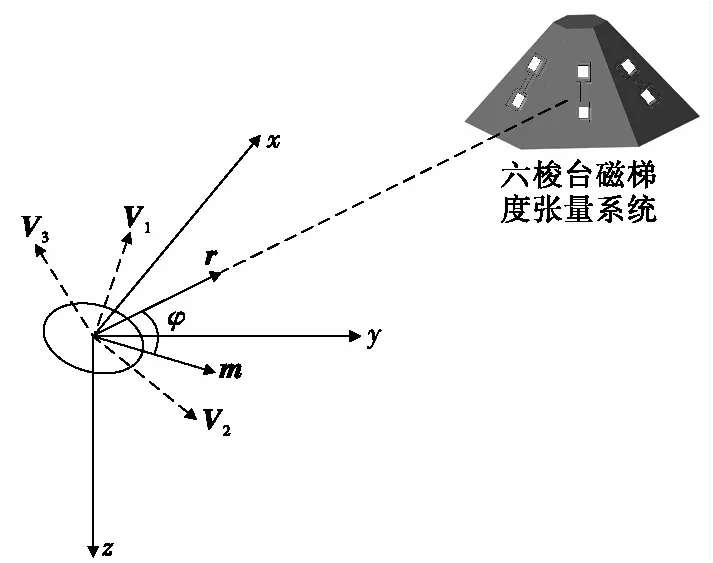
图4 磁偶极子梯度张量场的向量示意图Fig.4 The gradient tensor of magnetic dipole

2 基于MEMS传感器的磁梯度张量单点定位系统

2.1 基于平面梯度计的六棱台磁梯度张量测量模型

由于MEMS磁传感器为单轴传感器，采用两个MEMS磁传感器可构建单轴方向梯度计。图5为六棱台磁梯度张量探头结构图，6个棱面上各布置一个平面梯度计。

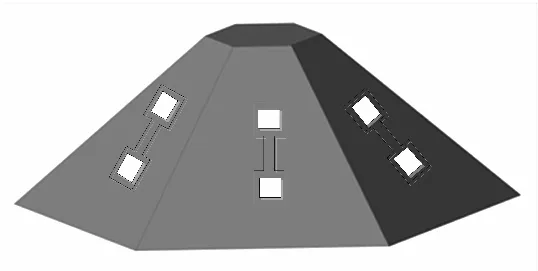
图5 六棱台磁梯度张量探头结构图Fig.5 The magnetic gradient tensor probe based on hexagonal prism model

图6为磁梯度张量测量探头坐标图，平面梯度计轴向为x轴，那么该轴上梯度值可表示为：

(12)

式(12)中，U为张量探头处的标量磁位。

图6 磁梯度张量测量探头坐标图Fig.6 The probe coordinates for magnetic gradient tensor measurement

由梯度计在张量探头上的布置方式可知，探头坐标系与各梯度计坐标系的对应关系可表示为：

(13)

将式(13)带入式(12)中，可得Gk与B各分量的函数关系式，表示为：

(14)

由式(14)可知，Gk为关于B的线性方程。任意5个梯度计的线性方程可联立成方程组，可表示为：

(15)

式(15)中，矩阵F的第k行行分量可表示为：

F(k,5)=sinφkcosθksinθk。

采用最小二乘法求解上述方程组即可从5个梯度计测量值中提取出B的各分量值。

2.2 磁梯度张量测量单点定位算法

由对称矩阵的特征向量之间的几何关系可知，向量V1，V2，m和r共面，且4个向量之间可互相表示，令

r=α1V1+α2V2

(16)

m=β1V1+β2V2

(17)

又磁偶极子产生的梯度张量场与矢量场满足欧拉反褶积公式，且构造指数为3，推导可得到α1和α2：

(18)

磁偶极子位置矢量的单位向量可表示为：

(19)

可进一步求得β1和β2：

(20)

上述反演方法不仅得到了磁偶极子真实位置及磁矩矢量，而且还得到了另外三组虚假解，首先可根据所测目标在磁梯度张量系统的上方或下方，直接去除其中两个虚假解，然后根据磁梯度的张量系统测得的多点总磁场强度及磁矢量场进行另一个虚假解的去除。

2.3 基于MEMS传感器的磁梯度张量单点定位系统构建

在完成MEMS磁梯度张量系统设计后，采用DRV425传感器和六棱台进行了探头搭建，磁传感器参数如表1所示，磁梯度计和磁梯度张量探头分别如图7和图8所示。在室内环境对该系统进行了初步的静态实验测试。

表1 磁传感器参数

图7 磁梯度计电路板图与实物图Fig.7 The circuit board and physical photos of magnetic gradiometer

图8 MEMS磁梯度张量探头实物图Fig.8 The physical picture of MEMS magnetic gradient tensor probe

3 系统静态实验

为测试系统性能并验证其有效性，如图9所示：将六棱台测量探头固定，首先将磁性铁球从距离探头15 cm位置处沿探头中心轴线方向向外滑动远离探头，最后达到60 cm左右处，如轨迹1所示；然后将磁性铁球沿垂直探头中心轴线方向，从左向右滑动，如轨迹2所示；最后通过采集的磁场数据对磁球坐标位置进行估算。磁球真实位置与估算位置分别如图10和图11所示，由于系统所采用的单点性定位方法基于磁性目标磁偶极子假设，因此在使用时系统与磁性目标距离需保持一定距离，以满足假设条件，经测试系统定位误差总体控制在10%以内。

图9 静态实验测试环境图Fig.9 The static test environment diagram

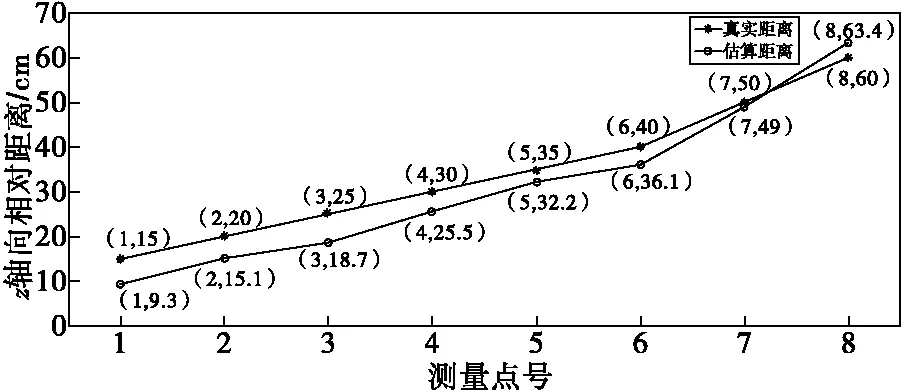
图10 z轴方向铁球与磁梯度张量探头实际距离与估算距离图Fig.10 Actual distance and estimated distance between iron ball and magnetic gradient tensor probe in z-axis direction

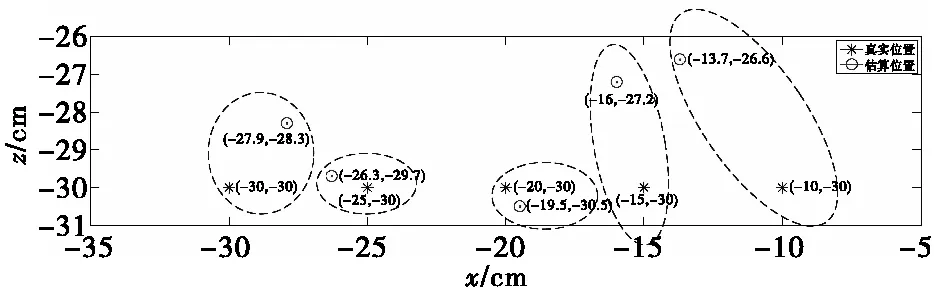
图11 x轴方向铁球真实位置与估算位置点位分布图Fig.11 Actual distance and estimated distance between iron ball and magnetic gradient tensor probe in x-axis direction

4 结论

本文提出基于MEMS传感器的磁梯度张量单点定位系统，该系统采用六棱台式磁梯度张量探头结构设计，利用两个单轴MEMS磁传感器以差分形式构建梯度计，根据六棱台磁梯度张量测量模型解算当前位置磁梯度张量值，通过磁梯度张量单点定位算法计算出磁性目标磁矩与相对距离，进而求解磁矩矢量和位置矢量，最终完成磁性目标定位。静态实验结果表明，基于MEMS传感器的磁梯度张量单点定位系统可有效实现近距离范围内磁性目标探测与定位，系统具有实时性强、成本低和尺寸小等优点，同时它也可作为小型样机，验证六棱台式超导全张量磁梯度测量系统磁性目标单点定位有效性。