基于维特比算法的引信多普勒信号频率估计方法

王正顺，宋 萍，唐 强，余孝安

(1.北京理工大学机电学院，北京 100081；2. 西安机电信息技术研究所，陕西 西安 710065)

0 引言

脱靶量是指导弹等在与靶标相遇过程中，弹体和靶标交会瞬间相距的最小距离，是在武器系统研制过程中反映制导精度的一个重要参数。目前在靶场试验中主要使用的脱靶量测量方法有光学测量、声学测量、GPS(全球定位系统)测量等方法[1-2]。这些测量方法测量精度虽然较高，但都需要配备专用设备，且数据处理比较复杂，不能在靶场试验后快速提供测量结果。而利用导弹或炮弹自身携带的多普勒体制无线电引信在交会过程中获取的连续波无线电多普勒信号进行事后处理，则可以快速地得到估算的标量脱靶量[3]。在多普勒无线电脱靶量测量方法中，事后多普勒信号的频率估计是关键的研究方向之一。文献[4]对基于多普勒频率的脱靶量参数估计方法的可观测性及估计性能进行了分析，证明了利用时序多普勒频率进行脱靶量估计的全局可观测性，为利用此方法的脱靶量测量技术提供了参考。文献[5]提出了基于短时傅里叶变换(short time fourier transform，STFT)和经验模态分解(empirical mode decomposition，EMD)的多普勒信号处理算法，但是EMD分解时会有模态混叠和端点效应[6]，会影响其频率提取的精度。

因此，本文提出基于维特比算法的引信多普勒信号频率估计方法，能够较为准确地实现对连续波无线电多普勒信号频率的快速事后估计，同时实现脱靶量的测量。

1 相关研究基础

1.1 交会条件下连续波无线电引信回波信号特性

根据文献[4,7]的相关理论和实验分析可知，交会条件下，由于弹目间存在相对运动，连续波体制无线电引信的回波信号为连续波无线电多普勒信号，属于典型的非平稳信号。其多普勒分量的频率变化规律为：在远场区，信号的频率基本不变；而在近场弹目交会的过程中，弹目距离越小，信号的频率越小且频率降低得越来越快，幅值逐渐升高且升高得越来越快。

实际上，随着弹体与靶标的距离逐渐减小，受近场运动物体的电磁散射特性影响[8-9]，近场区的被测目标不再能被视为点目标，所以引信实际接收到的多普勒信号是往往有一定带宽的，且由多个难以分别提取的分量组成，这对多普勒信号的处理增加了难度。但考虑到目标上各反射无线电波的散射点是相对固定的，所以在计算误差允许的范围内，可将最强散射点的位置作为目标的位置，以降低体目标效应对交会参数估算的干扰。并且在飞行试验中，弹上引信接收的回波信号往往会包含一定的噪声成分和跳变的野值，这些都会增大多普勒频率估计的误差[9-10]。

为保证研究的针对性，本文仅讨论如何利用信号本身的特性，在存在一定噪声干扰的信号中，估算连续波无线电引信多普勒信号的频率和脱靶量参数的问题，简化有关无线电波反射特性给多普勒信号处理带来的相关影响。

1.2 信号时频分析方法的选择

在目前常用的非平稳信号时频分析方法中，小波变换在信号的高、低频处的时频表现有所差别，在频率较高时，信号的聚集性不好；STFT则不论是对单分量信号还是多分量信号，都有较好的时频聚集性，且信号在时频重叠点处不易相互干扰[11]；S变换虽然在时频重叠点处也有较好的表现，但是在高频处会出现扩散问题；维格纳-威尔时频分布(wigner-ville distribution，WVD)的时频聚集性最好，但在处理多分量信号时又会存在明显的交叉项干扰的问题[12]，在其基础之上改进的伪维格纳-威尔时频分布(pseudo wigner-ville eistribution, PWVD)虽然进行了一定的平滑处理，但仍无法完全避免该问题，这不利于后续信号特征的提取。

因此本文首先采用STFT对连续波无线电多普勒信号进行处理，得到信号的时频分布，然后通过能量收缩和阈值处理，提高信号的时频聚集性，降低噪声信号成分的干扰；再对得到的时频谱图中的时频分布点按照能量分布情况进行检测定位，识别出所得到的二维时频谱图中能够反映多普勒信号时间频率变化关系的特征点，进而可得到信号的频率估计。

1.3 Viterbi算法的基本思想

文献[13]提出了借鉴解决隐马尔可夫模型问题的Viterbi算法，该算法的思想是通过设置惩罚函数对瞬时频率轨迹进行识别和跟踪。该方法在用于瞬时频率估计前，应先满足以下两个假设：

1) 瞬时频率点所对应的时频分布点的能量值尽可能的大；

2) 两个连续的瞬时频率点的频率的差值不是特别大，即信号的瞬时频率曲线是比较平滑的[13]。

显然，连续波无线电多普勒信号满足上述使用条件。依据Viterbi算法的思想，瞬时频率的估计值可以用使路径代价函数值之和最小的路线表示，即瞬时频率的估计曲线是使所设置的代价函数的值之和最小的点的集合。这种方法能够在高噪声环境下依然表现出良好的性能，但稳健性不足，容易受到信号中包含的噪声信号的影响。本文在上述原Viterbi算法的基础上，对其进行了改进，提高了算法的针对性，在提取多普勒信号频率和进而计算脱靶量数值时具有较高的准确度。

2 算法描述与实现

本文提出一种在STFT基础上，结合阈值处理和Viterbi方法的新型多普勒频率的测量方法，利用所接收的连续波无线电多普勒信号，进行时频分析并提取出其时频特征，再利用信号的模型函数进行回归分析，可以方便地得到多普勒频率估计和脱靶量等交会参数。

2.1 算法流程描述

本文提出的基于Viterbi算法的引信多普勒信号频率估计方法的主要流程如图1所示。

图1 基于Viterbi算法的引信多普勒信号频率估计方法流程图Fig.1 Flow chart of the frequency estimation method of fuze Doppler signal based on Viterbi algorithm

首先，将获取到的连续波无线电多普勒信号在合适的窗函数和窗口宽度下进行STFT变换，窗口宽度可根据所需要的时间和频率精度进行选取，得到该信号的时间-频率分布TF(i，f)；然后，将每个功率谱密度(power spectral density, PSD)估计值按照窗口函数的宽度进行重新分配，使其收缩到其能量重心的位置，得到每个PSD估计的重心频率和时间；再根据原信号的平均能量值和信号中预计的噪声信号的强度，选择合适的阈值信噪比作为参考，对上述步骤得到的时频分布点按照能量的阈值强度进行过滤，将强度值小于该信号阈值强度的点设置为零，这样可以过滤掉一些低能量的噪声信号点。

滤波的效果取决于选取的阈值是否合适，若选取的阈值过低，可能达不到去除噪声的效果；若阈值设置过高，则会除去多普勒信号中的有效信息，可能得不到足够的拟合点用于拟合曲线，影响后续的计算精度。因此在实际应用中，阈值大小的选取应根据信号预计的信噪比来估计和尝试，保证在去除一部分噪声的同时，能够保留足够多的有效信息供后续算法提取信息。

受不确定性原理和交叉项干扰的影响，单一的时频收缩分布处理后，信号的能量可能没有完全集中在实际的瞬时频率点上，并且仍可能存在一定的噪声成分，这些都会影响频率估计的精度，因此需要在此基础上利用改进的Viterbi方法进一步处理，尽量剔除偏离了真实曲线的时频点，以进一步提高频率估计的准确性。

Viterbi方法处理的过程是在得到的时频谱图中，按照设置的惩罚函数选出使得函数值最小的分布点，作为反映该多普勒信号的时频变化关系曲线的拟合点集；然后在该点集中，按照预先确定的函数模型进行非线性拟合，就可以计算出该多普勒信号的时间-频率关系的表达式，即得到了估算的多普勒信号频率。在非线性拟合时所使用的多普勒信号的函数模型中，多普勒信号的频率除了与引信本身特性，发射波的波长等因素相关外，还与交会速度和脱靶量等参数有关。因此，利用获得的多普勒信号的时间频率关系表达式，还可以估算出脱靶量等交会参数。

2.2 改进的Viterbi方法

本方法的关键在于改进的Viterbi时频特征点提取方法。在得到被测信号经过STFT和阈值处理后的时频图后，改进的Viterbi算法的多普勒频率提取方法所使用的路径代价函数可参考下述的代价函数：

(1)

式(1)中的各项代表不同的代价函数，式中的代价函数由三部分组成，分别是同时刻排位代价函数，相邻时刻平滑代价函数，和记录已选路径的路径累计和函数。

式(1)中g(k(n)、k(n+1))为相邻时刻平滑代价函数，其构建可以参考式(2)。

(2)

式(2)中，c为常系数，表示平滑代价函数的权重；Δ为允许波动值，其数值的选择取决于两相邻点间瞬时频率变化的最大允许值。在实际应用中，Δ的选择可基于预处理所使用的STFT变换的频率分辨率选取。

式(1)中h(TF(n,k(n)))为同时刻能量排位代价函数，其构建可以参考如下方法：首先，将所有时刻的TF值按能量大小排列，本文以非递增的顺序排列，即

TF(n,f1)≥TF(n,f2)≥…≥TF(n,fj)≥TF(n,fQ)

然后按照式(3)进行计算个点的排位代价函数值。

h(TF(n,fj))=m·(j-1)

(3)

式(3)中，j表示时频点在序列中的位置；N为该信号频率点的个数，且i=1,2,…,N；m为排位代价的权重参数。

3 仿真实验验证

3.1 实验与数据处理过程

由于无线电引信收到的多普勒频率真实值是无法精确测得的，因此也无法得知估算的多普勒频率和真实频率的偏差究竟有多少。但考虑到多普勒频率受脱靶量的影响，所以本文将利用估测的多普勒频率估算脱靶量，再与预先设置的脱靶量真值相比较，间接地验证本文方法对连续波无线电引信多普勒信号的频率估计的准确性。

在本实验中，首先设置好距离、交会速度、脱靶量、信号频率和波长等试验参数，得到仿真的模拟多普勒回波信号，然后在该信号中混合一定信噪比大小的高斯噪声，得到待测的仿真信号；再使用本文提出的方法进行脱靶量的求解，比照设定的脱靶量数值和实际的估算结果，即可验证本文提出的方法的准确性。

下面以脱靶量为2 m，交会速度为900 m/s，模拟信号中加入的噪声信号的信噪比为0 dB，即噪声的平均能量值和多普勒信号的平均能量值相等条件下的模拟实验为例，说明数据处理的过程。将原不含噪声的多普勒仿真信号与含噪的仿真信号均使用窗宽为512的三角窗进行STFT处理，得到信号的时频谱图，分别如图2和图3所示。

图2 仿真多普勒信号经STFT得到的时频图Fig.2 Spectrogram of simulated Doppler signal obtained by STFT

图3 带噪声的多普勒仿真信号经STFT得到的时频图Fig.3 Spectrogram of simulated Doppler signal with 0 dB noise obtained by STFT

图3为经STFT后的带噪仿真多普勒信号的时频图，可以看出，在信号的整个时频分布图中，各时刻的各个频率成分上都存在一定的噪声，虽然在信号的后半段，即目标接近靶标时，多普勒信号能量不断增大，尚可分辨出多普勒信号的频率变化，但由于模拟信号中的噪声成分的强度比较大，在模拟信号的起始段，其有效的多普勒成分几乎淹没在噪声信号中。因此，需要先使用本文的提取方法从时频分布中选取出合适的拟合点，才能进一步提高拟合运算的精度。

按照图1所述的算法流程，在信号经过STFT后，需要进一步进行处理：在每个窗口宽度内，将每个PSD估计值重新分配到其能量的重心，该处理能够在保证留有足够有效信息的情况下，适当提高信号的时频聚集性，处理结果见图4。

图4 收缩处理后得到的多普勒信号时频分布图Fig.4 Spectrogram of simulated Doppler signal obtained after shrinkage treatment

然后根据信号的平均能量值，选择合适的信噪比作为阈值用于去除噪声，此处选取的信噪比阈值为所加入的噪声的信噪比-32 dB。依据该阈值，对时频谱图进行滤波，去除STFT得到的时频图中的一部分噪声点，得到能量在该阈值之上的时频点集。再利用本文提出的基于Viterbi方法的特征点提取方法从上述的时频分布图中提取瞬时频率特征点。最后，按照多普勒信号表达式，进行非线性拟合。

改进Viterbi方法选取的特征点和拟合得到的多普勒信号拟合曲线和脱靶量参数的估计值均绘制在图5中。

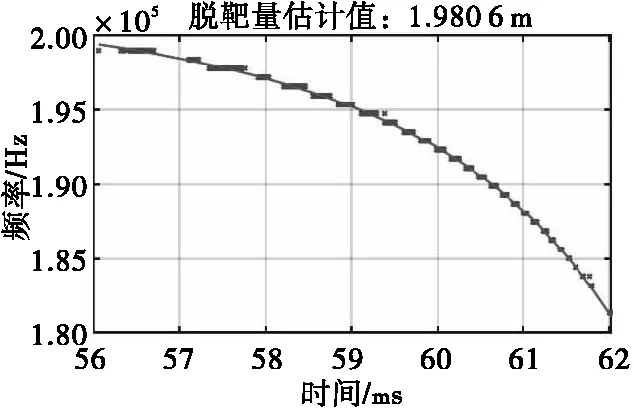
图5 选取的多普勒信号时频特征点与拟合曲线Fig.5 Time-frequency points selected from spectrogram and fitting curve of Doppler signal

图5中的黑色圆点为本文算法所提取的仿真多普勒信号的特征时频点，实线为拟合得到的多普勒信号的时频关系的部分曲线，同时也得到了该次实验的脱靶量估计值为1.980 6 m。该次实验预先设置的脱靶量为2 m，即本算法估算的脱靶量偏差为0.019 4 m，占实际脱靶量的0.97%。从估算结果可知，本文提出的方法能够较为准确地估算出脱靶量的值，也间接证明了本方法在多普勒信号中包含同等强度的噪声时，对连续波无线电引信多普勒信号的频率估计具有较好的准确性。

3.2 仿真实验结果分析

为进一步测试本文方法的有效性，以及测试不同强度的噪声对多普勒频率估计的影响，本文在脱靶量为2 m，交会速度900 m/s的条件下，进行了多次模拟仿真实验。通过向模拟信号中混入不同信噪比的噪声得到不同的模拟信号，再利用解算出的脱靶量估计值与真实值的偏差来评估多普勒信号频率的估计精度。

显然，当噪声信号的强度过大时，信号的多普勒成分会完全淹没在噪声成分中，因此本实验设置的带噪仿真信号的信噪比区间为-10～10 dB，按照0.1 dB的步长，进行了200次模拟试验。下面将所有有效的实验结果统计在图6中。图6的横纵坐标分别为模拟信号的信噪比和脱靶量估计值与真值的偏差，每个点代表一个脱靶量的估算偏差。

图6 不同信噪比噪声的仿真多普勒信号的脱靶量估算偏差Fig.6 Statistical chart of the deviation between the estimated miss distance and the real miss distance of simulated Doppler signals with different SNR noises

从图6可见，除去个别离散的试验点，整体的规律为：在模拟信号的信噪比较高(5 dB以上)时，脱靶量的估计偏差很小；随着信噪比不断减小，即仿真信号中的噪声成分逐渐增强时，脱靶量估计值的偏差也逐渐增大，这与常识相符合。但在噪声强度较大(信噪比低于0 dB)时，脱靶量的估计值偏差仍在10%的误差范围内。这也间接说明在相对恶劣的噪声条件下，在一定的误差范围内，本方法仍然可以保证多普勒频率估计和脱靶量估计的准确度。

4 结论

本文提出基于维特比算法的引信多普勒信号频率估计方法。该方法能够处理连续波体制无线电引信获得的多普勒回波信号，并利用改进的Viterbi方法提取其最佳时频特征点，然后按照多普勒信号的函数模型进行拟合分析，可得到多普勒信号关于时间和频率关系的函数估计和脱靶量的参数估计。仿真实验结果表明，在信号中具有较强的噪声干扰的情况下，本文方法得到的脱靶量估计值与真值的偏差仍在可接受的误差范围内，间接证明了本文提出的基于维特比算法的引信多普勒信号频率估计方法具备一定的准确性和抗噪声能力，是对现有相关试验测试手段和数据处理方法的有效补充，具有一定的参考借鉴意义。