引信可靠度置信度指标转换及对应抽样检验方案

刘小岗，冯爱国

(西安机电信息技术研究所，陕西 西安 710065)

0 引言

引信是弹药的重要部件，其作用可靠性直接影响着武器系统的效能。引信产品的可靠性指标，是指引信产品可靠性的定量要求[1]，是评价引信可靠性是否达到要求的依据。研究引信可靠性及其考核方法对提高引信系统的可靠性设计水平具有重要的意义。多年来，引信可靠性水平在逐步提高，但与可靠性联系极为紧密的引信可靠性指标及抽样检验等方面的问题仍然很多，指标五花八门，理解千差万别，最后导致抽样检验方案差异悬殊，严重影响了科研生产活动。因此，需要准确理解概念内涵，从根本上解决问题。

文献[2]及文献[3]相继论述了生产及使用方多年来对引信“可靠度-置信度”形式的可靠性指标理解上存在的偏差，但应用效果仍不明显，不少科研人员和军事代表仍然对引信可靠性指标及抽样检验的相关概念理解有误，导致在鉴定、验收等诸多环节产生较多分歧。因而有必要对引信可靠性指标存在问题进行分析，完善指标并明确兼顾双方利益的抽样检验方案和流程。本文针对由引信“可靠度-置信度”形式的可靠性指标及抽样检验引出的诸多问题，提出了引信可靠度-置信度指标转换及对应抽样检验方案。

1 引信的抽样检验

在讨论引信可靠性指标之前，有必要先讨论一下引信的抽样检验，因为引信各种形式的可靠性指标均涉及抽样检验的数理统计基础。

对于全数检验，标准唯一，可按照规定的质量标准进行检验，满足指标则通过，不满足则拒绝，即首先规定产品批不合格品率P0来作为判断标准，当P≤P0时，产品批为合格，接收概率Pa(p)=1；当P>P0时，产品批为不合格，Pa(p) =0。全数检验的操作特性曲线(OC曲线)如图1所示，是理想的OC曲线，可作为评价抽样方案优劣的依据。

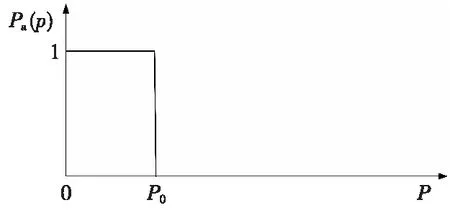
图1 全数检验OC曲线Fig.1 OC curve of full inspection

引信是一次性使用产品，一般只能采用抽样检验的方式来考核可靠性，即用样本的质量状况去估计总体的质量水平。以样本量n、接收数c的抽样方案(n,c)对批产品的接收概率Pa(p)可根据二项分布[4]近似计算：

(1)

式(1)中，p为总体失效率，d为中间变量(0,1，…,c)。

更精确的计算可用超几何分布计算。批次失效率从0到1取值，得到对应的一组接收概率值Pa，即方案(n,c)的OC曲线，如图2所示。失效率P0定义为合格标准AQL，失效率P1定义为拒收标准LTPD，α为误判拒收概率，(1-α)为置信度，β为误判接收概率。可见，与全数检验OC曲线相比，抽样检验仅能做到失效率小于等于P0高概率接收，失效率大于P1高概率拒收。P0～P1属于“灰色地带”，这是由抽样的本质决定的，点(P0, 1-α)和(P1,β)决定OC曲线的鉴别力。产品全部检验完，P0、P1才能重合为一点，如图1所示。

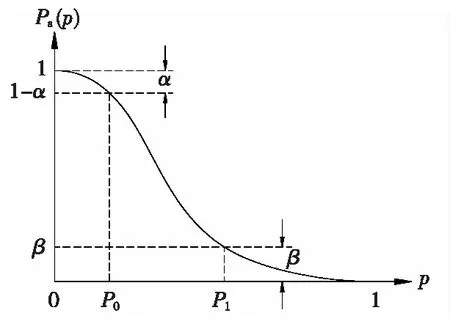
图2 抽样检验OC曲线及供需双方的风险Fig.2 Sample OC curve and the risks of both parties

OC曲线虽然不能精确地探知批次的不良率，但是它能够确定不同不良率下的接受概率。在实际检验中，提交批的质量水平是不知道的，OC曲线形象地显示了在任一质量水平(不合格品百分数)下批被接收的概率。

如果需要确定α和β风险，可根据下式计算样本量n和接收数c(先给定PAQL和PLTPD)。

(2)

(3)

GB/T 4087[4]就是根据二项分布计算拒止置信水平γ(γ=1-β)下的可靠度置信下限RL(RL=1-P1)。β是对应PLTPD的小接收概率，RL自然为拒收标准，即“不可容忍的最好水平”。

下面以某考试录取规则为例对应说明OC曲线各参数的意义。受条件所限并提高效率，先预考，再正式考试。假设满分700分，预考的分数线为400分，之后正式考试录取线为500分。过半考生可以通过预考，但意义不是很大，因为离真正录取线还有一段距离。这里的400分就是(1-P1),目的是为了淘汰差生，但也不能排除差生运气好考出较高分数，这个风险就是β。同理，这里的500分就是(1-P0)是合格标准，但也不能绝对排除好学生发挥失常，这个风险就是α。可以看出，录取线500分的实际意义要远大于淘汰线400分。大家普遍存在的误解就相当于把淘汰线当做录取线，而且对较高淘汰线的杀伤力感受不深，对录取的考生考了多少分也不十分清楚。

2 引信可靠度置信度指标转换及抽样方案

2.1 引信可靠性指标

过去，引信的可靠性指标多表述为失效率不大于n/N，n为失效数，N为试验总数(累积数理一般40～50)。在科研阶段，不涉及抽样，置信度就是1。该形式指标简单易考核，与可靠性指标的实际内涵相对接近，实际应用效果要好于“可靠度-置信度(RL，γ)”。具体的验收方案可在产品规范中根据可靠性指标和GJB179A[5]详细说明。

GJB1909.9[6]明确弹药、火工品的可靠性参数可选用成功率，即产品在规定的条件下完成规定功能的概率或试验成功的概率。GJBz20119[7]首次将“可靠度-置信度”概念引入引信行业，但这里的“可靠度-置信度”是根据二项分布计算的(RL，γ)，单侧置信下限RL对应抽样方案OC曲线的(1-P1)，是拒收标准，到底可靠性达到什么程度才能被大概率接收没有明确。被大概率接收的可靠度就是“可靠度-置信度(1-RAQL，1-α)”概念。

可靠性指标(1-RAQL，1-α)中，(1-RAQL)体现批产品的质量水平，是合格的标准，可作为接收指标，即产品的主要可靠性指标。RL、(1-RAQL)均指成功率，但一个是拒收，一个是接收。完整的指标应该包含正反两方面的要求。

GJBz20119-1993提出“中大口径地炮榴弹触发引信，在各种条件下，对中等硬度地面射击，置信度 0.90，作用可靠度不小于 0.92”等指标要求，该指标实质上是利用抽样数据估计总体中合格品率的单侧置信下限RL，即总体中合格品率在0.92～1之间的置信度是0.90，或有90%的把握认为总体中的合格品率不小于0.92。

应当说明，可靠度-置信度(RL，γ)指标中，RL是参数区间估计的单侧置信下限，可靠度为RL的产品批，是要高概率拒收的。如指标为(0.94，0.9)，则可靠度为0.94的产品批，通过的概率只有0.1，如图2中的P1。因而，对引信来说，可靠度-置信度(RL，γ)指标形式的可靠性指标(0.94，0.9)是很高的要求，按照GB/T 4087查出的“验收方案”可以在小样本量情况下保证使用方的风险，但产品的可靠性要远大于(1-RAQ)才能以对等的风险被接收。因而，完善的指标应该包含接收、拒收成功率和各自的风险，引信行业一般规定α=β=0.1，接收、拒收成功率可根据产品特点与用户约定。

2.2 指标转换

综合以上分析，把引信的可靠性指标定义为“可靠度-置信度(RL，γ)”的形式是对可靠性指标的误解，其应用效果还不如“失效率不大于n/N”指标的要求明确，引信可靠性设计指标可以采用“失效率不大于n/N”的简单形式(本质也是成功率，是接收标准)，更规范的形式可以根据实际要求采用“可靠度-置信度(1-RAQL，1-α)”的形式，同时给出约束条件(RL，γ)。

但目前的可靠性指际仅给出“可靠度-置信度”，其实质是(RL，γ)，应用中必然出现歧义。引用文献[3]的例子，对于(0.93，0.9)的指标，按(RL，γ)的概念理解，抽样方案可选(54,1)，而按(1-RAQL，1-α)的概念理解，抽样方案可选(16,2)，差异巨大。实际上，指标形式应该按照可靠性的内涵理解成(1-RAQL，1-α)的形式，但(16,2)的抽样方案与用户的期望差距较大。直接按数值选方案，会降低产品的质量标准。

已有“可靠度-置信度(RL，γ)”指标可结合产品的实际可靠性要求转换成“可靠度-置信度(1-RAQL，1-α)”的形式，(RL，γ)作为累计考核指标，以保证使用方的利益。可在目标值的基础上确定RAQL，再换成(1-RAQL，1-α)的形式。本例可根据产品(RL，γ)指标，查GJB179A大样本量对应的(1-RAQL，1-α)形式的指标为(0.975，0.9)，即0.975是接收标准，即“可容忍的最差水平”。

2.3 抽样方案

对于逐批连续生产抽样检验，抽样方案应优先考虑保护生产方，即首先保证(1-RAQL，1-α)指标，使用方的风险可通过连续批累加考核保证，这是由抽样固有的风险和交验检验共同决定的。一次抽样方案是实际中应用最广的抽样方案，核心是样本量。(0 1)方案(0为过，1为不过，下同)样本量少，但生产和使用双方的风险都大，应尽量避免，按照这样的方案通过与否说服力都不强。(1 2)方案可以兼顾风险和成本，尤其是高价值弹药引信。生产方应克服困难，尽量增加样本量。科研阶段的样本量可以采取相同技术状态产品累加的数据处理方式。生产阶段可以累积考核，以更准确探知产品的真实质量水平。

如对于原指标(0.94，0.9)，按照(1-RAQL，1-α)理解，抽样方案为(10，1)或(19，2)，可靠性要求偏低。按照(RL，γ)查GJB179A表6，对应抽样方案为(200，7)时，接收与拒收的风险均可接受(α=β=0.1)，对应的质量水平也代表了目前对引信可靠性的要求，抽样方案(200，7)对应的(1-RAQL，1-α)指标(0.985，0.9)是合理的，但如此大的样本量对高价值弹药引信已经失去了抽样检验的意义。

下面以(RL，γ)形式指标(0.94，0.9)为例对比说明相关指标内涵及抽样方案差异，见表1。(1-RAQL，1-α)为直接形式对应的接收指标，α=0.1。转换(1-RAQL，1-α)即为(RL，γ)形式指标对应的大样本量条件下α=0.1时的可接收成功率。

表1 各指标形式一次抽样方案对比(α=β=0.1)

由表1可见，(RL，γ)形式指标对应的一次抽样方案均对使用方有保证，生产方的风险大，产品的可靠性要超过应有的指标才能大概率通过；直接形式对应的(1-RAQL，1-α)接收指标一次抽样方案生产方易通过，使用方的风险大，也不是使用方的本意；转换(1-RAQL，1-α)形式指标对应的(1 2)方案对接收成功率、拒收成功率均有考虑，最多经6批检验合格，累计样本量达到200，可使α、β风险均可控制在0.1以内。从(0 1)方案与(1 2)方案的对比也可以看出样本量在抽样检验中的重要地位，产品指标应以(1-RAQL)为主，以RL兜底。

3 抽样检验相关问题

3.1 多次抽样方案

对于(RL，γ)形式指标，一次抽样(0 1)方案样本量少，但通过风险大，二次抽样方案可以减小通过的风险吗？实际上，一次抽样的OC曲线与二次抽样、七次抽样的OC曲线非常接近，在GJB179A中也仅给出了一次抽样的OC曲线，其风险差异可忽略。二次抽样必须要有对应的一次抽样方案(非零方案)，先提高样本量，而且第一样本数量与一次抽样方(0 1)案接近，如果出现失效数，第二样本会非常严格。一次抽样(0 1)方案对数据的积累贡献小，生产和使用双方的风险都大。同理，七次抽样方案也不会降低通过风险，而且由于七次抽样方案程序复杂，操作繁琐，还未见有实用。

3.2 对抽样检验的几点建议

对于样本量很少的高价值弹药引信，即使置信度0.8的情况下样本量也难以达到，应采信同状态的试验数据或其他数据，同时要注重连续批数据积累。

数量大于50的样本量已经是大样本量，这种情况下更能反映产品的真实质量水平，建议自检与军检合并检验。如两次检验均按(30，1)的方案抽样，对应指标(0.982，0.9)，还不如一次(50，1)的抽样方案，对应指标(0.989，0.9)更有说服力。同一批产品重复检验没有理论依据，浪费严重，应加强过程监督，制定合理标准，注重多批次累计考核。

4 结论

本文针对引信“可靠度-置信度(RL，γ)”形式的可靠性指标及抽样检验方案在概念理解上存在的偏差，提出了引信可靠度-置信度指标转换及对应抽样检验方案，转换指标对原指标按照大样本量对应的可接收成功率转换成“可靠度-置信度(1-RAQL，1-α)”形式，明确了符合可靠性定义要求的可接收成功率指标。与转换指标对应的一次抽样(1 2)方案及流程可以保证(1-RAQL，1-α)指标，使用方的风险可通过连续几批累加保证，从而使α、β风险均控制在可接收的范围内。