基于多区域采样策略的混合粒子群优化求解多目标柔性作业车间调度问题

张闻强，邢 征，杨卫东1，

（1.粮食信息处理与控制教育部重点实验室（河南工业大学），郑州 450001；2.河南工业大学信息科学与工程学院，郑州 450001）

0 引言

现代化制造业所涉及的供应及制造流程正日益数据化、智慧化，快速、有效、个性化的生产模式开始成为主流。在此趋势下，制造企业生产车间的灵活性面临着严峻的挑战［1］。如何合理地调度车间生产任务，使加工时间和加工成本最小化，是制约现代化制造企业发展的重要因素。其中，车间调度是指作业车间在生产能力和生产资源有限的前提下，依据被加工工件的工艺规程以及相关的约束条件，规划出多个工件各工序间最优的加工顺序组合方案，来使生产系统的综合性能达到最佳。在车间调度优化问题的研究中，多目标柔性作业车间调度问题（Multi-Objective Flexible Job-shop Scheduling Problem，MOFJSP）是最困难也最接近实际生产环境的车间调度优化问题［2］。

现有的调度优化算法一般分为两类：精确算法和启发式算法［3］。精确算法虽然具有较高的收敛速率，但算法的灵活性较差，且求解过程相对繁琐，需要使用优化问题的梯度信息。对于柔性作业车间调度问题（Flexible Job-shop Scheduling Problem，FJSP）这 类 典 型 的NP-Hard（Nondeterministic Polynomial Hard）问题［4］，最合适的优化技术是启发式算法。关于这些启发式方法的研究属于进化算法（Evolutionary Algorithm，EA）领域［5-6］。EA是一类成熟的具有高鲁棒性和广泛适用性的全局优化方法，能够不受问题性质的限制，有效地处理传统优化算法难以解决的复杂问题。而且由于这些算法对种群中的大量潜在的解决方案进行操作，因此可以更有效和高效地探索大型和崎岖的搜索空间。

对于一个EA，如果希望保证算法可以较快地找到符合期望的近似最优解，那么就必须保证算法在探索和开发之间达到合理的平衡。然而，基于无免费午餐定理［7］，没有任何单一的搜索方法可以保证完美地解决所有可能的问题，特别是多目标优化问题（Multi-objective Optimization Problem，MOP）。由于MOP的复杂性，固定的单一策略在解决这类复杂问题时可能会遇到一些困难。因此，合理地兼顾收敛与分布，是打破单一进化策略解决MOP固有局限性的好方法［8］。同时，根据每个算法的特点混合不同的进化算法，可以发挥各种算法的优势从而得到更好的算法改进［9］。

近年来，关于求解MOFJSP的研究相当地活跃，已有许多有效的算法被应用于解决该问题。李俊青等［10］提出了一种基于Pareto档案集的混合禁忌搜索（Tabu Search，TS）算法。其中，混合TS算法将Pareto非支配排序算子应用于邻域解集，并包含一种加速Pareto集更新算法。同时，为了减小搜索空间，为算法设计了特殊的插入邻域和交换邻域算子。文献［11］针对三个目标的MOFJSP开发了一种混合蛙跳算法。所提的混合蛙跳算法使用了一种改良的种群初始化方法，采用自适应策略来为种群中的个体分配非支配解，并在算法中嵌入了几种局部搜索方法用以拓展算法在后期的搜索能力。孟冠军等［12］将TS算法与改进的人工蜂群（Artificial Bee Colony，ABC）算法混合来解决MOFJSP。其中主要的改进之处在于，在ABC算法的不同阶段采用不同的搜索机制，有效提升了获得最优解的概率。张丽［13］提出了一种混合多目标优化算法。改进算法将NSGA-Ⅱ（Non-dominated Sorting Genetic AlgorithmⅡ）算法与粒子群优化（Particle Swarm Optimization，PSO）算法相融合，并对参数进行有效优化，防止算法陷入局部最优；同时修改了精英选择策略，考虑删除个体后对邻域个体拥挤密度的影响，将原本被删除的较优个体予以保留，以提高种群整体的质量。张立果等［14］针对大多数算法解决MOFJSP所存在无法在单一目标进行深度搜索的问题，提出了一种求解多目标问题的双层遗传算法。改进算法舍去了遗传算法中的选择算子，并采用了一种新的交叉策略，以牺牲部分收敛速率的代价充分地提高了种群的多样性。

使用PSO来解决MOFJSP的研究也有很多。Huang等［15］将PSO与变邻域搜索算法相结合来解决MOFJSP。该算法的种群初始化方法为先由分配规则和调度规则产生优良个体，然后由所设计的基于最早完成机（Earliest Completion Machine，ECM）机制的交叉和变异算子来进行扰动以产生新的个体。变邻域搜索主要应用于优化全局历史最优解的分布，以增强算法的本地搜索能力。Kamble等［16］将粒子群算法与模拟退火（Simulated Annealing，SA）混合提出了混合算法（PSO-SA）。该算法创新地利用Pareto前沿和拥挤距离来确定粒子的适应度，并使用PSO来实现良好的全局搜索能力。在实现高效收敛的同时，结合SA算子来进行局部搜索，以赋予算法避免陷入局部最优的能力。文献［17］中描述了一种混合粒子群优化算法，采用基于作业工序和机器分配的粒子表示方法，在离散域中直接更新粒子。该算法中混合使用了鲍德温学习机制和SA来平衡全局搜索和局部搜索，并使用Pareto优势度来更新外部存档中的历史最优个体。王云等［18］将密集距离排序方法融入PSO中，同时使用精英保留策略保存进化过程中的优势个体，基于个体密集距离降序排列进行外部种群的缩减和全局最优值的更新，并引入变异机制以增强种群的多样性和算法的全局搜索能力。仲于江等［19］尝试利用PSO算法获得存储非劣解的外部存档，再基于小生境技术计算粒子的删除概率对其进行更新，并在最终解集的处理上提出了一种总体价值估计选取方法，以便于从最终解集中确定符合需求的折中解。毛天晔［20］改进了PSO的进化方式，通过使用三种不同的途径移动算子来保证工序序列向量和机器分配向量间的协同进化，并提出一种动态判断种群停滞的机制，将PSO算法和TS算法有效结合；此外，改进算法还使用了基于关键路径的禁忌邻域结构，这收缩了邻域空间的大小，提高了邻域搜索的效率。尉雅晨［21］提出了独立自适应参数调整的PSO算法。改进算法使用了惯性权重及学习因子的独立调整策略，以动态优化算法参数；同时，改进算法中以粒子的适应度值和进化能力作为指标对种群进行采样划分，并根据子种群的特性分别采用粒子重构策略和差分变异策略两种不同的操作更新粒子。

虽然目前关于解决MOFJSP已有了较多的研究，但多数研究仅针对算法进行改进，较少有研究者考虑针对问题特点改进算法的相关策略；因此本文提出了基于多区域采样策略的混合粒子群优化算法（Hybrid Particle Swarm Optimization algorithm with Multi-Region Sampling strategy，HPSO-MRS）。HPSO-MRS的主要特点是：在问题层面上，针对FJSP设计了相应的带插空机制的解码策略和基于邻域差异的交叉算子，增强算法的问题搜索能力；在算法层面上，为了增强多目标PSO中趋近Pareto前沿面多个区域的强收敛能力，设计了多区域采样（Multi-Region Sampling，MRS）策略，有针对性地调整粒子在多个方向上的收敛能力，并带来一定程度上均匀分布能力的提升。同时，由于HPSO-MRS的算法框架中并未设定特殊的个体拥挤距离计算和维持机制，一定程度上降低了计算时间，并依靠多方向强收敛带来一定的分布性能维持能力。

1 FJSP描述

FJSP的主要特点是，要在某个作业车间中加工一批工件，每个工件由一组工序集合构成，这些工序遵循顺序约束，即第一个工序未完成时第二个工序无法开始；同时，每个工序对应一组具备加工能力的机器集合，机器具备不可抢占性和不可中断性。正因此特点，FJSP在求解时不仅要考虑确定作业路径，还需要确定每个工序对应的处理机器，其中涉及了大量的约束关系，因此该问题实际的求解过程相对复杂，在求解该问题的过程中很容易陷入局部最优。

为了清晰地描述所考虑的问题，使用以下的符号。

1）索引：

i，h为工件索引；i，h=1，2，…，n；

j为机器索引；j=1，2，…，m；

k，g为工件的工序顺序索引，k，g=1，2，…，ni；

v为机器上的工序顺序索引，v=1，2，…，mj。

2）参数：

n为工件总数；

m为机器总数；

ni为工件i的工序总数；

mj为机器j上处理的工序总数；

A（i，k）为工件i第k个工序的可用机器集合；

oik为工件i的第k个工序；

pikj为工件i的第k个工序在机器j上的加工时间；

wjv为机器j上第v个被加工的工序；

qvj为机器j上第v个被加工工序的加工时间。

3）决策变量：

cik=工序oik的完成时间；

tjv=wjv的完成时间

其中，参数mj、wjv和qvj是过渡参数。参数wjv与oik描述的均为某个工序，但oik可以在问题集中被找到，wjv则只能从具体解码出的调度时间表当中得知。同样地，参数mj和qvj也是一样的情况。根据符号，考虑的FJSP可以表述为：

目标函数（最小化）：

约束条件：

式（1）～（2）是最小化最大完工时间（Makespan，Cmax）和总机器延迟时间（Total Machine Delay Time，Td）的目标函数。在式（2）中，如果存在某个解决方案在机器j上只分配了一个工序，那么Td=tj1-q1j-0。如果机器j上没有分配工序，则Td=0。解空间由8条约束集来描述。在式（3）中，规定同一个作业中工序的先后顺序，oi(k-1)加工完成前oik无法启动。式（4）说明在处理某个工序时，应从工序的可用机器集合A（i，k）中选择且仅能选择一台机器用于加工oik。对于同时分配在同一台机器j上两个工序oik与ohg，如果oik在ohg之前到达，那么ohg的启动时间应大于等于oik的完成时间，如式（5）所述。当然，在式（6）中，如果ohg在oik之前到达，那么oik的启动时间同样应大于等于ohg的完成时间。同理，式（7）规定，在同一台机器j上分配的所有工序都应满足像式（5）和式（6）中的规则。式（8）中给出了机器选择决策变量的取值范围，式（9）～（10）规定了任意工序的完成时间均大于等于0。

2 基于多区域采样混合粒子群优化算法

2.1 HPSO-MRS

HPSO-MRS的总体结构如图1所示。其中初始化粒子群将在2.2节中描述；计算适应度值为分别计算粒子群中个体的式（1）与式（2）的数值；更新外部存档采用先将当前非支配解加入全局历史最优粒子（Gbest）集合与每个粒子的个体历史最优粒子（Pbest）集合，再从集合中去除所有被支配解的方法；多区域采样策略将在2.3节中展开；更新粒子位置的方法将在2.4节中描述。更为详细的过程在算法1中给出。

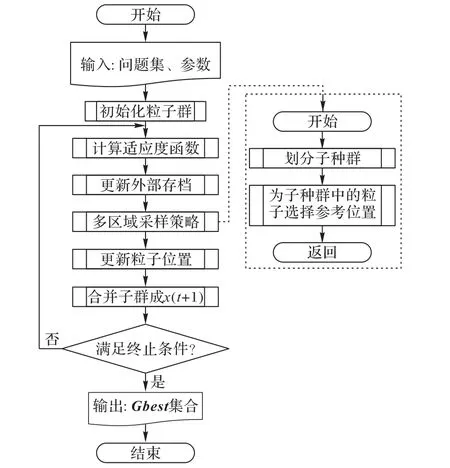
图1 HPSO-MRS总体结构Fig.1 Overall structure of HPSO-MRS

算法1 HPSO-MRS。

输入：问题数据，参数；

输出：全局搜索到的最优解集（Gbest集合）。

1）初始化粒子群（大小为N）；

2）while最大评价次数do

3）根据式（1）与式（2）计算每个粒子的适应度值；

4）将所有非支配粒子放入Gbest集合；

5）去除Gbest集合中的所有被支配解；

6）for每个粒子do

7） 将粒子放入该个体对应的Pbest集合；

8） 从该Pbest集合中移除所有被支配解；

9）end for

//多区域采样策略（MRS）

10）粒子群中的所有粒子根据式（1）的数值排序并根据Fit1的子种群规模选取粒子；

11）所有粒子根据PDDR-FF函数数值排序并根据PDDR的子种群规模选取粒子；

12）所有粒子根据式（2）的数值排序并根据Fit2的子种群规模选取粒子；

13）for子种群Fit1中的每个粒子do

14）采用二元竞赛选择法，根据适应度函数（1）的值对Pbest和Gbest进行选择，并更新粒子位置；

15）end for

16）for子种群PDDR中的每个粒子do

17）采用二元竞赛选择法随机Pbest和Gbest进行选择，并更新粒子位置；

18）end for

19）for子种群Fit2中的每个粒子do

20）采用二元竞赛选择法，根据适应度函数（2）的值对Pbest和Gbest进行选择，并更新粒子位置；

21）end for

22）所有子种群合并成重组粒子群（大小为N）；

23）end while

24）returnGbest集合；

2.2 编解码与粒子初始化

本文采用两段编码，分别是工序分配（Operation Assignment，OA）决策变量和机器选择（Machine Selection，MS）决策变量。表1中给出一个4×4的FJSP示例。

表1 FJSP示例Tab.1 FJSP instance

根据示例与编码规则可有如下编码，如图2中的OA与MS序列所示。OA序列分别是每个作业中工序的排序，作业中有几个工序，作业序号就重复出现几次，首次出现的相同作业序号代表该作业的第一个工序，第二次出现即代表该作业的第二个工序。OA序列的数值顺序敏感，任意交换两个位置的数值可能会影响其他位置数值的释义。初始化粒子时，通过扰乱一条合法的OA序列中等位基因的排序来产生新的序列。MS序列分别是从J1到J4的每个工序的机器选择决策变量，变量数值为该工序对应所有可加工机器列表的下标。另外，MS序列的数值不具备顺序关系。初始化粒子时，MS序列中的每一位数字从该工序对应的可加工机器列表的下标中随机产生。

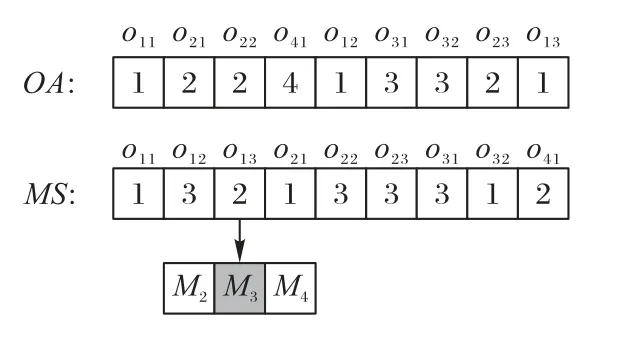
图2 编解码示例Fig.2 Encodingand decoding instance

解码时，先读取一位OA，根据该序号对应的作业序号以及该序号是第几次出现确定这位基因对应的是哪个工序。再由MS序列对应这个工序的决策变量决定这个工序所在的处理机器。释义结果如图3所示。在生成时间表时，如果使用常规解码策略解码，如OA的第一位为1，MS的第1位为1，则o11要在机器M1上加工，处理时间为1；OA第二位为2，MS的第4位为1，则o21要在机器M2上加工，处理时间为4。以该规则解码的甘特图如图3上半部所示，在该方案中，最大完工时间为14，总机器延迟时间为22。

图3 带插空机制的解码方法Fig.3 Decoding method with interpolation mechanism

由于FJSP需要针对每个工件的单个工序来确定具体的作业路径，故而调度的结果中可能包含部分局部左移。因此针对这种问题，在解码方法中添加了插空机制。带插空机制的解码策略在遵循OA序列决定的工序顺序的同时，如果某个工序已被调度需要加入时间表，则判断调度时间表当中对应机器的所有空闲时间段。如果某个空闲时间段满足这个工序开始加工的所有约束，并且满足加工的处理时间长度，则在这段空闲时间段中放置工序，否则将该工序按照约束关系添加至该机器加工队列的队尾。针对同一段编码，带插空机制的解码策略调度产生的甘特图如图3下半部所示。由于机器M4的空闲时间段（1-4）满足o12开始加工的所有约束，所以o12工序可以被提前到o22工序之前完成。同样地，工序o13、o31、o32均可以被提前处理。在带插空机制的解码策略解码出的甘特图中，最大完工时间为11，总机器延迟时间为14。

通过对比两种解码方法的甘特图和两个目标函数值可知，针对完全相同的粒子编码序列，带插空机制的解码方法可以得到更好的调度方案。在第3章的实验部分，为了得到合理的对比结果，所有的算法均采用改进的解码策略。

2.3 多区域采样策略

由于本文所考虑的MOFJSP同时最小化两个优化目标，因此在问题求解过程中会存在许多非支配解，故而在考虑算法最终结果收敛性的同时，也需要注重分布性能。

本文使用基于Pareto支配和被支配关系的适应度函数（Pareto Dominance and Dominated Relationship Fitness Function，PDDR-FF）来筛选种群中的非支配个体［22］。PDDRFF函数的计算过程如式（11）所述：

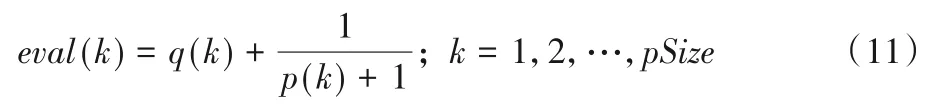
其中：q（k）是粒子群中支配粒子k的粒子个数，p（k）是粒子k支配粒子群中其他粒子的个数，pSize是粒子群中粒子的个数。较小的eval（k）说明粒子k在当前粒子群中拥有较好的收敛性，据此可以区分出种群中较为靠近Pareto的个体粒子。同时，矢量评估遗传算法（Vector Evaluated Genetic Algorithm，VEGA）在解决多目标优化问题时，选择将个体分别在不同的单个目标上进行优化，因此VEGA具备着优良的分布性能。

MRS策略综合了上述函数和算法的优点，将粒子群中的粒子根据自身所在的优势区域加以区分，并指导这些粒子在自己的优势方向上继续移动。如图4所示，在PSO中，通过添加特定的选择策略分别选择出靠近Pareto中心和两个边缘区域的粒子，让靠近Pareto中心区域的粒子继续向中心区域移动，靠近Pareto的两个边缘区域的粒子继续向两个边缘区域移动，从而在确保算法的收敛性能的同时保证分布性能。让粒子向特定方向的移动，是通过粒子在更新位置时，为粒子选择在这些方向上较好的Pbest和Gbest来实现的，如图5所示。

图4 粒子划分示意图Fig.4 Schematic diagram of particle partition

图5 子种群粒子更新示意图Fig.5 Schematic diagram of subpopulation particleupdate

适应度函数f1与f2指的是本文所解决的MOFJSP中最小化的两个目标函数。划分子种群时，根据VEGA的思想，靠近Pareto上边缘区域的粒子在适应度函数f1（式（1））上会具有较小的数值，因此可以根据适应度函数值f1的数值大小来选择靠近Pareto上边缘区域的子种群（Fit1）中的粒子。同样地，靠近Pareto下边缘区域的粒子会具有较小的适应度值f2（式（2）），根据适应度值f2的数值大小来选择该方向上子种群（Fit2）中的粒子。根据PDDR-FF的思想，如果当前种群中某个粒子被支配的数量越少、支配其他粒子的数量越多，PDDRFF数值就越小，相对整个粒子群而言也就越靠近Pareto中心区域。因此靠近Pareto中心区域的子种群（PDDR）中的粒子根据PDDR-FF指标的数值大小来选择。此外，分别划分三个子种群的操作流程均是将粒子群中的所有粒子按照不同的数值依据进行排序，并根据预设的子种群大小从排序的结果中依序取得。

选择参考位置时，均采用二元竞赛选择法从参考位置集合中选取。对于Fit1中的粒子，选择Gbest时根据规则，从全局的Gbest集合中随机选择两个个体，将函数值f1更小的一个作为本次更新所参考的Gbest；选择Pbest时，从被更新粒子个体的Pbest集合中随机选择两个个体，将函数值f1更小的作为本次更新所参考的Pbest。Fit2中的粒子采用同样的方法来选择参考位置，但竞赛胜出的规则改为适应度值f2更小。对于PDDR中的粒子，由于全局的Gbest集合以及被更新粒子对应的Pbest集合中存储的都是非支配解，无法根据PDDR-FF函数加以区分，因此随机选择任意一个即可。

本文第3章中参与比较的HPSO不具备划分子种群的操作，同时HPSO中对于参考位置的选择均是随机选择。

2.4 粒子更新方式

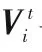
由式（11）～（12）可知，在经典PSO算法中，粒子的移动主要受到自身惯性、Pbest以及Gbest三部分的指导，但加速度的表达使得经典PSO在解决离散的组合优化问题时变得困难。为了使PSO可以更好地处理MOFJSP，本文混合了遗传算法的交叉和变异算子来更新粒子位置［23］。HPSO-MRS的粒子更新公式如式（14）所述。其中使用的F1为一种基于邻域差异的交叉操作。F2是变异操作。

对应经典PSO的三部分指导，HPSO也由两个交叉算子以及一个变异算子来更新粒子位置。操作的流程由如下三个部分构成。

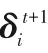
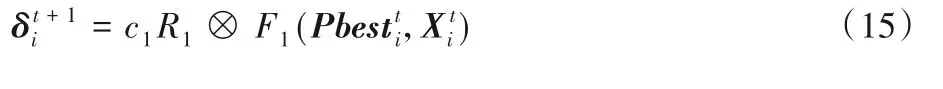
第二部分为等式（16），是该粒子的“社会”部分，代表粒子之间的协作。其中λit+1是中间粒子。

最后，第三部分为一个概率为ω的变异操作，如等式（17），代表粒子本身的突变，为搜索过程提供扰动。

交叉算子即等式（14）～（16）中的函数F1。由于粒子编码中的OA与MS序列结构的不同，交叉算子对这两部分的操作也不同，OA部分的交叉应注重避免非法解的产生。

OA序列交叉前需要寻找与参考位置间的差异。具体的操作流程在图6中给出。从当前位置OA序列的第一个等位基因出发，对比参考位置的第一位等位基因，如果不同，则在当前位置的OA序列中从第二位开始向后查找与参考位置内容相同的等位基因。找到后，将当前位置OA序列中的第一位等位基因与找到的等位基因进行交换，并记录这个交换所涉及的两个下标，如表2所示。另外，当前位置的等位基因与参考位置的等位基因携带的信息相同时，则参考位置不需要执行邻域动作。

图6 OA部分邻域差异获取示意图Fig.6 Schematic diagram of OA neighborhood difference acquisition

表2 获取的邻域动作Tab.2 Acquired neighborhood actions

在该过程中所找到的所有邻域动作可以视为当前位置到参考位置的总距离，按照一定的步长去执行这些邻域动作则可以视作当前位置向参考位置的移动。假设本次交叉的步长参数c1=0.5，随机数R1=0.8，则本次更新执行的步长为2，故选择的邻域动作即表2中的（1，3），（4，7），执行交叉的过程及结果则如图7所示。

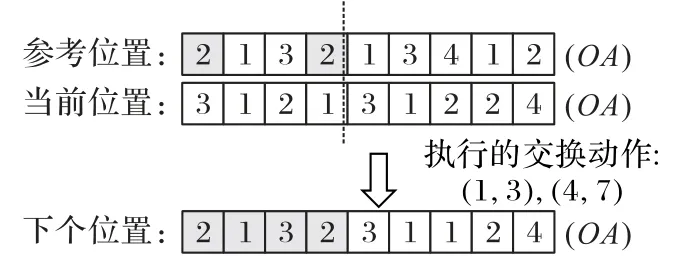
图7 OA部分交叉示意图Fig.7 Schematic diagram of OA crossover operation

MS序列交叉时，从参考粒子的MS序列中随机选择一位等位基因，然后将当前粒子的MS序列中相同位置的内容更改为所选择的等位基因。重复执行这个操作，直到满足本次交叉的最大操作次数。操作的次数由OA序列执行邻域动作的步长确定。由于本次交叉的示例中使用的步长为2，故MS序列交叉的结果如图8所示。

图8 MS部分交叉操作示意图Fig.8 Schematic diagram of MS crossover operation

变异算子即式（13）与式（16）中的函数F2。在决定是否进行变异操作时，随机产生一个［0，1］的任意实数，如果小于ω，则执行变异，否则跳过该操作。该变异操作遵循随机性原则，具体的操作如图9所示。在当前位置的OA序列中，随机选择两个下标，交换两个下标对应位置中的内容。在MS序列中，随机挑选一位等位基因，将该位置的内容根据其对应操作的可用机器集合进行重新随机选择。

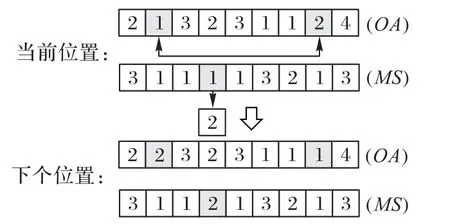
图9 OA及MS部分变异操作示意图Fig.9 Schematic diagram of OA and MS mutation operation

3 实验与结果分析

实验在Windows10系统下进行，CPU为Inter Core i5-4590CPU@3.30 GHz，内存为8 GB，实验环境是IntelliJ IDEA2019.2版本。数据集采用Benchmark问题Mk01～Mk10。对比算法分别为不包含MRS策略的经典多目标HPSO、基于非支配排序的经典多目标遗传算法NSGA-Ⅱ、基于适应度分配策略的多目标进化算法（Strength Pareto Evolutionary Algorithm 2，SPEA2）以及基于分解的多目标进化算法（Multi-Objective Evolutionary Algorithm based on Decomposition，MOEA/D）。所有对比算法与本文提出的改进算法HPSO-MRS均使用了2.2节中的改进解码策略与2.4节中的交叉变异算子。此外，在所有数据集上，每个算法各运行30次。

3.1 评价指标

本次实验分别使用评价指标HV（Hyper Volume）、IGD（Inverted Generational Distance）、Spacing来评估不同算法之间的解集质量。其中：

HV是解集中的个体所支配的空间大小。较大的HV指标值意味着更好的收敛性能。本实验中HV的参考点设定为在各目标上寻找到的最差的适应度值。

IGD是通过计算Pareto前沿到解集的距离得出的。当解集接近Pareto前沿时，较小的IGD指标值要求解集中个体的分布类似于Pareto前沿。越小的IGD指标值意味着更好的收敛性能和分布性能。

Spacing根据解集中每个解决方案与其他解决方案之间的最短距离来得出。较小的Spacing指标值意味着更好的分布性能。

因此，本次实验中主要使用指标HV和IGD来评估算法的收敛性能，使用指标Spacing来评估算法的分布性能。

3.2 实验结果

本次实验在10个Benchmark问题上进行测试，数据集是部分柔度FJSP，分别为Mk01～Mk10［24］。数据集的工件数量、机器数量以及工序对应的平均机器数如表3所示。

表3 数据集规模及差异Tab.3 Dataset sizeand difference

算法参数的配置情况如表4所示。所有算法的最大评价次数均设置为10 000，种群大小均为100，变异率均设置为0.2，随机步长范围均为0～1的任意实数。遗传算法的交叉率设置为0.8，步长设置为0.2。此外，HPSO-MRS与HPSO关于Pbest的步长设置为0.2，关于Gbest的步长设置为0.4。HPSO-MRS还需配置子种群大小，本次实验对于大小为100的种群将三个子种群的数量分别设置为30/40/30。

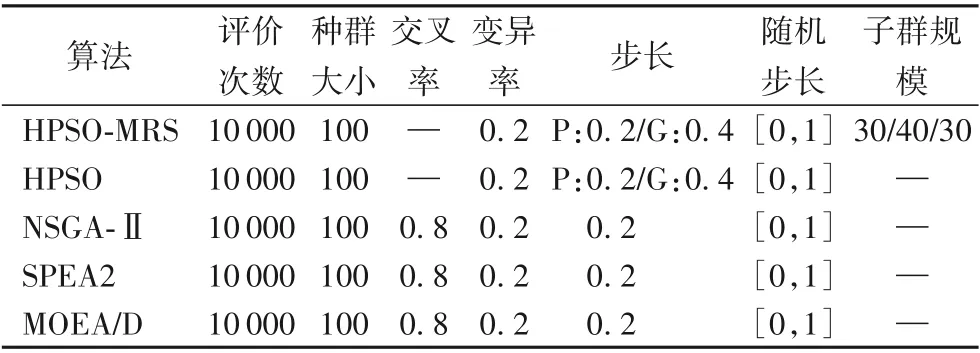
表4 不同算法的参数配置Tab.4 Parameter configuration of different algorithms

在算法效力方面，HV指标均值以及显著性分析结果在表5中展示，其中”+”“-”“*”分别意味着相对于HPSO-MRS，对比算法是显著性好、显著性差和结果相似（使用Wilcoxon’s rank sum test，0.05置信度下的结果，下同）。根据显著性分析结果可以看出，在85%的对照组中，HPSO-MRS均要显著优于其他四个对比算法，且30次结果的HV均值方面也均优于其他算法。因此，HPSO-MRS在多数情况下所搜索到的最终解集与参考点所构成的支配空间最大，故而HPSO-MRS相较于其他四个对比算法可以更稳定地获得收敛性更好的最终解集。

表5 HV指标均值及显著性分析结果Tab.5 Average HV and significanceanalysis results

表6中列举了30次运行结果IGD指标的各项分析结果。可以看出，除少数情况下无法确认优于其他对比算法的显著性，77.5%的对照组中HPSO-MRS仍旧显著优于对比算法。据此，结合五个算法的IGD指标均值，可以看出HPSO-MRS在多数情况下的最终解集最为靠近Pareto前沿、且分布情况更加接近于Pareto前沿面。

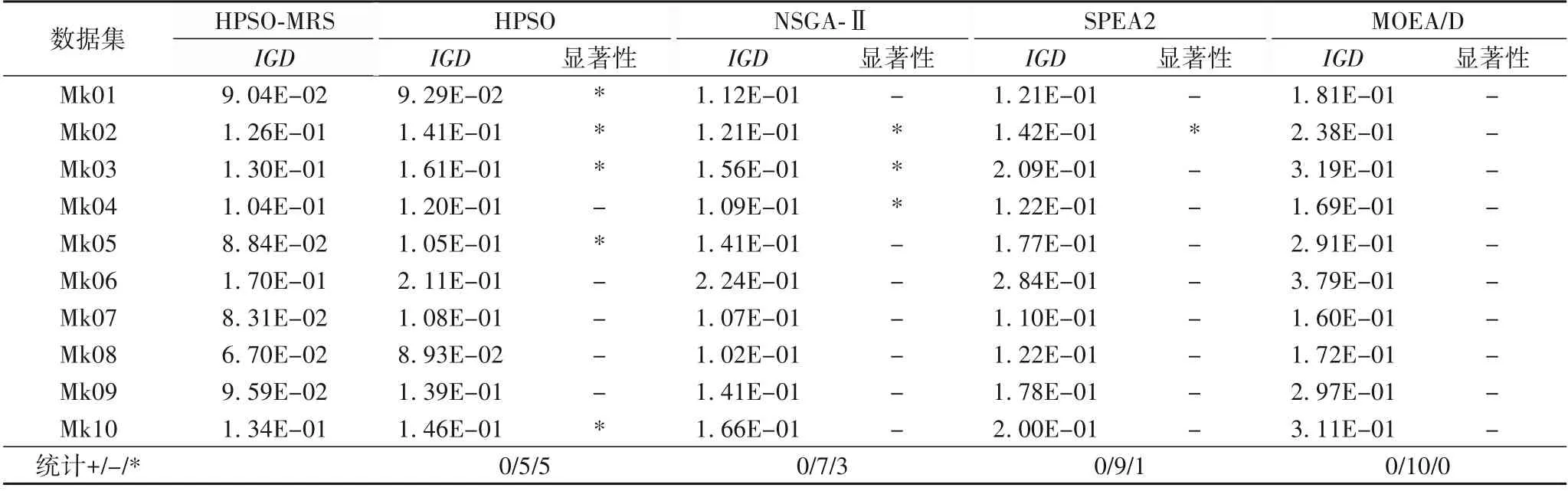
表6 IGD指标均值及显著性分析结果Tab.6 Average IGD and significanceanalysis results

Spacing的指标数据分析情况在表7中给出。在指标的显著性分析结果中，HPSO-MRS不具备显著优于HPSO的能力，但10个数据集下的指标均值多数优于HPSO。此外，HPSOMRS共在35%的对照组中显著优于对比算法，且其他四个对比算法均不存在显著优于HPSO-MRS的情况。因此，HPSOMRS的分布性能相较HPSO已经有所改善，且要优于其他三个对比算法。

表7 Spacing指标均值及显著性分析结果Tab.7 Average Spacing and significanceanalysis results

通过以上指标对算法的评估可以得出，在算法效力方面，由于MRS策略经过划分子种群与分别为不同子种群中的粒子选择参与指导粒子移动的参考粒子，从而增强了粒子趋近Pareto前沿面多个区域的强收敛能力，进而使HPSO-MRS整体具备较好的收敛能力。同时由于针对性调整了粒子在多个方向上的收敛能力，因此也带来一定程度的均匀分布能力的提升。

效率方面，表8中给出了每个算法的平均运行时间（CPU Time），单位为ms。通过算法30次运行的平均运行时间可以看出，HPSO-MRS与HPSO在解决较小规模的数据集时具备良好的运行效率，但随着问题复杂程度的提高，两个算法消耗的时间开始增加。特别是在Mk08～Mk10中，HPSO-MRS的运行时间高于其余四个对比算法。这是由于HPSO-MRS与HPSO算法为每个粒子都保留了一个单独的Pbest集合来保存搜索过程中粒子搜索到的所有非支配解，故而在解决非支配解较多的复杂问题时，个体的Pbest集合规模的不断扩大以及动态维护外部存档操作耗时的增加会使算法耗费较多的运行时间。同时，由于MRS策略的额外计算，HPSO-MRS总体的运行时间会略微高于HPSO，但HPSO-MRS中并未设定特殊的个体拥挤距离计算和维持机制，所以改进策略消耗的时间成本较低。基于无免费午餐定理，没有任何一个方法可以在完美解决所有类型优化问题的同时仍具备高效的运行效率，因此在算法中添加改进的优化策略往往导致运行时间成本的增加，本文提出的HPSO-MRS也是如此。综合HPSO-MRS算法在各个数据集上的效力优势及运行时间成本，可以确定HPSOMRS在算法时间方面的略微增加是可接受的。

表8 不同算法的平均运行时间 单位：msTab.8 Average running times of different algorithms unit：ms

4 结语

本文针对多目标柔性作业车间调度问题，提出了基于多区域采样策略的混合粒子群优化算法。该算法通过结合VEGA和PDDR-FF函数的优点，将粒子群中的个体粒子按照与Pareto前沿的位置关系进行划分重组，并为这些子种群中的粒子选择合适的参考粒子，以驱动它们继续在优势方向上移动。与其他算法相比，HPSO-MRS的收敛性能得到了较好的改善，同时分布性能也有了一定的提升。但该策略需要动态维护较多的外部存档，在解决较为复杂的问题时，随着数据集中非支配解数量的增加算法的运行效率可能会受到限制。下一步可将子种群划分的比例与搜索状态特征进行耦合，尝试在不同代数下根据粒子群中粒子分布的状态动态调整划分比例，以在保持收敛性能的前提下进一步提升整体的分布性能。同时，考虑在算法所动态维护的外部存档大小与问题所具有的非支配解数量之间达到平衡，以求在解决复杂数据集时，该策略仍可以拥有较好的运行效率。