基于二维Winograd算法的深流水线5×5卷积方法

黄程程，董霄霄，李 钊

（山东理工大学计算机科学与技术学院，山东淄博255049）

0 引言

卷积神经网络在图像分类、语音识别、目标检测等应用中取得了重大进展［1-3］。其中5×5卷积相较3×3卷积有更大的感受野，可以提取更多的边缘特征，在医学影像处理等领域效果显著，且广泛应用于AlexNet、ZFNet和GoogLeNet等经典模型［1］。近期的许多研究就使用包含5×5卷积的架构取得了较3×3卷积更高的预测准确率［4-6］。

卷积神经网络模型规模庞大，计算复杂度高，需要占用大量硬件资源，因此硬件加速器逐渐被用于加速神经网络的预测阶段。常用的神经网络加速器包括图形处理器（Graphic Processing Units，GPU）、专用集成电路（Application Specific Integrated Circuit，ASIC）和现场可编程逻辑门阵列（Field Programmable Gate Array，FPGA）。得益于高并行度、低能耗和可重构等优点，FPGA成为了目前主流的卷积神经网络硬件加速平台［7-16］。

目前在FPGA上加速卷积神经网络面临的问题有：1）卷积神经网络的大规模密集型计算受到FPGA计算能力（片上数字信号处理器（Digital Signal Processor，DSP）数目）的限制，如何优化算法以降低乘法运算量是提升加速器系统性能的主要问题。2）各类快速算法在降低卷积神经网络乘法运算量的同时通常以提升内存资源占用和存储器带宽占用为代价，FPGA片上硬件资源量的限制将影响加速器系统性能。3）卷积神经网络计算量庞大，高效的数据重用能够降低能耗开销并减小设计面积。

在5×5卷积的乘法运算量方面，文献［7］使用8 bit定点数据量化模型，在2个8 bit权重中插入1个8位的全0数据，组成一个低8位和高8位分别为权重数据、中8位为全0字段的24位新数据，使用1个DSP得出2次乘法运算结果，将传统卷积算法的乘法运算量降低至50.0%。文献［8］利用卷积的元素代数性质，应用Winograd快速卷积算法，将使用小尺寸卷积的VGGNet（Visual Geometry Group Network）等模型的乘法运算量降低至45.0%，有效提高了硬件加速器的效率。文献［9］基于二维快速傅里叶变换（Fast Fourier Transform，FFT）算法提出了一种灵活的自动化设计高通量模型加速器，将乘法运算量降低至约31.0%。文献［10］采用n=6的二维Winograd算法，级联3×3卷积构建5×5卷积，将乘法运算量降低至约19.4%。然而二维Winograd算法不同于传统卷积算法，使用级联3×3卷积的方法构建5×5卷积将增加乘法运算量、系统的存储器带宽需求，级联的卷积层间也存在计算延迟，同时也会增加设计空间探索周期。在硬件资源占用方面，文献［11］和文献［10］分别提出了基于列或行的二维Winograd卷积算法双缓冲区数据布局方案，降低了存储器带宽需求。然而文献［10］的研究结果表明，他们所设计的加速器存储器带宽占用比例略高于片上DSP占用比例，这意味着受制于有限的FPGA硬件资源，部分情况下其设计无法达到理论的最高性能。在数据重用方面，文献［12］提出了一种基于深流水线体系架构的二维/三维Winograd卷积算法加速器设计，通过层融合和层聚类等方法，显著提高了数据重用性。文献［11］和文献［10］通过双缓冲区数据布局方案重用了二维W inograd算法邻域间的重叠数据。但二维Winograd算法转换过程大量的加法运算中存在可复用的中间结果，这些可复用结果的加法运算属于无效运算，仅会增加加速器系统的能耗开销和设计面积，上述文献并未就此问题进行研究和优化。

针对上述方法中计算复杂度高、存储器带宽需求高、级联的卷积层间存在计算延迟、设计空间探索周期漫长和加法计算量大等问题，提出了一种基于二维Winograd算法的双缓冲区5×5卷积6级流水线方法。首先选用适宜尺寸的二维Winograd卷积算法降低计算复杂度和存储器带宽需求，然后通过双缓冲区最小块单元的设定指导并加快设计空间探索，增强可移植性，平衡FPGA硬件资源的使用，使设计不受任何硬件资源限制。最后通过深化二维Winograd卷积算法流水线，复用加法运算过程中的中间计算结果，来降低加法运算量，减小加速器系统的能耗开销和设计面积。

1 Winograd算法介绍

1.1 符号说明

表1对文章中使用的重要符号进行说明。

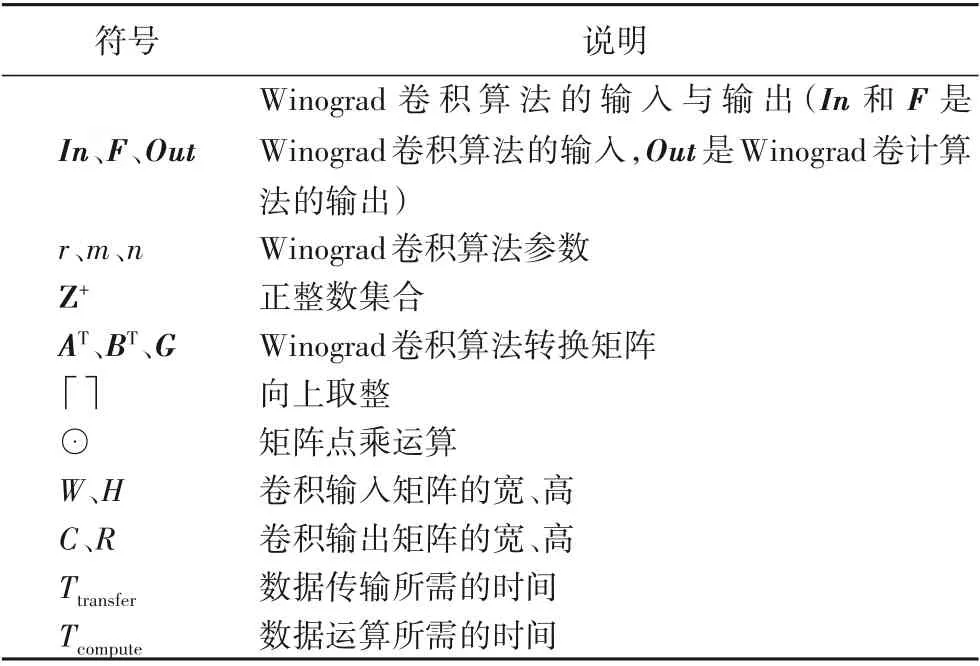
表1 符号说明Tab.1 Explanation of symbols

1.2 一维Winograd算法

Winograd算法于1980年由数学家Winograd提出［17］。以一维Winograd算法为例，记尺寸为r的卷积核输出m个计算结果为F(m，r)。

传统卷积算法计算F(2，3)需要2×3=6次乘法。Winograd算法计算F(2，3)仅需要4次乘法，输入输出如下：

具体过程如下：

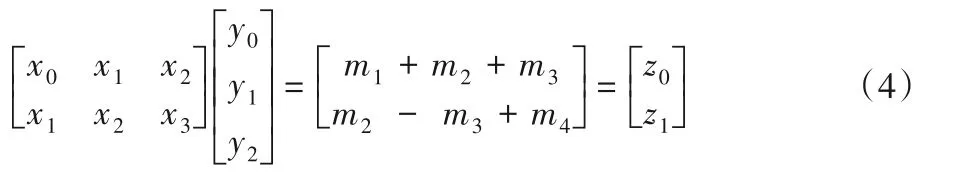
其中m1、m2、m3、m4为：

Winograd算法中的常数乘法可以通过移位操作（如2-1、2-2和2）或由2n或2-n（n∈Z+）的组合后再移位（如5=20+22，1/6≈2-3+2-5+2-6）近似得到，因而计算m1、m2、m3、m4只需要4次乘法运算。

上述乘法过程可表示为矩阵相乘形式：

其中Winograd算法F(22，32)的转换矩阵AT、BT和G表示如下：

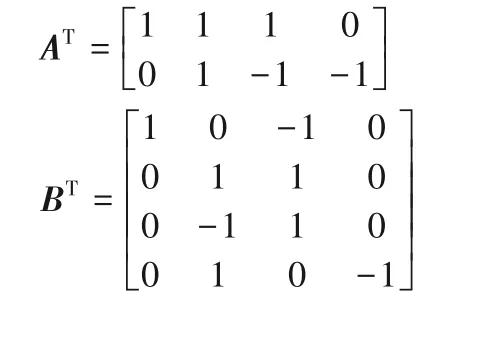
1.3 二维Winograd算法

F(m2，r2)的二维Winograd算法可以通过嵌套迭代一维Winograd算法得到：

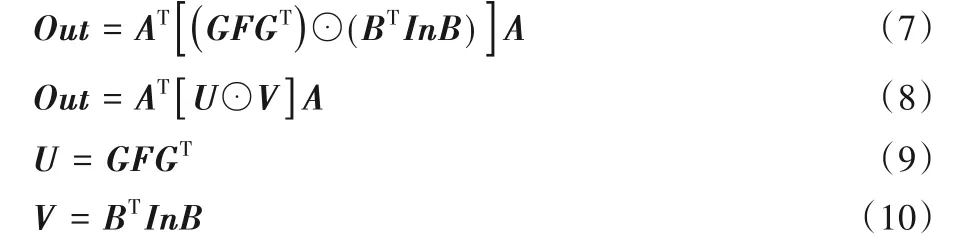
具体运算步骤如下：

记U⊙V结果为out：

随着压缩模型理论的提出和应用，现阶段的研究大多使用16位定点数据代替浮点数据，以减小计算资源和存储资源的开销。文献［10］研究结果表明，由于转换矩阵中的常数值范围会随参数n的增大而增大，使用16位定点数据时，卷积核的精度不能低于2-10，Winograd算法中参数n（n=m+r-1）不得大于8，否则将影响卷积神经网络的预测准确率。本文中分别使用多项式插值点（0，1，-1）、（0，1，-1，2，-2）及（0，1，-1，2，-2，1/2，-1/2）计算F（n=3，n=4）、F（n=5，n=6）及F（n=7，n=8）的转换矩阵AT、BT和G。常数乘法如上所述，通过移位操作或由2n或2-n的组合后再移位实现，使这部分运算不占用DSP资源。

相较于传统卷积算法，二维Winograd卷积算法的输出结果不再是输出特征图上的单个点，而是多个点组成的输出特征图子块。对一个大小为m2的输出特征图子块，二维Winograd卷积算法需要n2次乘法，而传统算法需要m2r2次乘法。

2 计算复杂度及带宽需求的定量分析

2.1 计算复杂度定量分析

由于二维Winograd卷积算法与传统卷积算法计算原理有差异，这一部分对二维Winograd卷积算法下应用5×5卷积和级联3×3卷积的计算复杂度进行了定量分析。

在此项工作的定量分析中默认步长为1，当通过卷积后输出特征图大小为C×C时，二维Winograd卷积算法乘法运算量为：(■C/■m×n)2。

由于m，n，r均为已知常数，设定C满足C/m为正整数，不考虑填充问题，可定量分析n≤8时二维Winograd算法下级联与非级联方法的计算复杂度。本文采用参数相同的常用F(m2，r2)实现级联。

使用两个F(22，32)级联时乘法运算次数为：

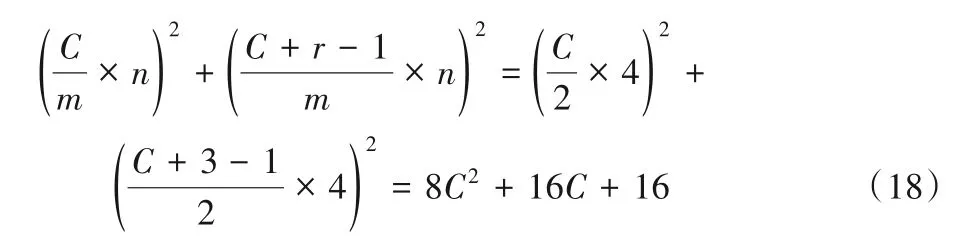
使用两个F(42，32)级联时乘法运算次数为：

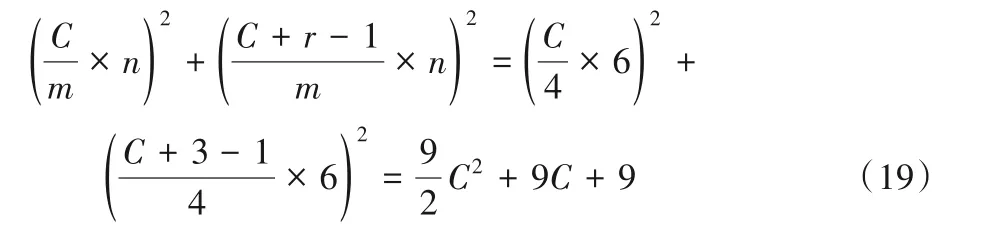
使用两个F(62，32)级联时乘法运算次数为：

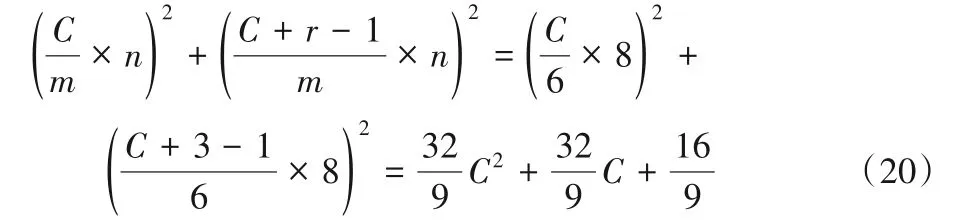
F(22，52)的乘法运算次数为：

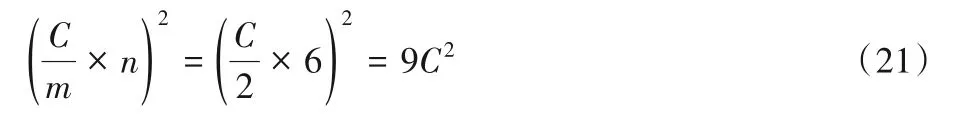
F(42，52)的乘法运算次数为：

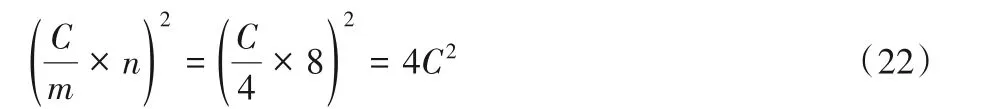
其中应用级联F(22，32)替代F(22，52)的过程如图1所示。

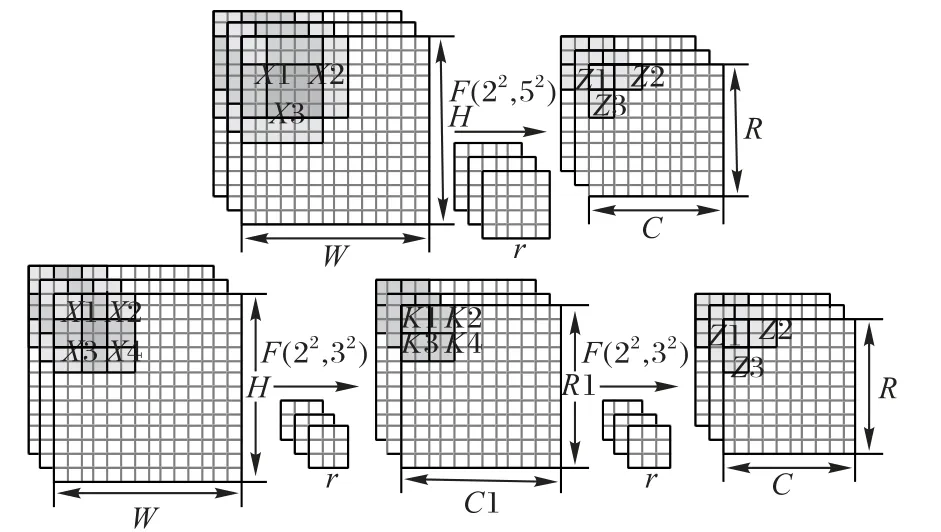
图1 级联F（22，32）替代F（22，52）示意图Fig.1 Schematic diagram of cascading F（22，32）to replace F（22，52）

通过对式（18）～（22）进行对比可以得出：F(42，52)的乘法运算次数是两个级联F(22，32)的约49.0%，两个级联F(42，32)的约87.1%，两个级联F(62，32)的约111.3%。此外，是传统卷积算法的约17%。

2.2 存储器带宽需求分析

为高效地利用硬件资源，数据传输速度必须大于或等于计算速度。存储器带宽需求越低，数据传输速度越快，为系统的准确性和稳定性提供保障。文献［11］采用基于列的双缓冲区数据布局完成设计，并未进行设计空间探索。文献［10］采用基于行的双缓冲区数据布局完成设计，使用参数组｛n，Pm，Pn｝指导设计空间探索。其中，n表示F(m2，r2)的尺寸，Pm表示并行运算的输入图像的通道数，Pn表示并行运算的卷积核的数目。本文设定参数对｛Pc，Px｝指导设计空间探索，其中与文献［10］相较，n=8，Pc=2Pm，Px=Pn。

对存储器带宽需求进行建模和定量分析。计算输入的n列数据所需时间为：

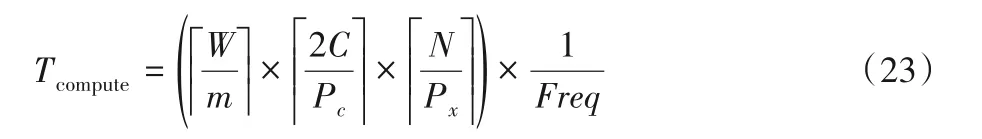
其中：C为输入图像通道数，N为卷积核中滤波器数目，Freq为工作频率。

m列数据并行传输所需的时间为：

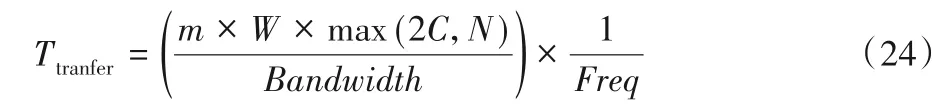
其中Bandwidth为存储器带宽。

由于要满足Ttransfer≤Tcompute，即传输时间小于等于计算时间。因此可得存储器带宽需求为：

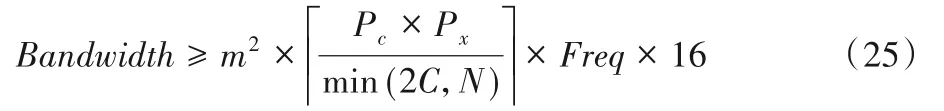
当不采用双缓冲区设计机制时，n列数据并行传输所需的时间为：

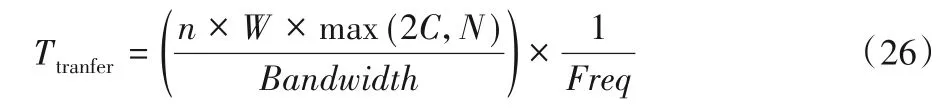
此时的存储器带宽需求为：

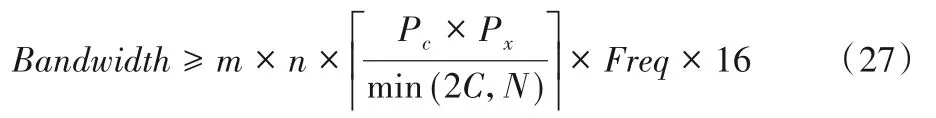
通过对比式（25）和式（27）可得，在理想状况下，双缓冲区设计方法可以缩减（1-m/n）倍的存储器带宽需求。这意味参数m相同时，卷积核尺寸越大存储器带宽需求越低。以F(42，52)、F(42，32)和F(62，32)为 例，三 者 分 别 能 够 缩 减50.0%（1-4/8）、33.3%（1-4/6）和25.0%（1-6/8）的存储器带宽需求。因此F(42，32)和F(62，32)的存储器带宽需求约为F(42，52)的1.32倍和1.50倍。本文的设计方法较基于F(42，32)的方法降低了约24.2%的存储器带宽需求。而F(62，32)的存储器带宽需求最高，无法完成高性能的卷积神经网络加速器设计。此外存储器带宽需求越高，数据重用能力就越差，存储器访问也越高，会大幅增加整个硬件加速器系统的能耗。

结合计算复杂度分析进行综合评定，基于F(42，52)的二维Winograd算法5×5卷积存储器带宽需求最低，计算复杂度也低于传统卷积算法和基于F(22，32)和F(42，32)的设计，且不存在级联卷积层间的计算延迟。

3 最小块单元双缓冲区数据布局方案

由于卷积神经网络规模庞大，计算过程复杂，且需要保证块随机存储器（Block Random Access Memory，BRAM）使用率和存储器带宽使用率均低于或趋近于DSP使用率，使得基于参数组｛n，Pm，Pn｝的设计空间探索求性能最优解的过程较为漫长。本文的设计将n确定为8，Pc=2Pm，极大地减少了可能的参数组合方式，大幅提高了设计空间探索速度。由于采用了存储器带宽需求最低的设计方法，因而仅需在探索过程中求解以BRAM资源为约束条件的性能最优解。

为快速高效完成设计空间探索工作，本文提出了一种双缓冲区最小块单元数据布局设计方案，计算和传输采用双缓冲设计并行完成。最初将输入特征图和卷积核等输入数据存储在外部存储器中，运算过程中的输入特征图和输出特征图通过FIFO传至FPGA平台。由于片上存储资源的限制，外部存储器中存储的数据将根据运算阶段分批次加载到片上存储器中。之后建立性能评估模型指导设计空间探索求解，对多种参数组合方式进行实验和数据对比，最终提出本文的设计方案。双缓冲区最小块单元设计如图2所示。首先存储三个紧邻的8×4×2（8行、4列、通道数为2）的图像块，如图2中A、B、C所示。其中选择通道维度的深度为2，既降低了设计空间探索复杂度，也不会对最终性能水平产生影响。每次取相邻的两个图像块参与二维Winograd算法5×5卷积运算，如AB和BC，每个最小块单元单个运算周期内执行128次乘法运算。当对AB进行运算后，A中的数据被覆盖，而后重用B中存储的数据，对BC进行运算。当完成最初前8行的运算后将自动翻转至下部分计算的最左端，以此类推向后循环，直至全部运算结束。

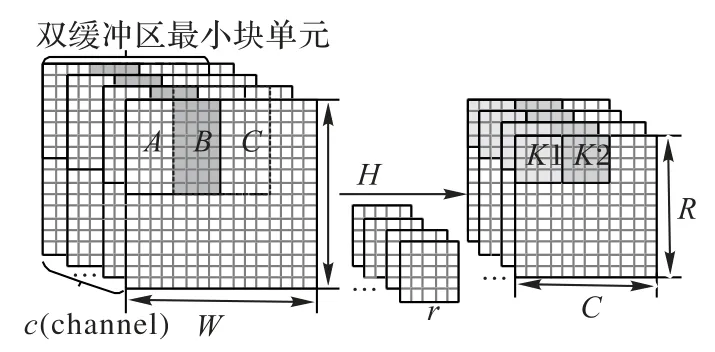
图2 双缓冲区最小块单元设计示意图Fig.2 Schematic diagram ofdouble-buffer minimum block unit design

通过性能评估模型数据评估得出的双缓冲区最小块单元设计，极大地降低了设计空间探索周期，也增强了可移植性。

4 6级流水线设计实现

如式（7）中所示，二维Winograd卷积算法F(42，52)计算需要逐步完成，首先完成U和V的加法计算，而后进行U⊙V的矩阵点乘运算，最后通过加法计算Out输出结果。根据二维Winograd卷积算法计算过程的这一特性，使用多级流水线设计可以有效降低各计算阶段间的延迟。

之前的二维Winograd卷积算法卷积采用4级流水线结构实现［10］。第1阶段并行执行U、V的运算，第2阶段执行U⊙V的运算，第3阶段执行Out的运算，第4阶段将各通道计算结果进行累加。这种设计方法在1级流水中完成U、V或Out的计算。在第1阶段V的运算过程中，V=BTInB的运算需要等待BTIn全部运算完毕后才能继续执行下一步与B的运算，使得加法计算过程的延迟可能会大于乘法计算的延迟，导致加速器性能下降。

另一种方法是将In中的元素设为未知参数，离线执行V=BTInB的运算，运算结果中V的元素全部转换为与In中元素相关的链式加法（如F(22，32)中V的首个元素为（x0-x2-x8+x10）），通过这种方式在1级流水中实现V的计算。但由于矩阵乘法的代数性质，该方法需要完成更多次的加法运算。以F(42，52)为例，此方法的加法运算量是逐步运算的近3倍，且部分常数乘法无法再由2n或2-n的组合进行近似。这些加法运算在FPGA中体现为大量触发器（Flip Flop，FF）和查找表（Look-Up-Table，LUT）的使用。

因此本文启用深流水线设计，采用逐步运算的6级流水线结构，合理分配硬件资源并减小处理转换矩阵中常数乘法所带来的误差。6级流水线设计结构如图3所示。对于V，在流水线的第1阶段，执行V1=BTIn的运算和存储，计算过程参考式（13），流水线的第2阶段，执行V=V1B的运算和存储，计算过程参考式（14）。对于U，有两种实现方式：第一种与V相同，流水线的第1阶段，执行U1=GF的运算和存储，计算过程参考式（11），流水线的第2阶段，执行U=U1GT的运算和存储，计算过程参考式（12）。由于U的运算量始终小于V，这种设计方法不会对流水线的延迟产生影响。第二种是直接离线完成U的运算并加载到FPGA的存储器中。由于卷积神经网络预测过程中卷积核权重不发生变化，U可以直接在FPGA外部完成计算。当参数n≤8时，V计算过程中的常数始终可以通过2n或2-n的组合进行精确表示，而U计算过程中会出现诸如1/6等需要进行近似处理的常数，因此这种方法可以在更高的卷积核精度下进行工作。相应地，离线完成U的运算代价是耗费更多的BRAM资源。为保障系统性能，本文选用第一种方法以节省片上BRAM资源。在流水线的第3阶段，执行U⊙V的运算并进行存储。流水线的第4阶段，执行Out1=ATout的运算并进行存储。流水线的第5阶段，执行Out=Out1A的运算并进行存储。流水线的第6阶段，将各通道的运算结果进行累加和存储。

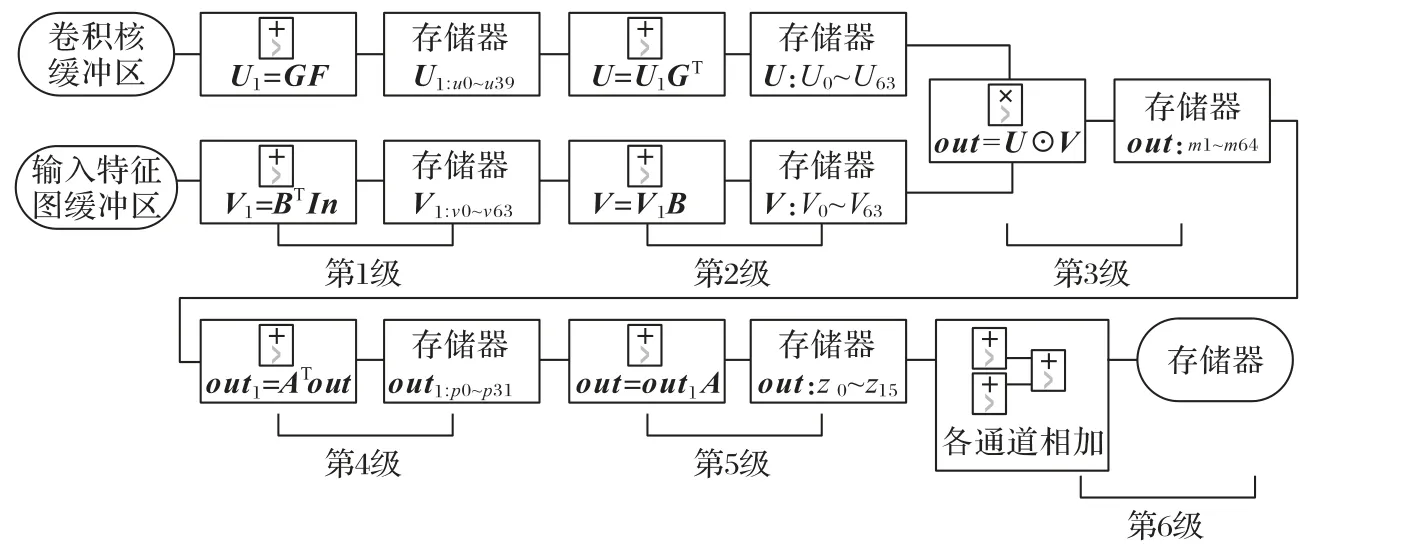
图3 六级流水线设计结构示意图Fig.3 Schematic diagram of 6-stage pipeline design structure

5 实验与结果分析

为验证针对5×5卷积所提出的双缓冲区二维Winograd算法6级流水线方法的综合性能，与现有文献［7，9-10］的针对5×5卷积的加速器设计方法就硬件资源使用率（设计方法所用的各类硬件资源占片上总资源量的比率）、计算性能和DSP效率等方面进行对比。实验选用AlexNet的第二个卷积层完成算法设计。为便于比较，采用高速集成电路硬件描述语言（Verilog integrated circuit Hardware Description Language，Verilog HDL）在Xilinx XC7A200T平台上完成双缓冲结构设计、加法器和乘法器的流水线设计等。利用Vivado simulator仿真工具建立寄存器转换级（Register Transfer Level，RTL）仿真模型，时钟频率与之前的多项研究工作保持一致，设为200 MHz。卷积神经网络模型预测过程的剩余部分在FPGA外部完成，确保所设计的算法不影响模型的预测准确率。

5.1 精度损失分析

采用ILSVRC2012数据集对本文所架构的AlexNet进行精度损失分析。训练数据集中有1 000个不同的类，每个类包含大约1 300个不同的图像，验证数据集中有5 000个与训练数据集不同的样本。本文采用16 bit定点数据完成量化，采用二维Winograd算法构建AlexNet，并与使用32 bit浮点数的全精度初始模型进行算法精度对比。

如表2所示，本文AlexNet模型的Top-1精度损失不超过0.5%，Top-5精度损失不超过1%，与文献［7］方法、文献［9］方法和文献［10］方法大致相同。其中文献［9］方法和文献［10］方法精度损失均<1%，文献［7］方法由于使用8 bit数据量化因而精度损失略高，约为<3%。

表2 精度损失分析 单位：%Tab.2 Accuracy lossanalysis unit：%

5.2 计算性能分析

乘法运算量是影响卷积神经网络FPGA加速器实际计算时间的主要因素。本文统计传统卷积方法、文献［7］方法、文献［9］方法、文献［10］方法和本文方法的AlexNet第二卷积层乘法运算量，并与传统卷积方法进行加速倍率比较。

由表3可以看出，本文算法5×5卷积的乘法运算量最低，加速倍率最高，为5.82，是其他方法的1.13～2.91倍。

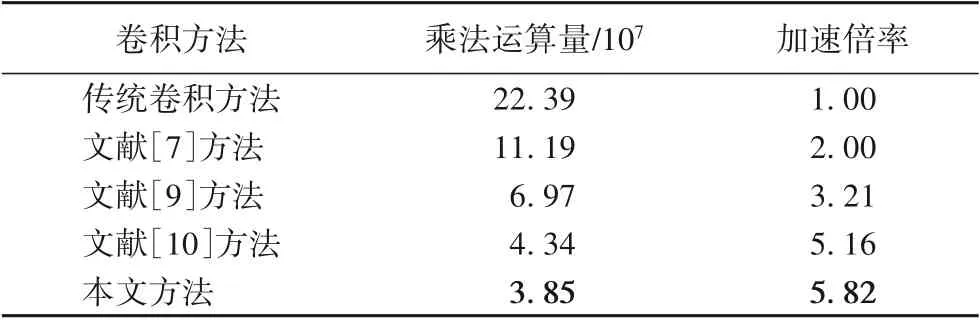
表3 乘法运算量对比Tab.3 Comparison of multiplication computational cost

在各类卷积神经网络FPGA加速器中，实际运算时间直观地反映了架构方案的加速水平，是评估加速器性能的重要指标。本文对比并分析了文献［7］方法、文献［9］方法、文献［10］方法和本文方法的AlexNet第二卷积层运算时间，并以文献［7］方法的计算速度为基线比较了各类方法的加速效果。

由表4可知，得益于最低的乘法运算量、深流水线架构和不存在级联卷积的层间计算延迟等优势，本文的方法运算时间最短，对5×5卷积的加速效果最佳。

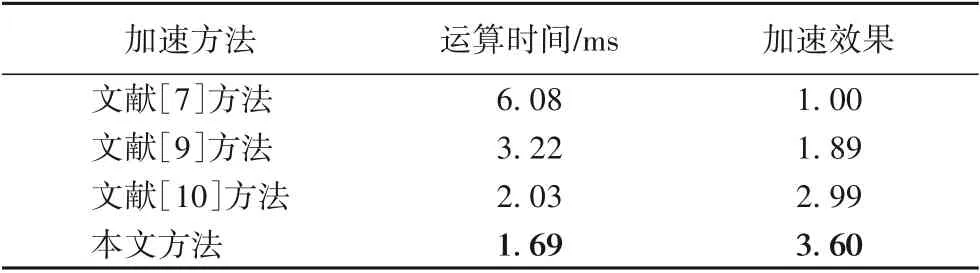
表4 运算时间对比Tab.4 Comparison of computing time

5.3 硬件资源使用率分析

根据文献［7，9-10］的设计思想，使用本文的FPGA平台实现其相应算法对AlexNet第二个卷积层的设计，就DSP、LUT和BRAM的资源使用率进行比较。硬件资源使用率对比如图4所示。

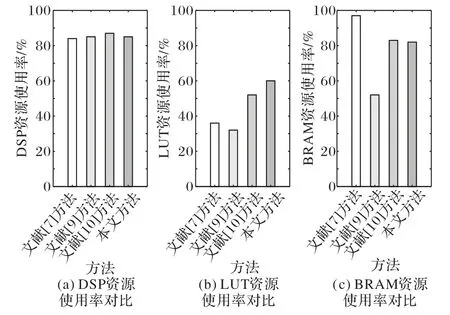
图4 硬件资源使用率对比Fig.4 Hardware resource utilization comparison

如图4（a）所示，本文的DSP资源使用率与文献［7］方法、文献［9］方法和文献［10］方法相近，均在80%以上，均能保证卷积神经网络硬件加速器拥有较高的工作效率。

如图4（b）所示，本文的LUT资源使用率比文献［7］方法高24%，比文献［9］方法高28%，比文献［10］方法高8%，但远低于DSP资源使用率。由于二维Winograd卷积算法通过完成大量加法运算来降低乘法运算量，因此采用Winograd算法的本文和文献［10］需要更多的LUT资源完成加法运算。

此外在Winograd算法U、V及Out的加法计算过程中，存在一些可复用的中间计算结果，例如F(22，32)算法运算过程中式（12）运算结果U的第2、3个元素中均有（u0/2+u2/2）的运算，其中u0、u2为式（11）运算结果U1的第1、3个元素。为降低部分LUT开销，本文通过字符串精确匹配搜索U、V及Out加法运算中可复用的中间计算结果来指导设计，在二维Winograd卷积算法的加法设计中探索并实现最优的数据重用方式，降低了约8%的加法计算量，以降低LUT资源使用率。这种加法运算中间结果重用方法避免了部分无效计算，减小了设计面积且降低了系统能耗。

如图4（c）所示，本文的BRAM资源使用率比文献［7］方法低15%，比文献［9］方法高30%，比文献［10］方法低1%。与文献［7］和文献［9］的方法相较，本文和文献［10］的方法相对乘法运算量更低，这意味着在使用相同数目的DSP时，二维W inograd卷积算法可对更多的输入数据完成卷积运算，因此采用此类方法的本文和文献［10］在实现过程中需要占用更多的BRAM资源。本文通过设计快速设计空间探索性能分析模型来保证BRAM资源使用率低于DSP使用率，以确保加速器性能不受硬件资源数量限制。

综合整体硬件资源进行分析，本文的设计与之前研究工作相较各项硬件资源使用率相近，通过数据重用、优化架构和优化加速算法等方式取得了更高的计算性能，提高了硬件加速器的加速效率。

5.4 DSP效率分析

由于卷积神经网络FPGA加速器的吞吐量、功率和能量效率等性能指标均会受FPGA平台影响，同一设计方法在不同平台上会有不同的性能表现。因此本文将DSP效率，即吞吐量/片上DSP数量作为主要指标以客观分析加速器性能水平。由于本文在同一FPGA平台上实现相关设计因此各加速方法具有相同的工作频率和可用DSP总量。

由表5可知，本文的设计在5×5卷积的相关层达到了较高的DSP效率，DSP效率为0.529，高于文献［7］方法和文献［9］方法，由于复用了部分加法运算结果降低了吞吐量而略低于文献［10］方法的0.557。但因本文架构方法有着更低的乘法运算量和存储器带宽需求，因此相较文献［10］方法，本文的加速器系统架构方法速度更快、能耗更低、性能更优。

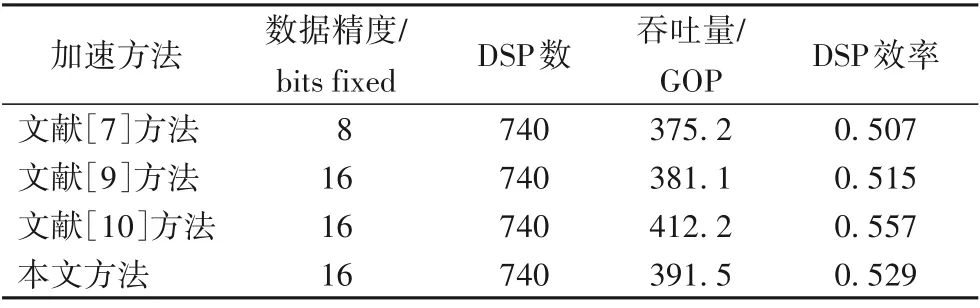
表5 DSP效率对比Tab.5 Comparison of DSPefficiency

6 结语

本文对基于二维Winograd算法5×5卷积的架构问题进行了研究，深化二维Winograd卷积算法流水线并利用双缓冲区和复用中间运算结果实现数据重用，提出了一种针对二维Winograd算法5×5卷积的双缓冲区最小块单元6级流水线方法，并与现有构建5×5卷积的方法进行实验对比。实验结果表明，本文提出的深流水线方法在基本不影响神经网络预测准确率的前提下，具有更低的计算复杂度和存储器带宽需求，缩短了计算时间，降低了能耗，为FPGA上5×5快速卷积的架构提供了解决方案，有效地提高了二维W inograd算法5×5卷积在FPGA平台上的计算效率。