基于改进帝国竞争算法的柔性作业车间机器故障重调度

张国辉，陆熙熙，胡一凡，孙靖贺

（郑州航空工业管理学院管理工程学院，郑州 450015）

0 引言

作业车间调度问题一直是制造业中的重点关注对象，车间调度的主要目的是节省产品的生产时间，让生产资源的利用率发挥最大作用，最后通过对资源的恰当分配让柔性作业车间的生产效率更高。柔性作业车间调度问题（Flexible Jobshop Scheduling Problem，FJSP）是经典车间调度的延伸，扩展了每道工序的机器柔性，相对经典车间调度来说较为繁杂。在实际的生产制造过程中，车间环境是动态变化的，会出现各种各样的问题，比如紧急插单、机器故障等不确定性因素，要充分考虑到当前工作环境及系统的状态，及时作出正确合理的调度方案，因此就出现了柔性作业车间动态重调度问题。在1977年，Nelson等［1］对于动态调度问题，提出了将动态问题转化为多个连续的静态区间，对每个区间进行优化，以达到总体最优。柴永生等［2］根据动态调度问题提出了免疫遗传算法，即对进化种群进行免疫操作，有效地解决了搜索效率低的问题。孟冠军等［3］在求解多目标柔性作业车间调度问题上设计了改进混合人工蜂群算法，即在不同的阶段采用不同的搜索机制，并且为了提高得到最优解的概率，将禁忌搜索与改进的混合人工蜂群算法结合。Shahrabi等［4］针对考虑随机作业到达和机器故障的动态作业车间调度问题，提出了一种基于变量邻域搜索的调度方法，结合事件驱动策略，为了在任意重调度点获得合适的参数，采用了基于Q因子算法的强化学习算法，并通过模拟作业车间实验结果表明该方法的性能明显优于常用调度规则和一般可变邻域搜索。He等［5］在研究机器故障状态下的动态调度问题时，为了提高调度的鲁棒性和稳定性，首先提出了一种新的空闲时间插入策略，其次提出了加工路线变更策略和右移策略相结合的策略，在这两种策略的基础上，提出了一种多策略调度算法。邹攀等［6］提出一种基于分层蚁群遗传算法的车间资源驱动的多目标调度方法，适用于车间资源变化、任务执行情况变化、紧急任务插入等不确定情况下的动态调度。吴正佳等［7］在研究机器发生故障的柔性作业车间动态调度问题时，提出了两种重调度策略即插入重调度和完全重调度，并结合改进遗传算法（Genetic Algorithm，GA）进行求解，将机器故障产生的影响降到最低。孙丽珍等［8］采用改进遗传算法结合启发式规则求解柔性作业车间问题；针对工件加入和机器故障的动态调度，提出了加入多约束的贪婪插入空隙法的解码方式的改进遗传算法。Nouiri等［9］以最小最大完工时间和鲁棒性为目标，在求解机器故障下柔性作业车间调度问题上，提出了一种两阶段粒子群优化算法，实验部分与Al-hinai等［10］提出的混合遗传算法进行比较，结果表明该优化算法具有更好的鲁棒性和稳定性。近年来，随着可持续发展战略的提出，越来越多的生产企业开始转向绿色制造，降低能源消耗已经成了焦点问题。Nouiri等［11］在解决机器故障下的动态柔性作业车间调度问题时，以最大完工时间最小、全局能耗最小为目标，提出了一种基于粒子群优化方法的绿色重调度方法，可以最大限度地减少时间和降低能耗。包哲人等［12］面向考虑能耗的柔性作业车间调度问题提出了改进离散蝙蝠算法，为避免算法早熟收敛设计了一种具有记忆能力的粒子变异操作，同时为了算法的搜索能力加入惯性权重策略，通过生产实例验证了算法的有效性。陈超等［13］以平均流经时间和能耗为目标建立柔性作业车间模型，针对此模型提出了遗传算法与模拟退火混合算法（Genetic and Simulated Annealing Algorithm，GASA），采用滚动窗口技术结合GASA来求解机器故障的动态调度问题并验证了算法的有效性。曹庆奎等［14］针对在机器故障情况下，同时考虑能耗和交货期的柔性作业车间动态调度问题，采用GASA进行求解，以最大完工时间最小、能耗最小、客户满意度最大为目标验证了其算法的有效性。李明等［15］针对考虑准备时间的低碳FJSP，提出了新型帝国竞争算法（Imperialist Competitive Algorithm，ICA），采用一种全新的同化方法和归一化总成本新定义，在优化关键目标的同时持续改进非关键目标总能耗。吕聪等［16］提出协作混合帝国算法，改进了自适应参数，提高了算法的收敛速度，并对不同阶段采用多变异改革策略以提高算法的局部搜索效率，以及协作交流机制来提高算法的全局搜索能力，表明了协作混合帝国算法在求解柔性车间调度问题上的稳定性和优越性。以上针对动态调度问题的研究，在国内外学者的努力下研究成果丰富，但是针对机器故障重调度，并同时考虑能耗的研究相对较少。机器故障在实际车间生产过程中是很常见的动态事件，在发生故障后找到合适的重调度方案是非常重要的。本文主要研究机器故障的柔性作业车间重调度问题，对帝国竞争算法进行改进，在同化和革命操作之后加入一个轮盘赌的选择机制，对同化和革命后的个体重新进行选择，并结合事件驱动策略对此类重调度问题进行求解，验证算法的有效性。

1 问题描述

柔性作业车间调度问题可以描述为：将1到n个工件合理安排到m台机器上进行加工，每个工件有多道工序，其中每道工序都可以选择不同的机器进行加工，各工序所选机器不同，所需加工时长也不相同。在实际生产过程中存在一些不确定性因素，导致会出现各种动态事件，本文考虑的是机器故障的动态事件。柔性作业车间动态重调度研究存在以下几个假设条件：

1）同一个工件在同一时刻只能由一台机器进行加工，一台机器在同一时刻只允许有一个工件在该机器上加工。

2）每一道工序可以选择由可加工机器集中的机器进行加工，但是同一时刻只允许在一台机器上加工。

3）每一个工件对于每道工序的加工有先后顺序要求，只有某工件的前道工序加工完成后才能对该道工序进行加工。

4）当原调度已经对工件的前几道工序加工完成，再调度时只需加工该工件的后续工序。

柔性作业车间机器故障重调度问题是在给出相关变量和决策变量，满足约束条件和目标函数的情况下，生成一个初始调度，在机器发生故障后，初始调度方案便不可行，此时应重新调整调度方案，结合重调度策略生成重调度方案。

1.1 变量定义

本文的相关变量符号及定义如表1所示。

表1 变量描述Tab.1 Variables description

本文的决策变量有∂ijk和δijhdk，其中，∂ijk用于确定工序与机床的选择关系；δijhdk用于确定工序在机器上的优先加工顺序。

1.2 约束条件

柔性作业车间调度问题要满足工件约束和机器约束：

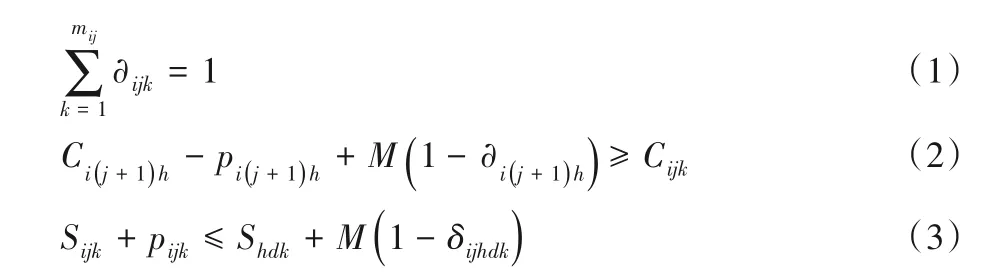
式（1）表示一道工序只能在一台机器上加工；式（2）表示同一工件只能在前一道工序加工完才能加工后一道工序；式（3）表示一台机器在同一时刻只能加工一道工序。

1.3 目标函数

本文主要研究的调度目标为最小化最大完工时间（makespan）、最小能耗以及最小总延迟时间，如下所示：1）最小化最大完工时间。

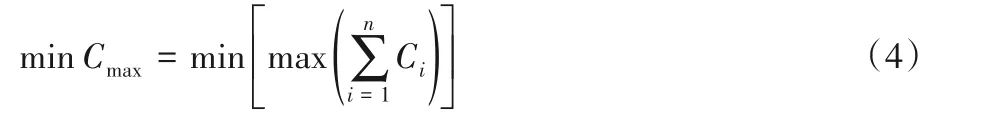
2）最小能耗。

采用文献［13］中的加工能耗E的表示方法，每台机器上的第一个工件的开始加工时刻就是该台机器的开工时刻，机器一直保持着耗能状态，直到该机器上所有工件都加工完毕，因此能耗的数学模型为式（5）所示：

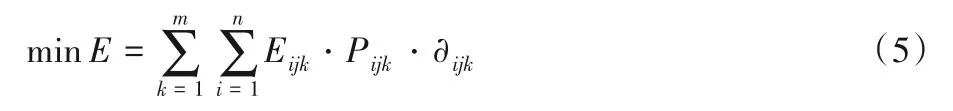
3）最小总延迟时间。

本文总延迟时间主要是计算机器故障前后，两次调度的最小化最大完工时间差，总延迟时间的数学模型如式（6）所示：

由于三个目标的量纲不统一，需要进行归一化处理，将各目标数据转换到［0，1］内，计算过程如式（7）所示：

其中：x*表示归一化之后的目标值，x为当前目标值，xmax为全局目标最大值，xmin为全局目标最小值。

对本文的三个目标进行归一化处理后，再采用线性加权和法，将三个目标优化问题转变成单目标优化问题，如式（8）所示：

2 FJSP动态重调度策略

动态重调度策略，是指在系统生产过程突发情况下将采取应对措施来解决发生的异常事件。一般用到的策略方法有三种，分为事件驱动、周期驱动和周期与事件的混合驱动，本文采用事件驱动策略。

当机器出现故障时，确定机器修复时间T，故障点前已经加工过的工序保持不动，找出故障点后未加工的工序，并对其用帝国竞争算法进行重新调度，故障机器的开工时间为修复后的时间，即故障时刻加上故障时长，其余机器的开工时间为当前正在加工工序的完成时间。机器发生故障后，在该机器上未进行加工的工件将被分配到其他机器上进行加工。机器故障重调度的具体流程如图1所示。

图1 机器故障重调度流程Fig.1 Flow of reschedulingwith machinebreakdown

3 算法设计

3.1 基本帝国竞争算法

帝国竞争算法是一种受帝国竞争行为启发的新的智能优化算法，它与粒子群优化（Particle Swarm Optimization，PSO）算法、蚁群优化（Ant Colony Optimization，ACO）算法等一样，都属于基于群体的随机优化搜索算法。帝国竞争算法比PSO和GA收敛速度快，具有较强的全局收敛性，并且同化和革命步骤又保证了算法的局部搜索能力，因此在求解柔性作业车间调度问题上有一定的优势。帝国竞争算法在解决各种实际的优化问题上具有广泛应用，本文将其应用在解决机器故障重调度问题上。

ICA的基本过程为：产生初始帝国、同化、革命、帝国竞争和帝国消亡。ICA的流程如图2所示，具体步骤为：

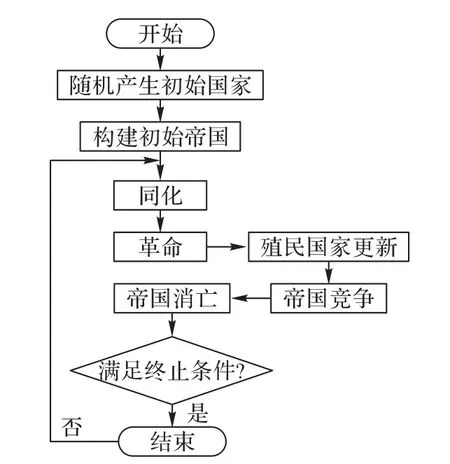
图2 ICA流程Fig.2 Flowchart of ICA

步骤1 将随机产生的Npop个初始解作为初始国家，并计算每个国家的成本cn。

步骤2 构建初始帝国。选择成本较小的Nimp个国家作为殖民国家imp，剩余的作为殖民地Col，殖民地的个数NCol与殖民国家个数Nimp之和等于初始解的个数Npop。确定殖民国家所能分到的殖民地数量，随机分配殖民地给各殖民国家，此时各殖民国家与其殖民地组成初始帝国PEmp。殖民国家所拥有的殖民地数量与其势力成正比，因此要先计算每个殖民国家的标准化成本Cn，如式（9）所示：

殖民国家的成本越小，势力就越大，每个殖民国家的标准化势力pn如式（10）所示：

第n个殖民国家所拥有的初始殖民地数量NCn如式（11）所示：

其中round是将小数四舍五入成整数的函数。

步骤3 同化和革命。将殖民地向其所在殖民国家移动，即殖民地都趋向于殖民国家这个最优解；革命的目的是防止同化后的算法过早收敛。同化操作分为机器的选择和工序排序两部分，机器的选择部分采用多点交叉变异的方法，具体操作为：随机选取r个位置，将殖民国家的r个位置的信息替换到殖民地中的对应位置，其余位置信息保持不变；工序排序部分采用工件交换的方式，将殖民地的加工工序部分与殖民国家的加工工序部分进行信息交换，更新殖民地的加工工序部分。革命操作同样分为机器的选择部分和工序排序部分，在机器选择部分，随机选取某个加工机器，然后选择对应机器集中的其他任一机器代替它；在工序排序部分，随机选择两个位置上的工序进行信息交换。同化和革命后的新帝国为SEmp。

步骤4 殖民国家更新。当殖民地经过同化和革命后，将殖民国家和所有殖民地的成本进行比较：若有殖民地的成本比殖民国家要小，则该殖民地替代殖民国家成为该帝国内新的殖民国家；否则，殖民国家不发生变化，更新后的帝国为Emp。

步骤5 帝国竞争。计算所有帝国的总成本，较弱帝国需选出一个最弱殖民地，较强帝国可以来争夺殖民地，帝国越强获得该殖民地的概率越大。每个帝国的总成本TCn计算如式（12）所示，将每个帝国的总成本进行标准化处理，如式（13）所示，每个帝国占有弱殖民地的概率Pn计算如式（14）所示：

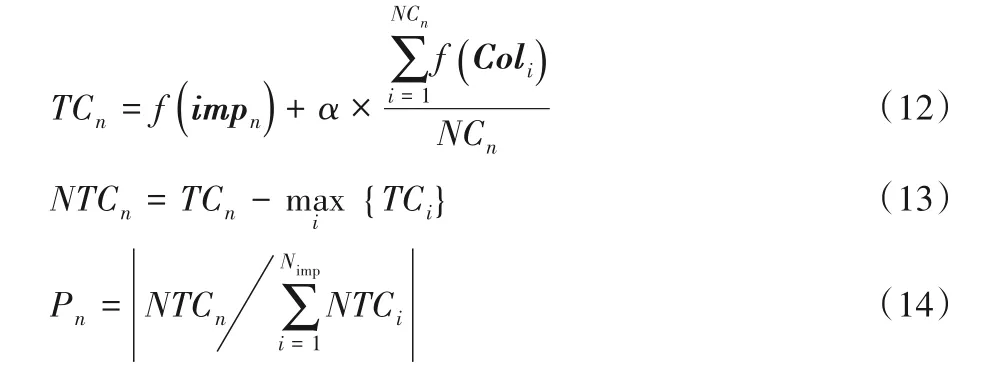
其中：f（impn）表示第n个帝国的殖民国家的成本，f（Coli）表示第i个殖民地的成本，α为殖民地影响因子，0<α<1，NTCn表示第n个帝国的标准化成本。

步骤6 帝国消亡。当某个帝国没有任何殖民地时，此时该帝国消亡。

步骤7 若终止条件成立，则算法结束；否则回到步骤3。

3.2 编码和解码

在ICA中，每一个国家代表一组柔性作业车间动态调度问题的可行方案，结合柔性作业车间调度问题特点设计两段式实数编码方式对国家个体进行编辑。

以图3为例，每个个体为一串整数，总长度为2L，L为所有工序的个数，Oi表示工件i的工序数。左半部分为加工机器的选择，按照工件1、工件2和工件3的工序顺序进行排列，每个整数表示对应工序可选加工机器的排列序号，第一个整数3为工序O11可选机器集｛M2，M3，M4｝的第3个机器即M4。右半部分为加工工序的排序，每个整数代表工件号，第1次出现表示该工件的第1道工序，第2次出现表示该工件的第2道工序，以此类推，图3中加工工序所表示的工序顺序为（O21，O11，O31，O12，O32，O22）。

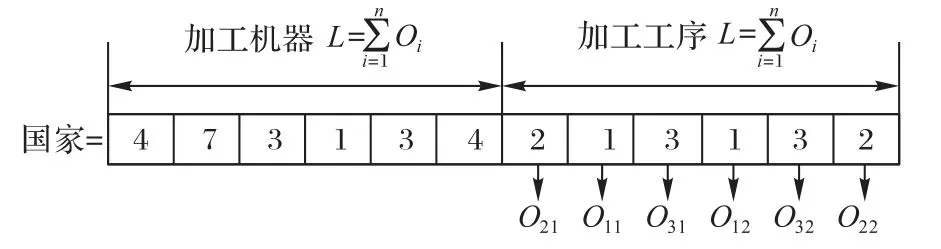
图3 编码表达示意图Fig.3 Schematic diagram of codingexpression

对国家个体进行解码操作时，首先对个体的前半部分即机器部分从左到右依次进行解码，转成对应的机器并确定各工序在对应机器上的加工时间，然后对个体的后半部分即工序部分进行解码，解码成活动调度。

3.3 改进ICA

帝国竞争算法中的同化是通过殖民地向殖民国家的移动来实现，相当于是一个寻优过程增强了算法的局部搜索能力，但是在传统的帝国竞争算法中并没有物竞天择的进化规律，在ICA求解调度时为了能够提高求解质量、提高算法的寻优能力，因此本文参照遗传算法中的遗传和变异对帝国竞争算法进行改进，在初始帝国进行同化和革命之后增加一个选择机制的步骤，可以使初始帝国中的优秀基因得以保留，更新后的帝国质量更优，更加贴近最优解。选择机制的具体操作如下：

步骤1 首先将初始帝国PEmp中的第一个帝国PEmp（1）的所有个体与其同化和改革后的SEmp中对应的第一个帝国SEmp（1）中的所有个体放在一起。

步骤2 采用轮盘赌的方法从合并的帝国中选出一半数量的个体，将其作为一个新的帝国Emp（1）。本文采用轮盘赌的个体概率值为各个国家的成本值的倒数，成本值越小则被选到的概率越大，否则概率越小。

步骤3 从新帝国中选出成本值最低的国家作为殖民国家，剩余的国家则沦为该殖民国家的殖民地。

步骤4 接着转到步骤1进行初始帝国PEmp中的第二个帝国PEmp（2）和同化和改革后的SEmp中对应的第二个帝国SEmp（2）的合并，以此类推，直到所有帝国全部选择完成，最终生成新的帝国Emp，此时选择机制结束。

改进帝国竞争算法选择机制的示意图如图4所示。

图4 选择机制示意图Fig.4 Schematic diagram of selection mechanism

改进后的帝国竞争算法的流程如图5所示。

图5 改进ICA流程Fig.5 Flow of improved ICA

4 仿真结果与分析

采用改进ICA对柔性作业车间机器故障重调度算例进行仿真实验，并随机假设三种机器发生故障的场景，得出最佳调度方案，验证该算法求解柔性作业车间机器故障重调度问题的有效性。

4.1 参数设置

本文的实验算例来自洛阳某钢具厂生产车间，经过简化为8×8的柔性作业调度问题，如表2所示，有8个工件，8台机器。表3为每台机器的加工能耗，表4为假设的三种机器故障场景，这三种场景分别独立发生。

表2 仿真实例数据Tab.2 Dataof simulation examples

表3 机器能耗Tab.3 Machineenergy consumption

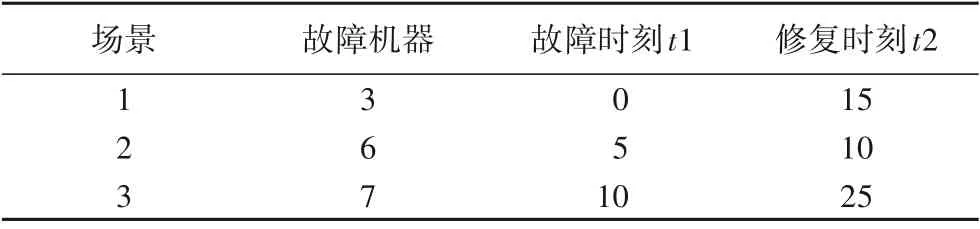
表4 三种机器故障场景Tab.4 Three scenarios of machinebreakdowns

使用Matlab 2017b对该算例进行仿真实验，本文提出的算法参数设定为：最大迭代次数为50，国家个数为100，帝国个数为10，a、b、c分别设为0.3、0.3、0.4。针对同化系数、革命概率和竞争概率三个参数，采用田口方法以及Minitab软件进行多因子正交实验，正交表如表5所示，每个参数有3个水平，共有9种不同的组合，对该正交表进行田口分析得到的均值主效应图如图6所示，最后得出同化系数、革命概率和竞争概率的参数分别为0.7、0.05、1。

表5 正交表Tab.5 Orthogonal table

图6 参数均值主效应图Fig.6 Main effect plots of parameter means

4.2 实验结果

首先在初始时刻采用改进ICA对问题进行调度，得到初始方案，如图7所示为迭代最优解的甘特图，最大完工时间为26 min，能耗为624.3 J。图7中相同颜色代表同一工件，其中颜色块上的数字表示为：第一个数字是工件号，后两位数字表示工序号，如“101”表示工件1的第一道工序，“402”表示工件4的第二道工序。

图7 初始调度方案甘特图Fig.7 Gantt chart of initial scheduling scheme

场景1是机器3在0时刻发生故障，故障修复时刻为15，进行重调度后的甘特图如图8所示，最大完工时间为27 min，总延迟时间为1 min，能耗为722.8 J。图8中数字表示工件号，相同颜色代表同一工件，机器3上，［0，15］时间段为故障区间。

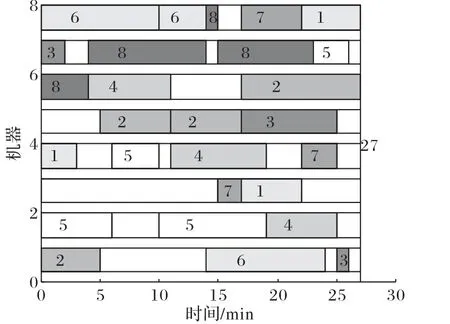
图8 机器3发生故障后的重调度甘特图Fig.8 Gantt chart of rescheduling after machine 3 breakdown

场景2是机器6在5时刻发生故障，故障修复时刻为10，进行重调度后的甘特图如图9所示，最大完工时间为27 min，总延迟时间为1 min，能耗为757.6 J。图9中标有数字的白色部分表示机器发生故障时刻之前的工序保持原调度不变，有颜色的部分表示机器发生故障后重新进行调度的工序。

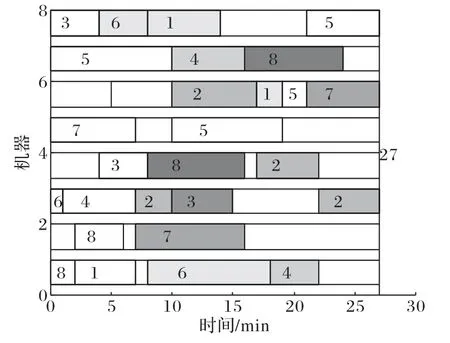
图9 机器6发生故障后的重调度甘特图Fig.9 Gantt chart of reschedulingafter machine6 breakdown

场景3是机器7在10时刻发生故障，故障修复时刻为25，重调度后的甘特图如图10所示，最大完工时间为27 min，总延迟时间为1 min，能耗为707.3 J。

为进一步验证改进ICA的有效性，假设机器2、机器5和机器6分别在0时刻发生故障，并且短时间内无法修复，针对该三种机器故障情况采用GASA［13］、改进GA［8］和改进ICA分别进行求解并对比，三种算法求出的三种优化目标数据如表6所示，从表中可以看出该改进ICA与其他两种算法相比实验结果更好，验证了该算法的有效性。

表6 实验数据对比Tab.6 Comparison of experimental data

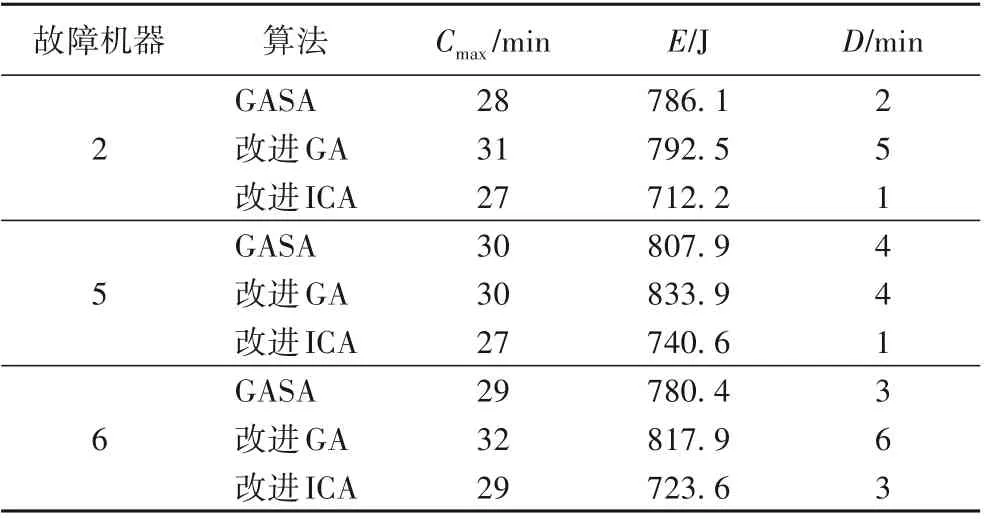
故障机器D/min 2 5 6算法GASA改进GA改进ICA GASA改进GA改进ICA GASA改进GA改进ICA C max/min 28 31 27 30 30 27 29 32 29 E/J 786.1 792.5 712.2 807.9 833.9 740.6 780.4 817.9 723.6 251441363

为了验证算法求解的稳定性，分别采用三种算法对上述机器2发生故障的情况进行求解，表7为三种算法运行10次的各优化目标的平均值和方差，从表7中可以看出，改进ICA与GASA、改进GA相比各优化目标的方差最小，表明该改进ICA求解的稳定性最好。

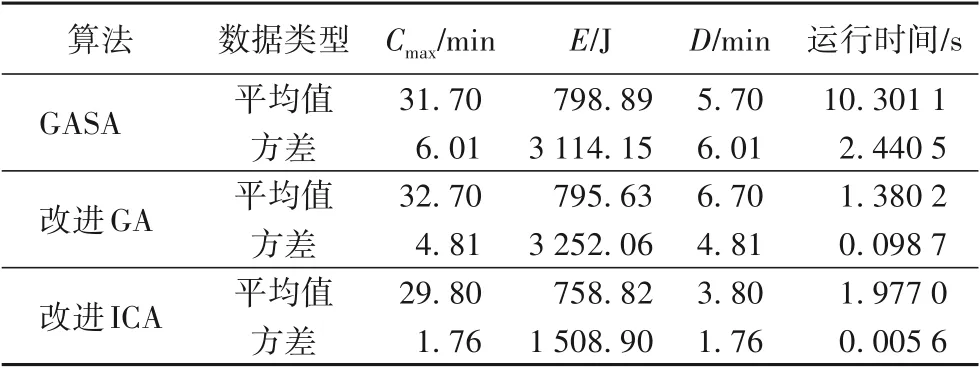
表7 三种算法的性能对比Tab.7 Performance comparison of threealgorithms

针对上述假设的机器故障情况的实验研究以及与遗传算法进行比较，可以得出的结论是，故障后的重调度方案的最大完工时间、总延迟时间以及能耗都控制在一个较好的范围之内，符合实际生产需要。

5 结语

本文针对柔性作业车间机器故障的动态事件，对帝国竞争算法进行改进，加入选择机制操作，结合事件驱动策略以及最大完工时间、能耗和总延迟时间三个目标函数，对该类动态问题进行求解。对提出的三种不同机器故障的场景进行实验仿真分析，得出的结果较为符合实际生产需要，并将改进ICA与两种不同的算法进行比较，验证了该算法的有效性和可行性。

柔性作业车间生产过程中容易受到各种复杂因素的影响，下一步将继续对帝国竞争算法进行改进，并运用到其他类型的动态调度中，如插入紧急订单、工件延误等动态事件。