核级铅酸蓄电池组的抗震性能分析

魏圣坤 赵 斌

（同济大学土木工程防灾国家重点实验室，上海200092）

0 引 言

核能发电具有对环境污染小、消耗资源较少等优点，已逐渐成为各国电力行业的主要发展对象。但核能发电在地震中的安全问题也不容忽视，2011年福岛核电站受地震影响，放射性物质泄漏到外部，造成的损失无法计量［1］。而蓄电池系统是核电站发生事故时的备用电源，在地震时要确保供电，其在地震作用下的完整性对核电站的意义不言而喻。但蓄电池的质量远大于支架的质量，并且蓄电池是单个的散体，与支架之间没有牢固的连接，所以对蓄电池系统进行抗震分析具有一定难度［2］，而在此之前对蓄电池系统的抗震性能研究较少，尚未给出较为适宜的简化建模方法，因此本文基于同济大学振动台实验室对核级蓄电池组及支架样品进行的抗震试验研究结果，并使用ABAQUS采用固体单元和壳体-弹簧单元模拟蓄电池两种建模方式进行谱分析法计算支架地震响应，对比试验结果后得出较为蓄电池的合理简化建模方法。

1 试验设计

1.1 试验模型

本次试验模型由核级铅酸蓄电池、支架柱、支架横梁、支架柱底板、蓄电池底部槽钢、底部方钢管、垫木、过渡钢板组成。蓄电池选用9个GFH-3000蓄电池，支架柱尺寸为1 776 mm×140 mm×570 mm，支架梁长为1 025 mm，支架柱底板尺寸为1 916 mm×250 mm，厚度为10 mm，蓄电池底部槽钢长为885 mm及735 mm，蓄电池底部方钢管尺寸为1 776 mm×90 mm×50 mm，厚度为5 mm。支架柱底部垫木尺寸为1 916 mm×250 mm×35 mm，支架结构采用胶垫厚度为2 mm～12 mm不等。锚地螺栓采用M20、M12、M10高强螺栓，支架间连接采用M10高强螺栓。试验模型如图1所示，蓄电池组及支架的结构三视图见图2。

图1 试验模型Fig.1 Model used in the experiment

图2 蓄电池组及支架结构三视图（单位：mm）Fig.2 Three views of battery pack and support structure（Unit：mm）

1.2 试验方案

根据“HAF J0053核设备抗震鉴定试验指南”［3］的要求，对设备进行动态特性探测试验、1/2SSE和SSE抗震鉴定试验、基准性能试验和功能检测等［4］。其中SSE为安全停堆地震，是指可能发生的最大地震。动态特性探测试验采用频率范围为0.2～100 Hz，加速度幅值为0.20g的白噪声随机波，分别在X、Y、Z三个正交轴向对蓄电池组进行振动激励，持续时间不少于120 s，以测定蓄电池组的自振频率和阻尼比。在1/2SSE和SSE抗震鉴定试验时［5］，在X、Y、Z三个方向输入人工地震波，持续时间为30 s，强震部分20 s，信号超过其最大值70%峰值的个数大于8个，抗震试验顺序为5次1/2SSE抗震鉴定试验和1次SSE抗震鉴定试验，抗震鉴定试验要求的反应谱见表1（阻尼比均为0.05）。在抗震试验前、后对蓄电池组进行基准性能试验，抗震试验过程中对蓄电池组进行功能监测，监测蓄电池组放电电力和总电压信号。所有试验工况中，电池组均处于通电工作状态。

表1 抗震鉴定试验要求的反应谱Table 1 Response spectrum required by seismic qualification test

2 ABAQUS建模

采用大型通用有限元软件ABAQUS对支架结构进行建模。建立两个有限元模型，模型1的蓄电池仅考虑了蓄电池的质量，采用实体单元建模；模型2的蓄电池考虑铅酸蓄电池内部酸液在地震作用下会产生液体动力效应，从而采用壳单元及弹簧单元进行简化建模，两模型总质量相等。

计算模型及坐标轴定义如图3所示，长度方向为Y向，宽度方向为X向，高度方向为Z向。

图3 ABAQUS有限元模型Fig.3 ABAQUS finite element model

2.1 建模方法

两个模型对于蓄电池支架柱、横梁、底板、蓄电池外壳、耐酸胶垫等均采用壳单元（shell）模拟，螺栓以及木材等模拟采用实体单元，约束长度模拟真实情况。模型2的蓄电池内酸液采用欧标EN1998-4—2006［6］中的弹簧简化方法简化为集中质量及弹簧单元，计算公式如式（1）-式（7）所示，简化模型示意图如图4所示。蓄电池内部铅块简化为6个尺寸为195 mm×600 mm×41 mm的实体单元，核级铅酸蓄电池（带支架）结构计算模型1总计单元数20 711，节点数30 872，模型2总计单元数38 305，节点数52 620，计算模型总重量为4 797.213 kg。钢板采用A3钢，其余钢材采用Q235钢，木材选用红松木，蓄电池壁选用ABS材料。

图4 模型2简化示意图Fig.4 Simplified schematic diagram of Model 2

式中：m为蓄电池中液体总重；m i为i阶模态对流质量；h为蓄电池液面高度；h i为i阶模态对流质量对应高度；b为蓄电池宽度；K i为i阶模态下模拟弹簧的刚度；λ1=1.841,λ2=5.331。

本模型建立基于如下假设：①蓄电池组与周围横梁之间无间隙并考虑摩擦；②考虑蓄电池组与底部槽钢之间的摩擦，摩擦系数通过建模设置接触参数时建立；③蓄电池之间通过塞板固定，塞板与蓄电池之间无间隙；④立柱下部与底部钢板刚性连接，底部过渡钢板及垫木通过锚地螺栓与立柱底部钢板固定；⑤蓄电池底部槽钢与方钢管刚性连接，方钢管通过锚地螺栓与过渡钢板固定；⑥当i=3时，对应的模态对流质量mi仅为液体总重的0.12%左右，可认为对结果影响很小，于是本文中取i=2；⑦模型2中蓄电池的X、Y两个方向的酸液简化均采用EN1998-4—2006中的方法。

结构的地震响应采用谱分析法计算。反应谱分析替代时间-历程分析，主要用于确定结构对时间变化荷载的动力响应情况［7］。地震作用反应谱分析本质上是一种拟动力分析，它首先使用动力方法计算质点地震响应，并使用统计的方法形成反应谱曲线，然后使用静力方法进行结构分析和设计。

2.2 材料本构关系

由于本模型在反应谱作用下始终处于弹性阶段，为降低模型的计算成本，将模型中的材料都简化成理想弹塑性模型。同时为了增强模型的收敛性，材料仅设置弹性阶段参数。其中：A3钢杨氏模量取205.8 GPa，泊松比取0.3；ABS杨氏模量取2.2 GPa，泊松比取0.394；红松木杨氏模量取9 GPa，泊松比取0.45；铅块杨氏模量取17 GPa，泊松比取0.42；橡胶杨氏模量取7.8 MPa，泊松比取0.47。

3 结果分析

3.1 模态分析

通过ABAQUS计算，可得出模型1蓄电池组在X方向的自振频率为50.579 Hz，Y方向的自振频率为80.823 Hz，Z方向的自振频率为86.114 Hz；模型2蓄电池组在X方向的自振频率为14.107 Hz，Y方向的自振频率为21.731Hz，Z方向的自振频率为23.413 Hz，对应的振动模态见图5-图10。与实验结果对比见表2，由表可以看出，模型1与实验结果差距较大，而模型2与实验结果完全吻合，可见壳体-弹簧单元模型的模态分析结果更符合实际情况。

表2 试验与计算自振频率Table 2 Tested and calculated natural frequency

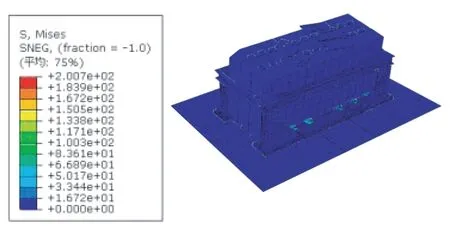
图5 模型1的X向振动模态Fig.5 X-direction vibration mode of model 1

图6 模型2的X向振动模态Fig.6 X-direction vibration mode of model 2

图7 模型1的Y向振动模态Fig.7 Y-direction vibration mode of model 1

图8 模型2的Y向振动模态Fig.8 Y-direction vibration mode of model 2

图10 模型2的Z向振动模态Fig.10 Z-direction vibration mode of model 2

3.2 加速度响应分析

试验模型共有5个加速度测点，分别为MA1-MA5，测点布置图如图11、图12所示。MA1位于蓄电池顶角部，MA2位于支架顶角部，MA3、MA4位于蓄电池中部，MA5位于支架底板角部。

图11 加速度及位移传感器测点布置图（1）Fig.11 Layout of measuring points of accelerometer displacement sensor（1）

图12 加速度及位移传感器测点布置图（2）Fig.12 Layout of measuring points of accelerometer displacement sensor（2）

表3为MA1-MA5测点的试验及有限元模型1、模型2的加速度响应值。

图9 模型1的Z向振动模态Fig.9 Z-direction vibration mode of model 1

由表3可看出：相比模型1，模型2的测点加速度响应值更接近试验结果，模型1仅采用实体单元模拟，与实际情况差距较大。同样，壳体-弹簧单元模型考虑了蓄电池内液体的晃动效应，加速度分析结果更符合实际情况。

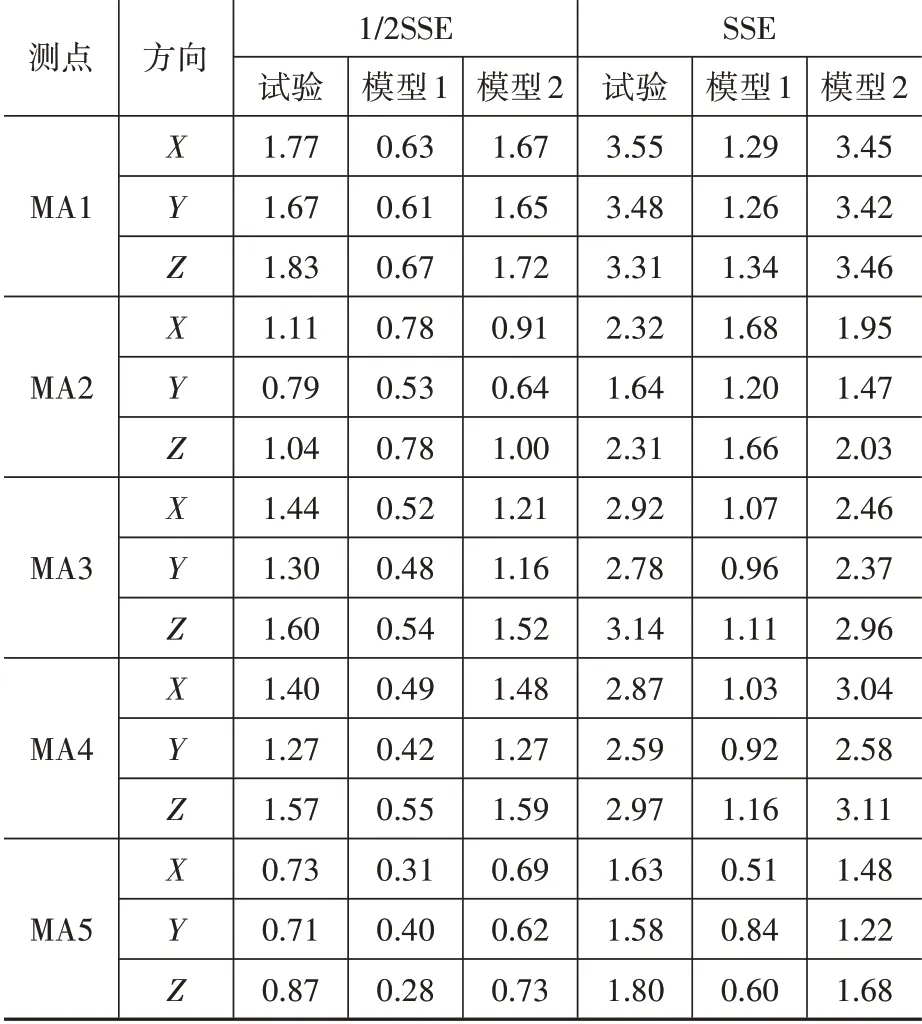
表3 MA1～MA5加速度响应值Table 3 Acceleration response value of MA1～MA5 g

3.3 应变峰值分析

试验模型共有8个应变测点，分别为MS1-MS8，测点布置图如图11-图14所示。MS1、MS4、MS5、MS8位于支架三角板底部中点处，MS2、MS3、MS6、MS7位于支架柱底部中点处。

图13 加速度及位移传感器测点布置图（3）Fig.13 Layout of measuring points of accelerometer displacement sensor（3）

图14 加速度及位移传感器测点布置图（4）Fig.14 Layout of measuring points of accelerometer displacement sensor（4）

表4为MS1-MS8测点的试验及有限元模型1、模型2的应变峰值。

由表4可看出：相比自振频率及加速度响应，模型1与模型2的应变峰值较为接近，且都与试验值误差较小，这与支架应变水平总体较低有关。如果只关注支架的应变峰值，则无论采用哪种建模方式都能得到较为接近的结果。

表4 MS1～MS8应变峰值（με）Table 4 Peak strain of MS1～MS8（με）

4 结 语

以铅酸蓄电池组抗震试验结果为基础，建立了以实体单元模拟蓄电池的有限元模型1及以壳体和弹簧单元模拟蓄电池的有限元模型2，通过谱分析法计算支架的地震反应，并与试验结果进行对比。计算结果表明：①对于结构的自振频率，模型2的结果与试验结果较为吻合，模型1的结果偏差较大；②对于结构的加速度响应值，同样是模型2的结果较符合实际情况；③对于结构的应变峰值，模型1与模型2的结果都与试验值较为接近。

综上所述，在进行带支架的铅酸蓄电池组有限元模拟分析时，壳体和弹簧单元模型能够充分考虑蓄电池在地震时的力学行为，计算结果相对精确、合理，可为类似结构的抗震性能评定提供依据。