多肢钢管-钢管混凝土复合主塔钢混结合段受力性能分析

吴庆雄 李 博 袁辉辉，3，* 黄育凡

（1.福州大学土木工程学院，福州350116；2.福建省土木工程多灾害防治重点实验室，福州350116；3.工程结构福建省高校重点实验室，福州350116）

0 引 言

钢-混结合段是结构中刚度过渡区域，同时承受轴力、剪力和弯矩作用，且钢与混凝土的受力机理不明确，应力复杂［1］。钢-混结合段作为核心受力部件，需要有足够的强度、刚度以及稳定性，且需要良好的耐久性［2］。不当的设计不仅影响整个桥梁结构的受力性能，还会导致钢-混凝土交界面的滑移、钢材的锈蚀以及混凝土的开裂，影响结构的安全性［3］。因此在进行钢-混结合段设计的时候，需要分析其在最不利荷载工况下的应力分布并进行优化，使得结合段处的内力顺畅传递的同时保证其耐久性。

对于钢管混凝土拱桥而言，其拱脚钢-混结合段由钢管拱、管内混凝土、底座混凝土以及其余连接部件组成，存在刚度突变现象，因此该区域受力极为复杂。闫广鹏［4］、李金凯［5］、鲁勤［6］、马雅林［7］、姜自奇［8］、詹刚毅［9］等通过建立三维实体有限元模型的方法，分析了钢管混凝土拱桥拱脚钢-混结合段的应力分布，并提出了相应的结构优化建议。

部分斜拉桥是一种介于斜拉桥和连续梁桥之间的组合体系桥型，由于部分斜拉桥的主梁承担主要荷载，桥塔承担的荷载相对较小，有利于在桥塔构造形式上进行变化，尤其是采用拱形的异形桥塔拥有优美的几何形状而愈发受到青睐，近十年来应用较多［10-12］。本文所研究的主塔钢-混凝土结合段位于某异形桥塔部分斜拉桥的塔底，5根钢管混凝土塔柱相贯在一起，焊接在加劲板上并内嵌于钢筋混凝土塔座中，类似于钢管混凝土拱桥的拱脚段，该结合段结构受力极为复杂。为保证施工和运营过程的结构安全，本文通过有限元软件ABAQUS建立有限元实体模型，对主塔钢-混凝土结合段展开有限元数值分析，明确结合段各部件受力分布和传力模式。

1 工程概况

研究对象为80 m+150 m+80 m的异型主塔部分斜拉桥，是福建平潭综合实验区环岛公路的节点工程。在综合考虑了景观效果、结构受力和水文地质等因素后，该桥主塔设计成了多肢钢管-钢管混凝土复合结构，如图1所示，由5根弧形钢管塔柱旋转组成，钢管内部填充混凝土。钢管之间采用横撑连接，且横撑作为斜拉索的贯通管道。桥塔下部灌注一定高度混凝土，可以抑制塔柱根部塑性铰区域的钢管局部屈曲变形，还可降低主塔结构重心，有利于结构的稳定性。

图1 安海澳大桥主塔塔座示意图（单位：cm）Fig.1 Main tower base of Anhaiao Bridge（Unit：cm）

5根钢管塔柱在塔底处交汇并与塔座锚固。主塔塔座为半椭圆形截面锥形结构，几何上由四分之一的椭圆体与梯形六面体组成。底部截面尺寸12.6 m×9.0 m，塔座高度为12 m。主塔承台为半腰圆形，平面尺寸10.3 m×11.9 m，厚度3.5 m。塔座材料为C45混凝土。5根钢管交汇并相贯于塔座内部，为了增加钢管与底座混凝土接触面积，在钢管外壁设置了剪力钉。为了保证荷载的顺利传递，使塔座应力均匀分布，在钢管底部设置了厚度为50 mm的钢板。为了防止钢板受弯屈曲变形，也为了增大钢板与混凝土底座的接触面积，在钢板底部焊接66块加劲板。

2 精细化实体有限元模型

2.1 几何模型与网格划分

采用有限元软件ABAQUS建立精细化实体有限元模型，在部件中创建弧形钢管塔柱、管内混凝土、混凝土塔座、管底连接钢板以及加劲板。钢管塔柱共有5个，呈对称分布。混凝土塔座为特殊几何形状部件，无法直接创建，因此使用梯形六面体与四分之一椭圆体进行布尔运算的方法建立。由于钢管管径远大于壁厚，采用壳单元模拟钢管。其余部件均采用实体单元进行模拟。5根钢管底部相贯，因此通过布尔运算整合为一个部件。同理，对5根钢管的管内混凝土进行布尔运算，得到管内混凝土整体。如图2所示，钢管塔柱采用四边形壳单元（S4R），管底钢板及加劲板采用六面体实体单元（C3D8R），混凝土采用四面体线性单元（C3D4），通过对网格密度的调整，得到了较好的划分结果。

图2 主塔塔座钢-混结合段实体单元网格划分Fig.2 Solid element meshing for steel-concrete composite segment of main tower base

2.2 边界条件

在全桥有限元模型中，主要考虑了结构恒载、车辆荷载与风荷载的作用，并根据《公路桥梁设计通用规范》（JTG D60—2015）的有关规定计算承载能力极限状态组合作用下的主塔内力。由于主塔塔柱关键截面上的轴力在各项荷载组合的计算中基本保持稳定，综合考虑后选择主塔中塔柱最大弯矩工况作为本文的承载能力最不利荷载工况，同时提取各钢管塔柱的内力施加到钢-混结合段的模型上。

在钢-混结合段实体模型中，按照图3的视角，将钢管混凝土塔柱从左到右依次定义为塔柱1至塔柱5。定义混凝土底座椭圆体底面中心为原点，混凝土底面为XZ平面，Y轴竖直向上。由原点向椭圆底面外侧顶点方向为Z轴，X轴与之垂直，以塔柱5的方向为正向。在钢管混凝土塔柱上表面建立耦合点，并施加荷载，每个点施加的荷载如表1、表2所示。

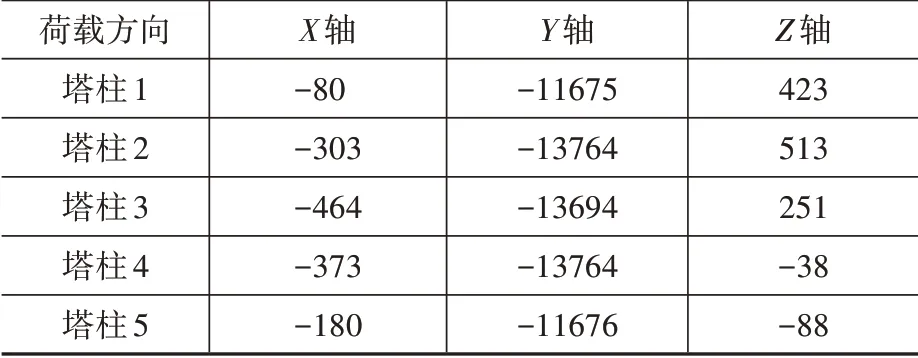
表1 各塔柱耦合点所施加的集中力Table1 Concentrated force exerted by the coupling point of each tower kN

表2 各塔柱耦合点所施加的力矩Table2 Moment exerted by the coupling point of each tower kN∙m

图3 在参考点上施加荷载Fig.3 Load at the reference point

塔座底部完全固定，钢管与管内混凝土、钢管与混凝土塔座采用壳-实体耦合，“硬接触”的方式被用于模拟钢管与混凝土之间的界面法向关系，界面摩擦系数取值为0.6。钢管混凝土底部与管底钢板绑定，管底钢板和加劲板、混凝土塔座相互之间采用绑定约束。

2.3 材料本构关系

本文所研究的钢-混结合段共涉及三种材料：Q345钢材、C40核心混凝土以及C45无约束混凝土。根据《混凝土结构设计规范》（GB 50010—2010）［13］和《钢 结 构 设 计 标 准》（GB 50017—2017）［14］，C40混凝土的弹性模量为32 500 MPa，C45混凝土的弹性模量为33 500 MPa，二者泊松比均为0.2；Q345钢材的弹性模量为206 000 MPa，泊松比为0.3。

2.3.1 钢材

在ABAQUS软件中，使用弹塑性模型来描述钢材的本构关系，该模型假设钢材等向强化。低碳钢的理想应力-应变关系曲线包含弹性段、弹塑性段、塑性段、强化段与二次塑流段5个阶段。如图4所示，本文所采用的钢材本构关系为文献［12］提出的四折线模型，该模型中省略了应力-应变曲线中较短的弹塑性段。

图4 钢材的应力-应变关系Fig.4 Constitutive relation of steel

2.3.2 无约束混凝土

塔座混凝土为无约束混凝土，可采用现行的《混凝土结构设计规范》（GB 50010—2010）［10］所提供的计算模型，如图5所示。其单轴受压和单轴受拉的应力-应变关系计算式可参见文献［10］的有关规定，在此不再赘述。

图5 普通混凝土的应力-应变关系Fig.5 Constitutive relation of ordinary concrete

2.3.3 钢管内核心混凝土

对于钢管内核心混凝土，本文采用文献［15］提出的约束混凝土受压本构关系，如图6（a）所示，图中各特征值按照式（1）-式（11）计算。

图6 钢管内核心混凝土的应力-应变关系Fig.6 Constitutive relation of core concrete in steel tube

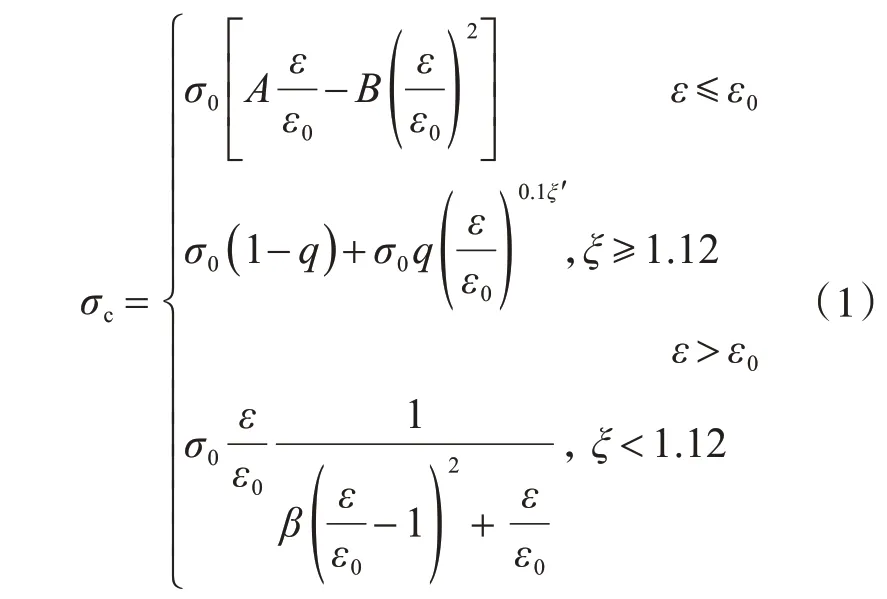
式中：εc为普通混凝土应力-应变关系曲线峰值点对应的应变；ε0和σ0为核心混凝土应力-应变关系曲线第一段与第二段连接点的应变与应力；ξ为套箍系数；ξ′为修正后的套箍系数；ke为偏心纠正系数。

图6 （b）为管内核心混凝土受拉应力-应变关系曲线，该模型假设开裂前混凝土处于弹性状态，开裂后混凝土的应力状态采用式（12）计算。

式中，εt0和σt0为普通混凝土开裂应变与应力。

在ABAQUS中常采用混凝土损伤模型来描述混凝土的本构关系，该模型可以考虑混凝土的初始裂缝以及受力过程中损伤的累积而导致的裂缝发展。与其他材料不同的是，该模型在定义了应力-应变关系之外，还需要定义损伤因子与非弹性应变的关系。损伤因子采用下式计算：

3 塔座钢混结合段受力性能分析

3.1 整体分析

3.1.1 应力分析

为直观了解主塔钢-混结合段局部实体模型的应力分布情况，在后处理中查看模型计算结果的整体应力云图，如图7所示。钢管最大应力出现在塔柱3（中塔柱）与塔柱2和塔柱4（次塔柱）的相贯处。该点附近出现了较为明显的应力集中现象，这可能是由于中塔柱与次塔柱之间的距离相对较小，中塔柱底部钢管被相贯截取部分过多导致的。

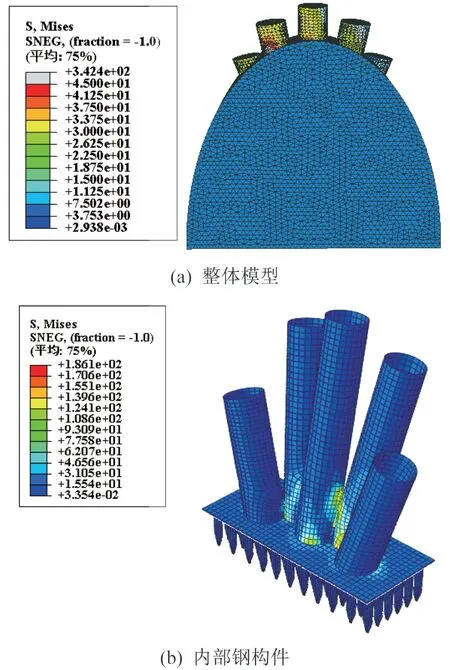
图7 主塔钢-混凝土结合段应力云图（单位：MPa）Fig.7 Stress nephogram of steel-concrete composite segment（Unit：MPa）

从整体上来看，钢管整体未发生屈服。而混凝土塔座受力较小，混凝土未开裂破坏。该钢-混凝土结合段满足受力性能要求，构造合理。

3.1.2 变形分析

为了直观了解主塔钢-混结合段的变形情况，在后处理中查看模型的整体变形图，如图8所示。最大变形在中塔柱的顶部远离底座一侧，值为61.84 mm。这是由于塔柱顶部为自由端，且外荷载的方向偏向此处导致的。混凝土塔座及塔座中部件的变形量较小，整体变形连续协调，变形量满足设计要求。

图8 主塔钢-混凝土结合段变形图（单位：mm）Fig.8 Deformation diagram of steel-concrete composite segment（Unit：mm）

3.2 局部分析

3.2.1 钢管混凝土塔柱

为更加清晰地了解钢管混凝土塔柱的应力分布情况，提取钢管混凝土塔柱应力云图，如图9所示。所有塔柱底部的钢管应力较大，在两根钢管相贯处存在应力集中现象，最大值为186.1 MPa，钢管均未发生屈服，受力性能良好。

图9 钢管混凝土应力云图（单位：MPa）Fig.9 Stress nephogram of CFST（Unit：MPa）

在最不利荷载作用下，管内混凝土在靠近底座混凝土椭圆体侧受压，靠近梯形六面体侧受拉。管内混凝土大部分处于受压状态，最大压应力值为32.5 MPa，混凝土未发生压碎现象。与钢管类似，在5根管内混凝土柱之间也存在相贯线处出现的应力集中现象。该点拉应力较大，可能导致该点混凝土的开裂破坏。建议在钢管之间相贯的部分加强焊缝的强度，并考虑额外的加固措施。

除应力集中的点外，其余管内混凝土的受拉应力均小于5 MPa，混凝土未发生开裂。管内混凝土整体满足设计受力要求，构造合理。

3.2.2 管底钢板

由图10可知，管底钢板的Mises应力由边缘至中心逐渐增加，这是由于钢管混凝土塔柱将其上部荷载传递到底部，从而管底钢板与钢管塔柱连接区域应力较大。最大应力位于钢管3底部，其值为54.2 MPa，这也是由于在钢管3上面施加的荷载最大导致的。管底钢板未发生屈服，满足设计受力要求，构造合理。

图10 管底钢板应力云图（单位：MPa）Fig.10 Stress nephogram of steel plate（Unit：MPa）

3.2.3 加劲板

管底钢板下表面焊接加劲板，共66个。整个加劲板群的应力云图如图11（a）所示。应力最大点所在的加劲板位于中塔柱和次塔柱交界处，与管底钢板上最大应力点的位置对应。在加劲板群中，最外侧一圈的加劲板所受应力较小（单个加劲板中最大应力不超过10 MPa），在结构中的作用不明显，可以考虑结构优化措施。

图11（b）为应力最大的加劲板应力云图，其应力自顶端向下逐渐减小，最大应力值为177.8MPa，位于加劲板顶端靠近中塔柱一侧。整个加劲板群均未发生屈服，加劲板满足设计受力要求，构造合理。

图11 加劲板应力云图（单位：MPa）Fig.11 Stress nephogram of stiffening plate（Unit：MPa）

3.2.4 混凝土塔座

由图12可知，混凝土塔座以受压为主，压应力在0.72～1.63 MPa，塔座所受的荷载一部分来自钢管混凝土塔柱侧面对它的传递荷载，另一部分是钢管混凝土塔柱对管底钢板的荷载，再由管底钢板传递到混凝土塔座上。

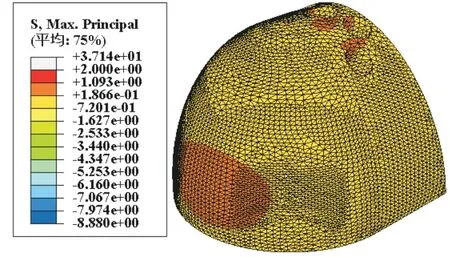
图12 混凝土塔座应力云图（单位：MPa）Fig.12 Stress nephogram of concrete tower base（Unit：MPa）

由应力云图可知，混凝土塔座与钢管塔柱侧面所连接的区域受力均衡，且未出现应力集中现象。但在管底钢板及加劲板区域出现了应力集中的现象，该处混凝土被加劲板分割成了许多孤立的区域。而在实际结构中，加劲板周围区域设置了钢筋进行连接，钢筋的存在可以加强该处混凝土的整体性，并可以承担一部分应力，大幅缓和此处的应力集中。此外，在塔座背面及塔柱预留孔顶部存在拉应力，且最大拉应力未超过2 MPa。

因此在不考虑管底钢板区域应力集中点的情况下，混凝土塔座整体受力较小，且未发生破坏。混凝土塔座满足设计受力要求，构造合理。

4 结 论

以多肢钢管-钢管混凝土复合主塔部分斜拉桥为工程背景，对其主塔底部钢-混结合段进行有限元建模分析，主要结论如下：

（1）钢-混结合段在实桥最不利荷载工况下，整体受力较为均衡，变形连续协调。

（2）在钢-混结合段中，来自钢管顶部的外荷载小部分通过钢管侧壁传递到混凝土塔座中，而大部分荷载则通过钢管底部传递到管底钢板上，再由管底钢板及加劲板传递到混凝土塔座中。

（3）钢管塔柱3与塔柱2、塔柱4之间距离过小，导致其圆形截面被裁切部分较大，从而在其相贯线上易出现应力集中现象。

（4）混凝土塔座上部受力均衡，混凝土未出现开裂或压碎现象，但混凝土塔座底部被管底钢板及加劲板割裂，易出现应力集中现象。建议在此处设置大量钢筋进行整体连接，并考虑加劲板群的整体结构优化。