多跨长联连续梁桥考虑行波和碰撞效应的位移响应研究

赵 洋 熊柏林 徐略勤，* 王 佩

（1.重庆交通大学土木工程学院，重庆400074；2.中国市政工程西南设计研究总院有限公司，成都610000）

0 引 言

为了改善行车舒适性，减少伸缩缝数量，连续梁桥的连续跨数随着技术的进步逐渐增多，多跨长联连续梁桥在公路和城市交通中屡见不鲜。这类桥梁通常在纵向仅设一个固定墩，其余均为活动墩。在地震作用下，主梁的纵向惯性力大部分聚集在固定墩上，导致固定墩出现很大的塑性变形甚至破坏，带动主梁在活动墩和伸缩缝处产生显著的相对位移，并在伸缩缝处引起邻梁之间的碰撞现象。连续跨数的增多使得上述问题更加突出。此外，由于纵向跨度大，地震波到达各个桥墩的时间不一致，由此产生的行波效应［1］有可能进一步加剧上述问题。

近年来，针对桥梁结构行波效应、结构碰撞等问题的研究已有较丰富的积累，如在行波效应方面，魏凯等［2］以多跨长联组合桥为背景，利用绝对位移法探讨了不同行波激励工况对地震响应的影响规律；何浩祥等［3］通过对多跨连续梁桥不同支点施加异向及不同幅值的激励，研究了跨数对连续梁桥多点激励地震响应的影响；李小珍等［4］以刚构-连续组合梁桥为背景工程，采用大质量法进行多点地震激励，研究了相位差对桥梁非线性地震响应的影响；陈士通等［5］研究了行波效应对梁桥墩顶锁死销减震性能的影响；刘正楠等［6］以简支+连续高速铁路桥梁为研究对象，对比了行波效应对延性、减隔震两种抗震体系的影响。在碰撞效应方面，王军文等［7］认为多联连续梁桥相邻联的周期比和周期大小是影响结构碰撞效应的关键；李忠献等［8］研究了地震动空间效应、土-基础相互作用对多跨连续梁桥临界碰撞间隙的影响；许祥等［9］基于Kelvin模型和Hertz-damp模型构造出用于模拟结构间相互碰撞的新碰撞函数，并通过碰撞实验对其准确性进行了验证；沙奔等［10］以碰撞次数和碰撞力为指标，探究了地震动频谱特性和地震动峰值加速度对结构碰撞效应的影响。可以看到，现有研究的对象和角度很多，成果也很丰富，但主要针对行波和碰撞效应中的一个问题进行探讨，将两者结合起来研究的相对较少，典型的如Zheng等［11］以主梁和桥台间的碰撞为研究对象，对比了行波效应与一致激励的区别；而针对多跨长联连续梁桥行波和碰撞效应的研究则更为鲜见。前文指出多跨长联的结构布置形式很可能导致这两种效应更加突出，对桥梁的抗震安全产生重大的隐患。

本文以某跨黄河的长联多跨连续桥为例，在考虑行波效应的基础上，采用参数分析法探讨伸缩缝间隙、碰撞刚度、活动支座摩擦系数等因素对桥梁关键地震位移响应的影响规律，并据此提出多跨长联连续梁桥的抗震策略，以期为同类桥梁的抗震提供参考。

1 基本理论与分析方法

1.1 行波效应分析理论

行波效应的分析方法一般可分为时域分析法和频域分析法两类，前者包括大质量法、大刚度法、绝对位移法、拉格朗日乘子法等常用方法，后者则包括随机振动法、虚拟激励法等。时域分析法计算原理简单，能够较为精确地描述结构非一致地震响应的全过程，且便于商用有限元软件的建模操作。本文基于SAP2000软件采用时域分析法，按照绝对位移法求解，如图1所示，即：对结构各支承点直接指定其各自位移时程函数，根据地震波的传播速度（即视波速）得到各时程函数的时滞效应，以此进行行波效应分析。对于多跨长联连续梁桥来说，由于横桥向跨度较小，所以无须考虑横桥向行波效应的影响，即只考虑纵桥向行波效应。

图1 行波效应示意图Fig.1 Schematic diagram of traveling wave effect

1.2 结构碰撞分析方法

在地震中，相邻结构发生的碰撞现象会导致梁体局部发生塑性变形，甚至出现局部破坏。在多跨长联连续梁桥中，由于上部结构自重大、惯性力集中，因此梁端伸缩缝处的碰撞效应尤其剧烈。在全桥有限元分析中，通常采用接触单元法模拟碰撞效应，如图2所示。当相邻梁体相互接触时，接触单元被激活，碰撞发生；当相邻梁体分离后，接触单元被钝化，其数学表达式为

图2 碰撞效应示意图Fig.2 Schematic diagram of pounding effect

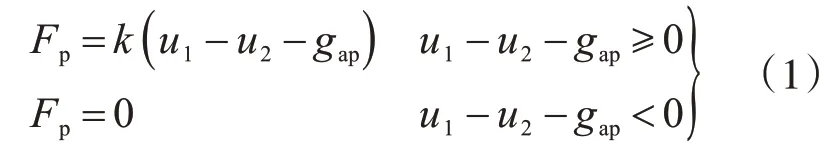
式中：Fp表示结构碰撞力；k表示碰撞刚度；u1、u2分别表示两相邻梁体的位移；gap表示两相邻梁体的初始间距，即梁端伸缩缝的大小。

2 背景工程与分析模型

2.1 桥梁概况

某跨黄河长联多跨连续桥跨径布置为（60+5×90+60）m，如图3（a）所示。主梁为单箱单室预应力混凝土连续梁，梁高由支点处5m逐渐变为跨中2.2 m，梁底曲线采用二次抛物线变化，箱梁顶宽14 m、底宽7 m，如图3（b）、（c）所示。下部结构采用实体式桥墩，墩身分别为3.5 m×7 m和3 m×7 m的矩形截面，从1#墩到8#墩，墩高分别为20.2 m、18.5 m、21.0 m、19.0 m、18.5 m、20.0 m、19.5 m、13.9 m。除5#固定墩的承台尺寸为16.85 m×15.65 m×3.0 m外，其他中间墩的承台均为16.85 m×11.0 m×3.0 m，1#、8#过渡墩的承台尺寸为6.4 m×16.2 m×2.5 m。支座采用JQGZ（Ⅱ型）系列抗震球钢支座，除5#墩采用固定支座外，其余各墩均采用单向活动支座，如图3（d）所示。固定墩、活动墩和过渡墩的桩基分别为14ϕ1.8 m、10ϕ1.8 m、8ϕ1.5 m钻孔灌注桩。主桥的东、西岸引桥均为5×30 m预应力混凝土简支梁。

图3 桥例示意Fig.3 Bridge layout

2.2 有限元建模

采用SAP2000建立有限元模型，主梁、盖梁、墩柱均采用线弹性梁单元模拟，由于主梁为变截面连续梁，所以主梁节点建立在相应段主梁形心位置处；抗震球钢支座采用解耦弹簧单元分别模拟其纵向、横向、竖向的刚度，其中，水平活动方向采用简化双线性滞回本构关系，其他方向采用线性本构关系，如图4所示；主桥与东、西岸引桥在伸缩缝处的碰撞现象采用图2所示的接触单元模拟；桩基础采用6×6集中土弹簧模拟桩-土相互作用效应，并根据m法计算弹簧刚度系数；考虑到混凝土桥墩墩底在地震力作用下会形成塑性铰，采用Multilinear Plastic单元模拟塑性铰区的弯矩-转角（M-θ）关系，建立背景桥例的全桥有限元分析模型，如图4所示，图中只显示了主桥部分的模型，东、西两侧引桥未予以显示。在后文进行时程分析时，桥梁结构体系阻尼采用Rayleigh模型，阻尼比根据规范［1］取5%。

图4 有限元模型示意图Fig.4 Illustration of finite element model of the bridge

2.3 分析工况

由于行波效应和碰撞效应的机理很复杂，很难确定各个参数的精确取值，一般都需要进行参数对比分析。其中，视波速是行波效应的关键影响因素，初始间隙、碰撞刚度是碰撞效应的关键影响因素。考虑到温度变化会导致主梁伸缩，引起伸缩缝初始间隙发生改变，同时考虑到碰撞现象发生的概率，因此本文选择4～12 cm作为伸缩缝初始间隙的变化区间。而本文重点探讨桥梁结构的地震位移响应，因此球钢支座的摩擦系数也作为变化参数进行分析。表1列举了本文的分析工况及其对应的参数取值情况，其中基准工况取值如下：初始间隙为8 cm，碰撞刚度取1.5×106kN/m，支座摩擦系数取0.03，其余各工况在基准工况基础上进行改变。

表1 分析工况设置Table 1 Details of analytical cases

3 场地地震活跃性

根据工程场地地震安全性评价，桥例的抗震设防烈度为Ⅷ度，场地类别为Ⅱ类，50年超越概率为2%的设计加速度反应谱Sa（T）为Sa(T)=

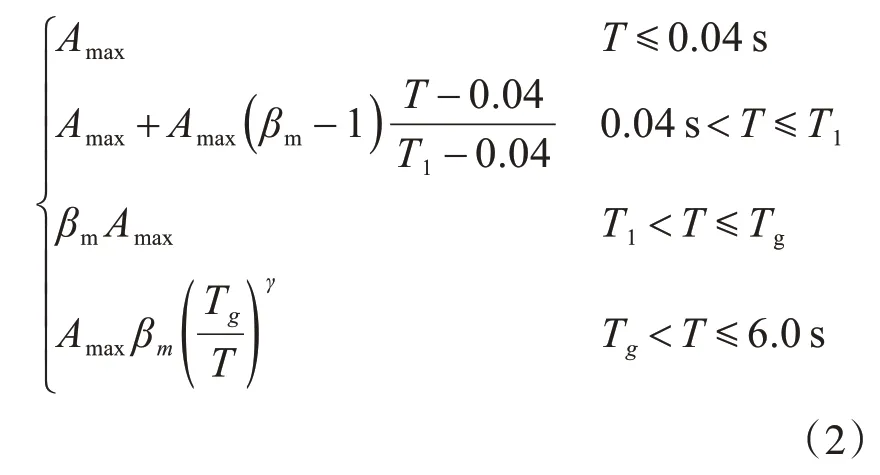
式中：Amax为地表水平设计加速度峰值，取值为0.414g；βm反应谱放大系数最大值，取值为2.4；T1为反应谱起点周期，取值为0.17 s；Tg为反应谱起点周期，取值为0.50 s；γ为衰减指数，取值为0.9。

根据式（2）的设计反应谱，从太平洋地震工程中心（PEER）匹配7条实际地震动记录，并将7条地震波的峰值加速度统一调整为0.414g，将其编号为No.1-No.7。图5（a）、（b）为典型加速度时程曲线与其相对应的实际位移时程，图5（c）为7条实际地震动反应谱与设计反应谱的对比情况。在非线性时程分析中，地震动输入采取纵向+竖向的方式，输入函数为位移时程曲线，除特殊说明外，以下结果均为7条地震波的平均值。

图5 地震动Fig.5 Ground motions

4 位移响应参数分析结果

4.1 梁端位移响应

图6为不同视波速、不同初始间隙下的梁端位移响应分析结果。由图6（a）可见，在不考虑行波效应时，主桥梁端位移随着伸缩缝初始间隙的增大而缓慢下降，如初始间隙从4 cm增至12 cm时，主桥西岸梁端位移下降了3.1%，东岸梁端位移下降了2.5%；当考虑行波效应时，主桥梁端位移随初始间隙的变化规律出现了相反的趋势，即可能随着初始间隙的增大而缓慢增大，尤其当视波速较小时（600～1 500 m/s），如当视波速为1 000 m/s时，主桥西岸梁端位移从初始间隙为4 cm时的12.75 cm增至初始间隙为12 cm时的13.24 cm，增幅为3.8%，东岸梁端位移则从12.56 cm增至12.99 cm，增幅为3.4%。值得注意的是，当视波速较小时，主桥梁端位移在数值上低于一致激励时的位移，随着视波速的增大，考虑行波效应的主桥梁端位移逐渐接近并最终超过了一致激励的结果。由图6（b）可见，不管是否考虑行波效应，引桥梁端位移总体上都随着伸缩缝初始间隙的增大而增大，且视波速越大，考虑行波效应的引桥梁端位移越接近一致激励时的结果；从增幅来说，在一致激励时，引桥西岸梁端位移从初始间隙为4 cm时的17.02 cm增至初始间隙为12 cm时的18.78 cm，增幅为10.3%，东岸梁端位移则从18.65 cm增至20.82 cm，增幅为11.6%，而考虑行波效应的引桥梁端位移随初始间隙的增幅也基本类似，不再赘述。由图6（c）可见，与主桥、引桥各自的梁端位移响应不同，考虑行波效应后，主桥和引桥梁端的相对位移（与碰撞程度直接相关）明显高于一致激励的结果，且视波速越小，行波效应的影响越大，如当视波速为600 m/s时，西岸相对梁端位移比一致激励结果最大增大了59.9%（对应的初始间隙为4cm），东岸相对梁端位移则最大增大了19.1%（对应的初始间隙为4cm）；此外，随着伸缩缝初始间隙的增大，不管是否考虑行波效应，东、西两岸的梁端相对位移均不断增大。

图6 工况C1梁端位移响应Fig.6 Girder end displacement responses in cases C1

整体来看，考虑行波效应可能会降低单侧梁端的地震位移响应，且视波速越小，降幅越大，但主、引桥梁端相对位移却呈相反规律，即行波效应会增大其数值，且视波速越小，增幅越明显。其原因可能是行波效应加剧了主桥和引桥的不同步振动，伸缩缝的初始间隙越大，这种不同步振动的自由度越高，从而使主、引桥梁端相对位移不断增大，而单侧梁端的最大位移容易受到碰撞效应的限制，反而有所下降。另外，视波速越小，地震波到达各桥墩的时间差越长，主、引桥的不同步振动可能越明显。

图7给出了梁端位移响应随视波速和碰撞刚度的变化曲线。由图7（a）可见，在不考虑行波效应时，随着碰撞刚度的增大，主桥梁端位移先逐渐增大然后进入平台，最大增幅为4.7%，转折点所对应的碰撞刚度为1.5×106kN/m；当视波速较大（≥1 500 m）时，考虑行波效应后，主桥梁端位移随碰撞刚度的变化规律与一致激励基本一致，数值上也接近；但在视波速较小时（600～1 000 m/s），行波效应明显会降低主桥梁端位移响应，如当视波速为600 m/s时，西岸主桥梁端位移相比一致激励时最大减小了8.9%，东岸则最大减小了10.6%。由图7（b）可见，不管是否考虑行波效应，引桥梁端位移都随着碰撞刚度的增大而下降，且随着视波速的增大，考虑行波效应的结果逐渐趋近一致激励的结果，尤其在东岸侧位移基本与一致激励时相等。由图7（c）可见，考虑行波效应后，主桥和引桥梁端的相对位移明显高于一致激励的结果，尤其当视波速较小时，如当视波速为600 m/s时，西岸相对梁端位移比一致激励结果最大增大了56.6%（对应的碰撞刚度为1.5×108kN/m），东岸相对梁端位移则最大增大了11.6%（对应的碰撞刚度为1.5×106kN/m）；随着碰撞刚度的增大，东、西两岸的梁端相对位移均不断下降，一致激励时最大下降了26.7%，考虑行波效应时最大下降了24.3%。需要说明的是，碰撞刚度的增大尽管会减小梁端相对位移，但同时也会导致碰撞力的增大，限于篇幅本文没有列出相应的结果，后文会有进一步的交代。

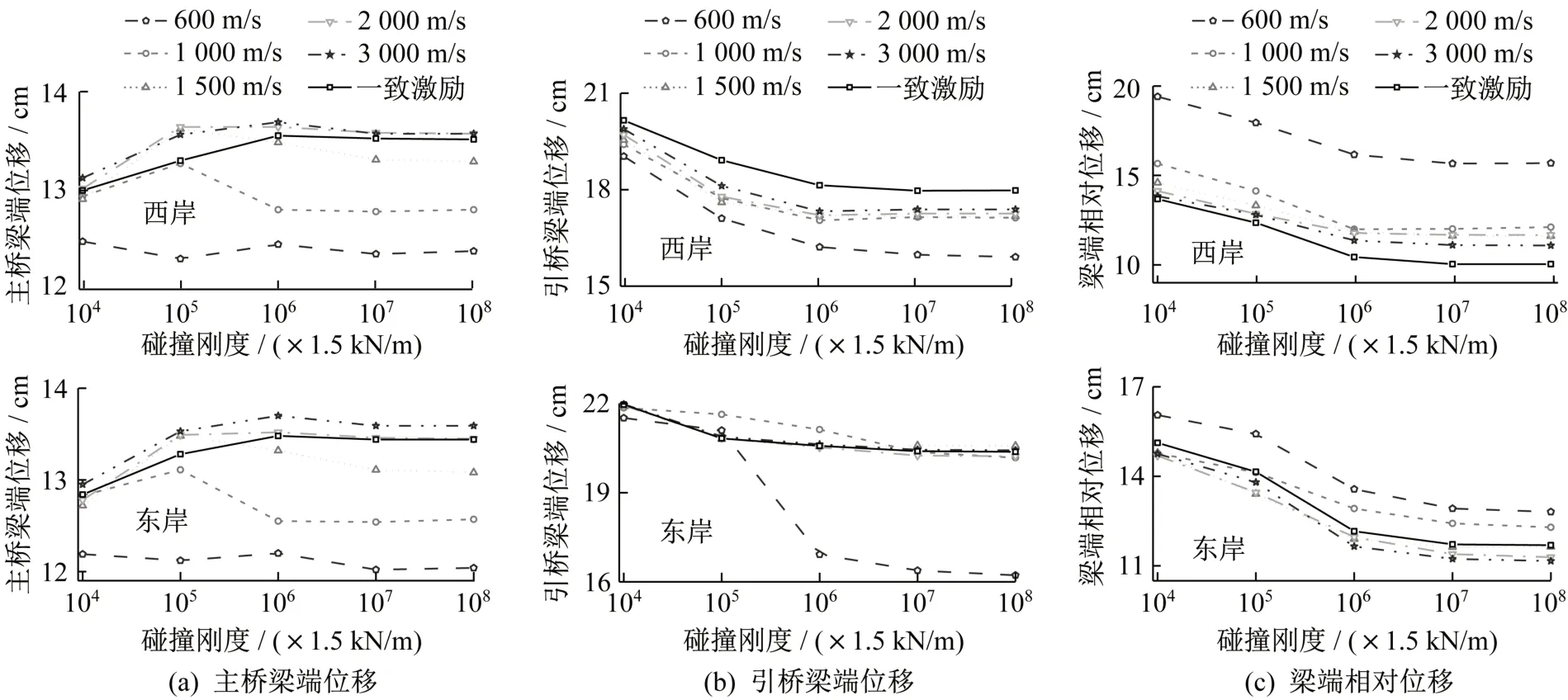
图7 工况C2梁端位移响应Fig.7 Girder end displacement responses in cases C2

图8为梁端位移响应随视波速和支座摩擦系数的变化规律曲线。可以看到，随着支座摩擦系数的增大，主桥梁端位移不断减小，引桥梁端位移受碰撞效应的影响小幅增大；在不考虑行波效应时，主桥和引桥梁端的相对位移在东、西两岸表现为大致相反的规律，其中西岸的相对位移随摩擦系数的增大而逐渐增大，东岸则相反。从行波效应的影响规律来看，总体来说，行波效应会导致主桥和引桥各自梁端位移明显下降，但会导致主桥和引桥梁端的相对位移明显增大，尤其在视波速较小的情况下，其原因如前文所述。从数值上来看，当视波速为600 m/s时，主桥西岸梁端位移相比一致激励时最大减小了13.2%（对应的摩擦系数为0.05），东岸最大减小了14.1%（对应的摩擦系数为0.05）；引桥西岸梁端位移相比一致激励时最大减小了15.3%（对应的摩擦系数为0.05），东岸最大减小了20.2%（对应的摩擦系数为0.05）；而主桥和引桥梁端的相对位移最大增大了77.8%（西岸，对应的摩擦系数为0.01），15.2%（东岸，对应的摩擦系数为0.05）。需要说明的是，本文由于将研究重点放在主桥上，因此仅改变了主桥抗震球钢支座活动方向的摩擦系数，引桥所采用的板

图8 工况C3梁端位移响应Fig.8 Girder end displacement responses in cases C3

式橡胶支座并未进行参数变化，因此引桥梁端相对位移的变化主要由碰撞效应引起。实际上，板式橡胶支座的摩擦系数在地震中也会发生一定程度的改变［12］，其对本文结论的影响还有待于进一步研究。

4.2 支座位移响应

图9 为行波效应和伸缩缝初始间隙对支座位移响应的影响规律（分别对应东、西两岸过渡墩处的主桥支座和引桥支座，下文同）。可以看到，初始间隙的大小对主桥支座位移响应的影响并不大，且东、西两岸支座的变化规律不同，支座位移变幅在一致激励下分别为7.14～8.2 cm（西岸）、8.51～8.94 cm（东岸），在视波速为600 m/s的行波效应下分别为10.18～13.73 cm（西岸）、7.72～8.14 cm（东岸）。不管是否考虑行波效应，引桥东、西两岸支座位移响应曲线的变化规律基本一致，即随着初始间隙的增大而增大。与梁端位移不同的是，考虑行波效应后，主桥西岸支座的位移响应增大了，且增幅非常明显，在视波速为600 m/s时最大增大了67.4%（对应的初始间隙为12 cm），随着视波速的增大，支座位移响应逐渐接近一致激励的结果；主桥东岸支座的位移响应在考虑行波效应后减小了，但不同的是视波速的影响规律不如之前那么显著。行波效应对引桥支座位移响应的影响规律与前文梁端位移比较接近，不再赘述。

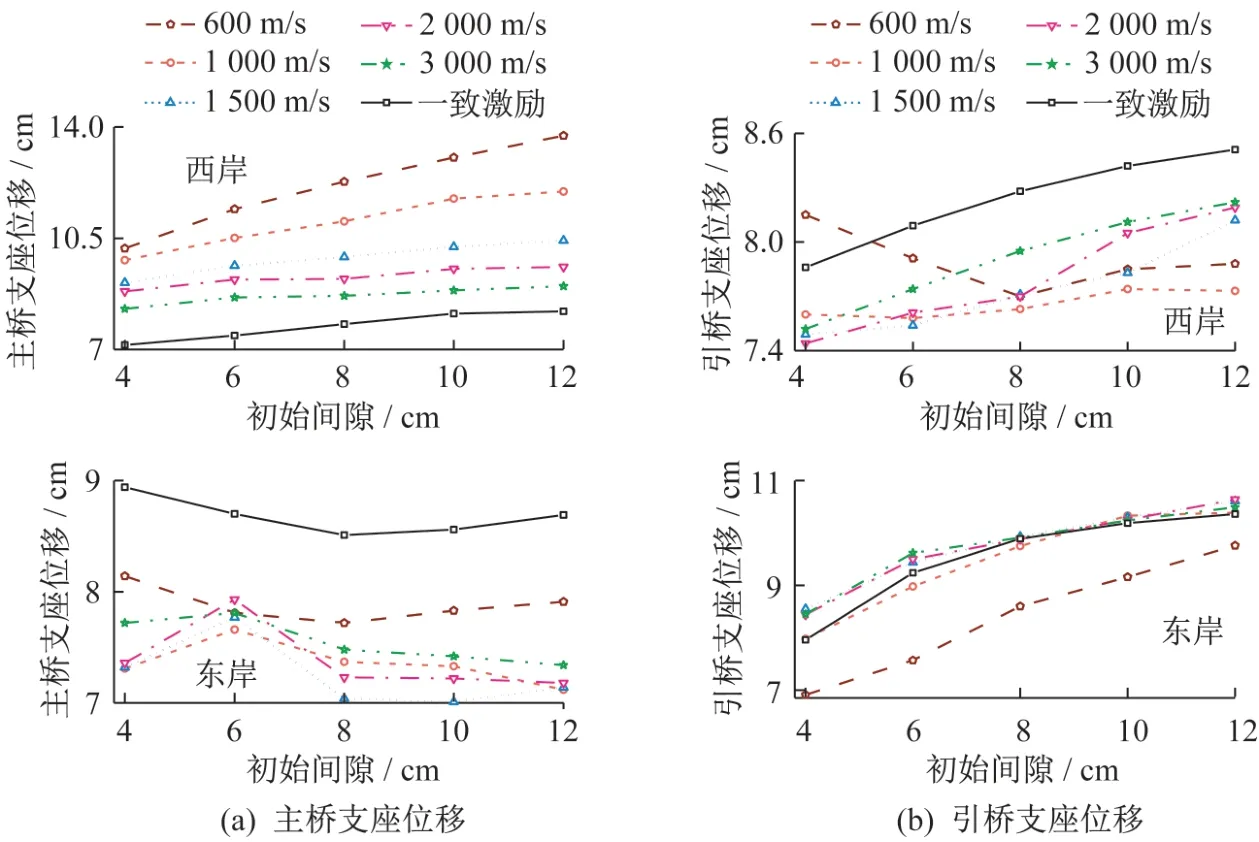
图9 工况C1支座位移响应Fig.9 Bearings displacement responses in cases C1

由图10可见，碰撞刚度对主桥东、西两岸支座位移响应的影响规律不一致，但对引桥东、西两岸支座位移响应的影响规律一致。总体来说，随着碰撞刚度的增大，支座位移响应趋于减小，如在不考虑行波效应时，主桥西岸支座的位移响应随碰撞刚度的增大减小了14.4%，东岸支座先增后减，最大变幅为9.9%；引桥西岸支座减小了11.5%，东岸支座减小了16.6%。与图9的规律类似，行波效应会增大主桥西岸支座的位移响应，而减小其他几个支座的位移响应。总体来说，行波效应的影响不容忽视，会导致主桥西岸支座的位移响应最大增大80.0%（视波速为600 m/s且碰撞刚度为1.5×104kN/m）。

图10 工况C2支座位移响应Fig.10 Bearings displacement responses in cases C2

图11 为行波效应和支座摩擦系数对支座位移响应的影响规律。由图可见，随着摩擦系数的增大，4个支座的位移响应均不断减小，其中主桥支座的减小幅度非常明显，比如在不考虑行波效应时，西、东岸支座的最大减幅分别达28.0%、32.9%；而引桥支座位移响应的减小主要由碰撞效应引起，其摩擦系数在本文分析中并没有进行参数变化，因此可以看到其位移变化幅度相对主桥支座小得多。与图9、图10类似，行波效应会增大主桥西岸支座的位移响应，而减小其他几个支座的位移响应，且行波效应的影响幅度不容忽视，如对于主桥西岸支座而言，当视波速为600 m/s时，行波效应最大可使其位移响应增大71.1%（对应的摩擦系数为0.05）。

图11 工况C3支座位移响应Fig.11 Bearings displacement responses in cases C3

5 减碰与抗震措施分析

前文的分析结果表明，行波效应会增大主、引桥梁端相对位移，且视波速越小，增幅越大，其原因可能是主、引桥之间非不同振动加剧了伸缩缝处的碰撞现象。为了进一步探讨这个问题，并减轻碰撞效应的不利影响，本节针对背景工程的结构特点，通过对背景桥例的支反力进行了计算，并参考原球钢支座型号，提出采用高阻尼隔震橡胶支座代替原抗震球钢支座，高阻尼橡胶支座具有饱满的滞回耗能曲线，且震后残余变形较小。高阻尼橡胶支座构造及其双线性恢复力模型如图12所示，图中，Kp、Kc、Keff分别代表支座的初始刚度、屈服刚度、等效刚度，Qy、Xy代表屈服力与屈服位移。根据规范［13］，选取高阻尼橡胶支座的设计参数如表2所示。

图12 高阻尼橡胶支座Fig.12 High damping rubber bearings

表2 高阻尼橡胶支座设计参数Table 2 Design parameters of high damping rubber bearings

将背景工程过渡墩支座替换为HDR（Ⅰ）-470×570型高阻尼橡胶支座，将主桥上固定支座、活动支座全部设置为HDR（Ⅰ）-1170×1170型高阻尼橡胶支座，形成减震分析工况，并将之与基准工况进行对比。两个工况的伸缩缝初始间隙、碰撞刚度均为8cm和1.5×106kN/m，基准工况的球钢支座摩擦系数取0.03。前文分析表明，当视波速为600 m/s时，行波效应的影响最为不利，因此本节按视波速为600 m/s来考虑行波效应的影响。

图13以No.2地震波为例给出了两种工况下的地震响应情况。由图13（a）可见，相较于原始工况，减震体系的碰撞力普遍减小，碰撞力峰值在西岸和东岸分别减小17.4%、11.6%；由图13（b）可见，除东岸相对位移略有增大外（增幅为5.2%），其余各位移响应均有不同程度的减小，减震体系对减小西、东岸主桥梁端位移的效果尤为显著，相比原始工况分别减小了48.7%、41.9%。由图13（c）可见，对于各墩底弯矩而言，相比原始工况，减震工况对2#墩、4#墩、6#墩、7#墩弯矩值有不同程度的增大效果，增幅范围为18.6%～38.3%，对各墩墩底剪力的影响与弯矩类似。对于5#固定墩而言，原始工况的墩底弯矩、剪力分别是减震体系的2.5倍、2.1倍，即地震力高度集中于固定墩处。由此可见，尽管背景工程的原始设计中采用了抗震球钢支座，但由于固定墩的设置，导致多跨长联主梁的惯性力高度集中于5#固定墩，而其余各墩的抗震能力没有得到完全发挥，地震力分配非常不均匀，其后果是固定墩可能完全破坏，而其余活动墩的抗震潜力又得不到发挥。采用高阻尼橡胶支座后，全桥地震力分配更趋均匀，1～8#墩的最大弯矩/最小弯矩比为1.57，最大剪力/最小剪力比为2.19，而原始工况的最大弯矩/最小弯矩比为3.99，最大剪力/最小剪力比为3.72。减震工况大幅降低了固定墩的抗震需求，可有效降低其倒塌风险，小幅增大了各活动墩的抗震需求，有利于发挥其抗震潜力，使全桥抗震的冗余度得到提升。图13（c）也可以解释图13（a）、（b）的结果，由于原始工况设置了固定墩，多跨长联主梁的惯性力主要由固定墩承担，使得固定墩发生了严重的塑性变形，从而导致主梁的纵向位移反而很大；而设置高阻尼橡胶支座后，尽管没有固定墩，但各个墩的位移接近，均没有出现严重的塑性变形，主梁的位移主要由橡胶支座变形产生，而高阻尼橡胶支座具有较好的恢复力机制，因此主梁的位移反而比原始工况低，从而降低了碰撞效应。

图13 减碰效果对比Fig.13 Comparisons of pounding mitigation effects

6 结 论

本文主要结论如下：

（1）行波效应趋向于减小主桥和引桥的梁端位移，但会大幅增大主桥、引桥的梁端相对位移，且视波速越小，上述规律越明显，其原因是行波效应加剧了主桥、引桥之间的非一致振动现象，导致碰撞效应更加突出。

（2）行波效应对过渡墩各个支座位移的影响主要以减小为主，但会增大主桥西岸支座的位移响应，且视波速越小，不利影响越大，最大增幅高达80.0%，不可忽略。

（3）伸缩缝初始间隙的增大会增大主桥、引桥的梁端相对位移，最大增幅为37.1%；碰撞刚度的增大会减小主桥、引桥的梁端相对位移，最大减幅为26.7%；支座摩擦系数的增大也会减小主桥、引桥的梁端相对位移，最大减幅为18.7%。

（4）伸缩缝初始间隙的增大趋向于增大过渡墩各个支座的位移响应，最大为41.2%；碰撞刚度的增大会减小各个支座的位移响应，最大减幅为29.5%；支座摩擦系数的增大会减小主桥支座的位移响应，最大减幅达32.9%。

（5）采用高阻尼橡胶支座后，伸缩缝处的碰撞力峰值明显减小，最大减幅为17.4%；主桥梁端位移响应大幅减小，最大减幅达48.7%，其余梁端位移响应也得以减小，仅东岸相对位移略有增大，增幅为5.2%；主桥各墩抗震需求趋于均匀，最大剪力/最小剪力比仅为2.19，5#固定墩的抗弯和抗剪需求大幅降低，降幅分别为59.6%、52.2%。