考虑复杂场景的常导高速磁浮辅助停车区优化布置

楚彭子，虞 翊，董丹阳，赵华华，林 辉

（1.同济大学道路与交通工程教育部重点实验室，上海 201804；2.同济大学磁浮交通工程技术研究中心，上海 201804）

凭借噪声小、能耗低、爬坡能力强、选线灵活等优点，磁浮交通受到越来越多的关注。磁浮交通速度范围广泛，涉及中低速域、中速域、高速域、超高速域和宇航域［1］。按照悬浮方式，磁浮交通可划分为4类，即电磁悬浮、电动悬浮、高温超导悬浮与电磁-永磁混合悬浮。由于制式差异，磁浮交通的安全防护与轮轨交通存在差异。作为电磁悬浮型磁浮交通典型代表之一，常导高速磁浮列车在运行时不仅考虑区间限速，还考虑二维速度防护曲线，并采用“停车点步进”运行模式［2-5］，以此来最大限度地保证列车随时能停在设置有供电轨与疏散通道的辅助停车区（auxiliary stopping area，ASA）。作为保障常导高速磁浮列车运行安全的必要组成，辅助停车区（简称为停车区）的布置值得商榷。

根据上海磁浮示范线建设经验，可根据坡度和车长确定常导高速磁浮停车区长度，按照速度等级和坡度情况来划定停车区参考间距［2，6］。类似地，卞建光［6］以列车悬浮距离为基础，给出了不同速度段下的停车区参考间距。针对中高速磁浮停车区，Lai等［7］将停车区的最小长度与停车区的总长设置为约束条件，从安全速度域面积、安全制动曲线和安全悬浮曲线的交点与区间限速曲线拐点之间的欧式距离两方面来优化停车区。以数量最小化为目标，虞翊等［2］将列车运行的连续步进作为约束条件，提出一种从终点站向起点站依次递推的基于防护速度的高速磁浮停车区布置方法。

磁浮交通系统的诸多要素相互耦合，一旦停车区布置完成，可供列车运行曲线调整的安全速度域就被限定，区间追踪间隔时间也将受影响［2，8-10］。针对中低速磁浮列车运行曲线，柴晓凤等［8］将停车区视为约束条件，采用先分析列车运行工况转换点再开展多区间优化的方式来获取节能速度曲线。赖晴鹰等［9］以列车能耗最低为目标，采用变间距动态规划方式来优化中高速磁浮列车运行曲线。Lai等［4］进一步基于动态规划与混合线性整数规划研究了中速磁浮列车节能速度曲线。考虑到车载电池状态，Yang等［10］分析了应急情形下保证磁浮列车能够停在停车区的运行控制策略。

随着磁浮交通运营速度、车辆技术、运控技术以及线路条件的多样化，基于参考间距的布置方式通用性有限，难以获取可靠又经济的停车区布置方案。例如，我国时速600公里级常导高速磁浮系统已经在调试之中，其速度已超过当前参考范围［2，6］。同时，Lai等［7］所述方法未充分考虑停车区布置原则［6］。虞翊等［2］考虑了列车运行曲线、防护速度曲线以及列车运行的连续步进需求，但未能兼顾停车区布置的其他原则。作为一项系统工程，停车区的布置应该考虑所需的目标速度曲线和安全速度域。本文针对以往停车区布置方法的不足，结合常导高速磁浮列车运行特点与停车区布置原则，综合考虑停车区布置中可能遇到的陡坡、道岔、桥梁等复杂场景，建立面向多目标速度曲线且兼顾运行效率的停车区布置多目标优化模型，并针对停车区“低速度区域密集，高速度区域稀疏”的一般特征，设计与改进求解该模型的算法。

1 模型准备

1.1 列车运行与辅助停车区

根据磁浮系统供电特性［2，10］，为了避免列车停在停车区以外区域，造成无法悬浮与疏散困难，对其运行设置了二维速度防护曲线和停车点步进运行模式［2-5］。二维速度防护曲线涉及最大速度曲线和最小速度曲线，而停车点是指车站与停车区。最大速度曲线要求列车能够通过制动停在目标停车点，最小速度曲线要求列车能够惰行至目标停车点。两曲线能够最大限度防止列车速度进入危险速度域［2，4］。借助于二维速度防护曲线，列车采用停车点步进控制方式运行。具体地，列车以当前停车点为目标运行时，以最大速度曲线、最小速度曲线以及区间限速曲线为安全防护要求。仅当列车速度越过下一个停车点的最小速度曲线，且未超过当前停车点最大速度曲线时，执行步进，进而以下一个停车点为目标运行。依此类推，通过连续地步进，最终到达实际终点［2］。同时，磁浮列车的牵引动力源自轨道，涉及一系列牵引分区（简称为分区），每个分区内仅能引导一辆列车正常运行［11］。基于此，类似于轮轨交通闭塞区间的运行区间也依据分区划分［12］。由于磁浮列车依据停车点步进模式运行，且每个分区内只能引导一辆列车，因而列车区间追踪间隔受到分区长度和停车区位置的影响。

具体到停车区，它是设置在磁浮线路安全区域上，配备有供电轨与疏散通道的轨道区段。停车区两端在运控系统中被定义为可达点与危险点。可达点是在关闭牵引系统后，列车依靠当前惯性至少能到达的位置点，是停车区的首端。危险点是列车停车时不能超出的位置点，是停车区的末端。类似地，对车站的两端也可定义可达点与危险点。若将列车视为质点，可达点与危险点的位置可分别作为安全悬浮曲线与安全制动曲线的落脚点。若考虑车长，可将安全悬浮曲线与安全制动曲线的落脚点向中间偏移半个车长。根据停车区性质、列车运行安全影响因素及上海磁浮示范线建设经验，停车区的布置应考虑复杂场景，涉及的原则有［6］：①停车区应布置在适合疏散和安全停留的区域。道岔、陡坡、桥梁、坡度变化点、分区边界以及恶劣地段等为不宜布置停车区的区段（即需求限制区段），在大坡道的坡底与坡顶附近需考虑停车区；②停车区的布置应保证列车正常运行的速度曲线与牵引系统的设计运行曲线一致；③停车区的布置应满足运输组织对列车作业和追踪运行的要求；④站间区间内每个分区均应布置停车区，但不能横跨分区；⑤在满足列车运行安全与运营需求的前提下，考虑布置方案的经济性。

1.2 速度防护曲线的计算

最大速度曲线为列车触及安全制动曲线提供防护，最小速度曲线与安全悬浮曲线之间同样存在安全裕量。安全制动曲线可根据列车运行动力学计算［2，13］，涉及空气阻力、导向轨引发的磁化涡流阻力、涡流制动力、滑撬与轨道的摩擦力、直线电机引起的悬浮阻力和坡道附加阻力。安全制动曲线的计算需要考虑不利条件下的受力特性，包括列车满载、遭遇顺风作用、涡流制动系统部分故障、轨道面与列车滑撬摩擦系数变小［6，13］。根据安全制动曲线，进一步考虑牵引切断命令发出至涡流制动启动的系统延时、测速误差与定位误差以及系统延时内列车加速度可获取最大速度曲线［13］。安全悬浮曲线的计算也需要考虑不利条件，包括列车空载、遭遇逆风、轨道面与列车滑撬摩擦系数变大［2，6］。类似地，进一步考虑牵引切断命令发出至牵引切断完成的系统延时、测速误差、定位误差和系统延时内列车减速度可获取最小速度曲线［13］。本文计算空气阻力Fair、导向轨引发的磁化涡流阻力Fmag、涡流制动力Fedd、滑撬与轨道的摩擦力Fski、直线电机引起的悬浮阻力Fmot和坡道附加阻力Fgra时，参考的公式为［2-3，11，13］：

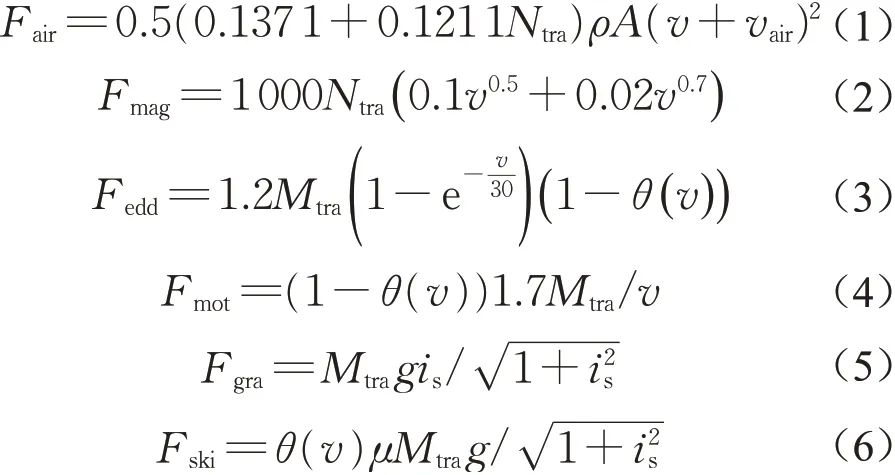
式中：v为列车速度，m·s-1；vair为风速，m·s-1；Ntra为列车编组数；ρ空气密度，通常取1.225 kg·m-3；A为车辆横断面面积，m2；Mtra为列车质量，kg；θ(v)为取0或1的分段函数，当速度大于10 km·h-1时，取0，否则取1；is为轨道坡度，%；g为重力加速度，常取9.8 m·s-2；μ为摩擦系数。

1.3 辅助停车区多目标优化模型

1.3.1 问题描述与假设

已知拟采用的多条目标速度曲线与线路条件，依据停车区的布置原则开展停车区的优化布置，实现资源的有效利用。同时，鉴于停车区对列车区间追踪间隔的影响，若能在节省资源的同时考虑区间追踪间隔，则可以实现资源节省与效率保障的兼顾。基于此，可将问题描述为：已知目标速度曲线与线路条件，在列车安全运行前提下，如何布置停车区，实现停车区总数量尽可能少，区间追踪间隔也尽可能小。作为优化的前提，需要考虑停车区布置场景、列车连续步进需求以及资源的有限性，涉及的假设条件有：①目标速度曲线是已知的，且列车运行时对目标速度曲线的追溯性良好；②停车区的长度分为两种。结合上海磁浮示范线布置经验，长度分为坡度为0时的长度和坡度大于0但不多于0.5%时的长度；③线路上有足够多的候选停车区供优化决策；④线路规划适当，不存在即使在需求限制区段的两端布置停车区也不足以支持列车正常步进的情况；⑤列车蓄电池的电量能保证列车运行至当前停车点。

1.3.2 符号定义

集合方面，S：车站集合，包括起点站ss和终点站st；I：候选停车区集合，下标为i。每个候选停车区包括6个属性：可达点位置RPi、危险点位置HPi、长度ALi、最大坡度SAi、是否位于变坡点、桥梁或道岔SCAi（位于相应位置时取1，否则取0）、跨越分区情况SSAi（横跨分区时取1，否则取0）；K：分区集合，下标为k。每个分区包括3个属性：分区k的范围DSk，长度DLk，以及是否有停车区位于该分区DSAk（有取1，否则取0），且第一个和最后一个分区均为车站；L：优先考虑布置停车区的轨道区段集合，即需求优先区段集合，下标为l。每个需求优先区段包括2个属性：区段的范围RSl，以及是否有停车区位于该区段RSAl（有取1，否则取0）；P：目标速度曲线集合，下标为p。

参数方面，Lmax：停车区总长度的最大值；Ndec：分区的数量；Nreq：需求优先区段的数量；STp，j，j+：目标速度曲线p与停车点j+最小速度曲线的交点和该速度曲线与停车点j最大速度曲线的交点之间的时间间隔，列车需要在该时间间隔内完成步进；STmin：步进冗余时间，是为列车停车点步进过程设置的考虑了冗余量的间隔时间［2］；VL：列车的长度；RLp，k：当列车驶向分区k时，由区间追踪间隔附加时间tr和目标速度曲线p所产生的附加距离；BLp，k：列车依据目标速度曲线p驶向分区k时考虑的安全制动距离；PD：前方分区有列车时，当前目标停车区应距离前方分区边界的作为防护要求的最小距离。

变量方面，ILp，k：列车依据目标速度曲线p驶向分区k时的追踪间隔距离；Vˉp，k：列车依据目标速度曲线p运行时，在追踪间隔距离ILp，k中的平均速度；ITTp，k：列车依据目标速度曲线p驶向分区k时的追踪间隔时间；SLk：满足防护要求且距离分区k最近的停车区末端与分区k边界之间的距离；xi：0-1决策变量，选择候选停车区i作为正式停车区时取1，否则取0。

1.3.3 多目标优化模型

第一个目标函数是最小化停车区数量，可由决策变量累加得到，即：

第二个目标函数是最小化区间追踪间隔时间。如图1所示，只有当列车A出清分区k时，列车B才能以分区k中的停车区为目标停车点进行步进。否则，列车B只能以分区k之前的停车区为目标停车点，且该停车区末端距离分区边界的距离应大于防护距离［12］。

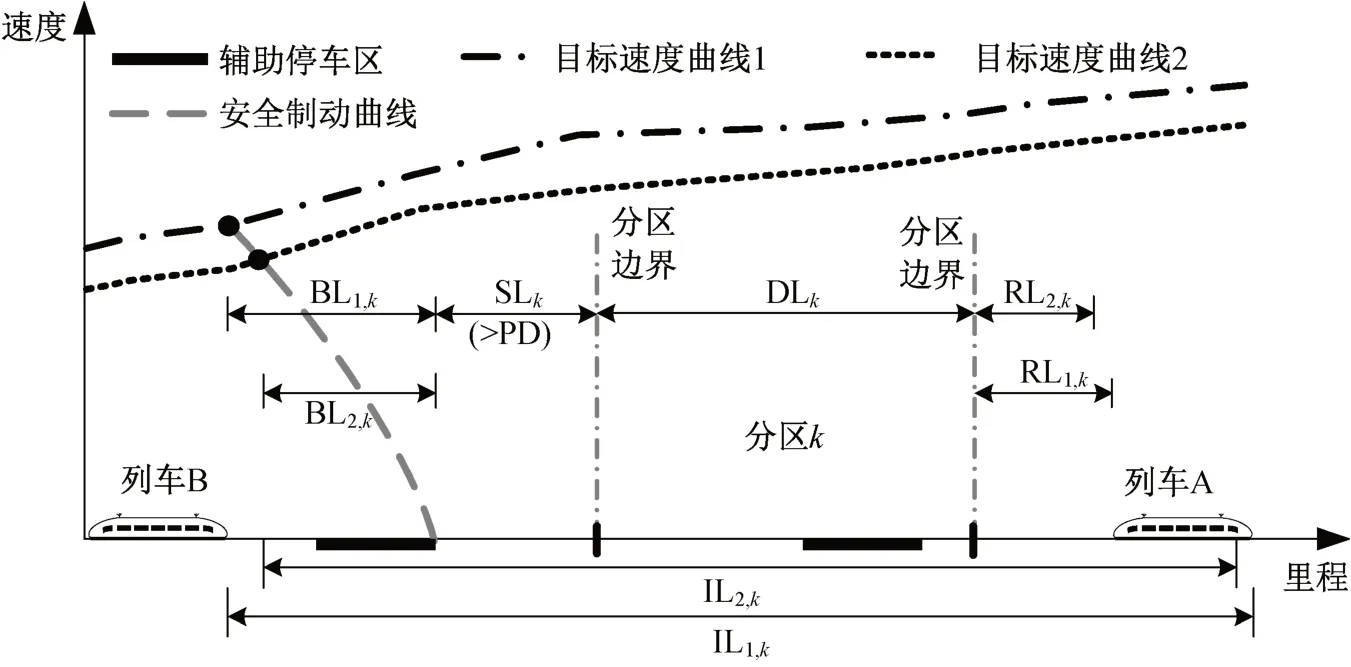
图1 列车区间追踪示意Fig.1 Form of train section tracking

根据目标速度曲线、安全制动曲线、分区长度、停车区危险点与分区边界的距离以及附加距离，列车区间追踪间隔距离可表示为

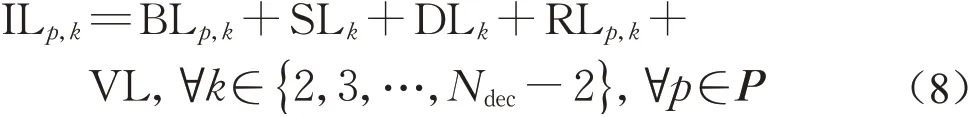
相应的列车区间追踪间隔时间表示为

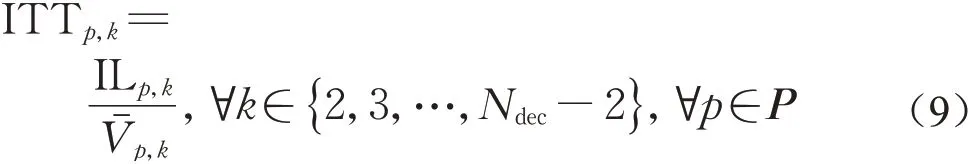
此时，若仅考虑一条目标速度曲线，则区间追踪间隔时间最小可表示为min(max(ITT2，ITT3，…，ITTNdec-2))。当考虑多条目标速度曲线时，可通过引入权重系数（w p，∀p∈P）将区间追踪间隔时间加权平均。此时，有目标函数：

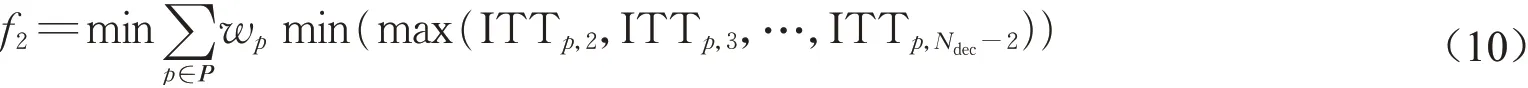
结合停车区布置原则与布置场景，设置了以下约束：

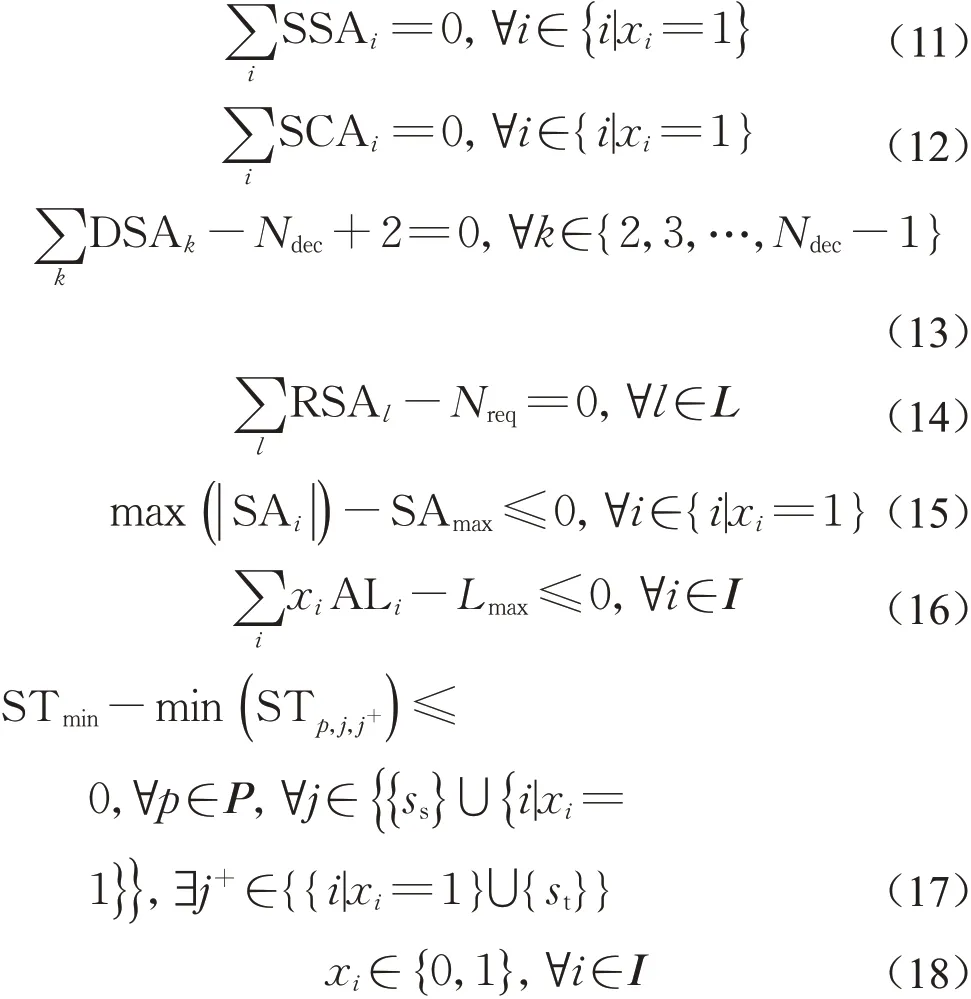
其中：约束（11）表示停车区不能横跨分区；约束（12）要求停车区不能位于变坡点、桥梁或道岔；约束（13）表示站间区间中每个分区均有停车区；约束（14）要求需求优先区段上有停车区；约束（15）代表停车区的坡度不能超过一定范围；约束（16）限制了停车区总长度；约束（17）要求停车区布置方案为列车连续步进提供的时间间隔均不小于步进冗余时间；约束（18）要求决策变量为0-1变量。此外，对于停车区长度，可参考上海磁浮示范线的经验公式（式（19））计算，该公式考虑了轨面结霜的情形。

2 模型求解

针对上述非线性优化模型，本文借助了几乎能求解任何多目标优化问题的带精英策略的快速非支配排序遗传算法（fast and elitist non-dominated sorting generic algorithm，NSGA-II）［14］，并提出了一种符合停车区布置特征的种群初始化策略，讨论了算法求解过程与算法性能指标。

2.1 求解步骤

与传统遗传算法类似，NSGA-II同样基于群体进化思想对解逐步优化。群体中的每一个个体对应着一个解，个体的优劣程度根据目标函数值、约束违反（constraint violation，CV）值（存在约束条件时）、非支配排序（rank）和拥挤距离（crowding distance，CD）共同确定［14］，所得的最优解为Pareto（帕累托）最优解集。图2显示了基于NSGA-II的模型求解过程。该过程涉及两个模块，即仿真模块和求解模块。仿真模块用于模拟列车的运行，判断停车区布置方案的可行性。结合仿真模块输出信息，求解模块可更新与优化停车区布置方案。实施步骤可简单概述如下：

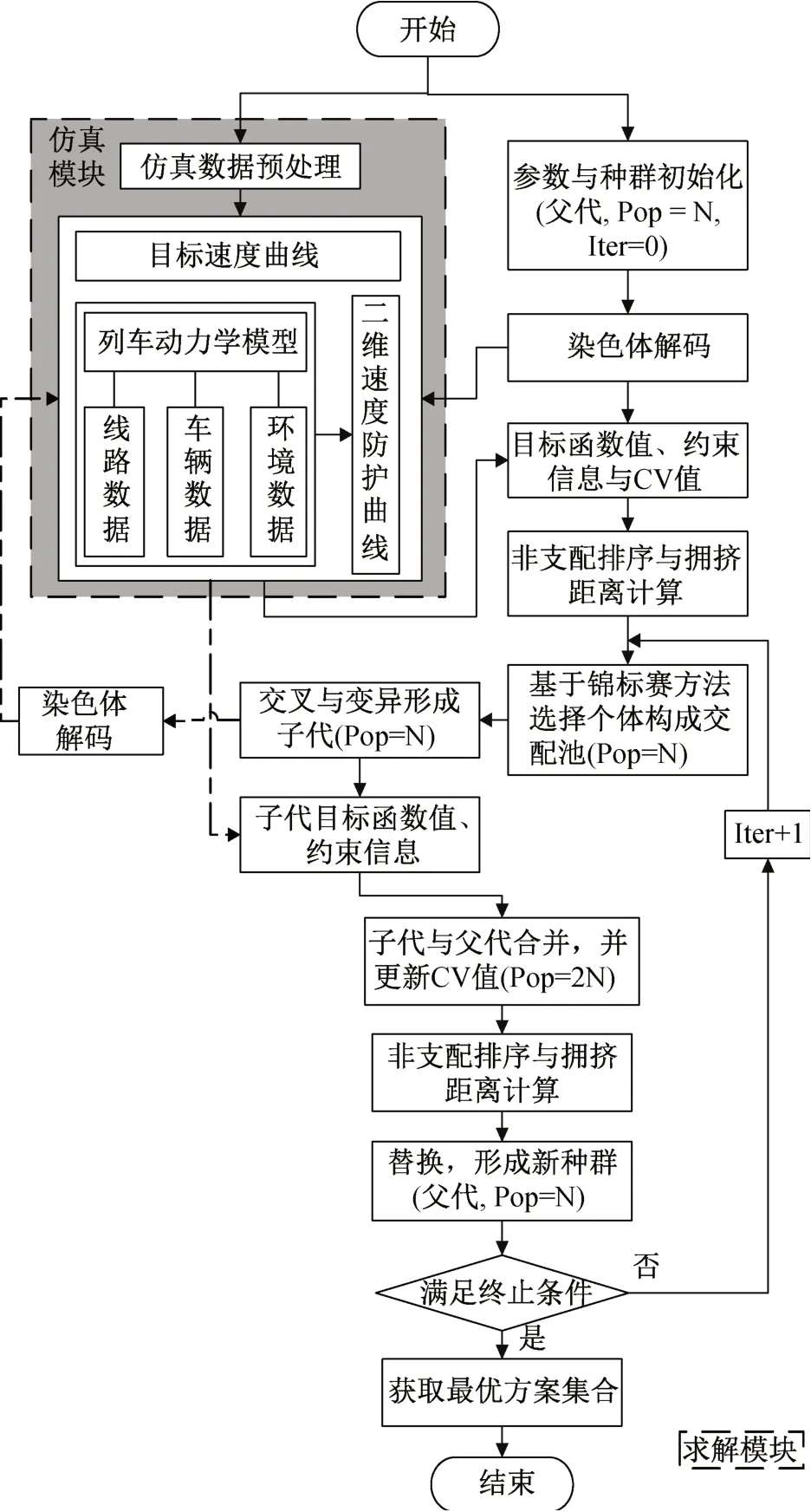
图2 停车区优化过程Fig.2 Optimization process of ASAs

步骤1：仿真模块初始化。初始化仿真模块中的信息，涉及线路数据、车辆数据、环境数据、运控参数与目标速度曲线等。

步骤2：求解模块初始化。初始化求解模块中的参数，包括交叉概率、变异概率、迭代次数（Iter）、种群数量（Pop）等参数，并初始化种群。

步骤3：方案评估。对当前种群中的个体信息进行解码，输入到仿真模块中，进而可以根据目标函数值与约束违反情况获取个体的优劣信息，得到个体的非支配排序与拥挤距离。

步骤4：方案更新。基于个体的非支配排序与拥挤距离，执行选择、交叉、变异、替换等遗传操作。

步骤5：终止判断。若达到预设的终止条件（如迭代次数），输出当前种群中的Pareto最优解集，并作进一步筛选。否则，返回步骤3。

2.2 算法设计

2.2.1 染色体与种群初始化策略

NSGA-II算法中，个体以向量形式进行储存，每个个体代表一个解。由于优化模型中决策变量为0-1变量，本文采用二进制对个体进行编码（图3），该方式也简化了解码步骤。同时，将两个目标函数值、约束违反（CV）值、非支配排序（rank）与拥挤距离（CD）存放于染色体尾部用于遗传操作。

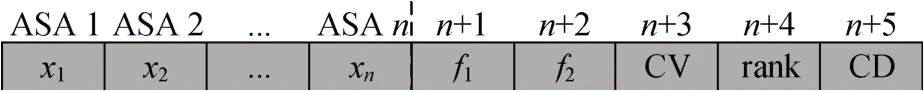
图3 染色体编码Fig.3 Coding form of chromosome

按照一定的分布函数随机生成种群是遗传算法常用方式，如均匀分布。停车区具有“低速区密集、高速区稀疏”的一般特征。对此，提出了一种基于该特征的种群初始化策略（即本文策略）。该方法结合列车运行方向，借助由多条目标速度曲线组合而成的基准速度曲线［2］来确定不同分区中候选停车区被选择的概率，如式（20）和（21）所示。

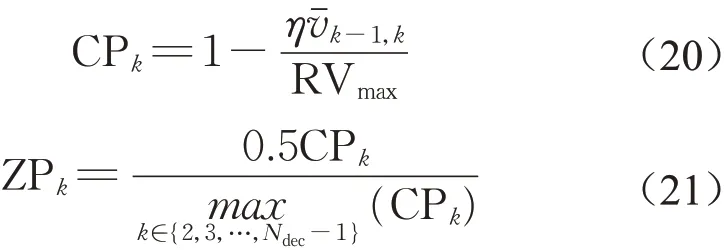
其中：CPk为初始概率；vˉk-1，k为候选停车区所在分区前半部分与前一个分区后半部分基准速度曲线的速度平均值（如果前一个分区是车站，仅考虑当前分区前半部分平均速度）；RVmax为基准速度曲线的最大速度；η为折减系数；ZPk为将CPk归一化后的最终概率；设置折减系数的目的在于增加基准速度曲线的波动性。归一化的目的是使每个候选停车区被选择的概率均不高于均匀分布下的概率，即0.5。

2.2.2 支配关系与拥挤距离

寻找一组非支配解集或Pareto最优解集是多目标优化问题的求解目标。考虑约束条件和不考虑约束条件的支配关系存在差异。以本文优化模型为例，对于解集C中的两个解c1与c2，若不考虑约束条件，如果c1的目标函数值均小于c2，那么c1支配c2，c1为非支配解。如果c1对应的一个目标函数值小于c2，另一个目标函数值相同，那么c1弱支配c2，c1仍为非支配解。若考虑约束条件，除了目标函数值，还需要判断解的可行性，即CV值的大小。此时，c1支配c2的情况分为三种：第一种是c1是可行解，而c2不是可行解；第二种是c1和c2都不是可行解，但CV(c1)小于CV(c2)；最后一种是c1和c2都是可行解，但c1能够在目标函数值上支配c2。对于任意解c，本文采用式（22）计算CV值：

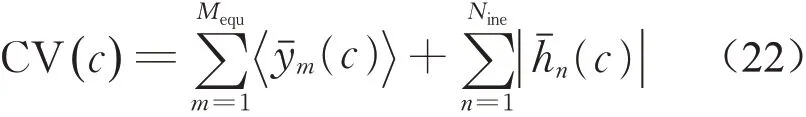
其中：Mequ和Nine分别为优化模型中等式约束和不等式约束的数量；ym(c)为等式约束m左侧项的取值；当ym(c)小于0时，ym(c)取0，否则取ym(c)的绝对值；yˉm(c)是ym(c)归一化后的值；hn(c)为不等式约束n左侧项的取值，|hˉn(c)|是|hn(c)|归一化后的值；本文采用对ym(c)和|hn(c)|除以种群中相应约束项最大值的方式进行归一化。

支配关系通过非支配排序（rank）表示Pareto等级，用于判断解的质量。解的集合中非支配解的等级为1，剩余解中的非支配解等级为2，依次类推［14-15］。拥挤距离的引入则是为了保持解的多样性，是评判个体与相邻个体间远近程度的指标。同Pareto等级的解中，拥挤距离较大的解更容易被选出执行遗传操作。

2.2.3 遗传操作算子

遗传操作算子主要包括选择、交叉、变异与替换。二元锦标赛选择法是常用的选择算法，也是本文采用的方法。该方法随机挑选两个个体，优先选择非支配排序小的个体进入交配池。若个体排序一致，则选择拥挤距离大的个体。若等级与距离相等，则随机选择其中的一个。同时，替换操作也遵循该原则。交叉与变异的目的是为了生成新个体。由于候选停车区数量多，染色体编码长，本文采用一种局部的交叉与变异方式。该算子针对染色体随机选取交叉与变异的起点和终点，并在选定编码区间内开展两个染色体相同位置编码的随机交换（交叉）与单个染色体编码的随机突变（变异）。

2.3 性能评价

从计算效率和解的质量两方面评价算法性能。计算效率可根据算法运行时间进行度量。对于解的质量，平均理想距离（mean ideal distance，MID）是针对多目标优化算法的可靠度量指标。该指标表征了一组满足约束条件的Pareto最优解集Cpar与理想点（即原点（0，0））的接近程度，如式（23）所示［15］。

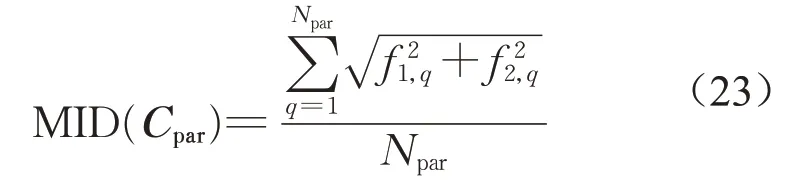
其中：Npar为Pareto解集大小；f1，q和f2，q分别表示第q个解的第1和第2个目标函数值。

3 算例分析

3.1 算例描述

仿真线路全长98 900 m，包括7个分区，线路坡度与分区划分情况如图4所示。其中，起点站加速区末端位置为1 500 m，终点站的始端位置为97 400 m。针对疏散需求，设置有7个需求优先区段，分别为［9 855，11 371］、［14 403，19 038］、［28 571，30 734］、［52 581，55 992］、［68 755，71 536］、［83 751，86 841］与［96 275，96 893］。参考上海磁浮示范线情况，设置采样时间为0.1 s，取列车为5节编组，车长为128.5 m，列车最大、最小重量分别为342 500和256 700 kg，横截面尺寸为3.7 m×4.16 m。

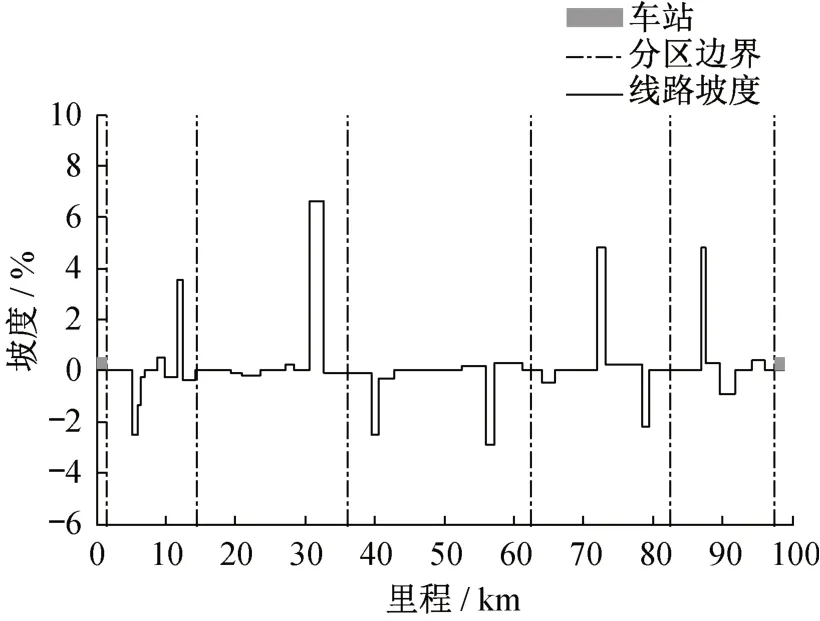
图4 线路坡度与分区划分Fig.4 Line gradient and decentralization division

列车运行方面，考虑了两条目标速度曲线，最大速度分别为450和300 km·h-1，区间追踪间隔的权重分别设置为0.7和0.3，并取分区防护距离为500 m，区间追踪间隔的附加时间为2 s。同时，取步进冗余时间为3 s，牵引切断命令发出至牵引切断完成的延时为1 s，牵引切断完成至涡流制动启动的延时为0.7 s。对于不利条件，取定位测速系统的定位误差为1 m，测速误差为0.2 m·s-1，涡流制动损失系数为0.9，遭遇的不利顺风、逆风风速均为16 m·s-1，摩擦系数最大、最小值分别为0.25和0.1，最大、最小速度曲线计算时的速度变化率分别为0.8和0.5 m·s-2。

为尽可能地得到最优布置方案，根据坡度是否为0，将取整后的停车区长度（309和379 m）从起点站依次不重叠排列，进而把95 900 m的站间区间划分为279个候选停车区，并令正式停车区总长度不多于10 000 m。对于本文种群初始化策略，取折减系数为0.75，得到分区2～6中候选停车区的选择概率分别为0.500、0.367、0.194、0.194和0.195。若采用均匀分布，这些概率均为0.5。算法参数方面，取交叉概率与变异概率分别为0.8和0.2。算例仿真过程借助于MATLAB软件，并依托具有16G内存、i7处理器、64位Windows10系统的笔记本电脑运行。为降低仿真模块时间消耗，预先存储了每个候选停车区最大、最小速度曲线与目标速度曲线的交点。此外，作为对比，以相同的数据分析了文献［2］中的布置方法。

3.2 结果与分析

针对两种种群初始化策略，将群体数量设置为200，迭代次数设置为100，分别进行了仿真优化。根据输出的Pareto最优解集，随机展示了两组布置方案，如图5和图6所示。结合图4和1.2节可知，坡度对最大速度曲线和最小速度曲线的加速度有较大影响。上坡坡道能增大速度变化率，进而压缩停车区之间的间隔。同理，下坡坡道则有助于增大停车区之间的间隔。

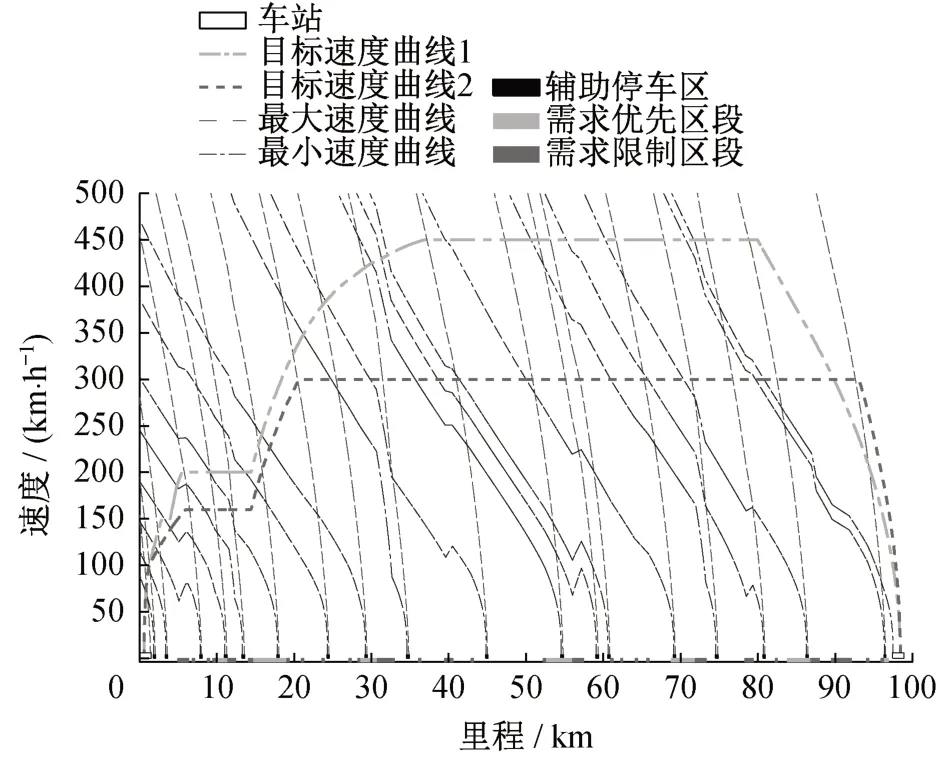
图5 基于均匀分布的结果Fig.5 Result based on uniform distribution

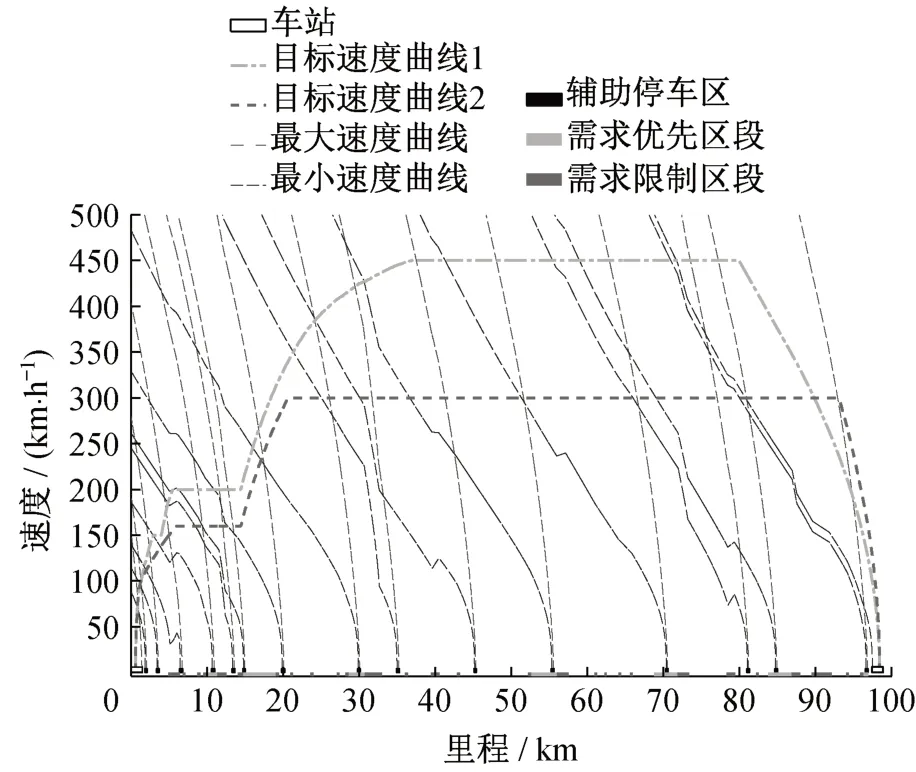
图6 基于本文策略的结果Fig.6 Result based on proposed strategy

图5 和图6中停车区数量分别为18和15，加权后的区间追踪间隔分别为300.321 s和299.461 s，即图6方案在停车区数量与区间追踪间隔上更理想。同时，两者所在的Pareto最优解集CV值均为0，MID分别为300.860和299.836，运行时间分别为214.242 s和由此可知，无论采用本文策略，还是基于均匀分布的种群初始化策略，使用局部交叉与变异算子都是可行的，且本文种群初始化策略似乎有助于提高算法性能。进一步地，针对均匀分布和本文策略对NSGA-II算法求解性能的影响，使用相同的迭代次数（100次）与种群数量（200）分别运行30次。结果显示，基于均匀分布和本文策略所得平均理想距离平均值分别为304.272和300.529。相应地，运行时间平均值分别为228.365和136.666 s。由此可见，无论是最优解集的平均理想距离还是运行时间，基于本文策略的表现均优于基于均匀分布的种群初始化策略。因而，引入停车区布置特征的种群初始化策略对于使用NSGAII算法求解本文模型是有益的。此外，本文基于文献［2］中方法得到了含有11个停车区的方案，但对应的加权求和后区间追踪间隔为347.872 s，大于图5和图6中的结果。同时，由于该方案未考虑复杂场景，部分需求限制区段中存在停车区，也有部分需求优先区段中未布置停车区。因此，本文方法较文献［2］更能应对停车区布置中的复杂场景。

4 结语

针对现有高速磁浮停车区布置方法难以应对复杂场景，在考虑运营效率与多目标速度曲线需求的同时，建立了停车区多目标优化模型。基于所设计的带精英策略的快速非支配排序遗传算法，讨论了优化模型求解过程。算例仿真结果表明，本文模型可用于布置方案的求解，提出的种群初始化策略有助于改善算法性能，对染色体执行局部交叉与变异具有良好的适用性，实践中可使用所述种群初始化策略和遗传算子。本文模型与算法可为单向运行常导高速磁浮停车区的布置提供参考，为相关辅助设计软件的开发奠定基础。后续研究可进一步着眼于考虑双向运行的磁浮线路停车区优化布置。

作者贡献说明：

楚彭子：研究构思、文章撰写、实施研究。

虞翊：研究构思、研究指导、研究经费、文章审阅与修改。

董丹阳：文章撰写、软件仿真。

赵华华：研究指导。

林辉：研究指导。