层状地基中考虑桩端应力泡形扩散的单桩沉降计算方法
王立兴,吴文兵,,杨晓燕,张云鹏,王奎华
(1.中国地质大学 工程学院,武汉 430074;2.浙江大学 滨海和城市岩土工程研究中心,杭州 310058)
桩基沉降计算是桩基工程设计中非常重要的部分。学者们对桩基沉降进行了广泛而深入的研究,得到了很多有价值的单桩沉降计算方法,如荷载传递法[1-7]、剪切位移法[8-10]、弹性理论法[11-13]、规范法[14]和数值计算法[15-17]等,其中,荷载传递法因可通过不同的桩土相互作用模型来反映桩土共同作用、地基层状特性而被学者广泛运用。总的来说,基于荷载传递法的桩-土相互作用模型主要有理想弹塑性模型[1,4-6]、双折线硬化模型[3,18]、三折线模型[19]及双曲线模型[7],通过选取不同的桩-土相互作用模型,可以较准确地得到不同土性中单桩的沉降,具有较好的工程适用性。
上述研究采用荷载传递法计算桩基沉降时,均将桩端土对桩的支撑作用简化为弹簧模型,弹簧参数可结合桩端土硬化特性、非线性特性等根据实测的桩端反力-位移曲线反演确定。然而,这种弹簧支撑模型存在一些不足:无法考虑桩端土体的层状特性;无法建立桩端土层物理力学性质与弹簧参数之间的相互关系;且无法反映持力层内及以下土体性质的变化对单桩沉降的影响[20]。为此,Wu等[20-21]提出了虚土桩模型,并用于桩基纵向和扭转动力特性分析。随后,王奎华等[22]率先将虚土桩模型应用于层状地基中的单桩沉降计算分析,并提出采用锥型虚土桩模型来考虑桩端应力扩散效应对单桩沉降的影响[23],辛冬冬等[24]将虚土桩模型推广到层状地基中的群桩沉降分析。尽管虚土桩模型能很好地考虑桩端层状特性对基桩静动力学特性的影响,且能在一定程度上考虑桩端应力扩散效应,但虚土桩的合理长度及应力扩散影响范围到底多大仍不得而知。
为了更好地分析桩端土性质对单桩沉降的影响,笔者基于Boussinesq解提出了一种应力泡形虚土桩模型来考虑桩端应力扩散效应,并基于荷载传递法对桩侧土采用双折线模型、对桩端土采用应力泡形虚土桩模型,考虑桩端土中实际附加应力的分布情况,推导得到了成层地基中的单桩桩顶沉降计算公式。
1 数学模型及假设条件
1.1 应力泡形虚土桩模型的建立
根据Boussinesq解可知,桩端土体中附加应力大致的分布规律为:在径向上随着径向半径的增加逐渐减小,在竖向上随着深度的增加也逐渐减小,在整体空间中呈椭球型泡状分布,即应力泡。假设桩端对土体的作用力为均布荷载形式,根据Boussinesq解可以求出桩端土中应力分布形式的解析式,然后建立应力泡形虚土桩模型。建立如图1所示的轴对称坐标系,基于Boussinesq解,通过积分可以求得圆形均布荷载作用下地基土体中任意一点的竖向应力分布[25]。

图1 桩端附加应力计算模型Fig.1 Calculation model of additional stress at pile
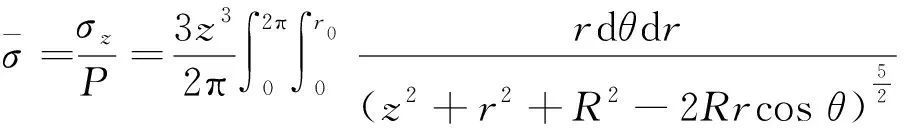
(1)

将式(1)求解得到的相同数值的竖向应力等值线绕z轴旋转一周就形成一系列以z轴为中心的三维应力等值面,将等值面以内的土体看作是受荷主体,即为应力泡形虚土桩的主体部分,如图2所示。

图2 应力泡形虚土桩模型Fig.2 Stress-bubble fictitious soil pile
1.2 桩土相互作用模型的建立
桩周土采用双折线模型,如图3所示,荷载传递函数为

图3 桩周土本构模型Fig.3 Constitutive model of soil around
(2)
式中:u为桩周土的位移;ub为桩周土的弹性极限位移;fs为单位长度桩周侧摩阻力;λ为理想弹塑性模型的弹性抗剪切刚度系数,kN/m2。
桩端土采用应力泡形虚土桩模型,把桩端至基岩之间的应力泡形土体看成“土桩”,即所谓虚土桩,其参数分别取各实际土层参数,而变形按类似于桩的平面假定。根据桩端土层成层性情况及桩端土体性质和受力环境是否变化而把实体桩和虚土桩一共分为n(n>m)段,其中实体桩分成m段,虚土桩分成N(即N=n-m)段,从实体桩顶部向下依次编号为1、2、…、i、…、m、m+1、…、n,各桩段厚度分别为l1、l2、…、li、…、ln,实体桩总长为L1,虚土桩总长为L2,各段桩的埋深分别为z1、z2、…、zi、…、zn。计算时,可以将虚土桩各桩段再细分为很薄的圆柱体进行近似计算,计算精度由单元数N控制,计算中可以直接将桩土体系按照m+N段进行计算。具体的桩体分段与桩土相互作用体系简图如图2所示。由式(1)可求得虚土桩各深度桩段对应的半径Ri,即各段实体桩和虚土桩的半径分别为
(3)
1.3 桩土体系相关假设
1)桩土体系呈线弹性状态,实体桩桩身截面均匀,虚土桩以应力泡的形式存在。
2)桩体与土体之间没有相对滑移,实体桩与虚土桩的各桩段交界面之间为完全连续接触,满足连续性条件。
3)桩单元中任意点的位移只与该点的桩周侧摩阻力有关,虚土桩端部为刚性支撑。
4)地基中同一土层的物理力学性质沿深度方向不变。
5)虚土桩的力学行为与桩体相符合,参数为土体参数。
2 桩顶沉降计算方程建立及求解
根据荷载在桩身的传递机理,桩体的截面轴力及位移随深度的增加,逐渐减小,且随着桩顶荷载的增加,截面轴力及位移逐渐向桩底发展。因此,随着荷载的增加,桩周土由浅入深逐渐进入塑性阶段。根据桩土体系所处状态的不同,分3个阶段分别给出桩顶荷载和沉降的计算公式。需要说明的是,由于桩基受力后通常仅对桩周径向一定范围内的土体产生影响,这里所指的桩周土体即桩基应力影响范围内的土体。
首先推导荷载传递函数基本微分方程,根据桩上任意一个单元体的静力平衡条件,可以得到
(4)
(5)
式中:E为该桩段弹性模量;A为该桩段截面面积;P为该桩段顶部荷载。
对式(5)两端求导,并将式(4)代入,可得荷载传递法的基本微分方程
(6)
2.1 桩周土全部处于弹性阶段
当桩顶荷载较小时,桩周土全部处于弹性阶段,根据式(4)~式(6),此时第i个桩段截面位移u(x)应满足方程
(7)
式中:Pi为第i段桩体顶部荷载;Si为第i段桩体顶部位移;zi为第i段桩体截面到桩顶的距离;Ei为第i段桩体弹性模量;Ai为第i段桩体横截面积;λi为第i段桩体弹性抗剪切刚度系数。
各虚土桩段面积Ai值计算采用式(8)。
(8)
为使解析表达式简洁,定义式(9)。
(9)
求解式(7)可得第i桩段截面位移为
(10)
联立式(7)与式(10)可求得第i段桩的桩顶荷载及位移为

(11)
由式(11)可得第i段桩的桩顶刚度Ki(刚度是指材料或结构在受力时抵抗弹性变形的能力)。
(12)
由假设条件(3)可以得知,虚土桩桩端位移为0,即
u|x=L1+L2=Sn+1=0
(13)
由式(10)和式(11)给出的第i段桩的桩顶荷载及位移并结合边界条件式(13)就可以求得第n段桩的桩顶刚度为
(14)
根据式(12)和式(14)可以递推得到桩体顶部刚度K1,进而根据桩顶荷载P1,就可以求得桩顶沉降值S1。
(15)
式(12)和(14)中所需要的计算参数均可以由实测的土层参数直接或间接计算得到。因此,根据式(11)~式(15)就可以求得桩顶沉降值。
2.2 桩周土部分处于塑性阶段
桩周土部分处于塑性阶段时,桩土的相互作用体系简图如图4所示,塑性桩段的长度为La,由于塑性桩段的长度La与桩顶荷载和桩周土的性质有关,在实际工程应用中应当根据现场试验确定桩周土处于塑性阶段的深度La。

图4 桩周土部分进入塑性阶段模型Fig.4 Model of part of the soil around the pile
对于桩侧土体处于塑性阶段的连续桩段,第i个桩段截面位移u(x)应该满足方程
(16)
式中:ubi表示第i桩段桩周土的极限位移。
求解式(16)可得第i段桩的截面位移方程为
(17)
求得第i段塑性桩的桩顶荷载及位移为
(18)
根据假设,当桩周土部分处于塑性阶段时,可以依据桩周土所处的状态把桩分为两个部分,即塑性段和弹性段,先按照式(11)~式(15)计算弹性桩段的刚度,再按照式(18)计算塑性桩段的刚度,就可以得到单桩桩顶沉降值。
2.3 桩周土全部处于塑性阶段
桩周土全部处于塑性阶段时,如图4所示,即La=L1+L2。可求得第n段桩的桩顶荷载及位移为
(19)
当桩周土全部处于塑性阶段时,结合式(18)和式(19)递推就可以得到单桩桩顶沉降值。
3 计算参数的选取及影响
3.1 弹性极限位移ub
对于弹性极限位移,很多学者都有研究,目前有经验法[26-27]、经验公式法[28]及应变计测试方法[29]。为了在实际工程应用中方便取值,建议采用应变计测试方法进行计算。
(20)
式中:s0为桩顶沉降量;ubi为第i段桩土体系的极限位移;li为第i段桩的长度;εi为静载试验中在桩顶作用承载力设计值时第i个测试面的应变。
通过静载试验,将加载到极限承载力时测试得到的桩顶沉降量和应变值代入式(20),就可以求得桩土弹性极限位移。
3.2 弹性抗剪切刚度系数λ
与弹性极限位移类似,为了在实际工程应用中方便取值,建议弹性抗剪切刚度系数采用应变计测试方法进行计算。
(21)
式中:τui为第i段桩的极限侧摩阻力;τi与ui为静载试验某一级荷载作用下计算得到的第i段桩的侧摩阻力与相对位移。
在双折线模型中,λ为斜线段斜率,知道任一点的侧摩阻力和相对位移就可以计算得到抗剪切刚度系数。
3.3 附加应力值σz
由式(1)可以看出,附加应力值σz是利用应力泡形虚土桩模型分析单桩沉降的一个重要参数,选取不同的附加应力值σz意味着选用了范围大小不同的应力泡形虚土桩模型,如图5所示。桩端土体的沉降对桩顶沉降有较大的贡献,因此,选取范围不同的应力泡形虚土桩模型对桩顶沉降影响很大。

图5 泡形不同的虚土桩模型Fig.5 Virtual soil pile models with different bubble
3.3.1 算例1:桩端土为软弱土 为了考虑桩端应力泡范围不同的影响,取上硬下软双层土作为算例1,实体桩深度范围内为硬黏土,虚土桩范围内为软弱土,土层参数来源于文献[30],如表1所示。

表1 算例1各参数取值[30]Table 1 Values of parameters in study 1
桩身弹性模量Ep=3×104MPa,桩身半径r0=0.5 m,桩顶荷载P取2 000、3 000、4 000 kN,附加应力值σz取0.1P~0.000 01P,虚土桩部分按照0.5 m分层计算,得到桩顶的沉降值如图6所示。

图6 上硬下软土层中应力泡范围对桩顶沉降的影响Fig.6 Influence of stress bubble range on pile top settlement in upper and lower soft soil
如图6所示,在桩侧土为硬土,桩端土为软土的双层地基中,附加应力范围对桩顶沉降的影响不明显,沉降变化不大。整体上,随着附加应力范围的增大(即应力泡形虚土桩范围增大),桩顶沉降随之减小,但减小幅度不大。
3.3.2 算例2:桩端土为硬黏土或砂性土 取上软下硬双层土作为算例2,实体桩深度范围内为软弱土,虚土桩范围内为硬黏土或砂性土,各参数取值如表2所示。

表2 算例2各参数取值[30]Table 2 Values of parameters in study 2
桩身弹性模量Ep=3×104MPa,桩身半径r0=0.5 m,桩顶荷载P取2 000、3 000、4 000 kN,附加应力值σz取0.1P~0.000 01P时,虚土桩部分按照0.5 m分层计算,得到桩顶的沉降值如图7所示。

图7 上软下硬土层中应力泡范围对桩顶沉降的影响Fig.7 Influence of stress bubble range on pile top settlement in upper and lower hard soil

综合上述分析发现,当桩周土性好时,桩以侧阻为主,应力泡形虚土桩范围的大小对桩顶沉降量影响不大;而当桩周土性差时,桩以端承为主,应力泡形虚土桩范围的大小对桩顶沉降量影响明显;且当应力泡的影响深度大于桩端土层厚度时,会有沉降值的突变。实际工程中,应针对不同类型的桩周土及桩端土的性质与桩端土的厚度,选择合适的应力泡范围,当桩端土厚度并非过大时,可以选择应力泡的影响深度等于桩端土厚度时的应力泡作为虚土桩模型的边界进行计算。
4 工程实例分析
王奎华等[23]提出了考虑应力扩散角的桩顶沉降计算模型,并通过计算两根试桩的沉降与实测值对比验证了其实用性。为验证该方法的合理性及实用性,对文献[23]中的T3、T4桩进行拟合,并将拟合结果与原文实测值及其计算值做对比分析,与文献[23]保持一致,采用桩周土处于弹性阶段公式计算。桩周土及桩端土的物理力学性质参数来源于文献[23],如表3所示。

表3 实例地质资料与模型参数[23]Table 3 Geological information of example and parameters of model[23]
T3试桩:桩直径为800 mm,桩长61.8 m;T4试桩:桩直径为1 000 mm,桩长73.8m,桩身弹性模量Ep=3.3×107kPa。采用本文解计算各桩顶沉降量并与文献[23]计算结果及实测值对比,见图8及图9。利用该方法计算时,T3桩与T4桩的虚土桩部分取至第15层粉土底部,根据式(1)计算虚土桩影响深度刚好为第15层粉土底部时的T3试桩附加应力值为0.000 36P,T4试桩附加应力值为0.001 2P,并分别选取此时的应力泡范围作为虚土桩边界进行计算。
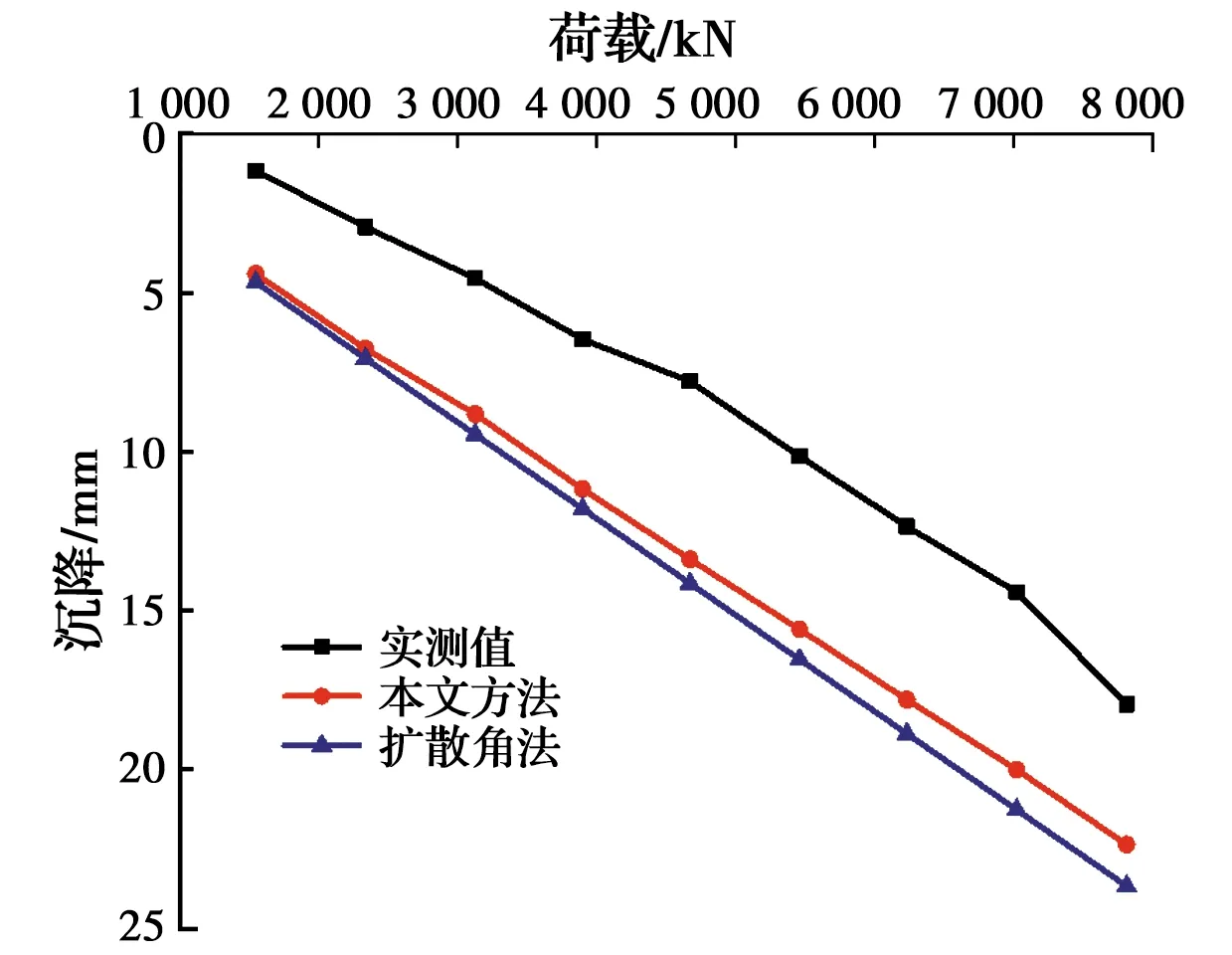
图8 T3桩桩顶沉降计算结果对比Fig.8 Comparison of calculation results of pile top settlement of T3

图9 T4桩桩顶沉降计算结果对比Fig.9 Comparison of calculation results of pile top settlement of T4
与两根试桩的实测值与文献[23]的扩散角法计算值对比可以发现,该方法考虑应力泡形扩散的计算结果与文献[23]考虑应力扩散角的计算结果较为接近,与实测结果具有较好的一致性。与文献[23]的锥形虚土桩模型相比,该模型的最大优势在于能够较严格地给出桩端应力扩散边界,因而具有更广泛的工程应用价值。
5 结论
1)基于虚土桩模型并结合Boussinesq解,提出了考虑桩端应力扩散效应的应力泡形虚土桩模型,并建立了基于该模型单桩沉降计算的解析解。该解能够计算桩侧土体处于弹性及塑性阶段时的桩顶荷载-沉降曲线,参数明确,应用简便,可以用于工程现场单桩沉降量的计算分析,为桩基础设计提供较为准确的沉降值。
2)当桩周土性较好时,桩侧摩阻力发挥主要作用,桩周土承担主要荷载,应力泡范围的大小对桩顶沉降量影响不明显,可取较小范围的应力泡形虚土桩;当桩周土性较差时,桩端阻力发挥主要作用,桩端土承担主要荷载,应力泡范围的大小对桩顶沉降量影响明显,应针对不同类型的桩周土及桩端土的性质与桩端土的厚度,选择合适的应力泡范围。
3)通过分析不同附加应力取值对单桩桩顶沉降量的影响发现,当应力泡的影响深度大于桩端土厚度时,会发生沉降量的突变。因此,在工程应用中,可以选取应力泡的影响深度恰好是桩端土厚度时的应力泡形虚土桩模型进行计算。
4)该方法与锥形虚土桩模型对两根试桩的沉降计算结果与实测结果对比表明,该方法的计算结果与实测结果有较好的一致性。同时,该模型的最大优势在于能够较严格地给出桩端应力扩散边界,因而具有更广泛的工程应用价值。

