玻璃纤维管钢筋混凝土空心柱的轴压徐变性能
张霓,郑晨阳,羡丽娜,王连广
(1. 辽宁工程技术大学 土木工程学院,辽宁 阜新 123000;2. 东北大学 资源与土木工程学院,沈阳 110000)
玻璃纤维管钢筋混凝土柱是将纵向受力钢筋放置于玻璃纤维管内,并在管内灌注混凝土形成的实心柱。玻璃纤维管优良的抗腐蚀性能可以保护内部纵向钢筋和混凝土,同时,混凝土强度因玻璃纤维管的约束作用得到提高。该结构的优异性能受到工程界的广泛关注,由于该结构更能适应当今工程结构承受恶劣环境的需要以及向重载、轻质、大跨及高强发展的要求,因而在地下工程、民用建筑、桥梁和海洋工程中得到越来越广泛地应用[1-3]。随着研究和应用的不断发展,从玻璃纤维管钢筋混凝土实心截面逐渐发展到空心截面[4-6]。空心柱中的混凝土在长期使用过程中受轴压作用产生徐变,玻璃纤维管、纵向受力钢筋和混凝土之间会发生内力重分布现象,与普通钢筋混凝土结构类似,混凝土徐变的不断变化将影响玻璃纤维管钢筋混凝土空心结构的应变状态,而与普通钢筋混凝土结构徐变相比,玻璃纤维管钢筋混凝土空心结构中混凝土的徐变性能因其处于三向受力状态变得更加复杂,因此,准确预测徐变的变化对玻璃纤维管钢筋混凝土空心组合结构有着重要意义。玻璃纤维管钢筋混凝土空心柱的徐变问题随着其广泛应用而变得越来越突出。目前,研究人员对该新型结构的研究主要以玻璃纤维管钢筋混凝土空、实心柱轴心受压、偏心受压和受弯性能以及其实心柱徐变性能为主[7-10],但对于该空心柱徐变性能的研究并不多见[11]。笔者根据玻璃纤维管钢筋混凝土空心组合柱受力特点,对该空心柱受力性能进行分析,建立轴压徐变计算公式,并编制该空心柱轴压下徐变分析程序,计算空心率、作用荷载、混凝土强度及玻璃纤维管壁厚等主要参数对其轴压徐变性能的影响,以供工程实践参考。
1 初始状态受力分析
1.1 弹性阶段的约束力
截面应力由弹性力学的拉梅公式[12]计算。
式中:σφ、σρ分别为环、径向应力;p1、p2分别为圆筒的内、外压力;r、R分别为圆筒内、外径。
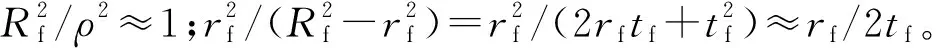
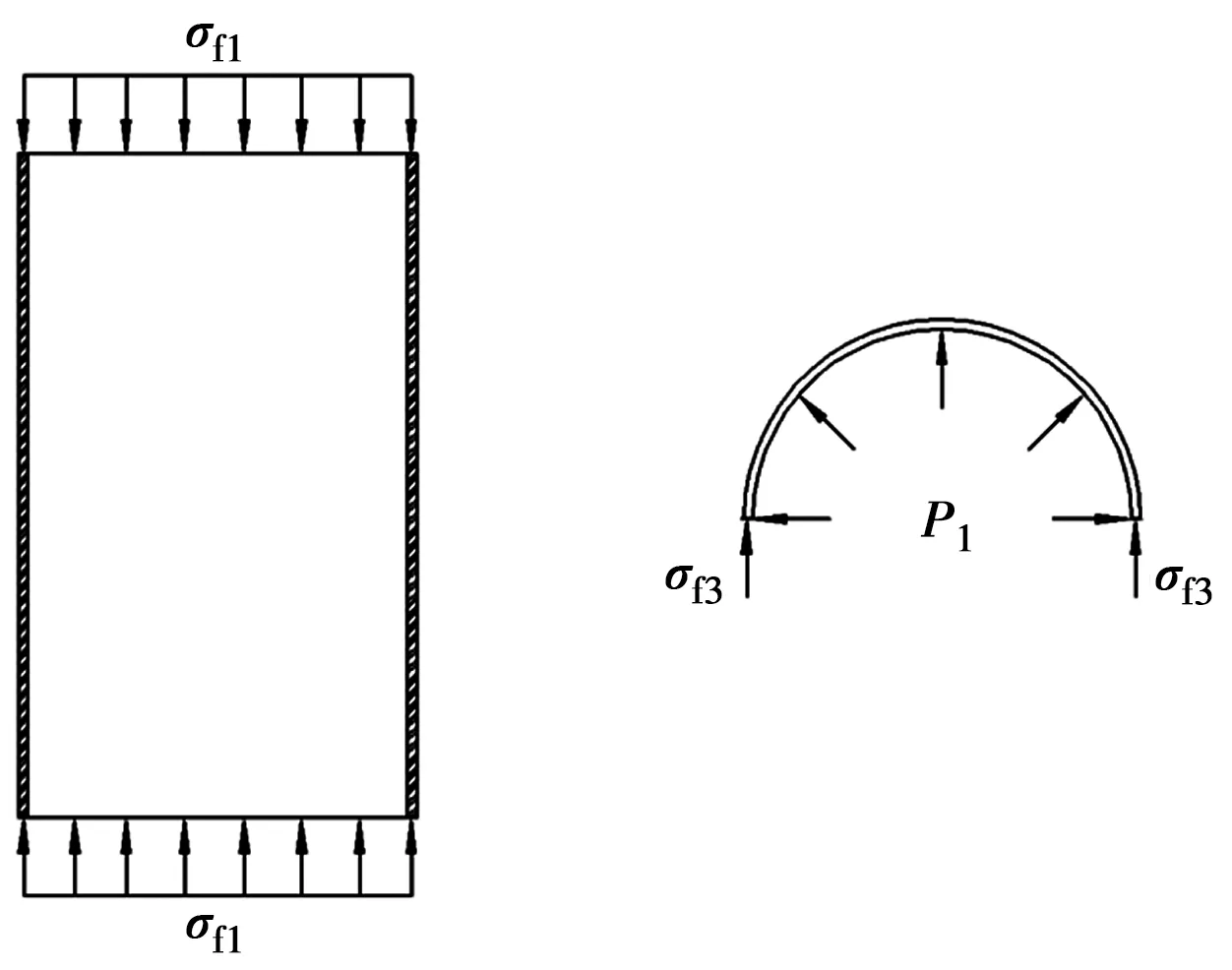
图1 玻璃纤维管受力图Fig.1 The force diagram of GFRP
玻璃纤维管的环、径向应力表示为
式中:σf3、σf1分别为玻璃纤维管的环、纵向应力。
玻璃纤维管环、纵向应变表示为
(1)
式中:Ef3、Ef1分别为玻璃纤维管的环、纵向弹性模量;μf3、μf1分别为玻璃纤维管的环、纵向泊松比。
1.1.2 混凝土受力分析 图2为混凝土受力图。
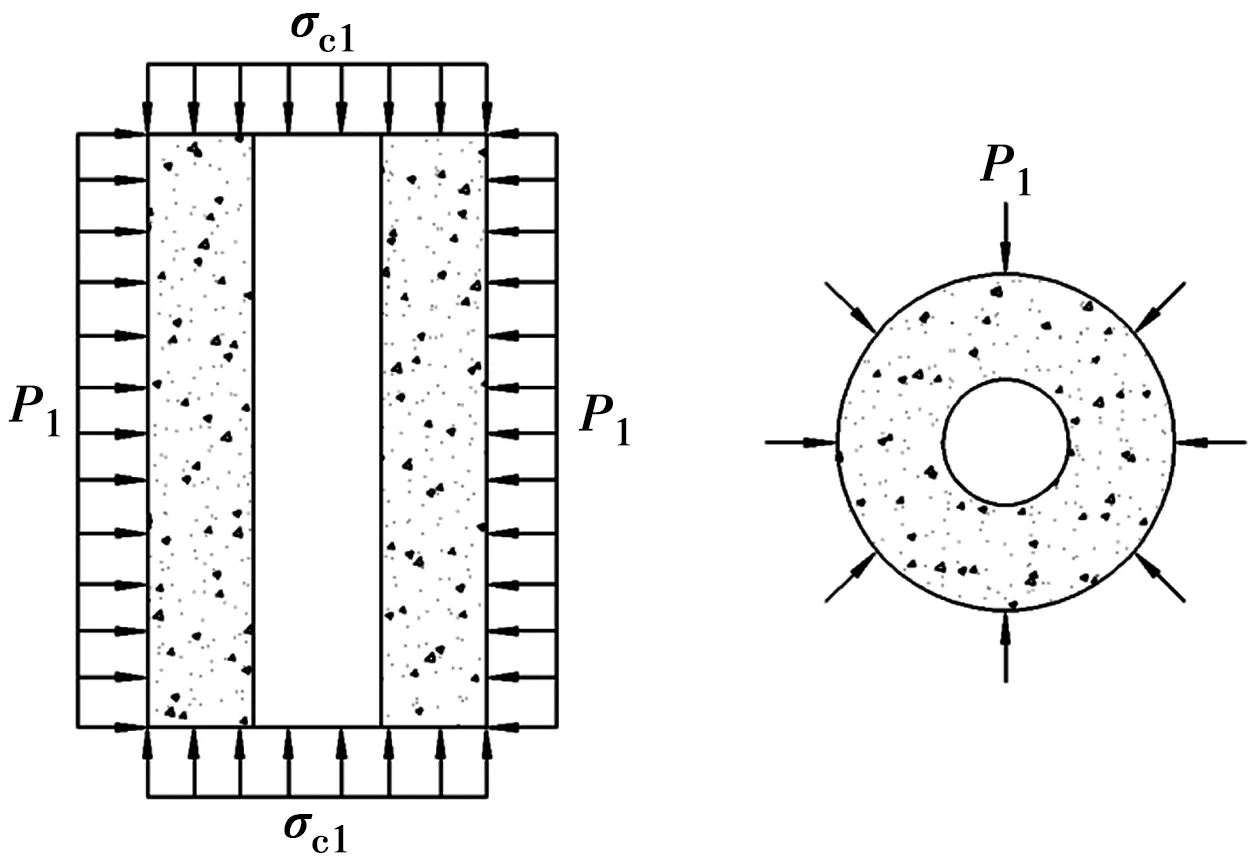
图2 混凝土受力图Fig.2 The force diagram of
混凝土应力状态为等向侧应力状态,即
σc2=σc3=p1
由胡克定律得混凝土应变
(2)
式中:Ec为混凝土弹性模量;σc1为混凝土纵向应力;μc为混凝土泊松比。
μc为随徐变变化而变化的一个变量,因混凝土处于三向受力状态,故该值由文献[13]公式计算。
式中:F=0.16+0.53α;G=1.96-1.94α;α=Af/Ac,Ac、Af分别为混凝土、玻璃纤维管的截面面积;φ为套箍系数,φ=αff/fck;[σ0]为混凝土极限应力。
1.1.3 约束力计算 由纵向变形协调条件可知,混凝土和玻璃纤维管的纵向应变相等,即εc1=εf1。
(3)
同理,混凝土的径向应变和玻璃纤维管的环向应变相等,即εc2=εf3。
整理得
(4)
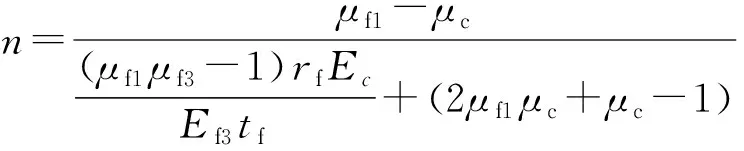
可得p1=nσc1。
1.2 初始应力分析
玻璃纤维管对混凝土具有套箍约束作用,故在进行初始应力分析时,应考虑套箍约束作用的影响,则
N=Ns+Nc+Nf
N=σs1As+σc1Ac+σf1Af
(5)
纵向钢筋与混凝土的纵向应变相等,即εs1=εc1。
由式(3)和式(4)得
整理得
(6)
2 徐变计算公式
混凝土、纵向受力钢筋和玻璃纤维管在轴压下共同受力,但因混凝土和玻璃纤维管不同的泊松比,在空心柱受力过程中,混凝土受到玻璃纤维管的套箍约束作用。空心柱发生徐变时,截面上的应力因混凝土处于卸载状态发生重分布,应力逐渐向玻璃纤维管和纵向受力钢筋转移,导致玻璃纤维管和纵向受力钢筋应力增加。
依据混凝土多轴徐变理论[14],混凝土纵向有效泊松比μcp,1为
纵向徐变度c1为
式中:c为素混凝土徐变度;σu为单轴应力下混凝土的纵向应力。
因空心柱发生徐变时内部混凝土处于不断卸载状态,故空心柱的徐变度c由混凝土徐变继效流动理论[14]计算得到。
c=[1.51(1-e-2.7(t-t0))+3.34(1-e-0.14(t-t0))+
2.17(1-e-1.15(t-t0))+8.85(1-e-0.015(t-t0))]×10-6
混凝土纵向应力σc1与混凝土的纵向应力σu在单轴应力下相等,得σc1=σu。
纵向徐变度c1化为
c1=(1-2μcp,1·n)·c
(7)
在空心柱发生徐变时,空心柱截面上的应力会发生应力重分布,但这种应力重分布对外荷载无影响,故
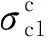
玻璃纤维管增加的弹性应变
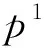
混凝土的徐变
徐变对横向变形的影响
式中:c2为混凝土径向徐变度。
在计算混凝土的侧向徐变度时,由于空心柱中约束力的增量Δp1较小,因此,可将其忽略。
式中:μcp,2为混凝土侧向徐变泊松比。
令σu=p1,有
(8)
玻璃纤维管约束力的增量
(9)
简化得
(10)
其中
则
混凝土在徐变中产生的应力增量
(11)
玻璃纤维管钢筋混凝土空心柱在轴压荷载下的徐变计算公式
(12)
3 设计参数的影响
根据以上公式,编制玻璃纤维管钢筋混凝土空心柱在轴压下的徐变计算分析程序,计算空心率、作用荷载、混凝土强度和玻璃纤维管壁厚等参数对徐变的影响。
3.1 公式验证
为验证徐变分析程序的正确性,将计算得到的徐变应变-时间关系曲线分别与文献[15]的试验试件B3、文献[16]的试件L1-0.3和L2-0.3进行对比,见图3。从图3可以看出,空心柱的徐变在28 d以内(作用初期)增长较快,28 d以后增长速度变得相对缓慢,大约6个月后徐变应变趋于稳定。总体来说,计算结果偏于保守,且与试验结果吻合较好。文献[15]混凝土直径150 mm,混凝土28 d立方体抗压强度51.1 MPa,纵向钢筋为4根直径8 mm的螺纹钢筋,纵向钢筋屈服强度256 MPa,FRP壁厚0.572 mm,极限强度2 060 MPa,弹性模量118 000 MPa,文献[16] FRP抗拉强度1 430.7 MPa,弹性模量118 000 MPa,核心混凝土直径100 mm,混凝土28 d立方体抗压强度34.9 MPa,弹性模量32 800 MPa,L1-0.3 FRP壁厚0.111 mm,作用荷载100 kN,L2-0.3FRP壁厚0.222 mm,作用荷载150 kN。本文建立的组合柱在轴压下的徐变公式考虑的参数包括:玻璃纤维管管壁厚度、混凝土强度等级、混凝土直径、作用荷载等因素,通过图3的对比可知,试件在不同纤维壁厚、混凝土直径、混凝土强度及作用荷载条件下,计算曲线与试验曲线吻合良好,说明利用编制的徐变分析程序对玻璃纤维管钢筋混凝土空心组合柱进行轴压荷载下不同纤维壁厚、混凝土强度、混凝土直径及作用荷载下的徐变性能分析是可行的。
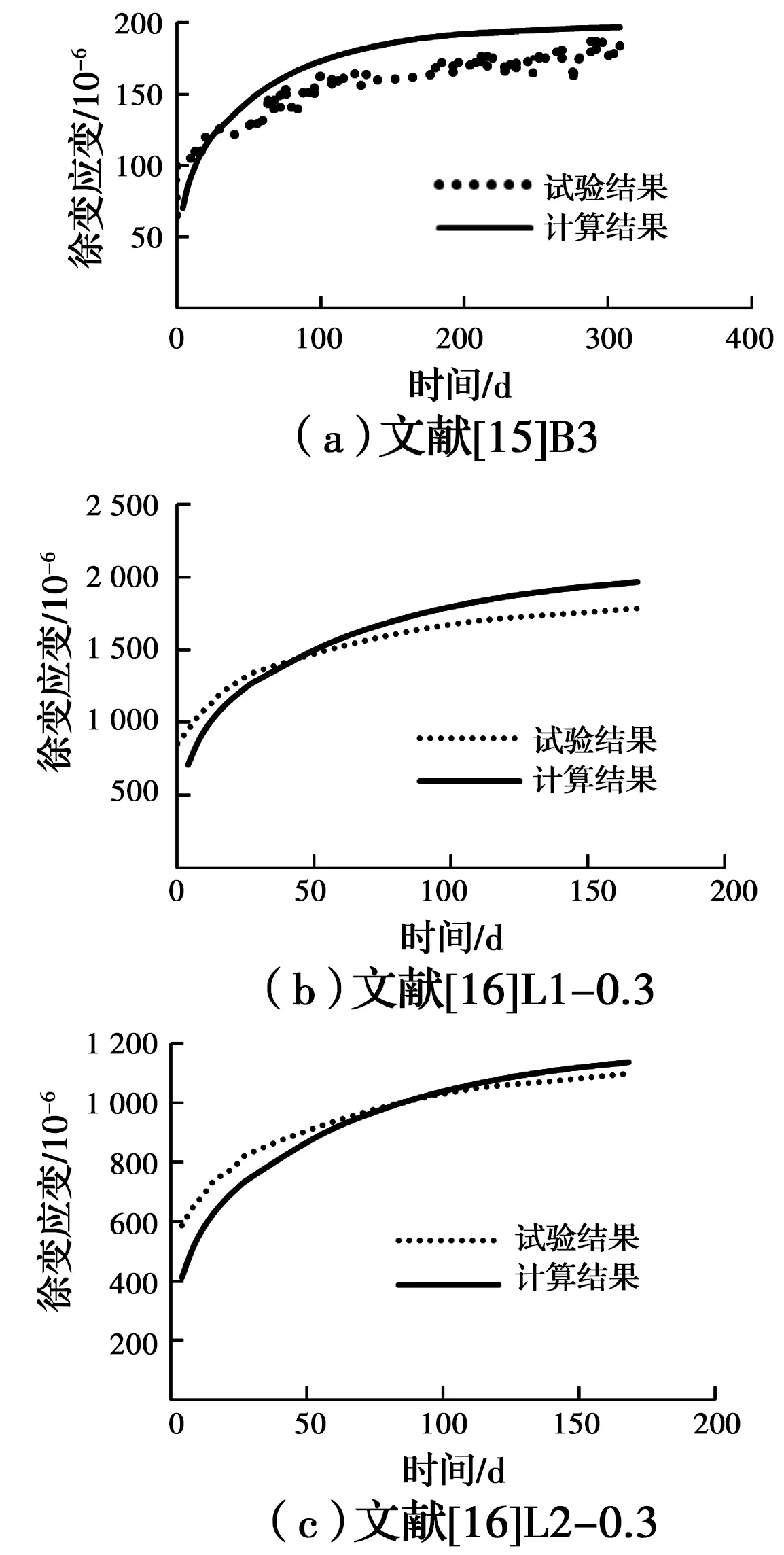
图3 计算结果与试验结果对比图Fig.3 The comparison diagram between calculated
3.2 设计参数的影响
计算采用的基本参数:玻璃纤维管内径200 mm,管壁厚度5 mm,玻璃纤维管环向弹性模量Ef3=61 099 MPa,环向泊松比μf3=0.39,纵向弹性模量Ef1=22 925 MPa,纵向泊松比μf1=0.147,混凝土C30,空心部分混凝土半径50 mm,纵筋4Φ12。在其他参数不变的情况下,通过改变空心率、作用荷载、混凝土强度和玻璃纤维管壁厚等参数,计算其对该空心柱轴压下徐变性能的影响。
3.2.1 徐变对混凝土应力的影响 从图4中可以看出混凝土应力随时间的变化规律,混凝土的应力随时间逐渐减小,混凝土处于持续卸载状态;从图5中可以看出,徐变应变与混凝土应力基本呈线性关系,徐变应变随混凝土应力的减小而增大。
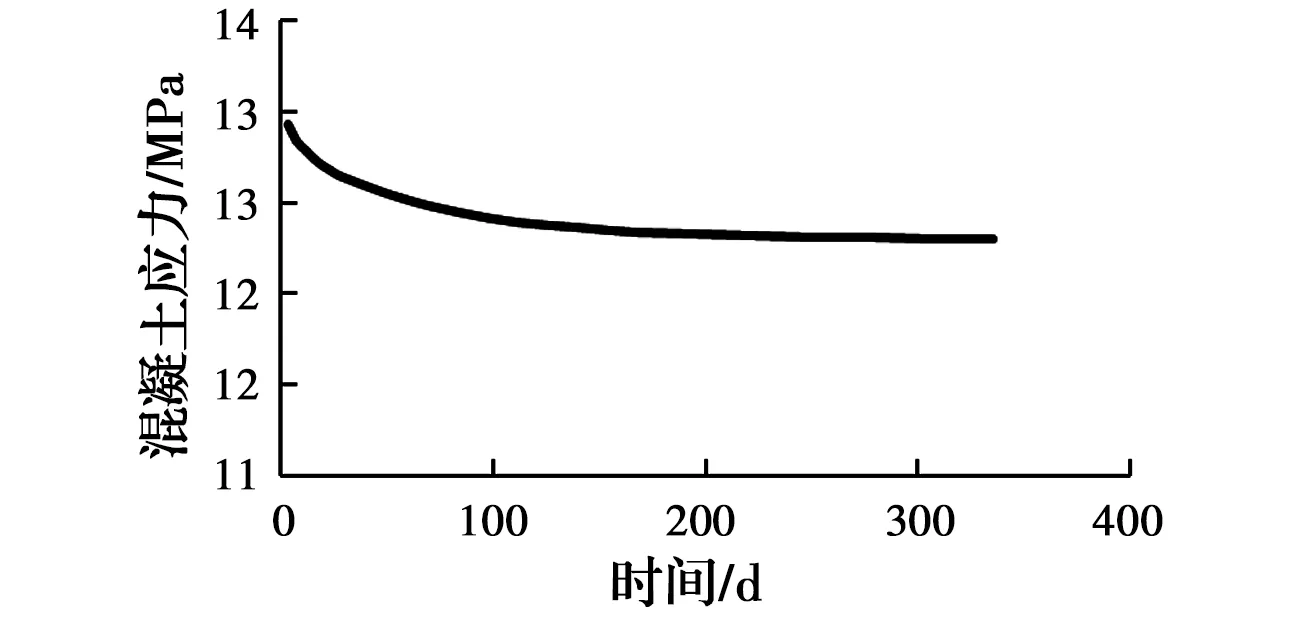
图4 混凝土应力随时间变化曲线Fig.4 Curve of concrete stress changing with
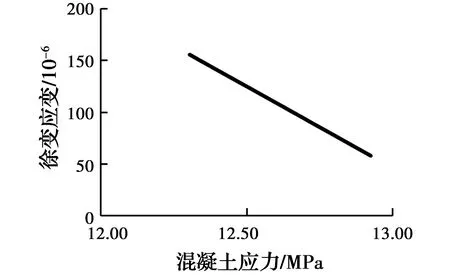
图5 徐变与混凝土应力关系图Fig.5 Relationship between creep and concrete
3.2.2 空心率的影响 采用编制的空心柱轴压下徐变计算分析程序,计算空心部分半径rh分别为75、50、25、0 mm(实心)的徐变应变-时间关系曲线,见图6。从图中可以看出,空心柱的徐变应变随空心率的增大而增加。原因是玻璃纤维管对混凝土的约束作用随着空心率的逐渐减小而相应增加,造成空心柱徐变应变降低。空心部分半径rh为75、50、25 mm的徐变应变比实心0 mm的徐变应变分别减小1.9%、1.2%和0.6%。
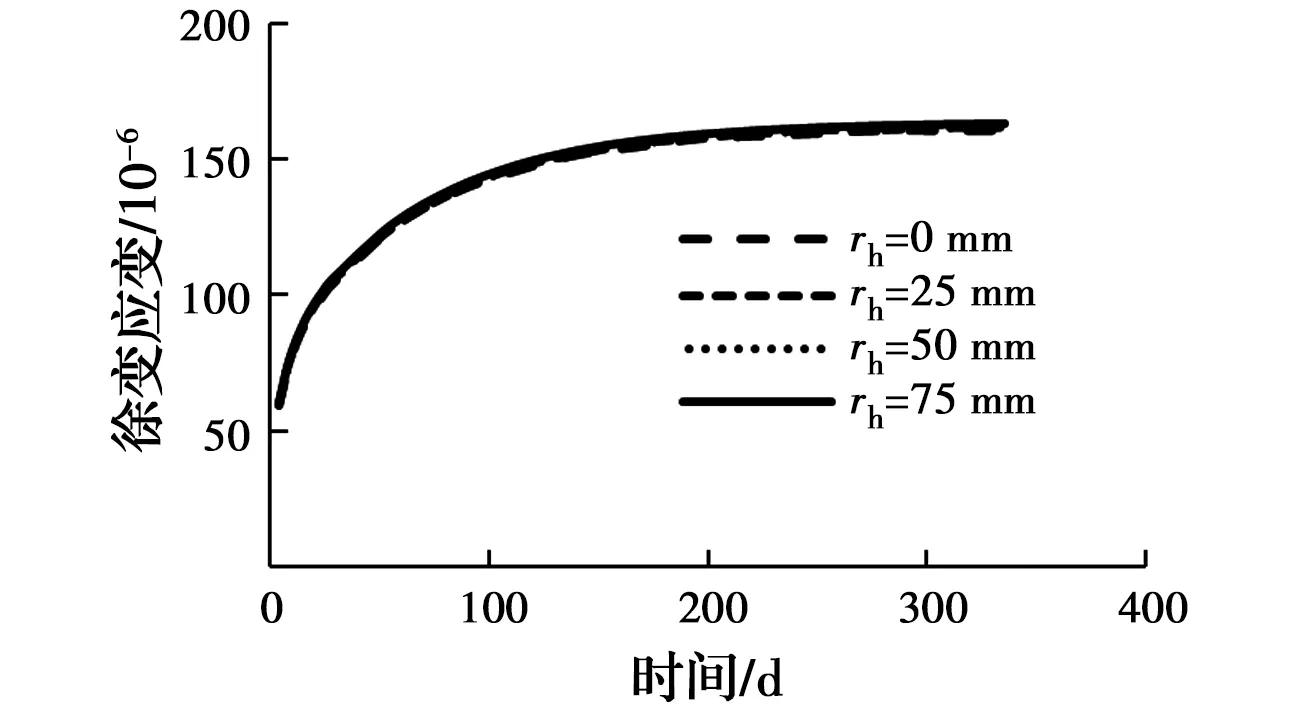
图6 空心率的影响Fig.6 The influence of hollow
3.2.3 混凝土强度等级的影响 采用编制的空心柱轴压下徐变计算分析程序,计算混凝土强度分别为C70、C60、C50、C40和C30的徐变应变-时间关系曲线,见图7。从图中可以看出,空心柱的徐变应变随混凝土强度等级的逐渐增加而相应降低。原因是混凝土的徐变随着混凝土强度等级的逐渐提高而相应降低,造成空心柱的徐变应变降低。混凝土强度C70、C60、C50和C40的徐变应变比C30的徐变应变分别减小4.3%、3.7%、2.6%和1.2%。
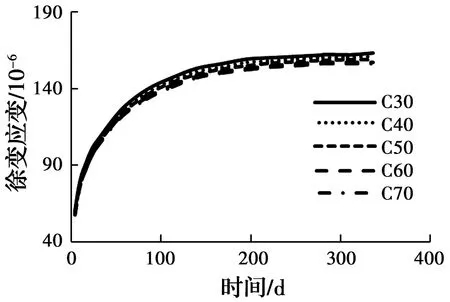
图7 混凝土强度等级的影响Fig.7 The influence of strength grade of
3.2.4 作用荷载的影响 采用编制的空心柱徐变计算分析程序,计算荷载分别为700、600、500、400、300 kN时的徐变应变-时间关系曲线,见图8。从图中可以看出,空心柱的徐变应变随作用荷载的增大而增加,因为混凝土受到的应力随作用荷载的逐渐增大而相应增加,造成空心柱的徐变应变增加。作用荷载为700、600、500、400 kN的徐变应变比作用荷载300 kN的徐变应变分别增大133.6%、99.8%、67.0%和33.2%。
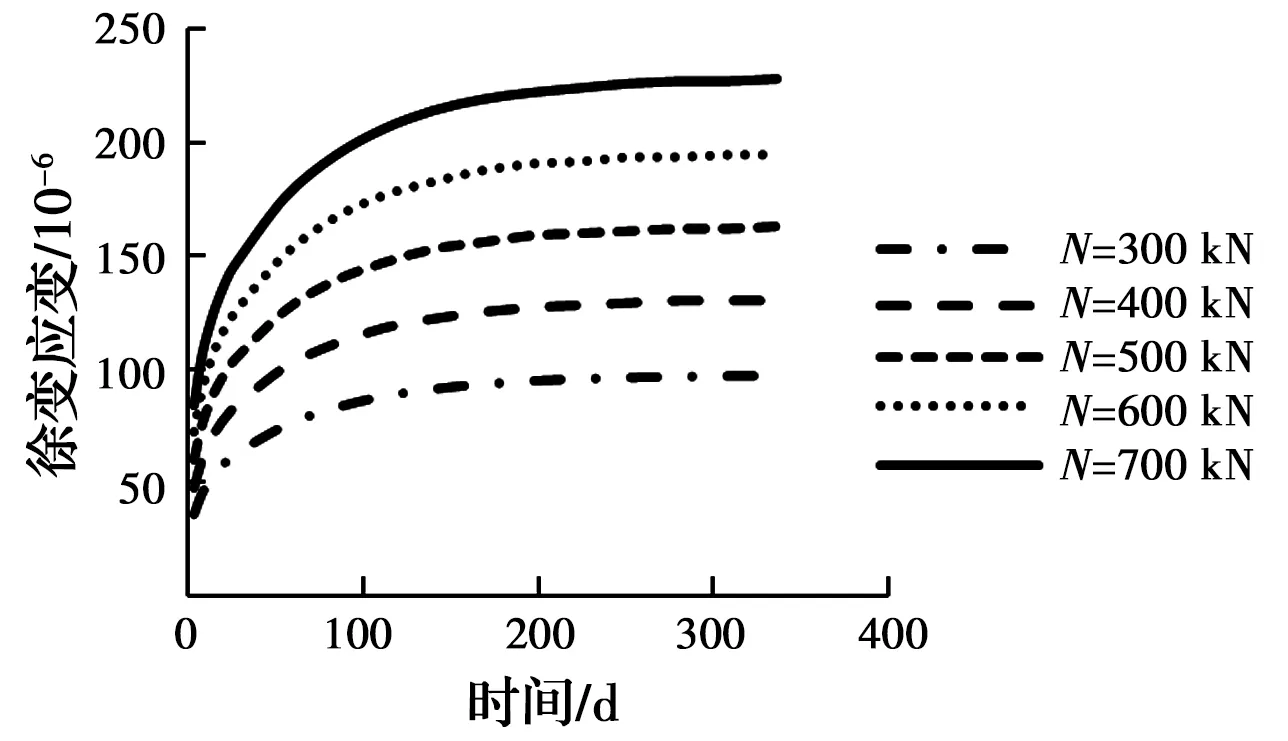
图8 作用荷载的影响Fig.8 The influence of action
3.2.5 玻璃纤维管管壁厚度的影响 采用编制的空心柱徐变计算分析程序,计算壁厚tf分别为7、6、5、4、3 mm的徐变应变-时间关系曲线,见图9。从图中能够得知,空心柱的徐变应变随管壁厚度的增大而减小。因为玻璃纤维管的约束力随着壁厚tf的逐渐增加而相应增大,混凝土的作用相对变小,造成空心柱的徐变应变逐渐减小。壁厚tf为7、6、5、4 mm的徐变应变比壁厚tf为3 mm的徐变应变分别减小19.5%、8.9%、3.6%和1.2%。
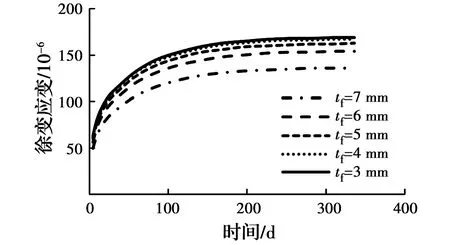
图9 玻璃纤维管壁厚的影响Fig.9 The influence of tube wall
由上述分析可知,玻璃纤维管钢筋混凝土空心柱轴压下的徐变应变随空心率的增加而增加,当空心部分半径rh从75~0 mm,徐变应变减小1.9%;随混凝土强度的增大而减小,当混凝土强度从C30到C70,徐变应变减小4.3%;随作用荷载的增大而增加,当作用荷载从300~700 kN,徐变应变增大133.6%;随玻璃纤维管壁厚tf的增大而减小,当壁厚tf从3~7 mm,徐变应变减小19.5%。空心率和混凝土强度对空心柱轴压徐变影响较小,其次是玻璃纤维管壁厚,作用荷载对其徐变影响较大。
4 结论
1)根据轴压下玻璃纤维管钢筋混凝土空心柱的受力特点,依据混凝土的多轴应力和继效流动理论建立了考虑玻璃纤维管约束力时空心柱轴压徐变计算公式,该公式可以用来预测玻璃纤维管钢筋混凝土空心柱及玻璃纤维管混凝土柱轴压荷载作用下的徐变曲线。
2)根据建立的公式编制轴压徐变分析程序,计算分析徐变应变-时间关系曲线,得到空心柱的徐变应变在28 d以内增长较快,28 d以后增长速度相对缓慢,徐变应变大约6个月以后趋于稳定。并通过已有试验对徐变程序进行验证。
3)在此基础上,计算分析主要设计参数对空心柱轴压徐变的影响。空心率和混凝土强度对空心柱轴压徐变影响较小,其次是玻璃纤维管壁厚,作用荷载对其徐变影响较大。

