酸性环境下砂岩腐蚀的渗流特性

霍润科，钱美婷，李曙光，熊爱华，丁凡，张茹萍

(1. 西安建筑科技大学 a.土木工程学院；b. 陕西省岩土与地下空间工程重点实验室，西安 710055；2.中铁二十局集团有限公司 高原隧道施工技术及装备研发中心，西安 710016)

随着现代工业的迅速发展，酸性环境污染已经成为工程建设中不容忽视的破坏因素，作为一种边坡工程中常见的非均质材料，砂岩内部含有大量随机分布的微裂隙、孔洞、界面等缺陷，这些不连续的缺陷构成了砂岩多相复合的结构特征，从而影响砂岩的宏观物理性质，使其力学性能呈现各向异性、非线弹性和时效性[1]。随着CT技术的快速发展，其应用范围逐渐拓宽，学者们开始利用CT扫描技术探究受酸腐蚀砂岩截面的物质组成、孔隙结构等岩心参数，分析酸性环境变化对砂岩腐蚀过程的影响。

早期数字岩心技术多选用数值建模方法，主要基于电镜的二维扫描图，通过随机法或过程模拟等数值模拟算法实现三维重构[2]。Øren等[3]提出过程模拟法，考虑岩石基质的粒径分布，模拟真实岩心形成的过程，重现岩石真实的传导性质和几何属性；Hazlett在Metropolis和Kirkpatrick模拟退火算法的基础上，将目标函数定义为重建介质与模拟介质性质差值的平方和，通过体系更新，使其逐渐稳定，从而实现数字岩心；Okabe等[4]提出多点地质统计法，巧妙运用地质信息，利用二维岩心薄片，解决数字岩心重构过程中的连通性难题，随后孙建孟等[5-7]开展孔隙网络流动模拟研究。在Berea[8-10]数字岩心的理论基础上，刘洋等[11]将数字岩心技术应用于研究低渗储层岩石的渗流机理，分析流体在油湿和水湿两种环境下的饱和状态，并判断其饱和度的区别；孙泽[12]在Berea构建的砂岩孔隙网络模型的基础上利用CT扫描技术对致密岩样进行数字岩心重建，提取孔隙度、孔喉大小、连通系数等岩心数据及孔隙空间分布状态图；李江涛等[13]利用格子方程模拟页岩气宏观尺度的渗流模型，解释滑脱效应和气井产量与地层能量之间产生的联系；Qiu等[14]、何雅玲等[15]通过对孔隙网络的三维动态模型进行微干扰测试，研究流动状态下润湿度及孔隙率对毛管数的影响规律；唐明明等[16]利用数字岩心和格子玻尔兹曼建立了致密砂岩的驱替模型，对比不同注入条件下驱替参数的变化及驱替过程的影响。

综上所述，数字岩心孔隙网络模型主要应用于细观渗流特性的研究，而对于酸性环境下岩石的腐蚀研究几乎尚未涉及。笔者从孔隙角度出发，选用砂岩作为试验对象，分析其在不同浓度的酸性条件下孔隙率及渗流特性的变化规律。

1 试验方案

选用陕西省某水利工程中矿物成分含量已知的长石砂岩作为试验研究对象，砂岩的矿物组成以石英(58%)和长石(11%)为主，填隙碎屑中包含方解石(5%)、硅质岩屑(6%)、硅铁质胶结物(7%)、云母(3%)、灰质岩屑(2%)、黏土杂基(3%)、绿泥石(1%)等矿物，偶尔会出现帘石、磷灰石等重矿物(4%)，颗粒之间的胶结类型主要呈现为孔隙式胶结。从砂岩岩块中钻取两组h=100 mm、Ф=50 mm的标准圆柱体试样，采用全浸法分别浸泡在pH值为1、3两种浓度的硫酸溶液中，为了加快酸腐蚀进程，每隔30 d更换一次硫酸溶液。每组试验配备多个容器作对照分析，确保试验的准确性。室内模拟砂岩受酸腐蚀的加速试验如图1所示。

图1 室内模拟砂岩的酸腐蚀加速试验Fig.1 Acid corrosion acceleration test of simulated

浸泡180 d后，岩样表面及酸性溶液中不再出现明显化学腐蚀现象，从两组酸性溶液中取出岩样，烘干后沿纵向1/2处横切开，可看出岩样横截面出现明显的腐蚀区和未腐蚀区。考虑到岩样密度较大，CT扫描试验过程中可能会影响X射线探测器对信号的接受，故屏蔽X射线，另一方面，在分析图像数据的过程中，岩样尺寸越大，图像的分辨率会越低，所以不宜选用尺寸过大的岩样进行岩心CT扫描试验。

从腐蚀岩样的腐蚀区和未腐蚀区选取5个不同的位置钻取岩心试样，岩心尺寸为长7 mm、直径3.5 mm的小圆柱体岩样，岩心试样及取样位置示意图如图2所示，分别用S、X、C、B、Z表示。

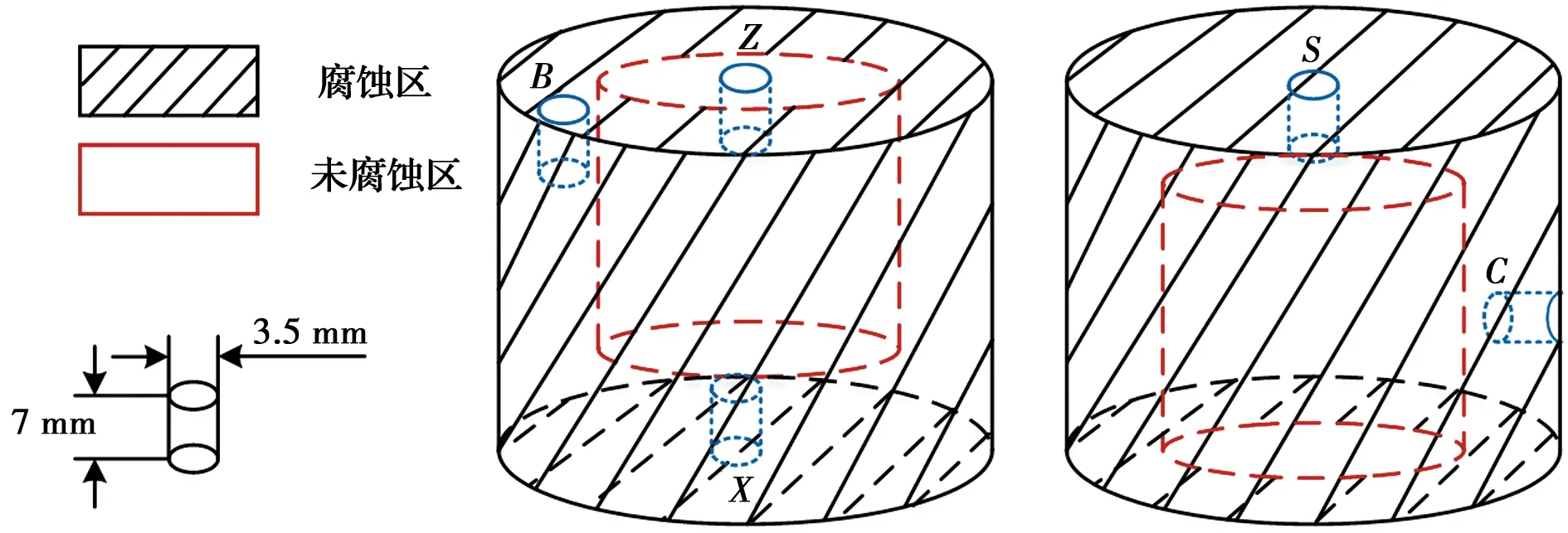
图2 岩心试样及取样位置示意图Fig.2 Schematic diagram of core sample and sampling

CT扫描试验采用高分辨率三维X射线CT扫描设备(Zeiss Xradia 510 Versa)，扫描过程中的试验参数分别为：90 kV电压、7 W功率、岩样与光源相距15.015 mm、岩样与探测器相距18.486 mm、1 s曝光时间、1 h总时长。CT扫描结束后，每块岩心可获得800张像素为2 025×2 025的二维切片图，CT图像的分辨率为2.47 μm/像素，格式为BMP。

2 研究对象的建立

为了从获得的二维切片图像中完成数据重建，提取与孔隙结构相关的细观信息，需要通过无损伤的图像处理技术去除干扰信息，突出有效信息，并为下一步能够更精确地分割孔隙和骨架奠定基础。CT扫描试验是通过X射线透过待测岩样，在岩样与空气接触的边缘区域，X射线的衰减强度会表现出岩体到空气的过渡现象，不会出现明显的分界，通常会比较模糊，这对岩心孔隙和骨架的区分非常不利。利用图像切割消除边界伪影的影响，表征真实岩心的内部孔隙结构，文中截取体素为740×740×740的立方体区域进行图像处理。图像预处理方法主要包括亮度调整、对比度调整、图像锐化及降噪处理等，图像处理技术均基于Image J软件完成。

预处理前后的直方图对比图如图3所示。由图3可以看出，相较于原始图像，直方图的灰度值区域从[0,80]扩展到[0,130]，频数峰值对应的灰度值从48平移至75，边缘信息得到了强化，图像的整体质量得到了提高。

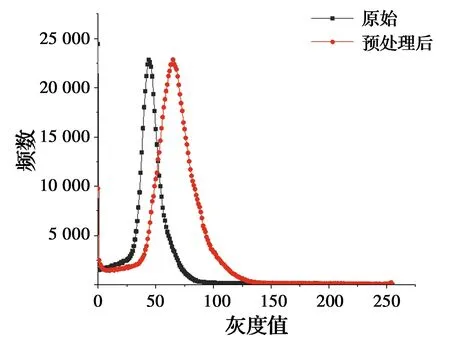
图3 预处理前后的直方图对比图Fig.3 Histogram comparison before and after

通过中值滤波对岩心图像实现降噪处理，可以在不损坏图像的前提下提高信噪比、衰减噪声，同时保留重要信息。然后采用迭代阈值法选取合适的分割阈值。计算步骤如下：

1)首先确定一个初始阈值T，通常选择像素的平均灰度值μ作为初始阈值；

2)通过阈值分割将图像分成G1和G2两部分，利用式(1)计算出G1和G2区域的平均灰度值μ1和μ2

(1)

式中：i为区域内的灰度值，p(i)为灰度值的概率；

3)利用式(2)确定新的阈值T′，

T′=(μ1+μ2)/2

(2)

4)重复步骤2)和3)，直到T′不发生变化为止，此时的T′即为最终确定的分割阈值。

最终计算出岩心图像的分割阈值T′=27，二值化处理后得到的结果如图4所示，其中黑色代表孔隙，白色代表岩石骨架。将阈值分割后的CT图像导入Avizo软件中，利用Volume Rendering模块将孔隙结构可视化，通过Edit New Label Field模块对岩样的骨架和孔隙空间进行数据组合，三维重建后得到真实岩心的数字化表征，即数字岩心。其中29-Z岩样的三维数字岩心模型如图5所示。

图4 岩心图像的二值化结果Fig.4 Binary results of core

图5 29-Z岩样的三维数字岩心模型Fig.5 3D digital core model of 29-Z

3 渗流模型的构建

砂岩试样是一种含有大量孔隙的多孔介质，在三维数字岩心的基础上，利用格子Boltzmann模型可以将不规则的孔隙空间划分成规则的格子网络，将酸性溶液离散成一个个均匀分布的流体粒子，构建渗流模型描述离散粒子在真实岩心中的运动模式，简化数字岩心的空间计算，扩宽模型的研究意义，完成不同酸性环境下砂岩受酸腐蚀的渗流特性研究。

3.1 格子Boltzmann方程

格子Boltzmann是通过演化粒子间的分布函数，对宏观的运动特性进行描述的一种数值模拟方法，本文模拟对象为三维的数字岩心。因为砂岩的孔隙率较低，二维的格子Boltzmann模型无法对其内部的孔隙结构进行准确地描述，所以选用三维的格子Boltzmann模型-D3Q19(图6)对受酸腐蚀砂岩的孔隙空间实现数值模拟，初始孔隙率选用上表面和侧面C岩样孔隙率的平均值，即浸泡在pH值为1酸性溶液中的岩样孔隙率为2.90%，浸泡在pH值为3酸性溶液中的岩样孔隙率为2.30%。

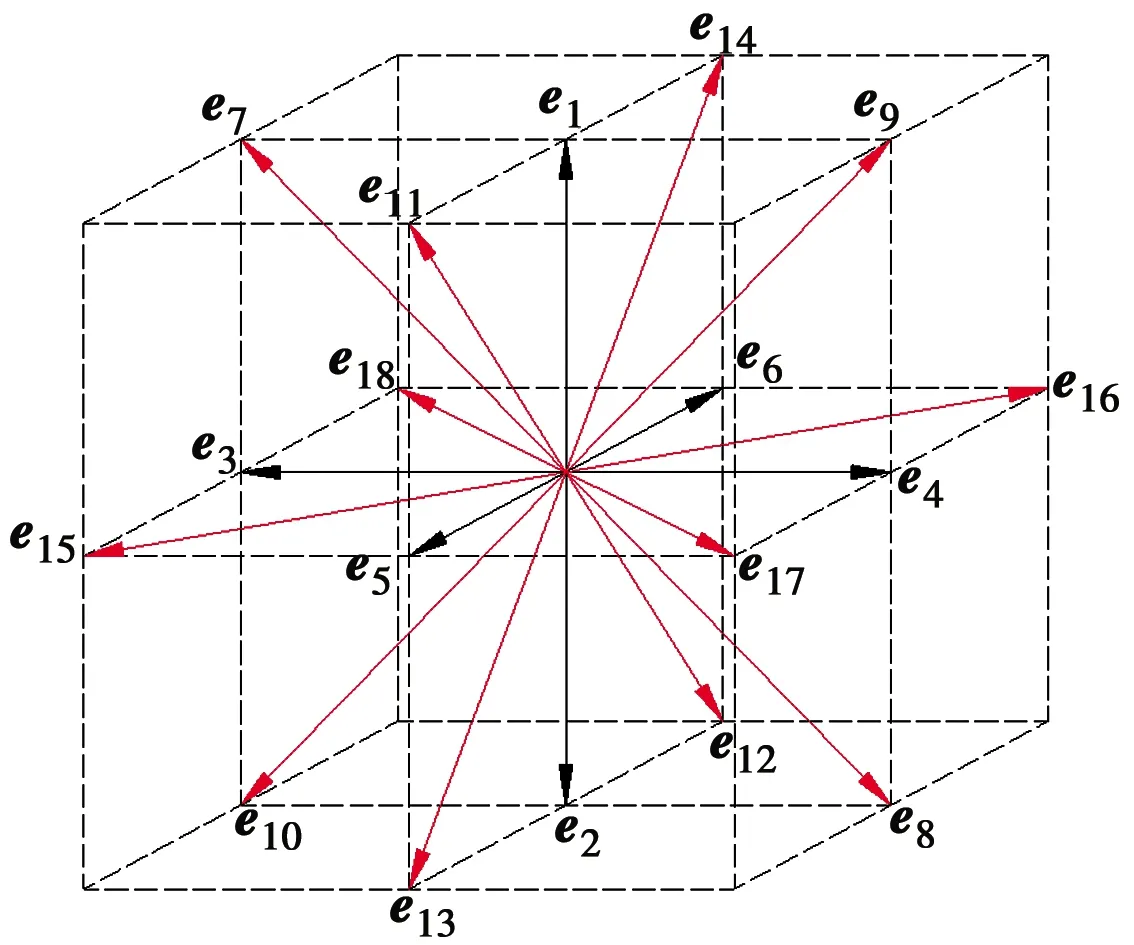
图6 D3Q19格子模型

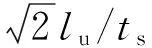
19个速度矢量具体分量表达式为

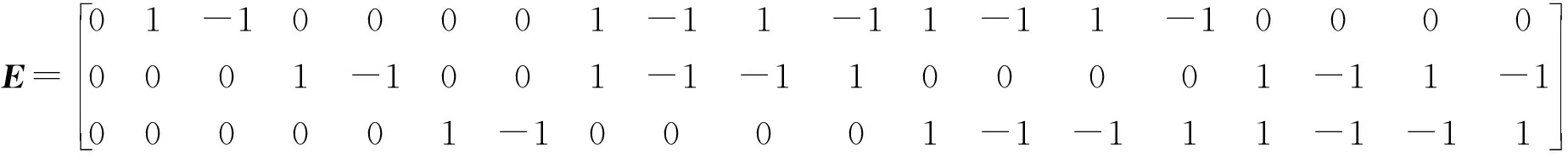
根据质量和能量守恒定律，格子上粒子的宏观密度μ和宏观速度υ分别为

(3)

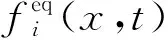
(4)

式中：tσ为权系数，与速度矢量的长度有关，具体数值为

(5)

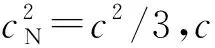
解得

(6)

i=1,…,6

(7)

i=7,…,18

(8)

3.2 边界处理

选用D3Q19模型，数值模拟过程中，将岩石骨架与孔隙交界处设置无滑移的反弹边界，出入口均采用定压边界，设yz平面为孔隙流体的输入端，且流体沿y轴和z轴的速度分量均为0，即vy=vz=0，则D3Q19模型的压力边界条件计算式为

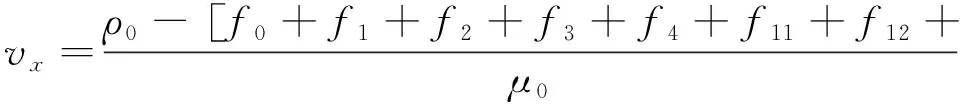
(9)

(10)

(11)

(12)

(13)

3.3 设定初始变量

建立的数字岩心是一个像素为740×740×740的立方体，其中x=0的yz平面为酸性溶液的注入端，x=740的yz平面为酸性溶液的流出端，其他4个平面均为砂岩骨架。假设在初始状态下，砂岩注入端的孔隙空间均被酸性溶液填满，酸性溶液在化学腐蚀的作用下沿着x方向渗流。基于数字岩心模型，结合格子Boltzmann方程，模拟砂岩内部H+的渗流过程。其中格子模型的分辨率为2.47×10-9m，物理空间的模拟步长为1×10-7m，物理时间的模拟步长为1×10-9s，格子速度的特征值为1×10-5，物理速度的特征值为1×10-3m/s。

D3Q19模型中，粒子黏度λ的公式为

λ=(2τ-1)/6

(14)

式中τ为弛豫(松弛)时间。

粒子间压力P与宏观密度μ的关系式为

(15)

3.4 模拟过程

1)读取数字岩心孔隙模型的数据，其中0为孔隙，1为岩石骨架；

2)选用D3Q19模型划分孔隙网格，并设定弛豫(松弛)时间τ及黏度参数λ等宏观物理参数；

3)计算各节点速度矢量的初始分布函数；

4)设定边界处理形式：对骨架与孔隙的交界处执行无滑移的反弹边界，出入口执行定压边界；

5)迭代粒子间碰撞和迁移的两个运动状态；

6)计算宏观变量，并判断模型是否满足平衡条件(式16)；

(16)

7)若满足平衡条件，则输出计算结果；若不满足，重复步骤3)～6)；

4 结果分析

4.1 CT试验结果分析

通过高精度的CT扫描试验，获取真实的岩心数据，直观描述了不同浓度酸性环境下砂岩受酸腐蚀的内部孔隙分布。从二维切片图(图7)可以看出，砂岩的横断面紧密排列着很多矿物质，均具有不同程度的亮度表现，其中亮度高的为高密度区，亮度低的为低密度区。砂岩的矿物组成中，云母的密度最大，对应亮度最高的区域，分割阈值为T′=150；其次是石英和长石，密度小于云母，对应二维图像中的灰度区域，阈值范围为[40，130]，含量约为73%；亮度最低且接近黑色的区域对应密度最小的孔隙，分割阈值为T′=27。CT扫描试验中获取的切片图像可以展示非均质砂岩内部的矿物组成结构及孔隙空间的分布情况。

图7 岩心切片的二维CT扫描图Fig.7 Two-dimensional CT scans of core

腐蚀区和未腐蚀区中钻取的岩样在二维图像中也表现出明显的差异性。未腐蚀区岩样的岩心图像表现出矿物排列致密、孔隙含量较少的内部结构，而腐蚀区岩样的岩心图像则表现出矿物排列稀疏、孔隙含量较高的内部结构。这是由于酸性溶液对不同位置的腐蚀程度不同，以及矿物耐酸腐蚀能力的差异性所致。

4.2 基于数字岩心分析受酸腐蚀砂岩的孔隙率变化

砂岩孔隙率α可表示为

(17)

式中：V孔为砂岩内部孔隙的总体积；V总为砂岩的表观体积。

编号为29的岩样是在pH值为3的硫酸溶液中浸泡180 d后的岩样，编号为WC-6的岩样是在pH值为1的硫酸溶液中浸泡180 d后的岩样，两种岩样上表面、下表面、侧面C、侧面B和中间5个不同位置处孔隙率的对比如图8所示。从图8中可以看出，高浓度的酸性溶液对砂岩的腐蚀程度整体高于低浓度的酸性溶液，其中29号岩样上表面和侧面C位置的孔隙率最大，分别为2.632%和2.658%，其次是下表面和侧面B两个位置的孔隙率为2.065%和1.943%，最小孔隙率出现在中间位置，仅为1.092%；WC-6号岩样侧面B位置的孔隙率，为4.253%，是腐蚀过程中出现的最大孔隙率，其次，上表面和侧面C两个位置的孔隙率均为3.025%，然后是下表面的孔隙率，为2.803%，最小孔隙率出现在中间位置，为1.038%。

图8 不同位置处岩心孔隙率的对比图Fig.8 Comparison of core porosity at different

两块岩样的最小孔隙率均出现在中间位置，说明经过180 d的浸泡，两种浸泡溶液中的岩样均未被酸性溶液完全腐蚀，中间位置仍保持初始状态；酸性溶液的浓度不同，形成的腐蚀程度不同，在pH值为1的硫酸溶液中浸泡180 d的岩样，下表面位置形成的孔隙率为2.803%，而在pH值为3的硫酸溶液中浸泡180 d的岩样，形成的孔隙率仅为2.063%，酸性溶液的浓度越高，对该位置砂岩腐蚀形成的孔隙率越高；与酸性溶液发生直接接触的岩样和未发生完全接触的岩样之间会出现孔隙率差值，在pH值为1硫酸溶液中浸泡180 d的岩样，上表面和侧面C两个位置与下表面位置形成的孔隙率差值为0.22%，在pH值为3的硫酸溶液中浸泡180 d的岩样，形成的孔隙率差值为0.59%，酸性溶液的浓度越高，孔隙率差值越小；从图7中可以看出，上表面位置的WC-6-S岩心试样中存在高密度矿物，对酸性溶液的渗透腐蚀形成阻碍，而侧面B位置的岩心试样颗粒间孔隙分布较均匀，腐蚀程度较强，所以在砂岩侧面B位置出现最大孔隙率的现象。

4.3 渗流模型结果分析

应用格子Boltzmann法构建酸腐蚀砂岩在酸性溶液中的渗流模型，计算出不同酸性环境下编号WC-6和29这两块岩样的渗透深度，上述两块砂岩的数字岩心均是基于X射线的CT扫描试验建立得到的，浓度不同的硫酸溶液在砂岩中的渗透深度随砂岩孔隙率的变化规律如图9所示。

图9 浓度不同的硫酸溶液中渗透深度随砂岩孔隙率的变化规律Fig.9 Permeability depth of sulfuric acid solution with different concentration varies with porosity of

图9中曲线为格子Boltzmann方程求解渗透深度数据点的拟合曲线，可以看出，浓度不同的硫酸溶液在砂岩中的渗透深度随砂岩孔隙率的变化规律基本保持一致，渗透深度随着孔隙率的增大而增大，变化速率先快后慢，最后趋于稳定。砂岩与酸性溶液接触的初始阶段，内部孔隙空间会发生剧烈的化学反应，导致酸性溶液的渗透深度增加较快；随后，酸性溶液中H+的浓度降低，砂岩内部Na+、K+、Mg2+、Ca2+等阳离子逐渐被置换出来，形成胶结物，阻碍了酸性溶液对其进一步腐蚀，酸性溶液在岩样中渗透深度的增长速率逐渐放缓，最后趋于稳定。

4.4 格子模型的适用性验证

利用单轴压缩试验分别对自然状态下的未腐蚀岩样和在酸性环境下浸泡t天的腐蚀岩样施加外荷载P(t)，岩样的受力荷载模型如图10所示。图中，σ(0)为自然状态下未腐蚀岩样的单轴抗压强度，MPa；σ(t)为酸性环境下浸泡t天后腐蚀岩样的单轴抗压强度，MPa；d(0)、d(t)分别为砂岩受酸腐蚀前后的直径，mm；阴影部分为腐蚀区。假设砂岩试样为各向同性的均质体，扩散作用沿径向发展，腐蚀区的岩样骨架不承受荷载作用。

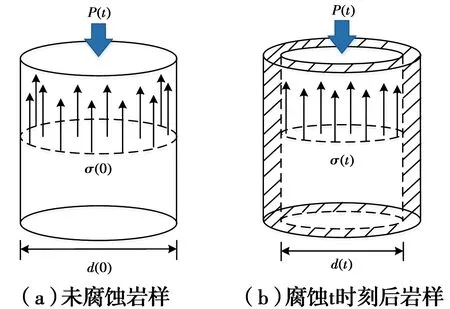
图10 砂岩在外荷载作用下的物理力学模型Fig.10 Physical and mechanical model of sandstone

单轴压缩过程中，砂岩承受的外荷载P(t)可以表示为[17]

(14)

可得，

(15)

因此，受酸腐蚀岩样的渗透深度x(t)可表示为

(16)

砂岩试样的单轴压缩试验结果见表1。

表1 单轴压缩试验结果Table 1 Uniaxial compression test results

将试验数据代入式(16)可得在pH值为1、3的硫酸溶液中浸泡180 d岩样的渗透深度分别为4.54、3.96 mm。对比格子Boltzmann方程构建的数值模型计算的两种酸性环境下的渗透深度分别为4.23、3.97 mm，发现计算渗透深度的模拟值和试验值基本保持一致，说明基于格子Boltzmann方程构建的数值模型对模拟砂岩受酸腐蚀过程的渗流特性具有较好的适用性。

5 结论

利用CT扫描试验和Avizo软件，对受酸腐蚀砂岩的内部孔隙结构进行可视化表征，建立数字岩心，分析砂岩受酸腐蚀过程中不同位置孔隙率的变化特征，结合格子Boltzmann模型和单轴压缩试验，探究受酸腐蚀砂岩的渗流特性及腐蚀过程中渗透深度的变化规律。得到以下结论：

1)高精度的CT图像中可通过灰度值的变化判断砂岩内部的物质组成，其中云母对应灰度值最高的区域，分割阈值为T′=150；石英和长石对应灰度区域，阈值范围为[40，130]，含量约为73%；亮度最低且接近黑色的区域对应密度最小的孔隙，分割阈值为T′=27，从而展示非均质砂岩内部的矿物组成结构及孔隙空间的分布情况。

2)腐蚀条件一致，腐蚀程度基本一致，反之，砂岩内部会出现大小不同的孔隙率差值，酸性溶液的浓度越高，形成的孔隙率差值越小。溶蚀砂岩的速率随酸性溶液浓度的增大而增大，pH值为1的硫酸溶液溶蚀砂岩后，岩样下表面位置的孔隙率为2.803%，pH值为3的硫酸溶液溶蚀砂岩后，岩样下表面位置的孔隙率为2.063%。

3)砂岩渗透深度随孔隙率的增大而增大，变化速率先快后慢，最后趋于稳定。pH值为1、3的硫酸溶液的渗透深度分别为4.23、3.97 mm，单轴压缩试验中渗透深度的试验值分别为4.54、3.96 mm，说明基于Boltzmann方程构建的渗流模型对模拟砂岩受酸腐蚀过程具有较好的适用性。