VCO-ADC非线性数字校准算法及FPGA验证

佟星元，杨 梅

(西安邮电大学 电子工程学院，陕西 西安 710121)

模/数转换器(Analog-to-Digital Converter, ADC)主要通过对输入信号在模拟域和基准进行比较的方式完成模拟输入信号数字化[1]，以便于随后的数字信息加工及处理。基于压控振荡器(Vol-tage-Controlled Oscillator, VCO)的ADC是一种常用的模/数转换器类型，其利用VCO将ADC的输入信号从电压域信息转换到时间域信息。随着ADC输入信号的改变，VCO输出信号频率和周期发生相应的变化，通过在一个采样周期内统计VCO脉冲的个数获得最终的数字输出。VCO的电压/频率特性曲线存在非线性，会降低VCO-ADC的信噪失真比(Signal to Noise and Distortion Ratio, SNDR)和无杂散动态范围(Spurious Free Dynamic Range, SFDR)[2]，影响模/数信息转换的准确度。针对VCO-ADC的非线性校准方法进行研究尤为重要。

现实中，通常的做法是将VCO作为反馈回路中的积分器，提供一个大的环路增益，以减小ADC的非线性[3]，该方法需要模拟支持电路，并且反馈电路中的数模转换器(Digital-to-Analog Converter, DAC)和额外的模拟放大器或积分器导致整体电路设计复杂[4]。基于最小均方根(Least Mean Square, LMS)算法校准技术能够明显改善VCO-ADC的线性性能[5]，该方案采用了一个4位Flash ADC，增大了电路面积。经典的查找表(Look-Up Table, LUT)校准算法校准效果较好，但是需要额外的调制器和一条复制电路路径才能确定校准参数[6]。基于LUT的非线性校准算法，以抖动信号作为校准算法的前提，使用LMS反馈回路确定校准参数，完成LUT线性插值，得到正确输出码[7-9]。这种校准算法不需要模拟电路支持，校准参数的确定不需要复制电路路径，还可以满足不同输入信号的校准需求，是一种新兴的VCO-ADC的非线性校准方法，越来越引起研究者的关注。但是，该算法存在消耗资源过多的缺点。

为了降低电路中的资源消耗，在VCO-ADC非线性校准方法的基础上，主要采用加法运算，以节省大量硬件资源消耗，并且选择较少的LUT点数。此外，采用现场可编程门阵列(Field Programmable Gate Array, FPGA)片外校准方法，以满足在校准算法的选取和修改上的灵活度要求。

1 VCO-ADC原理及其非线性

1.1 VCO-ADC基本原理

经典的非线性VCO-ADC整体电路原理示意图如图1所示。非线性VCO-ADC整体电路由两个VCO-ADC子通道A和B构成，每个通道分别采用差分结构实现VCO-ADC[10]。利用伪随机噪声码(Pseudo Random Noise, PRN)分别为A、B通道两端Vn、Vp添加正、负扰动信号pΔV/2，其中，p=±1表示信号的正负属性，ΔV表示添加的扰动电压。正负扰动信号相差180°。通过采样保持(Sample/Hold, S/H)电路后A、B两个通道的差分理想输出电压分别为VinA和VinB。VinA和VinB经过非线性VCO、计数器和减法器输出数字码nA和nB。

图1 非线性VCO-ADC电路原理示意图

对于理想ADC，两个ADC输出的平均值为最终数字输出码xout，但是，在实际电路中会存在非线性问题。nA、nB通过LUTA和LUTB完成线性插值，得到xA、xB。校准信号Δx为xA、xB的差值。若两个ADC的输出能够被正确地校准，则得到的校准信号Δx=2pD，其中D为扰动电压ΔV经过ADC后得到的信号值；反之，则Δx≠2pD，需要通过校准调整每个ADC的值，使得Δx趋近于2pD，从而使得ADC的误差趋近于0，最终得到正确的数字输出码，完成校准过程。

采用差分结构的VCO-ADC可以有效抑制共模干扰和偶次谐波，从而为整个系统的线性提供保障，减小后续非线性校准算法的工作量。

1.2 VCO-ADC非线性

VCO-ADC将采样后的输入信号作为VCO的输入控制电压，完成电压-频率转换，理想情况下，t时刻VCO的实时输出频率为

fvco(t)=fc+kvVin(t)

其中：fc表示自由振荡频率；kv表示VCO的增益；Vin(t)表示t时刻的输入控制电压。

t时刻VCO的输出电压为

Vo(t)=Avcocosθvco(t)

其中：Avco表示VCO输出的幅值；θvco(t)表示t时刻VCO的实时输出相位，为VCO输出频率的时间积分，即

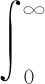
但是，在实际电路中，VCO-ADC存在非线性问题，主要体现在VCO的输入控制电压与实时输出频率不成正比。时间电路t时刻VCO的实时输出频率为

其中，ki(i=1,2,…,5)表示第二阶到六阶的畸变项。

畸变项的存在表明VCO频率存在奇偶非线性，导致VCO输出的正弦振荡信号中存在谐波，以此振荡信号作为计数器的计数时钟，则会导致最终的数字输出也存在非线性。

VCO非线性模型示意图如图2所示。理想VCO和非线性VCO的模型的输出电压频率曲线如图3所示，从图中可以很明显地看出实际VCO的非线性特征。

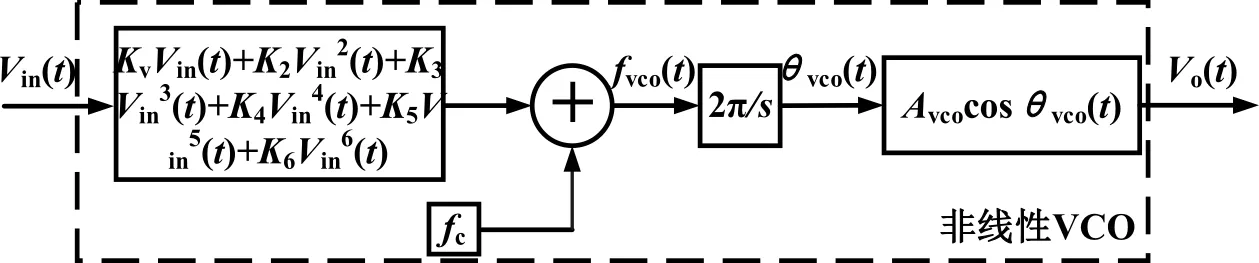
图2 非线性VCO的模型示意图

图3 VCO输出电压频率曲线

1.3 VCO-ADC非线性的抑制技术

改进VCO电压频率曲线的非线性的常用技术是差分结构方法，但是，差分结构方法只能在一定程度上改善ADC的非线性，通常还需要采用抑制技术进一步降低ADC的非线性。经常被使用的抑制技术有以下3种。

第一种抑制技术基于DAC的闭环反馈，由差分反馈回路中的两个VCO组成[11]。VCO由输入差分信号与转换后的数字输出反馈之间的差值驱动。两个VCO的输出驱动一个计数器，利用得到的相位差使回路趋向平衡。该结构类似一个具有大环路增益的控制回路，在VCO输入节点处进行转换运算，从而大大降低了VCO非线性的影响。

第二种抑制技术是一种粗量化和细量化结合的技术，其运算过程为一种闭环结构[12]。输入信号首先被一个粗量化器量化，产生一个粗糙的数字输出结果。其次，将该数字输出结果通过DAC转换得到一个模拟量，将该模拟量从输入信号中减去，得到一个低摆幅残差信号，这个残差信号驱动细量化器工作，得到数字输出结果。最后，将经过粗量化器得到的数字输出和细量化器得到的数字输出相加从而得到最终的量化结果。

第三种抑制技术是数字校准技术。将输入信号通过非理想VCO-ADC产生带有误差的数字输出码，采用VCO的复制路径提取VCO非线性的估计值。将该估计值作为校准信号，采用连续的自适应数字校准算法，以减少VCO-ADC的非线性[13]。

前两种非线性抑制技术都需要DAC电路，会增加电路面积和电路设计的复杂度，而校准技术无须使用DAC电路，相对更加简便。

2 非线性数字校准算法

2.1 非线性校准算法原理

非线性校准算法原理示意图如图4所示。图4分为上方虚线框中的转换部分和下方实线框中的校准部分。

图4 非线性校准算法的原理示意图

在转换过程中，首先，对输入信号Vin进行采样，并根据PRN扰动信号产生VinA和VinB，然后，经VCO和计数器模块转换，产生带有误差的数字码nA、nB，并作为算法的输入。

在校准过程中，首先，利用LUT线性插值模块分别得到与数字码nA、nB相对应的LUT中的位置，再进行线性插值得到与数字码nA、nB相对应的校准输出码xA、xB。然后，使用LUT线性插值模块得到与数字码nA、nB相对应的矩阵系数yA、yB，构建估算矩阵Y，得到校准信号Δx=xB-xA。利用YT和Δx-2pD做乘法运算得到对应的误差向量，用以更新LUT中的相关数据，从而构成LMS的反馈环路，如图4中所示。其中，μ值取2-7为步长因子，其大小由LMS算法决定[14]。

根据得到的查找表的最新数据，采用线性插值方法更新xA和xB，对Δx和2pD的差值进行判决，若判决结果不为0，则继续循环上述步骤，直到差值为0，输出校正值xA和xB。由于使用了两个VCO-ADC，难以抉择出选哪一个更适合作为最终的输出，所以需要以两个ADC输出的平均值作为校准后的输出码，从而得到输出码x=(xA+xB)/2[15]。

2.2 非线性校准算法LUT建立和线性插值

查找表线性插值原理示意图如图5所示。LUT中取值个数由ADC的精度和VCO的电压-频率特性曲线决定。

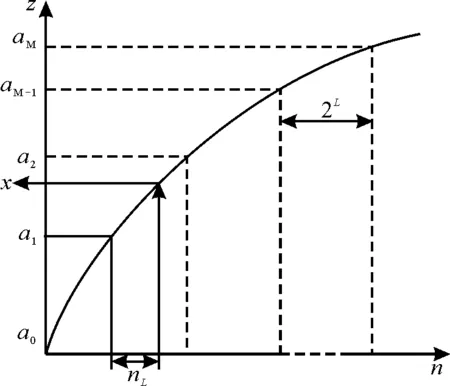
图5 查找表线性插值原理示意图

校准算法的目的是确定图5中LUT中的值ai(i=0,1,2…,M)的传输特性。首先，将校准算法的输入n分为M位高有效位nM和L位低有效位nL，并将M作为LUT的地址。高有效位决定了LUT中的点数N(N<2M)，对于每一个nM，都有一个与之对应的校准输出码anM。然后，在每个部分中，低有效位nL作为anM和anM+1之间的插值。n轴点与点之间的间距为2L，通过线性插值得到校准后的输出码

2.3 非线性校准算法功能仿真

在Modelsim仿真平台上对非线性校准算法系统进行仿真，观测输入输出波形，以验证校准算法的功能。校准算法功能仿真流程示意图如图6所示。首先，使用硬件描述语言Verilog HDL编写校准算法的LUT线性插值模块、随机序列产生模块、LUT参数输入和更新模块、DIF模块Δx-2pD、LMS模块和输出模块x=(xA+xB)/2的硬件描述语言，并利用软件Modelsim对各模块完成功能仿真验证。其次，在顶层模块中，对各个模块进行实例化，应用仿真软件Matlab建模非线性VCO-ADC，并将得到的输出作为校准算法的输入，写入*.txt文本。最后，编写Testbench，对*.txt文本中的数据进行读取，完成校准电路设计和功能仿真。

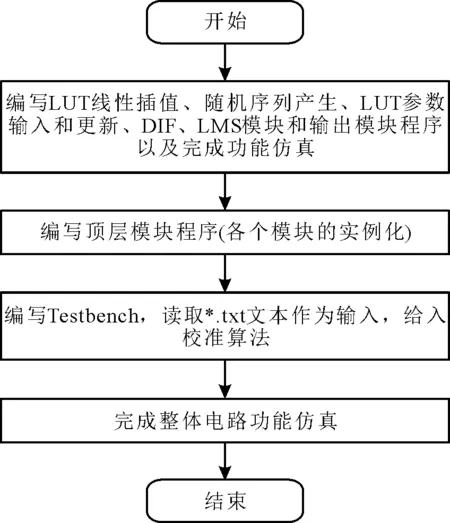
图6 校准算法功能仿真流程示意图

3 FPGA验证及分析

3.1 FPGA验证

在功能仿真的基础上，采用FPGA开发板对校准算法实施硬件验证。在FPGA硬件验证过程中，需要使用分频模块、地址产生模块和只读存储器模块。分频模块为地址产生模块、只读存储器模块和整个校准电路提供时钟。地址产生模块用于产生只读存储器模块所需的10进制地址。只读存储器模块用于存储Matlab建模产生的10位VCO-ADC输出。

在Quartus II 13.1使用Verilog HDL语言完成硬件电路的设计，程序通过USB-Blaster下载至Cyclone IV系列EP4CE30F23C8开发板，使用Quartus II 13.1中的SignalTap II Logic Analyzer对输入输出信号进行实时监测，并对数据进行保存输出，进行后续频谱分析。

3.2 结果分析

使用Matlab对带有非线性的VCO-ADC进行建模，基于10位ADC模型验证选取校准算法的效果。对ADC进行仿真，并结合Matlab对ADC仿真得到的4 096个采样点进行快速傅里叶变换(Fast Fourier Transformation, FFT)分析，得到ADC的输出频谱图。10位VCO-ADC校准前、后的频谱图分别如图7和图8所示。可以看出，相较于校准前的频谱图，由于采用差分结构和校准算法，抑制了偶次谐波，去除了奇次谐波，并且导致噪声底板有所下降。

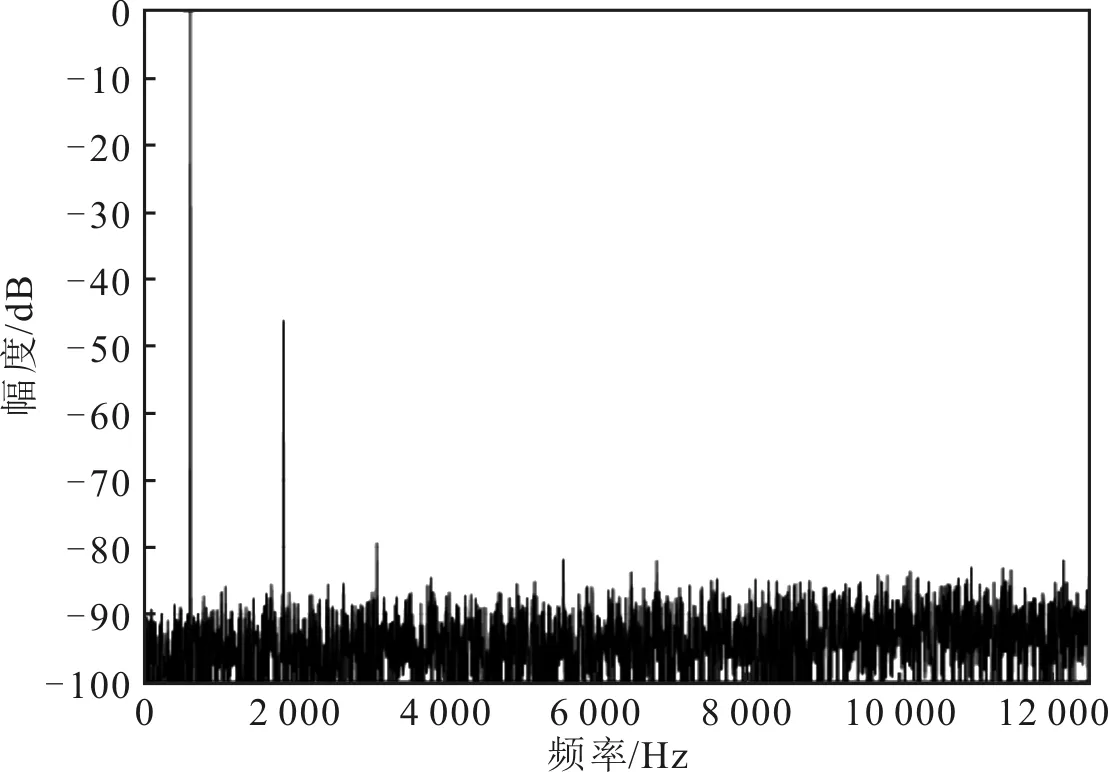
图7 校准前的VCO-ADC频谱图

图8 校准后的VCO-ADC频谱图

经过测试发现，在校准之前，由于受到VCO非线性影响，ADC的有效位数(Effective Number of Bits, ENOB)仅为7.33，SNDR仅为45.92 dB，SFDR为46.15 dB。校准后的频谱，ENOB从7.33提升至9.46，SNDR提升至58.73 dB，SFDR为85.24 dB。说明校准算法能有效降低ADC的各次谐波和噪声。这是因为SNDR表示输出信号的基波信号功率与所有噪声总功率的比值，当所有噪声总功率减小时，SNDR增大。ENOB由SNDR计算得到，当SNDR增加时，ENOB也增加。SFDR是输出信号的基波信号功率与最大谐波功率的比值，当最大谐波功率减小时，SFDR会变大。

利用斜坡输入信号，仿真得到微分非线性(Differential Non-linearity, DNL)和积分非线性(Integral Non-linearity, INL)。校准前、后的DNL和INL的值分别如图9和图10所示。可以看出，校准前后DNL的取值范围分别为-1～+1.73 LSB和-0.14～+0.71 LSB。校准前后INL的取值范围分别为-3.59～+17.43 LSB和-0.46～+1.35 LSB。说明校准算法减轻了实际数字输出与理想数字输出之间的差异，改善了ADC的非线性问题。

图9 VCO-ADC校准前后的DNL

图10 VCO-ADC校准前后的INL

所提方法与其他校准算法的性能参数对比如表1所示。可以看出，所提校准算法校准前、后SNDR的提升与其他校准算法校准前、后SNDR的提升幅度相当，但是，SFDR提升幅度明显，这是因为所提校准算法对ADC最大谐波的抑制能力强。另外，虽然其他3个文献的方法均采用数字校准算法降低了ADC的非线性，但都需要模拟电路的支持。这会增加电路面积和电路设计的复杂度，而实现的数字校准算法，则不需要模拟电路的支持。

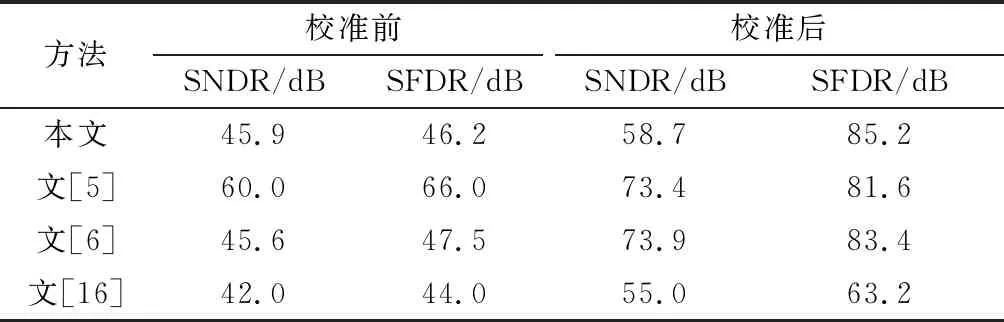
表1 不同校准算法的性能参数对比

4 结语

针对VCO非线性影响VCO-ADC的线性性能问题，构建了一种10位VCO-ADC模型，并完成了功能仿真和FPGA验证。利用LUT线性插值模块得到数字码在LUT中相对应的位置，执行线性插值获取对应于数字码的校正值及相关的估算矩阵。利用校正值得到校准信号，将估算矩阵转置和校准信号相乘，以获取相应的误差向量，并更新LUT中的相关数据，构成LMS反馈环路。根据LUT的最新数据，采用线性插值获取最新的校正值，并最终输出正确的校正值。所提校准算法可以有效提高ADC的ENOB、SNDR和SFDR，并且降低了ADC的DNL和INL。