一种多目标的可见光DCO-OFDM系统优化方案

寇艳春，李连本，田 原，张之栋，黑永强

(1.中国移动通信集团 陕西有限公司，陕西 西安 710077;2.中国移动通信集团设计院有限公司 陕西分公司，陕西 西安 710077;3.西安电子科技大学 综合业务网理论及关键技术国家重点实验室, 陕西 西安 710071)

随着发光二极管(Light Emitting Diode, LED)技术与固态照明技术的迅速发展，可见光通信(Visi-ble Light Communication, VLC)技术为当前通信频谱短缺的现状提供了一种可能的解决方案[1-2]。与射频通信系统相比，VLC系统具有频谱资源巨大和不受电磁干扰等明显优势，在智能家居、医院机器人和井下作业等众多场景中有着广泛的应用前景。

在VLC系统中，由于LED技术存在带宽有限和室内多径传播延迟等问题，导致在高数据速率下会引起严重的符号间干扰(Inter-Symbol Interfe-rence, ISI)现象。为了克服ISI，正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)技术被应用于VLC系统中[3]。LED本身固有的特性要求通过其信号为正实数，所以衍生出了直流(Direct Current, DC)偏置光OFDM(DC-Biased Optical OFDM, DCO-OFDM)技术、非对称削波光OFDM(Asymmetrically Clipped Optical OFDM, ACO-OFDM)技术与翻转光OFDM(Flip-OFDM)，这些技术手段原理不同，但是都可以保证通过LED的信号满足正实数的要求[3-5]。由于操作方便并且谱效较高等原因，使得DCO-OFDM技术受到了广泛的关注[3-5]。

目前，对DCO-OFDM可见光通信系统的研究多集中在谱效与能效提升方面。在提升谱效方面，通过采用分层ACO-OFDM技术[6]和负混合ACO-OFDM技术[7]获得更高的谱效。另外，随着大型移动设备带来的巨大能源消耗问题变得越来越严重，研究的重点逐步从对谱效优化的研究转向对能效优化的研究。随后，各种节约能效的优化方法开始出现，例如，通过调整发射功率与分配系统带宽[8-9]以及选择合适的子载波调制阶数[10]，能够使得可见光系统获得更高的能效。

目前的研究多数关注谱效或能效两者其中的一个方面，统筹兼顾两者的研究较少。为此，文献[11]推导了可见光通信系统中谱效和能效折中的闭合表达式，但是该文献构建的信道模型没有考虑实际LED的有限带宽，而且对如何克服ISI和增强谱效关注不足。

针对LED的有限带宽，拟提出一种兼顾谱效和能效两个指标的可见光DCO-OFDM通信系统的优化方案。依据实际通信系统传输场景，选用合适的DCO-OFDM调制方式并考虑LED有限带宽，建立DCO-OFDM系统谱效和能效的表达式。同时，采用多目标优化的思想，将谱效或能效两个优化目标通过权重因子汇聚成一个优化目标，根据实际应用场景的需求灵活改变权重因子值，从而实现能效与谱效性能的统筹兼顾。

1 系统模型

在DCO-OFDM系统中发射端的光学器件一般采用LED来实现电光转换，接收端的光学器件一般采用光电二极管来实现光电转换[3]，整个DCO-OFDM系统原理框图如图1所示。首先，输入的二进制数据经过正交幅度调制星座映射后，对通过串并变换和共轭对称操作获得的频域信号进行N点的傅里叶逆变换(Inverse Fast Fourier Transform, IFFT)处理，N为总载波数。其次，对时域的OFDM信号进行并串转化，同时增加循环前缀和数模转化。最后，给获得的双极性时域信号叠加一个直流偏置使其转化为单极性实值信号，从而可以驱动LED将所要传输的信息以光的形式发射出去。在接收端，使用光电二极管对接收的光信号进行直接检测，即将接收到的光强度转化为电信号的幅值。然后，这个接收端将按照发射端的逆过程解调出所发送的数据。

图1 VLC中DCO-OFDM原理框图

为了满足经过IFFT变换后得到的时域信号为实数信号，图1中DCO-OFDM系统中采用的原始OFDM频域信号需要满足的条件为

(1)

其中：(·)*表示共轭操作；[·]T表示转置操作；Xk为第k(k=1,2,L,Nt)个子载波上的频域信息，Nt=N/2-1表示有效的子载波数。

频域信号执行N点傅里叶逆变换后变为时域OFDM符号，再通过添加循环前缀和通过数模转换操作，获得双极性的时域OFDM实信号为

(2)

式中，xk(n)表示第k个子载波上的时域OFDM实信号。

在双极性时域OFDM实信号xu(n)上施加一个直流正偏置xDC，可以获得一个正实信号为

x(n)=xu(n)+xDC

(3)

为了方便分析和推导，假设LED从开启电压(Turn On Voltage, ToV)到最大允许电压均在线性范围内，则LED线性区域电流与电压的关系示意图如图2所示[11]。设置当信号电压小于开启电压时，信号电流为0；当信号电压大于开启电压时，信号电流大于0。另外，信号电压最大不能超过最大允许电压。

图2中的Ur为LED开启电压，Umax为最大允许电压，Imax为最大允许电流，U为电压，I为电流。则图2斜率可以表示为

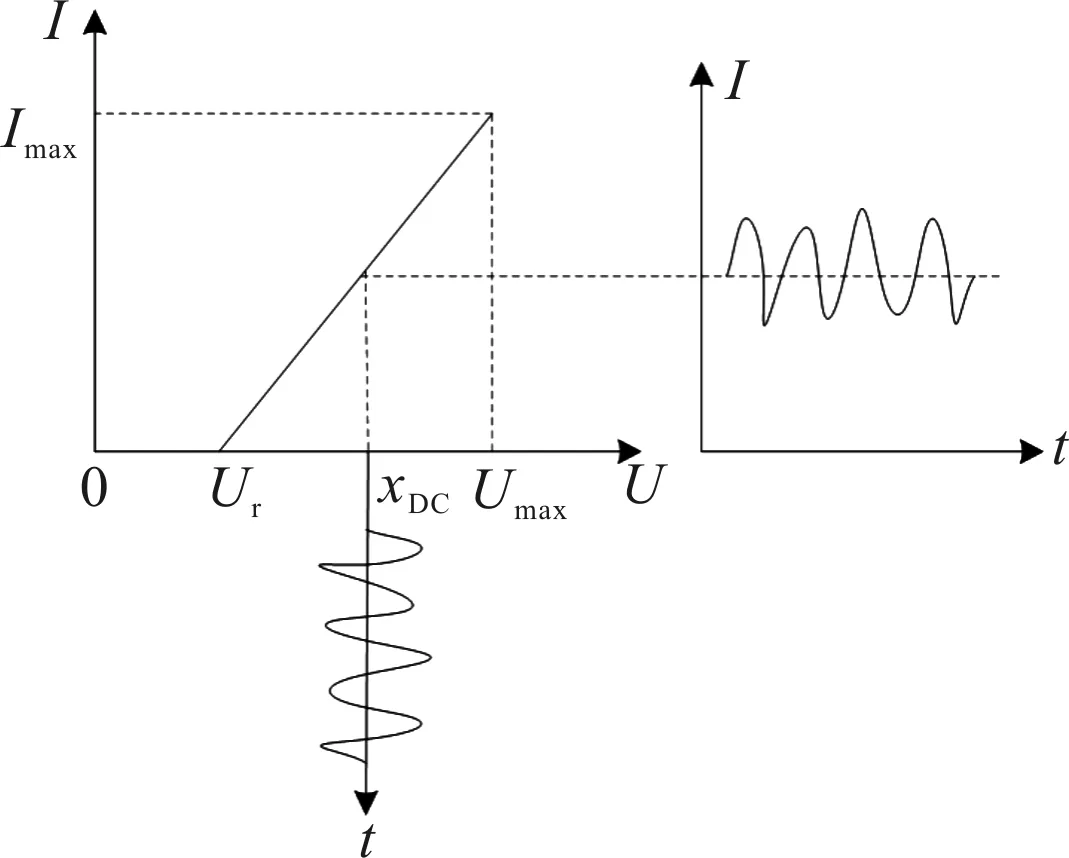
图2 LED线性区域电流与电压的关系示意图

k1=Imax/(Umax-Ur)

直流偏置通常被选择为LED线性区域的中点[11]，则直流偏置的取值为

(4)

在可见光DCO-OFDM系统中，因为所需的循环前缀长度与傅里叶逆变换的长度相比起来很短，可以忽略循环前缀对DCO-OFDM系统的影响[12]。

在接收端，通过执行与发送端逆过程得到原始信号，第k个子载波上接收的频域信号可以表示为

Y(k)=RpdX(k)H(k)+Z(k)

(5)

式中：Rpd表示光电二极管的响应度；Z(k)表示第k个子载波上的接收端频域噪声；X(k)表示第k个子载波上的频率响应；H(k)表示第k个子载波上的DCO-OFDM信道的频率响应。

为了使信道更符合实际情景，引入了具有表征前端设备LED滤波效果的低通模型来描述DCO-OFDM系统中前端设备的有限带宽，采用一阶函数逼近前端器件滤波的归一化信道增益[13]，其计算表达式为

(6)

其中，Ffe表示由于前端设备的低通滤波而导致的频率响应。f表示频率，定义为

f=kFs/N

其中，Fs代表采样频率。

式(6)中第k个子载波上的归一化信道增益可以表示为

(7)

相应地，等效的VLC信道增益可以表示为

|H(k)|2=|Hfs(k)|2|Hfe(k)|2

(8)

其中，Hfs(k)表示可见光通信系统中自由空间传输的频率响应。

对于任意k，均满足|Hfs(k)|≈Hlos[13]，其中，Hlos表示发射机LED到光电二极管的直流信道增益[13]。

2 基于比特功率加载技术的能谱效

信噪比在通信系统中具有重要作用。根据式(5)可以计算出第k个子载波上的接收信号的信噪比为

(9)

式中：Pele,k表示第k个子载波上的发射功率，即电功率；σ2=N0Wsc表示高斯白噪声方差。其中，N0表示高斯白噪声的功率谱密度，Wsc表示子载波的带宽。

总发射功率

Pele,AC=

由于OFDM子载波的正交性，所以总发射功率又可以表示为

Pele,AC=

谱效通常被定义为每单位带宽上所能传输的数据速率。要想提高频谱利用率，应该尽量增加总数据传输速率。DCO-OFDM系统因为受到LED有限带宽的影响通常难以获得高谱效，为此，将比特功率加载技术[14]引入到DCO-OFDM系统中。比特功率加载技术所要达到的目标是在给定总发射功率的条件下，通过为各个子载波分配功率，从而使得通信系统在满足一定服务质量(Quality of Service, QoS)的情况下(通常包括特定前向纠错误码率等要求)，总数据速率达到最大。值得注意的是，此处获取的总数据速率是在连续比特功率负载情况下的理论上限，以总数据速率作为优化目标，以总发射功率和特定前向纠错误码率作为约束条件[5]，优化模型可以表示为

(10)

其中：R表示总数据速率；bk和Bk分别表示第k个子载波的比特数和误码率；BFEC表示前向纠错误码率。

对于式(10)的优化问题，可以利用拉格朗日乘子法可转化为无约束优化问题，拉格朗日函数[15]的定义为

(11)

其中：λ表示拉格朗日乘子；F2(p,b,λ)为无约束优化函数；p=(Pele,1,Pele,2,…,Pele,Nt)为功率矢量；b=(b1,b2,…,bNt)为比特矢量。

在实际应用中，子载波上的调制技术类型一般为正交振幅调制(Quadrature Amplitude Modulation, QAM)方式，则每个子载波上分配的比特数目可以表示为

(12)

其中，Γ表示信噪比间隔。若DCO-OFDM VLC系统各个子信道采用的调制类型相同，且各个子载波的误码率也都相等，则各个子载波的信噪比间隔就都相等。此时的信噪比间隔为一个常数，即

Γ=-ln(5BFEC)/1.5

将式(12)代入式(11)中，可以得到

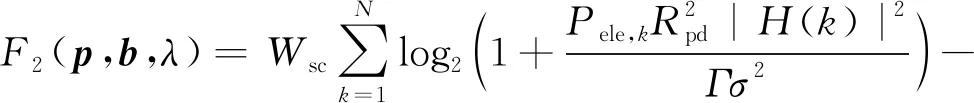
(13)

从式(13)可以看出，F2(p,b,λ)是Nt个自变量{Pele,1,Pele,2,…,Pele,Nt}的多元函数。为了推导最优功率分布和最优比特分布，将F2(p,b,λ)对p中各元素取偏导数并令其等于0，可得

(14)

将式(14)代入式(10)的约束条件，可得

(15)

从式(15)可求解出拉格朗日乘子为

(16)

将式(16)代入式(14)，可以得到使系统传输速率最大的最优功率分布为

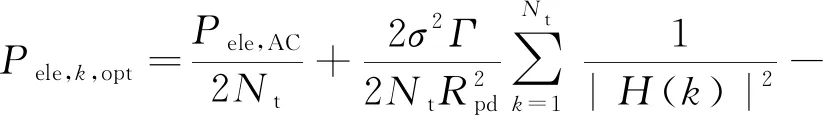
(17)

令拉格朗日函数F2(p,b,λ)对p中各元素取二阶偏导数，可以发现F2(p,b,λ)的海森阵为负定阵。据多元函数极值判定定理，可以得出F2(p,b,λ)存在极大值。又因为F2(p,b,λ)的驻点是唯一的，能够得出F2(p,b,λ)存在最大值且唯一。所以，式(17)中所求得的Pele,k,opt就是使得F2(p,b,λ)取得最大值的唯一解，同时也是使系统传输速率取得最大值的最优功率分布。

将式(17)代入式(12)可以得到最优的比特分布为

(18)

可得，总的数据传输速率为

(19)

(20)

能效作为通信系统对电能使用效率的一个衡量标准，其定义为信息传输速率与总功耗的比值，其计算表达式为

(21)

由于将LED线性区域消耗的功率作为系统的总功耗[11]，可以表示为通过线性LED电压U与电流I乘积的期望。所以，系统的总功耗可以表示为

PLED={UI}=
{(xu(n)+xDC)k1(xu(n)+xDC+Ur)}=
k1xDC(xDC-Ur)+k1
k1xDC(xDC-Ur)+k1Pele,AC

(22)

基于比特功率加载的能效可以表示为

(23)

为了进一步分析基于比特功率加载的谱效与能效分别与发射功率的关系，首先对ηSE关于Pele,AC求导，可得

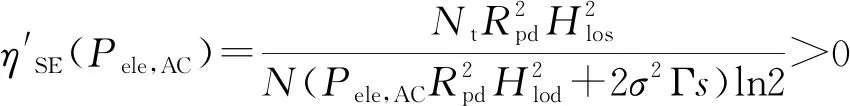
(24)

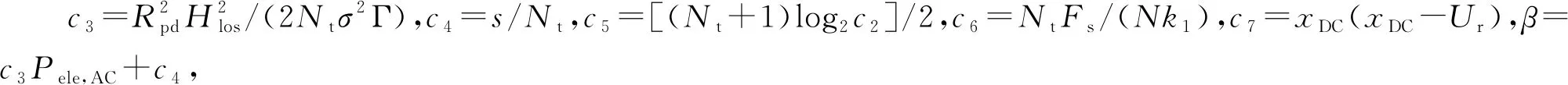
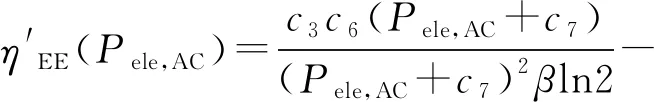
(25)

对f1(Pele,AC)取一阶偏导可得

(26)

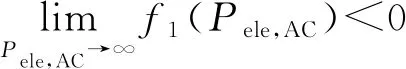
3 基于多目标优化的能谱效折中

能效与谱效随着发射功率的变化趋势并非总是一致，两者之间存在一些冲突，所以需要联合优化。将谱效和能效作为DCO-OFDM系统的两个目标函数，将该系统的多目标优化问题可以描述为优化问题

s.t.Pele,AC∈P

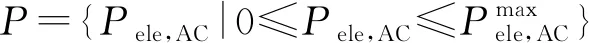
3.1 Pareto最优解

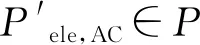
对于优化问题P1中Pele,AC∈P的Pareto最优解集，可以分为下面两种情况进行讨论。

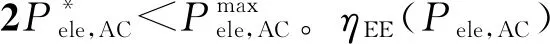
因此，优化问题P1中Pele,AC的Pareto最优解集为

PPOS=

(27)

s.t.Pele,AC∈PPOS

3.2 多目标优化转换单目标优化

为了解决问题P2，引入加权乘积标量方法[17]，其原理为通过给谱效与能效分派不同的权重因子，然后将这两个目标函数通过效用函数聚合成为一个单目标函数。

根据加权乘积标量法的思想设计一个效用函数

U(ηEE,ηSE)=(λSE)ω(λEE)1-ω

(28)

式中，ω∈[0,1]为一个可以表征谱效在效用函数U(ηEE,ηSE)中所占比例的权重因子。

从式(28)可以看出，通过调整ω的值就可以实现对能效或谱效的优化倾向选择，即通过利用效用函数U(ηEE,ηSE)，多目标优化问题P2就可以进一步转化为

此时，优化问题P3已经成为一个单目标优化问题，为了使得优化问题P3的目标函数呈现线性关系，方便后面的计算，对式(28)进行对数操作，即

Z1=lgU=
ωlgλSE+(1-ω)lgλEE=

lgηSE-(1-ω)lg(xDC(xDC-Ur)+Pele,AC)-μ

(29)

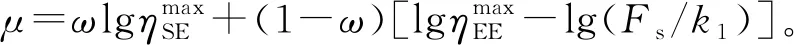
由于Z1为U的对数形式，所以其二者的增减变化同步。因此，单目标优化问题P3可以进一步写成

接下来证明优化问题P4中Z1(Pele,AC)是Pele,AC的严格拟凹函数。证明过程如下。

对优化问题P4中Z1(Pele,AC)取一阶偏导，得到

(30)

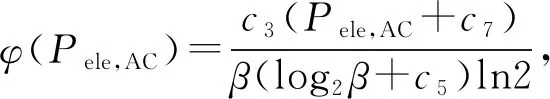
(31)

φ(Pele,AC)=1-ω

(32)

对于1-ω∈[0,1]，下面分成两种情况来进行讨论。

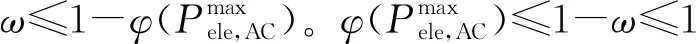
因此，优化问题P4的最优解可以表示为

(33)

4 性能仿真及分析

为了验证所提方法的性能，采用MATLAB软件进行仿真研究。仿真主要参数设置如表1所示。

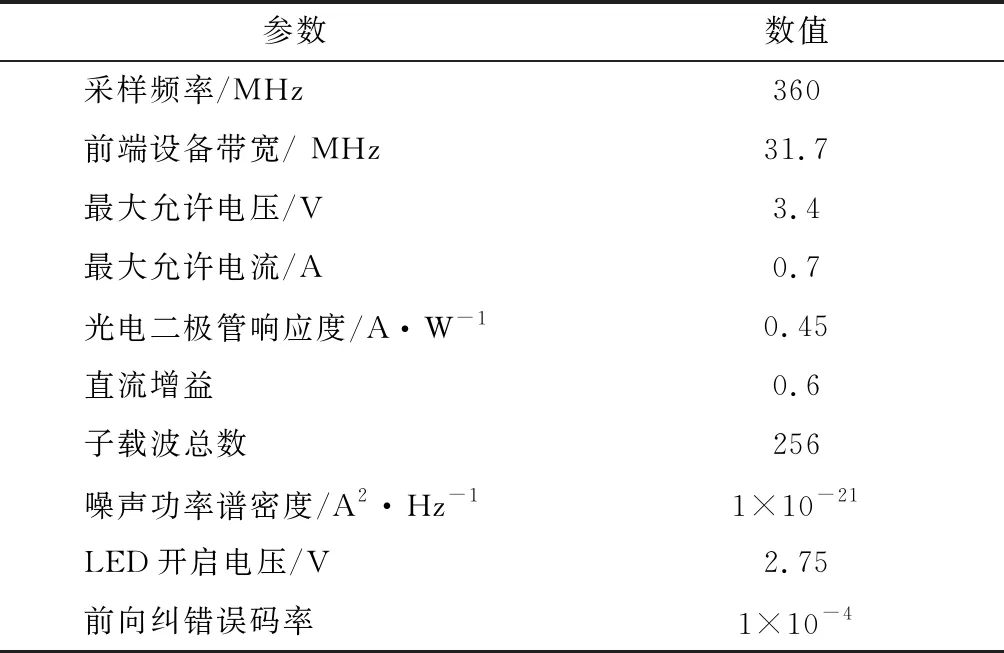
表1 仿真主要参数设置

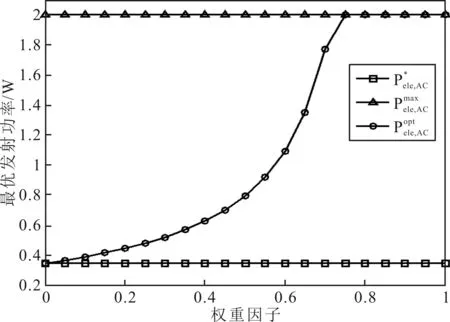
图3 最优发射功率随权重因子变化曲线

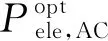
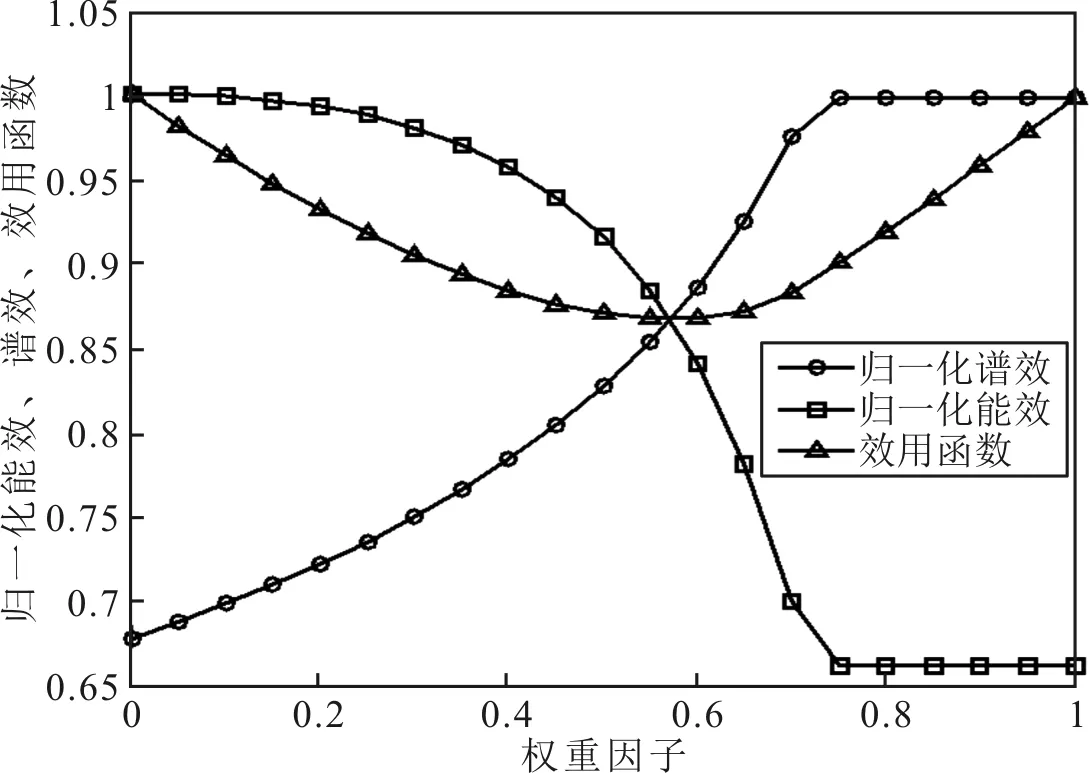
图4 归一化能、谱效以及效用函数与权重因子曲线

多目标优化下能谱效与权重因子的关系曲线图如图5所示。可以看出，整条曲线可以分为两部分。前一部分能效随谱效呈现单增趋势，即能效与谱效的变化趋势一致。后一部分能效随谱效呈现单减趋势，即能效与谱效的变化趋势相反。此外，从图5曲线中还可以看出权重因子ω=0对应的能效最大，但是谱效较小，且ω=0处刚好是整条曲线的拐点。权重因子ω=1时对应的谱效最大，但是能效较小。在ω=0到ω=1的中间的曲线部分代表权重因子兼顾了能效与谱效。在实际的应用场景中，需要根据实际情况需要来调节权重因子的大小从而满足对不同性能指标的需求。

图5 多目标优化下能谱效与权重因子的关系曲线

5 结语

引入比特功率加载技术推导出的闭合表达式，在此基础上，将谱效与能效两者制定为多目标优化问题，使用加权乘积标量法将两个目标优化函数降维至一个目标函数并证明单目标函数为拟凹函数，同时求解出最优发射功率。仿真结果表明，在最优发射功率时，通过调整权重因子可以实现能效与谱效优化的的兼顾。