罕遇地震作用下钢筋混凝土贮液池的抗震性能与加固研究*

毕继红 王光宇 王照耀 霍琳颖

1.天津大学建筑工程学院 300350

2.滨海土木工程结构与安全教育部重点实验室（天津大学） 300072

引言

贮液池是工业与民用建筑中常用的构筑物，在水利、石油、化工等领域有着广泛的应用［1］，对保证人们的正常生产生活至关重要。由于贮液池较多安置于人口密集的地区，在地震中一旦发生破坏将会造成严重的后果［2］，可能引发严重的次生灾害，对人们的生命和财产安全造成极大的危害。因此，贮液池的抗震性能也日益受到人们的重视。

对于贮液池的抗震问题，国内外许多学者做了大量的工作。Hoskins 等［3］研究了刚性储液池在模拟地震作用下的动水压力；Seeber 等［4］对基于柔性地基的三维弹性圆形贮液池进行分析，提出了结构在水平和竖直地震作用下的动力响应分析方法；Kianoush 等［5－7］考虑土-结构相互作用，对三维钢筋混凝土矩形贮液结构进行了动力时程分析，结果表明流体-储罐-土壤系统的动力响应对地震波的频率特性高度敏感；毕继红等［8］采用震度法和动力时程分析法对某半地下贮液池的抗震性能进行了分析，通过对比两种方法的分析结果，验证了震度法的可靠性。

本文在这些研究的基础上建立钢筋混凝土矩形贮液池的三维有限元模型，运用震度法计算结构在罕遇地震作用下的多工况弹性地震响应，通过能量守恒定则得到结构在弹塑性状态下的等效水平地震影响系数，并依据等效水平地震影响系数选择最不利工况，计算结构在该工况下的弹塑性地震响应。通过对贮液池结构的有限元分析，得出结构在罕遇地震下的最不利位置，并对其进行加固，为实际工程提供参考。

1 工程概况

本文中的贮液池建于1970 年，由净水池和设备间组成。净水池位于地面以下，在其中间有一块厚为0.8m的隔墙将净水池分为左右两部分，为方便叙述，将左侧部分定义为1 号池，右侧部分定义为2 号池。

1 号池尺寸为0.7m×20.8m×9.8m，顶板厚0.4m，底板厚1.0m，侧壁为上下变厚度墙壁，其上部为0.5m，下部为0.8m；在顶板和底板之间有16 根截面尺寸为0.7m×0.7m的柱A以及6片厚为0.2m的剪力墙；柱A 分为3 类，其中柱A2 和柱A3 为内部剪力墙的端柱，柱A1 未与剪力墙相连。2 号池尺寸为24.5m × 21.8m ×12.1m，顶板厚0.35m，侧壁厚0.7m，底板厚1.2m，顶板与底板之间有12 根截面尺寸为1.0m×1.0m的柱B 和1 根截面尺寸为1.2m ×1.2m的柱C。两池的最大水深均为8.25m，总有效容积为7900m3。设备间位于2 号池的上方，是突出地面的建筑，包括水泵室、换气室和电气室。贮液池的平、剖面如图1 所示。

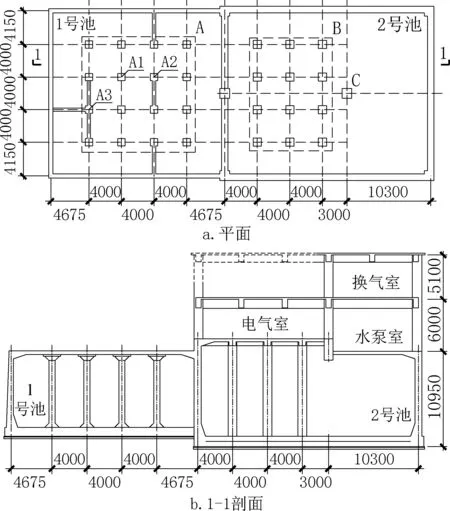
图1 贮液池平、剖面示意Fig.1 Plan and sectional view of reservoir

2 建立有限元模型

2.1 有限元模型

贮液池使用限元分析软件FINAL建立三维模型，如图2 所示，墙体采用板单元，梁柱采用梁单元。对于下部的净水池，考虑侧壁和顶板开孔的影响，对开孔处的局部网格进行了加密处理，同时考虑了钢筋和混凝土的非线性特性，其中钢筋通过定义构件截面的配筋率进行考虑，忽略钢筋与混凝土之间的滑移。对于上部的设备间，仅考虑其对下部净水池地震响应的影响，不考虑其材料非线性。

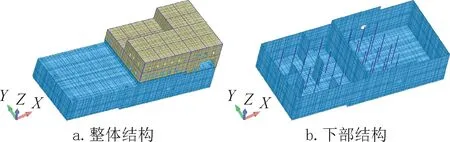
图2 有限元模型Fig.2 Finite element model

2.2 材料本构

1.钢筋本构关系

钢筋采用理想弹塑性模型［9］，用式（1）表示。

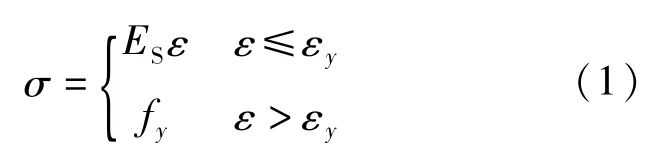
式中：σ为钢筋应力；ε 为钢筋应变；fy为钢筋屈服应力；εy为钢筋屈服应变，εy＝fy／Es；Es为钢筋弹性模量。

2.混凝土本构关系

混凝土受压时采用分段式曲线方程［10］，用式（2）～式（5）表示。

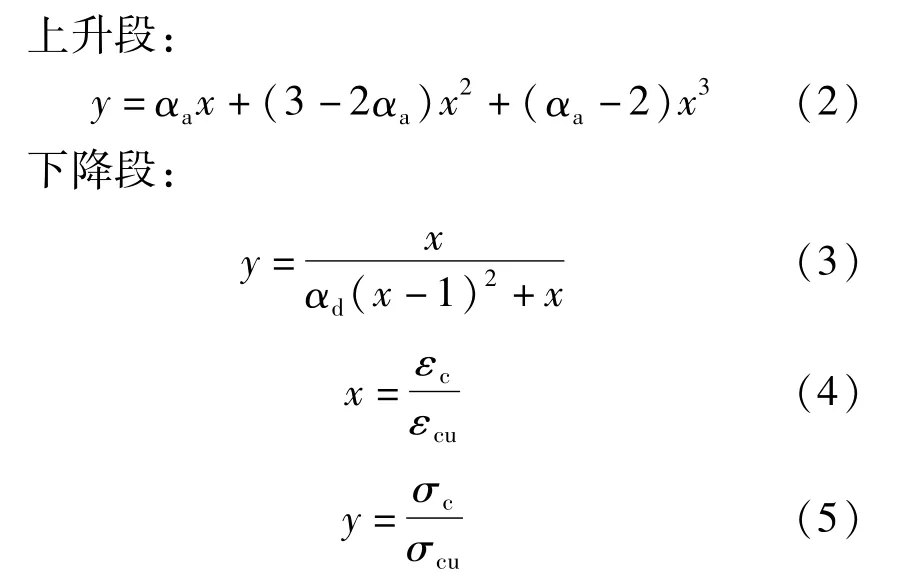
式中：αa为上升段参数，αa＝E0εcu／σcu，其中，E0为混凝土初始弹性模量；εcu为混凝土峰值压应变；σcu为混凝土实测抗压强度；αd为下降段参数，取2.0；εc为混凝土压应变；σc为混凝土压应力。

受拉时，在混凝土达到抗拉强度之前采用线弹性本构；开裂后考虑混凝土裂缝间的残余应力，采用断裂能模型［11］，如图3所示，用式（6）～式（8）表示。

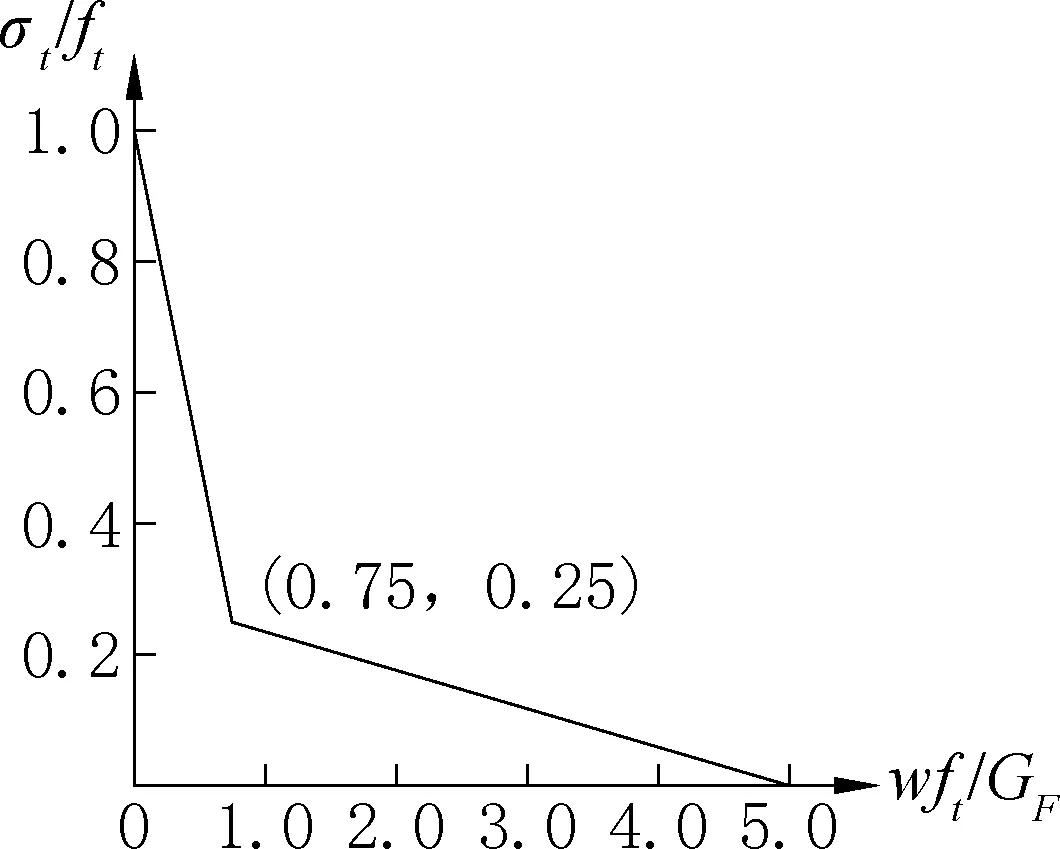
图3 断裂能模型Fig.3 Fracture energy model of concrete

式中：σt为混凝土拉应力；ft为混凝土实测抗拉强度；w为混凝土开裂宽度；GF为混凝土断裂能；d为混凝土中最大骨料粒径（mm）。

2.3 边界条件

土层的剖面情况如图4 所示（图中No.1～No.6 为地质勘测打孔位置）。贮液池周围土体主要是黏土层和碎石层，根据地质调查结果整理得到的地质参数如表1 所示。

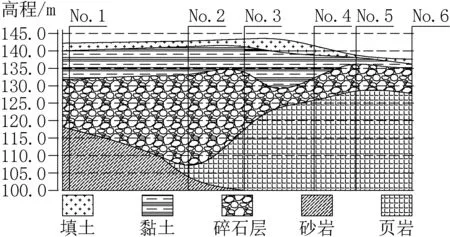
图4 土层断面示意Fig.4 Schematic diagram of soil section

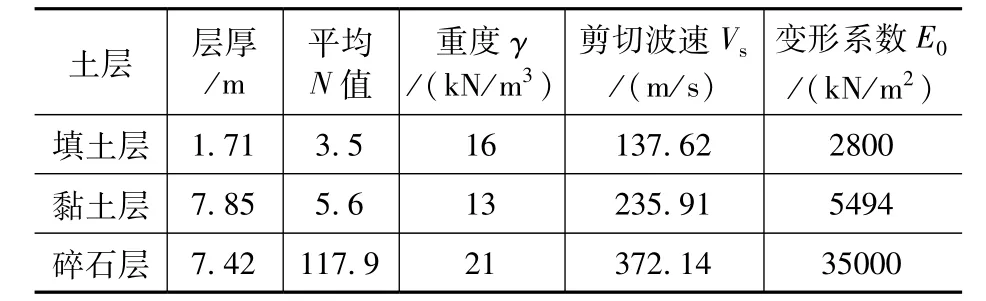
表1 土层参数Tab.1 Parameters of the soil layer

结构在地震作用下受到周围土体的约束，可以通过地基弹簧考虑土层与结构之间的相互作用。底板的地基反力系数可根据文献［12］提供的公式（9）、（10）进行计算。侧壁的地基反力系数与底板计算方法一致。

式中：E0为地基变形系数；α为地基承载力换算系数，地震时取8.0；Bv为基础底面等效宽度，当基础底面为矩形时，其中Av为基础底面面积。

地基弹簧使用八节点连接单元，通过定义连接单元的切向刚度和法向刚度来模拟土层对结构的约束作用。连接单元的切向和法向刚度即为地基弹簧切向和法向的反力系数。

2.4 地震动荷载

1.动水压力

文中贮液池内液体的质量与结构本身的质量相比较小，且池壁刚度较大，因此不考虑液体晃动对贮液池侧壁变形的影响。池壁所受动水压力沿水深呈抛物线分布［12］，用式（11）近似表示。

式中：P（z）为水深为z时的动水压；β 为贮液池宽深修正系数；γw为液体的重度；kh为水平地震影响系数；H为液体总深度。

2.主动土压力

地震时，地震动输入方向的池壁受到主动土压力的作用，计算池壁所受的主动土压力［12］如式（12）。

式中：PEA为深度为x时的主动土压；γ为土的重度；KEA为地震时的主动土压力系数，KEA＝0.24 ＋1.08kh；q为地表单位面积堆积荷载。

3 模态分析

考虑贮液池在使用阶段蓄水情况的变化，对1 号池和2 号池均处于最大水位状态（满水）、1 号池和2 号池均处于最小水位状态（空水）、1号池处于最大水位状态2 号池处于最小水位状态（1 满2 空）和1 号池处于最小水位状态2 号池处于最大水位状态（1 空2 满）四种情况进行模态分析。通过将贮液池所受的动水压力转化为附加质量来考虑池内液体对结构振动特性的影响。空水状态和满水状态的模态分析结果见表2 和表3。

由表2 和表3 可知，贮液池在满水和空水两种状态时，各阶模态的振型参与质量均较小，这是因为贮液池结构复杂，质量分布不集中所致；当处于满水状态时，贮液池质量最大，因此各阶模态的自振频率均较空水时小。满水时，结构第9 阶振型和第14 阶振型分别为Y向振型参与质量最大和X向振型参与质量最大，有效质量比分别为28.88%和16.02%，故满水时Y向结构自振周期取0.102s，X向结构自振周期取0.088s；空水时，结构第7 阶振型和第20 阶振型分别为Y向振型参与质量最大和X向振型参与质量最大，有效质量比分别为14.92%和17.00%，故空水时Y向结构自振周期取0.088s，X向结构自振周期取0.048s。满水和空水状态X向振动和Y向振动的主振型如图5 所示。

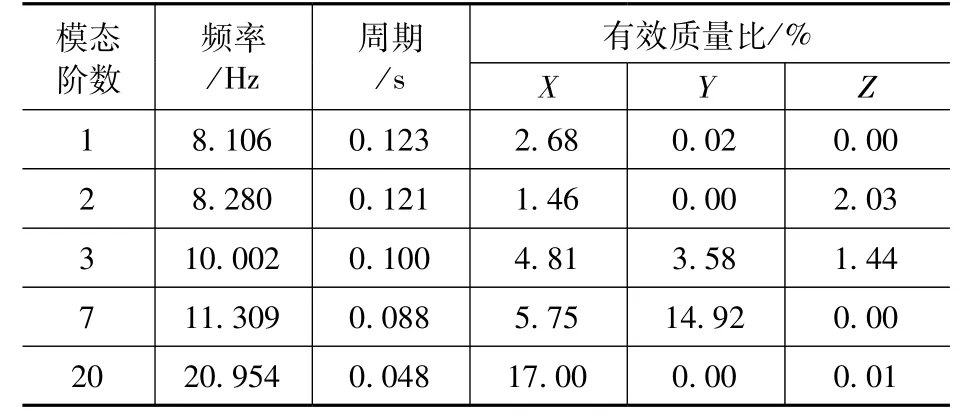
表2 空水模态分析结果Tab.2 Modal analysis results under empty water

表3 满水模态分析结果Tab.3 Modal analysis results under full water

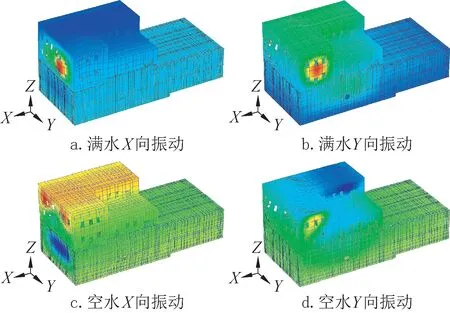
图5 贮液池主振型Fig.5 The main vibration shape of the reservoir

4 抗震性能分析

由于贮液池为非对称结构，本文考虑＋X、－X、＋Y和－Y四个不同的地震动输入方向，对贮液池处于满水、空水、1 空2 满和1 满2 空四种不同的蓄水状态进行了计算，并依据等效水平地震影响系数选择最不利的工况对结构进行非线性地震响应分析。

4.1 等效水平地震影响系数

震度法［12］是考虑结构的振动特征，将地震作用转化为等效静荷载，在弹性范围内对结构进行地震响应计算的抗震性能分析方法。采用震度法对结构进行弹性范围内的抗震分析时，首先需要确定结构在弹性状态下的水平地震影响系数kh。对于罕遇地震下的水平地震影响系数可由结构所在地区的设计水平加速度求得，如式（13）。

式中：kh为水平地震影响系数；a0为结构所在地罕遇地震下的设计水平加速度；g为重力加速度，取9.80m／s2。

本文中贮液池所在地的罕遇地震下的设计水平加速度为7.54m／s2，其罕遇地震下的水平地震影响系数为0.77。

由于震度法适用于结构在弹性范围内的地震响应分析，为了获得在罕遇地震下结构进入弹塑性状态后的地震响应，需要使用能量守恒定则确定结构在弹塑性状态下的等效水平地震影响系数k′h。能量守恒定则［12］是指具有弹塑性恢复力的单质点构筑物受到地震作用时，假设弹塑性响应和弹性响应两者的能量输入相同来获得结构的弹塑性响应的方法。

如图6 所示，O-C-A表示结构弹性响应时的kh-δ曲线，O-C-B-F 表示考虑结构弹塑性响应时的k′h-δ 曲线，其中δ 为结构在地震作用下的位移。当结构进入弹塑性域后，使S1和S2的面积相等，可以得到F点对应的等效水平地震影响系数k′h1，由此即可对结构进行弹塑性地震响应分析。根据能量守恒定则得到不同工况的等效水平地震影响系数k′h见表4。

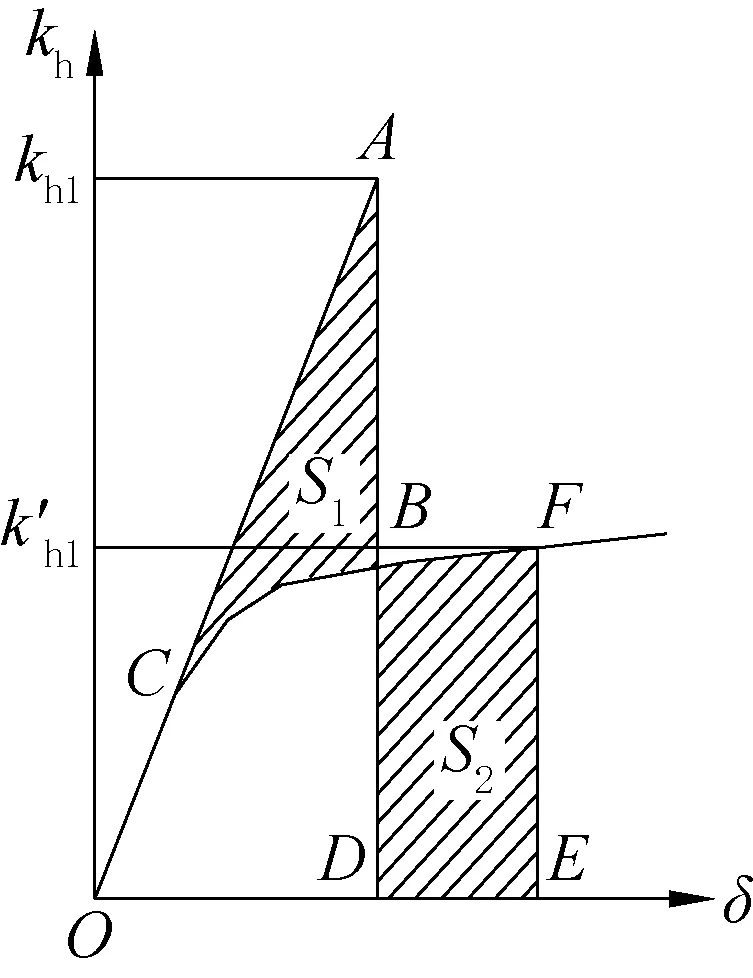
图6 能量守恒定则Fig.6 Law of conservation of energy

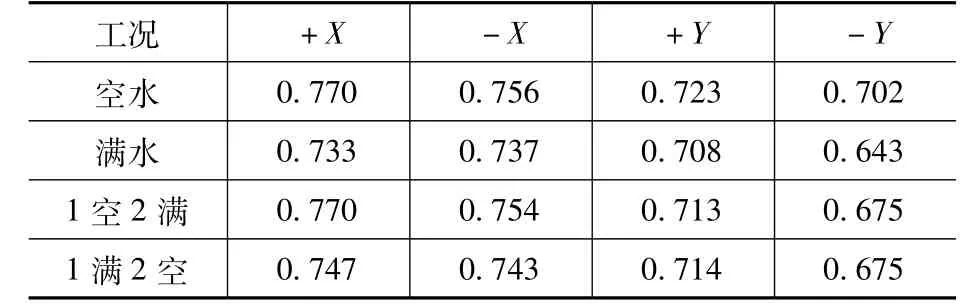
表4 等效水平地震影响系数Tab.4 Equivalent horizontal seismic influence coefficient

由表4 可知，当地震动输入方向为＋X时，蓄水状态为空水和1 空2 满的等效水平地震影响系数k′h为0.77，这与弹性状态的水平地震影响系数kh一致，说明此时结构未进入非线性状态；当地震动从Y向输入时，不同蓄水状态的k′h均较地震动由X向输入时小，这是由于结构在Y向的刚度小于X向刚度，且地震动由Y向输入时结构承受动水压和动土压的面积比地震动由X向输入时大，结构所受合力更大，非线性特性更显著，因此k′h也更小。

当贮液池处于满水状态时，不同地震动输入方向的k′h均为最小，说明满水状态为最不利的蓄水状态，之后将对处于满水状态时不同地震动输入方向的结构地震响应进行分析。

4.2 满水状态结构位移

贮液池在不同地震动输入方向的kh-δ 曲线如图7 所示。地震动由X向输入时，结构位移随水平地震影响系数的变化接近线性，＋X向输入时位移略大，为2.216mm；当地震动从Y向输入时，结构整体的位移较X向输入时大，这是因为结构Y向刚度较小的缘故，同时结构位移随水平地震影响系数的变化也显示出明显的非线性。由于结构的不对称，地震动由－Y向输入时结构的位移更大，为8.188mm，是＋Y向输入的1.793 倍。

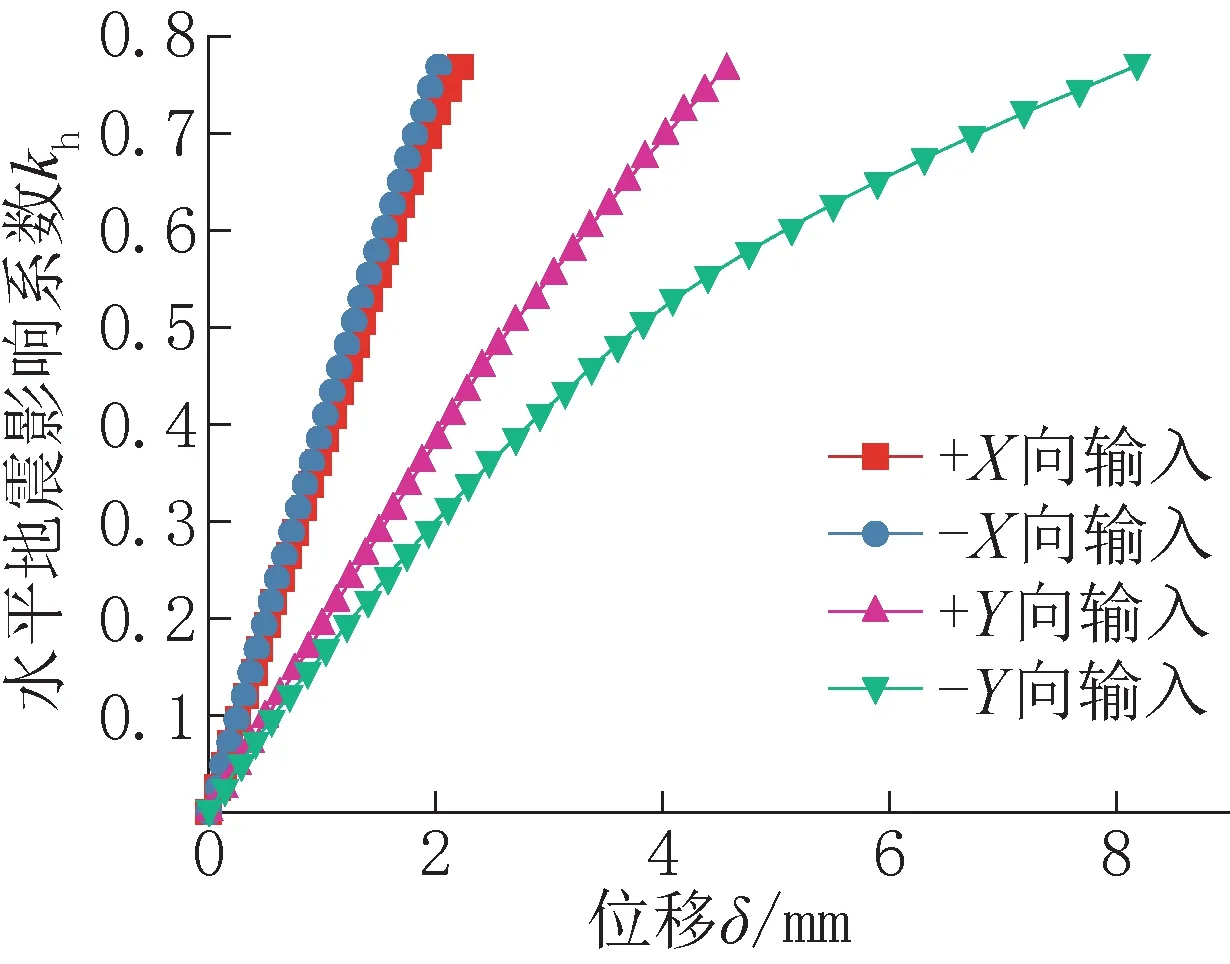
图7 不同工况下的kh-δ 曲线Fig.7 kh-δ curve under different working conditions

由上述分析可知，地震动由X向输入时，结构整体刚度下降不大，贮液池在X向有较强的抵抗强震的能力，而地震动由Y向输入时，结构整体刚度有明显的下降，尤其是从-Y向输入时，结构的kh-δ曲线已明显变缓。

4.3 墙板承载力校核

不同地震动输入方向时，贮液池下部结构X向和Y向钢筋的最大应力以及混凝土的最大压应变见表5。

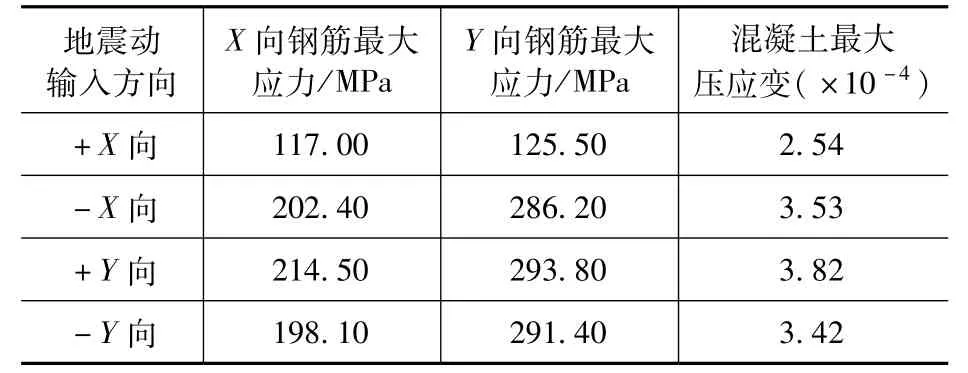
表5 墙板的承载力校核Tab.5 Capacity of shear wall bearing

由表5 可知，各工况下贮液池墙板中的钢筋在X向和Y向的最大拉应力均未达到屈服强度295MPa，同时混凝土的最大压应变为3.82 ×10－4，未达到极限压应变0.0033，墙板的承载力满足要求。

4.4 柱子承载力校核

由于结构的复杂性和不对称性，当地震动输入时，结构在X向和Y向均产生位移，这使得池内柱子处于双向受弯受剪的复杂受力状态。对于柱子的抗弯承载力，通过判断钢筋是否屈服和混凝土是否压碎进行校核，不同工况下柱内配筋的最大应力和混凝土最大压应变见表6 和表7。由表可知，柱子配筋的最大拉应力为294.5MPa，未达到屈服强度，同时混凝土的最大压应变为7.32 ×10－4，未超过极限压应变。

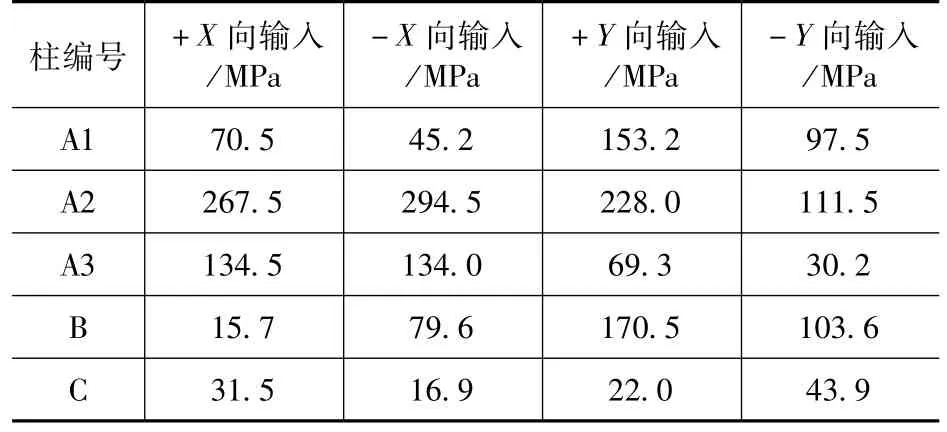
表6 各工况柱内配筋最大应力Tab.6 Stress of columns reinforcement under different working conditions

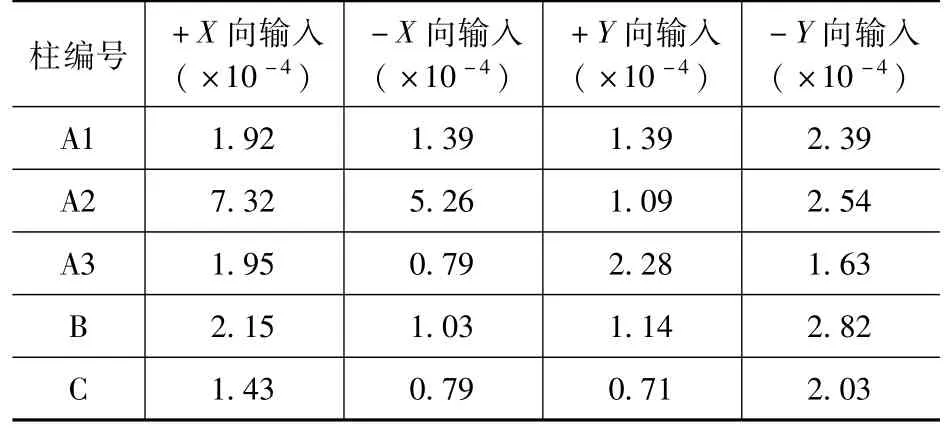
表7 各工况柱子混凝土最大压应变Tab.7 Maximum compressive strain of the concrete part of columns under different working conditions

对于柱子的抗剪承载力，分别考虑混凝土和钢筋的贡献［11］，计算截面的抗剪承载力，并与柱子剪力对比来判断是否发生剪切破坏。不同地震动输入方向下柱子截面的最大剪力如图8所示。

由图8 可知，柱A1、柱A3、柱B和柱C 在不同地震动输入方向下的最大剪力均未超过截面抗剪承载力；对于不同的地震动输入方向，柱A1、柱B、柱C的最大剪力变化不大，这是因为在不同地震动输入时，柱A1、柱B 和柱C 的剪力来自于两部分，一部分是由于承受动水压力和惯性力而引起，另一部分是由于地震作用造成柱子两端节点产生相对位移而引起，在不同地震动输入方向下，柱A1、柱B、柱C 承受的动水压力和惯性力的大小在数值上是相等的，而由地震作用引起的柱端相对位移略有差异，因此其剪力大小存在变化，但变化较小。

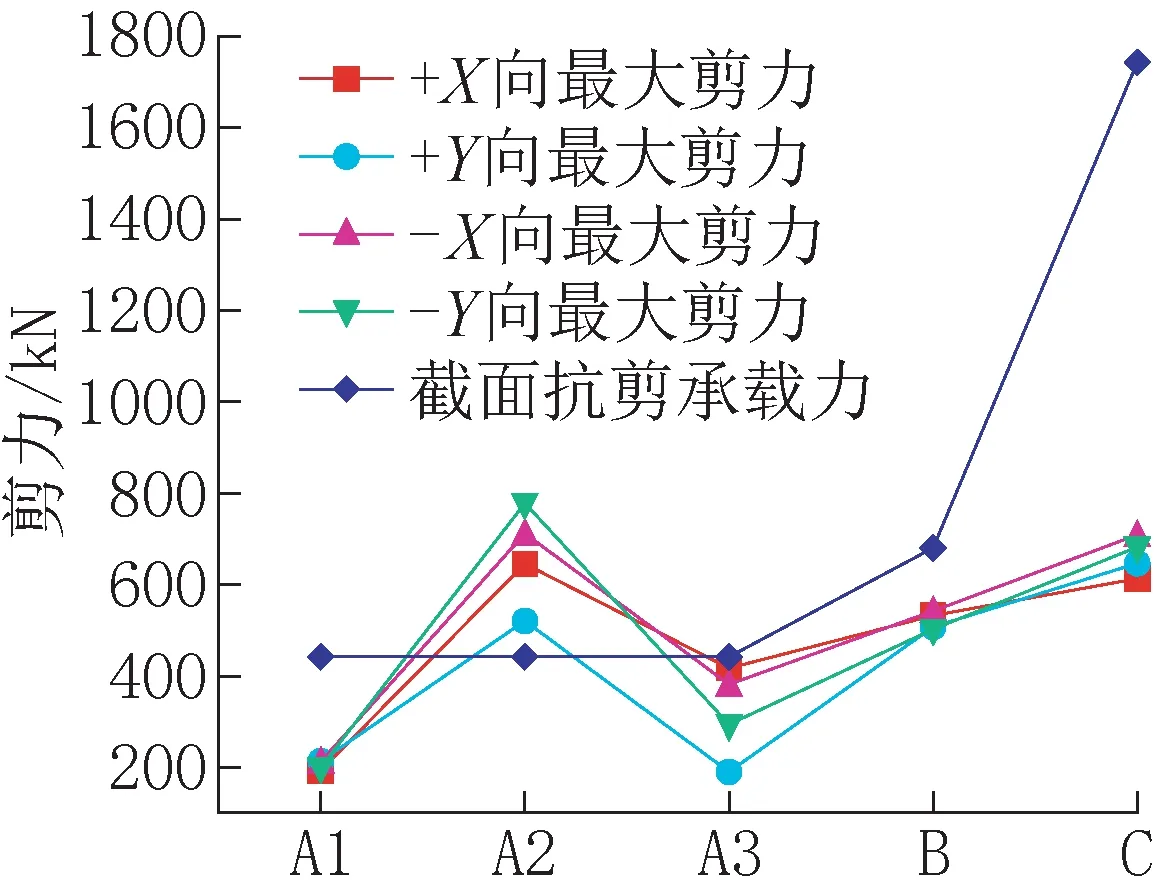
图8 不同工况柱子最大剪力Fig.8 Maximum shear force of column under different working conditions

在不同地震动输入方向下柱A2 最大剪力均超过了其截面的抗剪承载力，这是因为柱A2 和贮液池内部的剪力墙相连，当地震动由Y向输入时，贮液池侧壁因承受动土压力而产生较大变形，并通过内部剪力墙对柱A2 产生推挤作用，当地震动由X向输入时，内部剪力墙因承受动水压的面积较大而产生较大变形，对柱A2 产生拉扯作用，因此在不同工况下柱A2 均因抗剪承载力不足而发生剪切破坏。

5 抗震加固方法

由上述分析可知，当地震动由不同方向输入时，柱A2 的最大剪力均超出了其截面的抗剪承载力。由图8 可知，当地震动由－Y向输入时柱A2 的剪力最大，为779.6kN，超出其截面抗剪承载力77.1%，因此以该工况下柱A2 的抗剪承载力为补强的标准。

高延性混凝土（High Ductile Concrete，HDC）是一种具有高韧性、高抗裂性和高耐损伤能力的新型结构材料［13］，在拉伸和剪切作用下均表现出高延展性，采用HDC 材料加固可有效提高柱子的抗剪承载力。

HDC材料在单轴受拉时存在应变硬化现象［14］，假定其应力-应变曲线为双线性，用式（14）～式（16）表示。

为充分发挥HDC 材料的抗剪性能优势，本文采用沿柱高度四面围套的方式对柱A2 进行加固，加固前需对构件表面进行凿毛处理，以确保构件与加固层之间良好的粘结性能。分析时认为构件与加固层之间有良好的协同工作性能，不考虑两者表面之间的相互作用。

不同加固厚度下柱A2 的最大剪力和截面抗剪承载力如图9 所示。由图9 可知，随着加固厚度的增加，柱A2 的最大剪力也随之增加，这是因为柱A2 的刚度随加固层厚度的增大而增加，柱A2 的最大剪力也随之增加。当加固厚度为50mm时，柱A2 的最大剪力为1063.1kN，截面抗剪承载力为1100.7kN，两者相差3.42%，随着加固层厚度的继续增加，截面抗剪承载力与最大剪力的差值越来越大，当加固厚度达到60mm时，柱A2 的最大剪力为1164.3kN，截面抗剪承载力为1232.8kN，两者相差5.58%。由此可知，加固厚度为50mm 时，柱A2 的抗剪承载力即可满足要求，且随着加固厚度的继续增加，加固的经济效果随之下降。

图9 不同加固厚度补强结果Fig.9 Reinforcement results of different reinforcement thickness

6 结论

本文考虑不同地震动输入方向以及贮液池的不同蓄水状态，采用震度法对已建贮液池进行不同工况的抗震性能分析，得出以下结论：

1.贮液池不同蓄水状态下的地震响应差异较大。满水时结构整体质量较大，在地震作用下池壁所受动水压力也较大，结构的非线性特性显著；空水时，在地震作用下结构的非线性特性明显减弱。

2.不同地震动输入方向对结构的地震响应影响十分明显。由于结构的不对称，在满水状态下，地震动由＋X向和－X向输入时，结构的位移较小，且接近线性；当地震动由＋Y向和－Y向输入时，结构的位移较大，非线性特性显著。

3.贮液池内与剪力墙相连的柱A2 在地震作用下发生剪切破坏，采用HDC 面层加固可有效提高该柱的抗剪承载力。通过分析，当加固层厚度为50mm时，柱A2 的抗剪承载力可满足要求，随着加固层厚的继续增大，加固的经济效果随之下降。