风电机组中空夹层钢管混凝土塔筒钢板稳定性能研究*

王宇航 吕晰 王姝琪 周绪红 谭继可

1.重庆大学土木工程学院 400045

2.中国电力工程顾问集团西北电力设计院有限公司 西安710075

引言

为满足经济发展对能源的需求并改善环境污染问题，全球正在积极推进化石能源体系向低碳能源体系转型。在可再生能源中，风电能源凭借着成本较低的优势得到了广泛应用，风力发电技术也得到了大力发展。我国风电开发正向中东部和南部等低风速区迈进，为提高这些地区较差的风资源利用率，行业内领头企业着力于高塔架结构的研发推广。

目前，国内外风电场采用的风电机组塔架结构主要有钢结构塔架、钢筋混凝土结构塔架和钢-混凝土混合塔架，但这些形式的塔架结构在工程实践中都存在着一些不足之处［1－3］：钢结构塔架的制造和检修成本高且塔筒直径受限；钢筋混凝土塔架难以实现批量化生产；传统钢-混凝土混合塔架的分片混凝土塔段施工复杂、模板利用率低且现场装配耗时长。为适应机组大型化的发展趋势，开发出一种由上部钢塔筒和下部中空夹层钢管混凝土塔筒组成的新型混合塔架［4］。

中空夹层钢管混凝土塔筒为双钢板-混凝土组合结构，这一结构形式由Solomon 等人［5］于1976 年首次提出，其他研究人员后期又增设了栓钉、加劲肋等抗剪连接件以加强钢板和混凝土的协同工作性能［6］。目前，已有大量文献记载了双钢板-混凝土组合结构在轴压荷载下的受力性能研究，主要从理论分析、试验研究和数值模拟三个方面展开，研究发现影响该受力体系抗压承载力的主要因素有核心混凝土材料［7，8］、钢板屈服强度［9－11］、含钢率［12］、钢板厚度［13，14］以及连接件［12－15］的类型、尺寸、间距和布置方式等，其中距厚比［7－11，15－19］（栓钉竖向间距与钢板厚度之比）是影响钢板稳定的关键因素，得到了国内外学者的广泛关注。现有研究主要存在两方面的不足：一是仅考虑了钢板和混凝土共同加载下组合结构的整体受压性能，缺少对组合结构中的钢板单独加压时稳定性能的研究；二是研究对象中的内、外钢板均为平板。因此，本文研究了混合塔筒中钢板单独承受轴压荷载时的失稳性能，混凝土仅对钢板起面外支撑作用，分析了钢板曲率半径、钢板屈服强度、钢板厚度、距厚比等因素的影响，以期为推进新型混合塔架在风电行业中的应用提供理论依据。

1 新型混合塔筒

基于边缘加劲组合壳体的中空夹层钢管混凝土新型混合塔筒［4］如图1 所示，上部为钢塔筒，下部为中空夹层钢管混凝土塔筒（传统混合塔架下部常采用钢筋混凝土塔筒），两者之间采用高强螺栓法兰连接。下部塔筒由各片边缘加劲组合壳体通过高强螺栓沿环向拼接而成，单片组合结构由焊有栓钉的内、外钢板和核心混凝土组成。

图1 新型混合塔筒Fig.1 New type of hybrid tower

塔筒是风电机组结构组成中最重要的承载构件，需要支撑所有上部结构重量，同时还要承受塔顶传递来的复杂荷载和横向风荷载作用［3］。对于中空夹层钢管混凝土塔筒来说，复合荷载作用下压应力最大区域出现在机组背风面塔筒底部，当压应力足够大时可能发生钢板局部失稳，导致塔筒在组合截面达到极限承载力之前破坏。

2 试验概况

2.1 试件设计

试验选取了整圆中空夹层钢管混凝土塔筒中的一片进行缩尺试件的设计，试件由内、外钢板，上、下端板和核心混凝土、栓钉组成，其尺寸见图2。试件高度、宽度均为1000mm，内钢板曲率半径和外钢板曲率半径分别为1000mm和1100mm，钢板厚度为2.3mm，内钢板栓钉环向间距和外钢板栓钉环向间距分别为147mm 和161mm，栓钉竖向间距为150mm。为施加均匀作用的轴向荷载，试件上、下端焊接12mm 厚的端板，并在上端板处焊接加劲肋以避免发生局部失稳破坏。为实现仅在钢板施加轴向载荷并去除混凝土对钢板稳定性能的影响，浇筑混凝土前采取了以下措施：在钢板内表面粘贴一层聚四氟乙烯膜，在试件底部和每相邻两排栓钉间各铺设一层珍珠棉。

图2 试件示意（单位：mm）Fig.2 Schematic diagram of specimen（unit：mm）

根据文献［20］，实测核心混凝土的标准立方体抗压强度平均值为37.3MPa。根据文献［21］，钢板选用了强度等级为Q235 的钢材，实测力学性能见表1。

表1 钢板材性试验结果Tab.1 Material properties of steel

2.2 加载装置及加载制度

试验采用YAW-5000 微机控制电液伺服压力试验机，加载装置如图3 所示。由于组合构件截面形心与上下端板截面形心重合，因此加载时只需将下端板形心与加载装置下承载板形心对中，即可实现轴向荷载的施加。

图3 试验加载装置Fig.3 Test setup

图4 位移计布置Fig.4 Arrangement of LVDT

在试件底部向上进行单调轴压加载，首先以10%的试件名义承载力（fyAs）大小的压力进行预加载以确保试件均匀受力且位移计正常工作，完成预加载后采用位移控制加载，加载速率为0.2mm／min，加载至位移达到9mm（0.01 倍试件有效高度）或试件严重变形时，停止试验。

2.3 量测方案

本次试验主要量测试件承受的轴向压力和发生的轴向位移。其中，轴向荷载由加载装置上的力传感器记录；内、外钢板中心位置对称布置LVDT 位移计，如图4 所示，用于测量试件轴向位移。

3 试验结果及分析

以面向内钢板时的左右方位为基准命名试件的左侧板和右侧板，如图5 所示，以便描述试件破坏过程。

图5 钢板的命名方式Fig.5 Naming of steel plates

试验准确测量了试件在整个加载过程中的荷载-位移曲线（图6），并对试验现象进行了实时记录。加载初期，荷载-位移曲线基本呈线性上升，试件表面没有明显变形，弹性段在曲线上升段的占比较大；当加载至0.77mm 时荷载达801kN，在内钢板第二行栓钉的第一个间距处试件发生鼓曲，荷载-位移曲线斜率开始减小；随加载进行内、外钢板各部位依次发生鼓曲，钢板刚度逐渐减小；加载至1.15mm时达到峰值荷载955kN。此后荷载-位移曲线进入下降段，随加载位移增大内、外钢板各部位继续发生鼓曲并逐渐贯通；加载至4.72mm时荷载下降到665kN，内、外钢板的鼓曲在右侧板处完全贯通，试验结束。试件最终破坏形态如图7 所示，可以看出内、外钢板均呈现出栓钉间局部失稳的破坏模式。

图6 试件荷载-位移曲线Fig.6 Load-displacement curve of specimen

图7 试件最终破坏形态Fig.7 Final failure mode of specimen

4 有限元模型

4.1 模型建立

本文采用ABAQUS 软件对双钢板-混凝土塔筒试件在轴向压力作用下的受力过程进行了数值模拟分析。有限元模型中的钢板采用四节点减缩积分薄壳单元S4R进行模拟，厚度方向采用五个积分点的Simpson 积分；混凝土采用八节点缩减积分三维实体单元C3D8R 进行模拟；栓钉采用抗拉刚度无穷大的线弹性弹簧模拟。由于本文研究重点在于钢板的局部稳定性能，不考虑钢板和混凝土的粘结作用以及栓钉的抗剪作用，故仅对钢板与混凝土之间的界面关系采用“面-面接触”模拟，法向设为“硬”接触（Hard contact），切向设为无摩擦接触（Frictionless）。试验过程中端板未出现变形，因此模型中未建端板，而是直接将试件顶部钢板与混凝土表面设置为固定端约束，将试件底部钢板截面与其形心下方参考点RP-1进行运动耦合（Kinematic），限制参考点侧向位移并向上施加竖向位移，从而模拟试验的加载条件。试件有限元模型的网格划分、边界条件与加载方式如图8 所示。

图8 有限元模型Fig.8 Finite element

4.2 单元选取和材料模型

有限元建模时，混凝土选用八节点缩减积分三维实体单元C3D8R，钢板选用四节点缩减积分薄壳单元S4R 且厚度方向采用5 个积分点的Simpson积分，栓钉采用抗拉刚度为无穷大的线弹性弹簧（spring）进行简化模拟。混凝土材料的应力-应变模型定义为线弹性模型，弹性模量取32500N／mm2，泊松比取0.2。钢板钢材的应力-应变模型定义为理想弹塑性模型，屈服强度和弹性模量采用实测值。

4.3 初始缺陷

有限元模型主要考虑两种初始缺陷的影响：初始面外几何缺陷和荷载初偏心。为了考虑初始面外几何缺陷的影响，需要先将钢板的实测初始面外几何缺陷施加在有限元模型具有代表性的点上，在完成静力分析后得到试件的初始面外几何缺陷分布，将其引入模型。荷载初偏心则可直接通过调整加载点RP-1 相对底部钢板截面形心的位置，将实测值引入模型。

5 有限元模型验证

5.1 破坏模式

试验得到了中空夹层钢管混凝土塔筒试件的内、外钢板局部失稳破坏模式：外钢板顶部第一行栓钉与第二行栓钉之间出现贯通鼓曲，内钢板在第二行栓钉上方邻近位置出现贯通鼓曲。为验证有限元模型的正确性，将完成轴压加载的模拟结果与试验结果进行对比，如图9 所示，可以看出有限元模拟结果中内、外钢板也是出现栓钉间的局部失稳破坏，即在顶部两行栓钉之间出现贯通鼓曲，且模型失稳位置和试验结果也比较相符。对比结果表明，本文建立的有限元模型能够较为准确地模拟出试件的整体破坏模式。

图9 试验和模拟结果的破坏模式对比Fig.9 Comparison of failure modes between test and simulation

5.2 荷载-位移曲线

将试验和有限元模拟得到的荷载-位移曲线绘制在图10中，可以看出两曲线在弹性阶段基本吻合，说明模型可以较为准确地模拟试件初始刚度。

图10 试验和模拟的荷载-位移曲线对比Fig.10 Comparison of load-displacement curves between test and simulation

有限元模拟得到的荷载-位移曲线先后出现两个峰值点，主要是由于有限元模型中采用线弹性弹簧模拟栓钉，并在钢板与混凝土之间设置无摩擦接触，能够更为理想地消除栓钉的抗剪作用以及混凝土和钢板的组合作用。试验中钢板的局部失稳始终发生在试件同一高度截面，鼓曲逐渐贯通。而在理想化有限元模拟条件下，钢板失稳出现的位置较为随机，随着加载的进行内钢板出现一处局部失稳，导致曲线在达到第一个峰值点后骤降；继续加载，钢板在另一高度截面逐渐发生贯通屈曲，使得曲线出现了第二个峰值点。

试验得到的峰值承载力为955.25kN，有限元模拟得到的峰值承载力为945.25kN，误差在1%左右，进一步验证了有限元模型能够较好地模拟试件中钢板在轴向压力作用下的稳定性能。为参数化分析提供可靠依据。

6 参数分析

在试验和数值模拟结果对比研究的基础上，定义初始参数值，建立了用于分析中空夹层钢管混凝土塔筒中钢板峰值强度的有限元模型。每组模型单独变化一个参数展开模拟，以钢板平均应变与钢板高度的比值δv／H为横坐标，钢板平均应力与钢材屈服强度的比值σv／fy为纵坐标，绘制各组模型归一化的平均应力-应变曲线。分析得到了钢板曲率半径、钢板屈服强度、钢板厚度和栓钉竖向间距对中空夹层钢管混凝土塔筒中钢板在轴压荷载下承载能力的影响规律，对比各参数的敏感性，为确定中空夹层钢管混凝土塔筒构件的关键设计参数和设计指标提供参考。

6.1 钢板曲率半径

建立钢板曲率半径R分别为400mm、600mm、800mm和1000mm 的一组有限元模型。图11 给出了模拟得到的不同钢板曲率半径下内、外钢板归一化的平均应力-应变关系曲线，发现内钢板的峰值强度和归一化的平均应力-应变关系曲线在弹性阶段的刚度均大于外钢板。

由图11 可以看出，曲率半径对内、外钢板的影响规律基本一致：随着钢板曲率半径的减小，钢板的峰值强度不断提高，这是由于钢板曲率半径越小，混凝土对钢板的支撑作用越强；但钢板曲率半径的改变不会影响归一化曲线在弹性阶段的刚度。

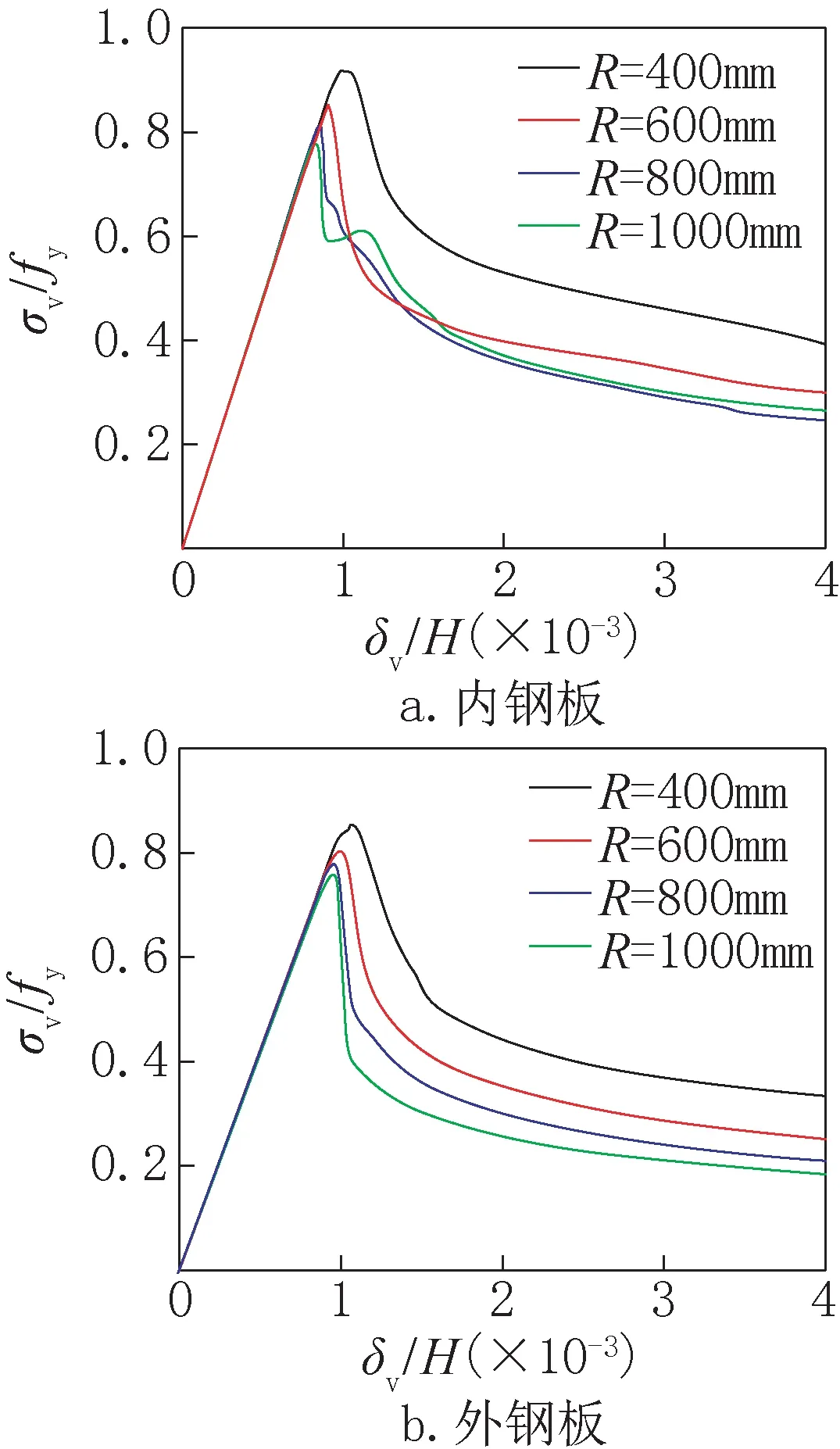
图11 钢板曲率半径对钢板峰值强度的影响Fig.11 Effect of steel plate curvature radius on the peak strength of steel plate

6.2 钢板屈服强度

建立了钢板屈服强度fy分别为235MPa、345MPa、390MPa和420MPa 的一组有限元模型。图12 给出了模拟得到的不同钢板屈服强度下内、外钢板归一化的平均应力-应变关系曲线，发现内钢板的峰值强度和归一化的平均应力-应变关系曲线在弹性阶段的刚度均大于外钢板。

由图12 可以看出，钢板屈服强度对内、外钢板的影响规律基本一致：随着钢板屈服强度的增大钢板的峰值强度呈现出下降的趋势，达到390MPa后钢板屈服强度对钢板峰值强度的影响程度较小；归一化曲线在弹性阶段的刚度也随着钢板屈服强度的增大而减小。钢板发生屈曲时的应力并未达到钢材屈服强度，且板件弹性屈曲应力与材料强度无关，因此对钢板平均应力进行归一化后，钢板在弹性阶段的刚度和峰值强度随钢板屈曲强度的增大而减小。

图12 钢板屈服强度对钢板峰值强度的影响Fig.12 Effect of steel plate yield strength on the peak strength of steel plate

6.3 钢板厚度

建立钢板厚度t分别为1mm、2mm、3mm、4mm和5mm的一组有限元模型。图13 给出了模拟得到的不同钢板厚度下内、外钢板归一化的平均应力-应变关系曲线，发现内钢板的峰值强度和归一化的平均应力-应变关系曲线在弹性阶段的刚度均大于外钢板。

由图13 可以看出，钢板厚度对内、外钢板的影响规律基本一致：归一化曲线在弹性阶段的刚度随着钢板厚度的增大略有增大；钢板的峰值强度随着钢板厚度的增大而大幅提高，在钢板厚度由1mm增大到2mm时峰值强度的提高程度最为显著，这是由于增大钢板厚度能够直接减小板件宽厚比，从而有效提高板件的弹性屈曲应力。

图13 钢板厚度对钢板峰值强度的影响Fig.13 Effect of steel plate thickness on the peak strength of steel plate

6.4 栓钉竖向间距

建立栓钉竖向间距Sv分别为100mm、200mm、300mm、400mm 和600mm 的一组有限元模型，并建立了不设置栓钉的模型作为对照组。图14给出了模拟得到的不同栓钉竖向间距下内、外钢板归一化的平均应力-应变关系曲线，发现内钢板的峰值强度和归一化的平均应力-应变关系曲线在弹性阶段的刚度均大于外钢板。

图14 栓钉竖向间距对钢板峰值强度的影响Fig.14 Effect of stud vertical spacing on the peak strength of steel plate

由图14 可以看出，栓钉竖向间距对内、外钢板的影响规律基本一致：随着栓钉竖向间距的减小，钢板的峰值强度不断提高；归一化曲线在弹性阶段的刚度也随着栓钉竖向间距的减小而增大。原因在于布置栓钉可以将钢板划分为小区格，随着栓钉竖向间距的减小，区格内钢板的宽厚比相应减小，从而提高了钢板的弹性屈服应力。

通过有限元模拟得到四组模型内、外钢板的归一化平均应力-应变关系曲线，分析结果表明：钢板曲率半径、钢板屈服强度、钢板厚度和栓钉竖向间距等参数对中空夹层钢管混凝土塔筒中内钢板在轴压荷载下承载能力的影响规律与对外钢板的影响规律基本一致；曲线在弹性阶段的刚度对钢板屈服强度和栓钉竖向间距两个参数较为敏感；而钢板峰值强度对钢板厚度这一参数最为敏感。后续对于新型混合塔筒设计方法的研究可在以上影响因素分析的基础上展开。

7 结论

1.风电机组中空夹层钢管混凝土塔筒试件中钢板在轴压荷载作用下，内、外钢板的破坏模式均为两行栓钉间的局部失稳破坏，从荷载-位移曲线可将破坏过程大致划分为三个阶段。

2.中空夹层钢管混凝土塔筒试件有限元分析得到的破坏形态与试验结果基本一致，荷载-位移曲线与试验曲线吻合较好，验证了有限元数值模拟结果的准确性和可靠性。

3.中空夹层钢管混凝土塔筒试件中核心混凝土对内、外钢板提供平面外支撑，内钢板的局部稳定性能优于外钢板的局部稳定性能，具体体现在内钢板峰值强度以及归一化平均应力-应变曲线在弹性阶段的刚度均大于外钢板。

4.有限元参数分析结果表明：内、外钢板在轴压荷载作用下的峰值强度随钢板曲率半径的减小、钢板屈服强度的降低、钢板厚度的增大、栓钉竖向间距的减小而增大；归一化的平均应力-应变曲线在弹性阶段的刚度随钢板厚度的增大、钢板屈服强度的减小、栓钉竖向间距的减小而呈现出增大的趋势，而钢板曲率半径对其影响甚微。