长距离水平定向钻回拖力的预测及分析

单彬彬 曹守金 李明

1.中国市政工程中南设计研究总院有限公司 武汉430000

2.中国建筑一局（集团）有限公司 北京100000

引言

水平定向钻进技术广泛应用于石油天然气、电力、通信、给水、排水、煤气、热力等地下管线的铺设，以其对环境、城市交通的最小影响和危害，及其效率和成本等优势，日益受到人们的重视，取得了很好的社会效益和经济效益［1］。

管道回拖是水平定向钻进技术中重要的一环，回拖力预测可为穿越工程设计、钻机型号选择、管道在施工中的稳定性评价、回拖减阻工艺制定等关键环节提供依据，受到大量学者的关注［2－6］。

现有规范中尽管给出了回拖力的计算公式，但参数取值范围较大，公式预测值与实测值有很大偏差，原因之一是未充分考虑回拖力的组成。本文在总结已有研究成果的基础上，充分考虑回拖力的组成，提出新的回拖力计算公式，并用实际工程案例进行验证。

1 回拖力计算

现有规范或规程中回拖力的计算公式大致可分为三类，一是适用于钢管管材，二是适用于聚乙烯管材，三是未作明确适用于何种管材，分类见表1。

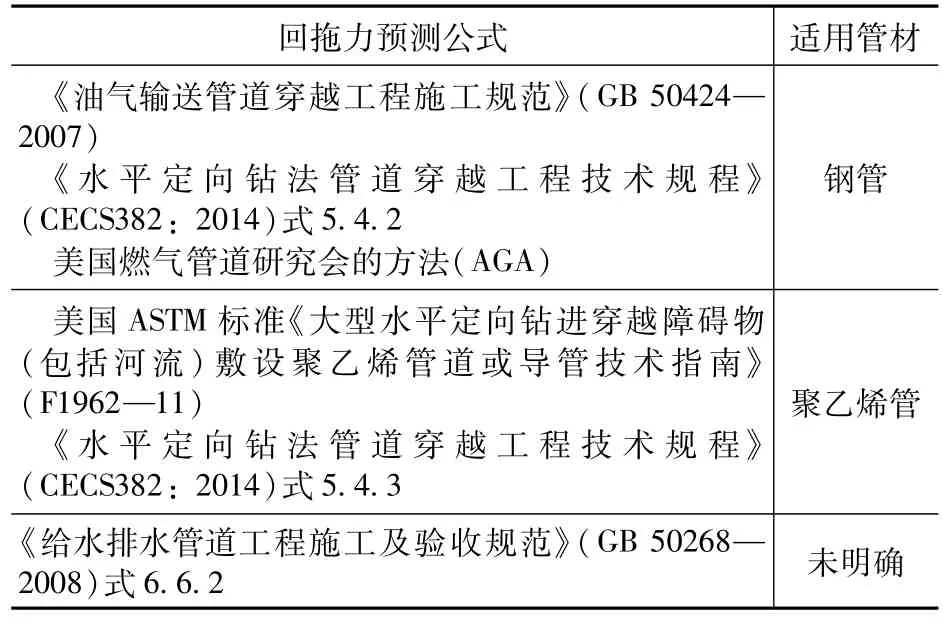
表1 回拖力预测公式分类Tab.1 Classification of Drag Force prediction formula

本文选取4 个国内外权威机构或国家标准所提供的回拖力计算方法，并以实际工程的统计数据为基础，将计算结果与实际所测回拖力进行比较分析，供工程设计人员参考。

1.1 CECS382：2014

当敷设管道为钢管时，回拖力按下式计算：

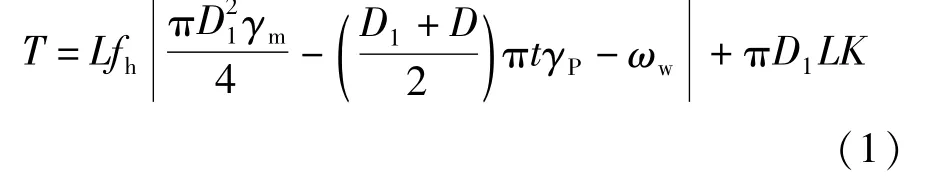
式中：L为穿越长度，m；D为管道内径，m；t为管道壁厚，m；D1为管道外径，m；fh为钢管与孔壁之间摩擦系数，0.1～0.3；K为泥浆粘滞系数，0.15～0.35，kPa；γm为泥浆重度，kN／m3；γP为钢材重度，kN／m3；ωw为单位长度配重，kN／m。

规范中认为管道在地面摩阻力是可控的，管道回拖阻力主要包括管道静浮力引起的摩阻力和泥浆的黏滞阻力。计算公式中的钢管与孔壁的摩擦系数及泥浆粘滞系数的变动范围较宽，回拖力的计算结果受主观影响较大且范围太宽。公式未考虑弯曲变形阻力、管道与地面的摩阻力。

1.2 GB 50424—2007

该规范适用于油气输送管道在陆上穿越人工或天然障碍的新建和扩建工程。其回拖力计算公式主要考虑了穿越管道与孔壁之间的摩擦阻力和泥浆对管道的黏阻力。其计算公式与CECS382：2014 中公式相同，只是建议参数取值不同，GB 50424—2007 中建议管道在充满泥浆的孔中的摩擦系数取0.3，泥浆粘滞系数取0.175。

1.3 美国燃气管道研究会的计算方法（AGA）

AGA计算方法是由Huey 等人在1996 年为定向钻安装钢管道而提出的，公式如下：

（1）直线段拉力的计算公式为：

式中：T1为直线段拉力，kN；Ff为孔道内摩擦阻力，kN；FDR为孔液的阻力，kN；μb为管道与孔壁的摩擦系数；WP为考虑钻孔液浮力后管道单位长度的净重，kN／m；L为直线段管道长度，m；β为管道倾角；μmud为泥浆粘滞系数，kPa。

（2）弯曲段拉力的计算公式为：

式中：T2为弯曲段拉力，kN；Larc为弯曲段管道长度，m；N为弯曲段管土相互作用的法向力，kN，需迭代求解。

（3）总的回拖力为：

式中：Ti为第i段管道上的轴向拉力，kN；T为总的轴向拉力，kN。

公式考虑了管土的摩擦阻力、泥浆的黏阻力和弯曲变形阻力的影响，但没有考虑管道拖入孔道之前与地表面的摩擦阻力，并认为管道进入钻孔时的回拖力为零，其最大回拖力出现在回拖最后阶段并以递增的方法沿管道分布。因此此法把整个管道分解为许多直线段和曲线段，最后的轴向拉力为每小段拉力的总和。

1.4 ASTM技术指南

美国材料试验协会（ASTM）制定的F1962-11，指导和帮助工程师更好地理解定向钻进铺设聚乙烯管道的技术细节。其中回拖力计算公式如下：

式中：TA、TB、TC、TD为A、B、C、D 四点的回拖力，kN；L1、L2、L3、L4为管道额外增加长度、AB、BC、CD段长度，m；va为管道与地面摩擦系数；vb为管道与孔道壁摩擦系数；ωa为管道每延米自重，kN／m；ωb为管道每延米净浮力，kN／m；H为管道埋深，m；α 为管道入土角，弧度；β为管道出土角，弧度；Td为泥浆拖拽力，kN；ΔP为计算处泥浆压力差，kPa；Aa为管道与钻孔壁间圆环截面积，m2。

公式考虑了管道与地面的摩擦阻力、管道与钻孔的摩擦阻力、绞盘效应、泥浆拖拽力的影响。CECS382：2014 式5.4.3 即参考ASTM 规范，但规程中未考虑泥浆拖拽力Td。

2 回拖力组成分析

钻孔清孔过程中，钻机回拖力监测仪表始终处于较高的数值，320kN～400kN，钻杆与扩孔器产生的阻力不可忽略不计。以上述规范规程中已有预测公式为基础，结合工程中回拖力实测数据分析，回拖力组成包括管道与地面的摩擦阻力、管道与孔壁的摩擦阻力、钻孔液对管道产生的阻力、钻杆与孔壁的摩擦阻力、扩孔器与孔壁的摩擦阻力、钻孔液对扩孔器产生的阻力及弯曲变形阻力（绞盘效应）。分述如下：

（1）管道与地面摩擦阻力：

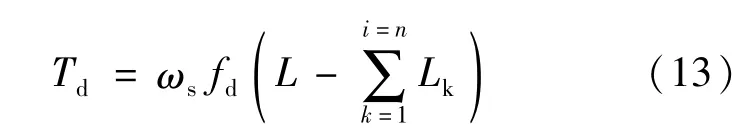
式中：Td为管道与地面摩擦阻力，kN；ωs为单位长度管道的重力，kN／m；fd为管道与地面的摩擦系数；L为管道的总长度，m；Lk为管道在孔道内的长度，m。

（2）孔道内摩擦阻力：

式中：Tb为管道与地面摩擦阻力，kN；ωb为孔道内单位长度管道的浮力，kN／m；fb为管道与孔道壁的摩擦系数；αk为孔道与水平向的倾斜角；管道重力的分量方向与拉力方向相同时取负号。

（3）孔道内钻孔液的阻力

钻孔内的液体流动有一个屈服点，当压力差大于屈服点时，液体才可以流动。

式中：Tv为钻孔液阻力，kN；C为作用管道上的钻孔液阻力分项系数；P1为管道牵引点位置处泥浆压力，kPa；P2为地面处泥浆压力，kPa；Dp、Dd为管道、钻杆直径，m；Aa为管道与钻孔壁间圆环截面积，m2。

（4）钻杆及扩孔器阻力

回拖过程中，钻杆、扩孔器和管道为相连接的整体。现有规范中公式仅考虑管道牵引点处的拉力，未计入钻杆、扩孔器产生的阻力。钻杆阻力计算类似管道阻力计算，但应注意钻孔内钻液流动方向会有一个分界点，在管道牵引点处，液体往管道侧流向地面，另一侧则相反。由于钻杆侧钻液流动方向与钻杆运动方向相同，假设两者速度相同，则钻杆上不产生钻孔液阻力。

扩孔器阻力：

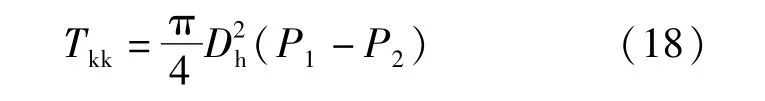
式中：Tkk为扩孔器阻力，kN；Dh为钻孔直径，m。

钻杆阻力：

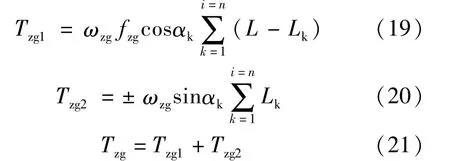
式中：Tzg为钻杆阻力，kN；ωzg为孔道内单位长度钻杆的净浮力，kN／m；fzg为钻杆与孔道壁的摩擦系数；钻杆重力的分量方向与拉力方向相同时取负号。

（5）管道弯曲变形阻力

管道通过弯曲段时，由于管道的变形和拉力方向的改变，使弯曲段出口的拉力大于弯曲段进口的拉力，其拉力计算的公式与简化的力学模型有关，其中包括绞盘效应和弯曲效应，假定钻孔平顺，此处只考虑绞盘效应。

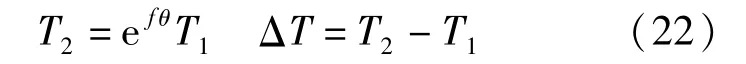
式中：T1、T2为弯曲段进口、出口拉力，kN；f为管道与地面或孔道壁摩擦系数；θ 为管道弯曲段夹角，弧度。

则总的阻力为：

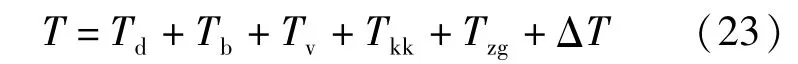
3 工程案例

3.1 概况

某输水管线工程，保证供水安全，采用双线输水，管道公称管径DN600，设计压力1.1MPa。受规划限制，两条管道上下敷设，水平间距2.43m，竖向间距6m，由南至北穿越新盖房分洪道，单线管道长度分别为1955m、2006m。

设计选用螺旋缝焊接钢管，材质Q345，壁厚14mm。钢管外防腐采用熔融结合环氧粉末涂层，涂层为加强级。设计出土角及入土角均取10°，入土角和出土角处为弧形段，曲率半径900m；中间段为水平段，管道穿越土层主要分别为粉土、粉质黏土层，管道顶设计标高距离现状河床分别为16m 和22m。扩孔分三级：550mm、750mm、950mm；管道“二接一”，场地限制分两段预制：1126m、880m，先回拖1126m段，后焊接880m段再二次回拖。

3.2 回拖力预测分析

本文将设备仪表实测值与规范、规程及本文方法预测值对比分析，计算参数及回拖力对比分别见表2、图1。

表2 回拖力计算参数Tab.2 Pullback calculation parameters

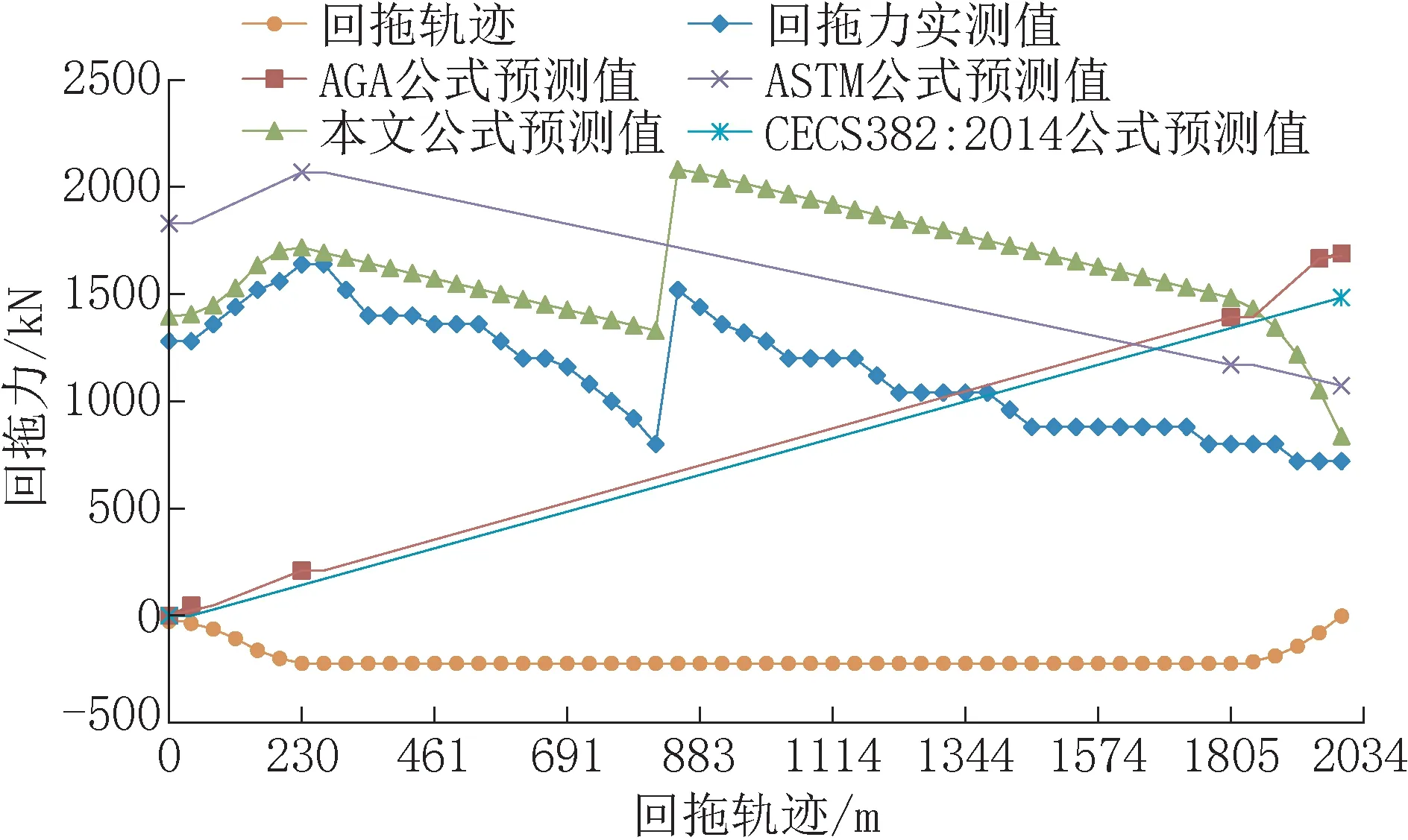
图1 回拖力与回拖轨迹的关系Fig.1 Relationship between pullback force and the pullback track

由图1 回拖力实测值可以看出，回拖力先增大至1640kN，后呈递减趋势，在“二接一”处，回拖力突变增加至1520kN，后呈递减趋势，逐渐减小至720kN，由此可见回拖力并非简单的呈递增趋势，最大值出现在管道入土侧弯曲段终点，这是因为孔外管道摩阻力大于孔内摩阻力及弯曲段绞盘效应导致的；AGA公式预测值呈递增趋势，在弯曲段，由于管道弯曲阻力的存在，回拖力增加幅度较大，最大回拖力预测值为1689.8kN；CECS382：2014 预测值呈线性增加，最大回拖力预测值为1484kN；ASTM公式预测值呈先增大后减小趋势，预测最大值为2069kN，大体趋势与实测值一致，但公式无法预测“二接一”工况；本文公式预测值规律与实测值一致，回拖力呈先增大后减少趋势，并在“二接一”处回拖力突变，最大预测值为2082.4kN，出现在“二接一”节点。

4 结论

1.回拖力最大值出现在管道入土侧弯曲段终点，回拖力呈先增大后减少趋势。当孔外管道未采取减阻措施时，应考虑孔外管道与地面的摩阻力。

2.管道弯曲段阻力增大幅度较大，回拖力预测应考虑弯曲段的绞盘效应。

3.在清孔过程中，钻机回拖力监测值一直维持在较大数值，回拖力预测中，不可忽略钻杆与扩孔器产生的阻力。

4.ASTM公式预测值与实测值规律大体一致，但未考虑钻杆及扩孔器阻力，且也不适用于“二接一”回拖工况。

5.CECS382：2014 中公式未考虑孔外管道摩擦阻力、弯曲段绞盘效应、钻杆与扩孔器产生的阻力，预测值偏小。

6.AGA公式预测值呈递增趋势，在弯曲段，由于管道弯曲阻力的存在，回拖力增加幅度较大，与实测值变化规律相差较大，但最大预测值与最大实测值相近。

7.本文预测方法与实测值规律一致，预测值精确度满足工程要求，可为管段采用“二接一”布置的工程提供参考。