输电塔交叉斜材承载力试验及有限元分析

屈可明 李正良 黄祖林

1.重庆大学土木工程学院 400045

2.山地城镇建设与新技术教育部重点实验室（重庆大学） 400045

引言

交叉斜材是保证输电塔稳定性的重要构件，是输电塔抵抗横向荷载的关键构件，其力学性能研究具有重要意义。实际工程中，输电塔结构因为存在构造间隙出现连接节点螺栓滑移的现象。螺栓滑移会影响交叉斜材的力学特性，国内外相关规范定义钢结构节点连接强度的计算公式时却未考虑节点连接滑移的影响，有可能产生安全隐患或浪费现象。对此，孙冬明［1］将螺栓滑移试验实测的力-位移曲线引入到MATLAB 程序用于输电塔结构的变形计算，引入了一个系数η来表征滑移杆件线刚度的折减，得到了更接近实际的结果。Jiang W.Q.等人［2］完成了全尺寸输电塔试验，并模拟研究了不同滑移模型对输电塔受力变形特性的影响。黄伟东［3］等建立了输电塔螺栓搭接结构的三维有限元模型，通过数值模拟及与已有试验结果的对比，分析了影响滑移曲线的因素。杨风利［4］建立了典型输电塔结构部分塔体的有限元模型来考虑螺栓滑移的影响，发现螺栓滑移对主材轴向力和加载点附近的水平节点挠度有很大的影响。李正良［5］等人对不等边角钢交叉斜材进行了试验研究，并利用ABAQUS有限元研究了不同内力比、钢材强度、截面规格对斜材承载力的影响，提出了不等边角钢交叉斜材计算长度修正系数。

目前有关交叉斜材的研究以理论分析和数值模拟为主，已有的试验研究存在对真实受力状态模拟不充分和年代久远等问题。此外，部分学者虽然深入研究了不同工况下螺栓滑移对输电塔结构的影响，但缺乏一个统一的计算模型，针对交叉斜材中螺栓滑移产生的力学性能影响的研究较少。因此，相关的试验研究及数值模拟亟待展开。

本文以工程中常用的输电塔交叉斜材节间为研究对象，建立全尺寸试验模型，进行交叉斜材的稳定性试验研究，探究交叉斜材在不同拉压比工况下的承载能力。采用ANSYS 有限元软件模拟真实条件下的螺栓连接节点的滑移模型，用已知试验数据验证其正确性，得到螺栓连接节点的位移-荷载曲线。基于得到的位移-荷载曲线，建立交叉斜材节间的滑移模型，进行交叉斜材的有限元分析。对比交叉斜材试验结果，验证交叉斜材滑移模型是否准确，并进行试验未涉及的参数分析。

1 输电塔交叉斜材试验研究

1.1 试验方案

1.试验概况

试验选取典型的交叉斜材节间作为基本研究对象，探究交叉斜材节间在不同拉压比工况下的承载能力。交叉斜材采用Q355 钢材，节间构造见图1，单独的两根交叉斜材组成仅斜材节间，增加辅材到辅材节间，对比两种节间极限承载力随拉压比变化的趋势。考虑到仅斜材节间缺少面内约束，弯曲屈曲绕弱轴发生，回转半径为1.58cm，而辅材节间由于辅材为斜材提供了足够的面内约束，其屈曲绕平行轴发生，回转半径为2.46cm。为保证两种节间名义长细比相同，将辅材节间尺寸扩大至1.57倍。在两斜材指定拉压比的条件下，对试验材施加单调分级荷载直至其破坏，记录节间极限承载力。

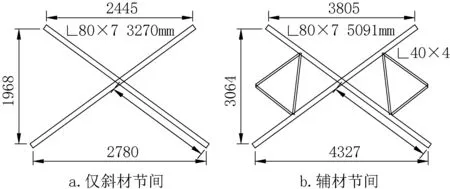
图1 节间构造（单位：mm）Fig.1 Structure of the tower section（unit：mm）

节间采用对称布置，设置不同的拉压比工况如表1 所示。实际工程中，输电塔会受到如风荷载、地震作用、拉索荷载等横向荷载作用，这些荷载主要由交叉斜材承担。由于横向荷载的方向是随机的，故交叉斜材的内力比在－1～1 之间变化，这与试验工况设置是一致的。杆件端部约束设置为单颗螺栓连接，斜材通过螺栓直接连接到加载端，辅材通过螺栓连接到斜材。由于螺栓与螺孔之间不可避免的装配间隙和螺孔承压面的挤压变形，结构在荷载作用下，连接面的滑移是不可避免的。限于试验条件，螺栓滑移未能在试验中测量，后文将采用数值模拟研究滑移变形对斜材稳定性的影响。

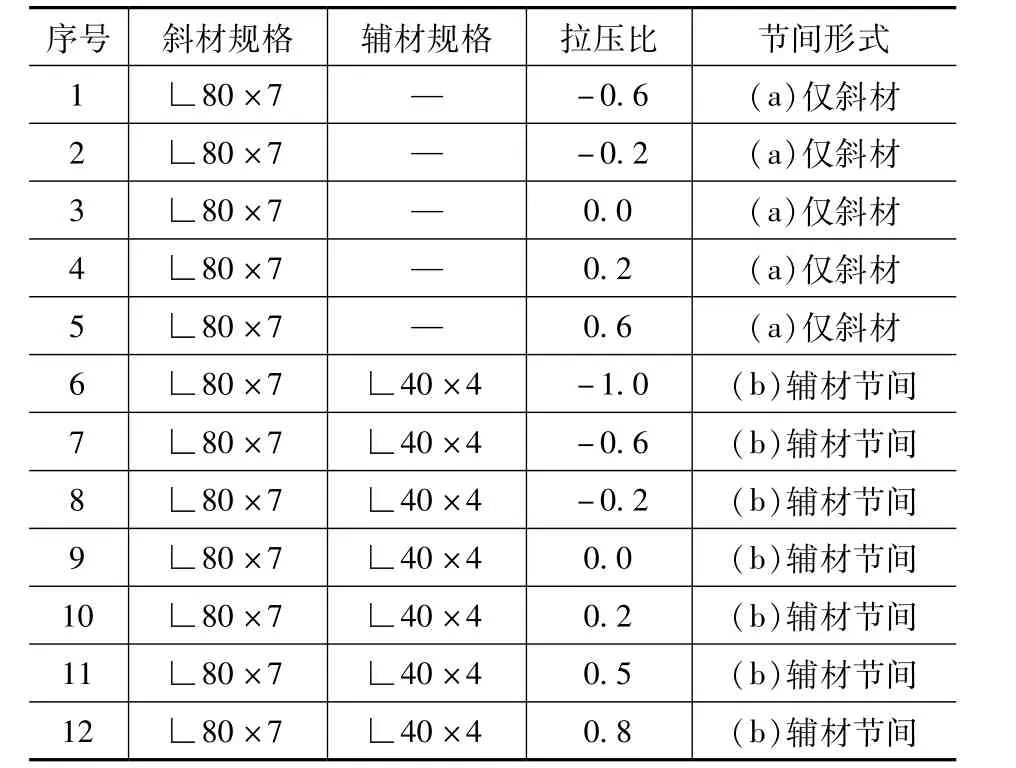
表1 节间试验工况设置Tab.1 The settings of the test structure in different stress ratios

2.加载方案

节间试验在平衡框中完成，由四根大截面箱型钢梁连成，具有足够大的刚度，框架内实现静力自平衡。采用正立位试验，双向千斤顶斜向安装，通过紧固螺栓固接于上横梁，两种平面节间形式采用相同的加载装置。测力传感器安装在千斤顶的缸头上，实时读取斜材中的内力值。辅材节间试验布置如图2 所示。

图2 辅材节间试验布置Fig.2 Pictures of the X-braced bars

正式加载前首先进行预加载，校验各仪器仪表正常工作状态。正式加载的每一加载级以力控制，达到指定加载级后持荷1min，然后采集数据，直至荷载越过峰值有较大降低，或节间出现较大变形，停止加载。为获得交叉斜材节间更多的受力特性及其变形特征，试验过程中还需要测量角钢试件的截面应变分布、平面外位移变化、轴向压缩及拉伸变形。

3.测点布置

仅斜材节间的每根斜材被交叉点分成两段，每段中点和交叉点处设置测量点，测量应变和平面外位移。角钢两肢均测量应变，应变片贴于肢中心处。辅材节间的斜材被辅助材再次分割，在每段跨中截面设置应变片，每根斜材共计8 个应变片。在与仅斜材节间相同的位置设置位移计用于测量平面外位移，两斜材上共计5 个面外位移计。所有辅材均取跨中截面为应变测量点，不进行位移测量，辅材共计12 个应变片。对于所有节间，斜材的轴向变形通过设置在千斤顶的位移计测量的出缸量来表达。位移及应变测量点布置如图3 所示。

图3 试验测点布置Fig.3 Layout of the testing points

4.材性试验

本试验采用的钢材为Q355 高强度钢，其名义屈服强度为355MPa。材性试验在重庆大学岩土馆的INSTRON材料试验1342 系统上进行，材性试验结果见表2。

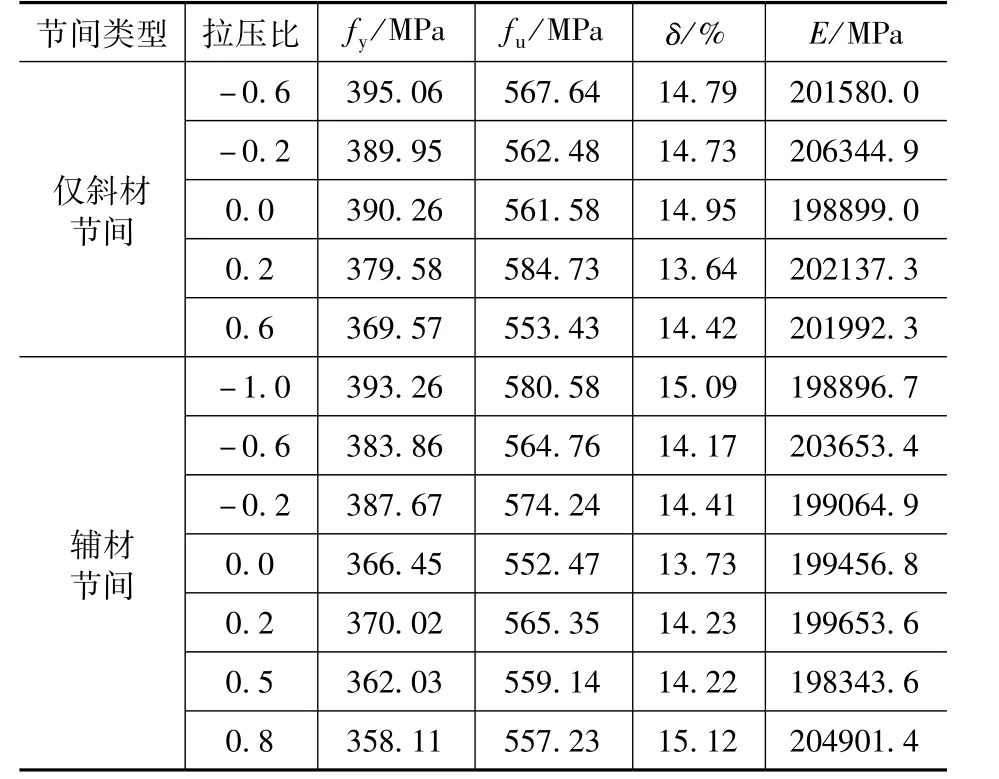
表2 材性试验结果Tab.2 Tensile test results

1.2 试验结果分析

1.节间破坏模式

仅斜材节间的试验完成了5 个不同拉压比工况，每个拉压比有3 组对照试验。辅材节间的试验完成了7 个不同拉压比工况，每个拉压比有3组对照试验。本文将一拉一压工况下的压杆和同时受压工况下压力较大的压杆统称为压杆，另外一杆为拉杆。

仅斜材节间都是压杆的长段发生屈曲破坏，如图4 所示，屈服位置都从压杆长段的中间开始。拉压比会决定屈曲破坏模式，当拉压比≤－0.2 时，压杆绕最小轴失稳，其他情况都为绕平行轴失稳，如图5 所示。

图4 仅斜材的压杆长段屈曲Fig.4 Buckling of the simple cross bars

图5 压杆失稳破坏Fig.5 Buckling of compression bars

辅材节间存在压杆长段屈曲和压杆整体屈曲两种模式，如图6 所示。当拉压比≤－0.2 时，压杆长段绕连接肢平行轴屈曲；拉压比＞－0.2时，压杆整体绕连接肢平行轴屈曲，交叉点变形加大，压杆长段的变形仍较为明显。对于辅材节间其屈曲全绕平行轴展开，可见辅助材确实增强了交叉斜材的整体稳定性。压杆失稳时可以看到S型失稳模式，且拉压比越小这个S 型趋势越明显，这与目前的理论研究比较吻合。

图6 辅材节间的屈曲模式Fig.6 The buckling mode of the complicated cross bars

2.极限承载力分析

将试验所得的极限承载力整理分析，并与《架空输电线路杆塔结构技术规定》（DL／T 5154—2012）［6］（下称《架空规范》）和《钢结构设计标准》（GB 50017—2017）［7］（下称《钢规》）计算结果进行初步对比分析。取每种工况三次对比试验极限承载力的平均值作为试验结果，使用材性试验值进行理论计算。表3给出了试验研究结果汇总。

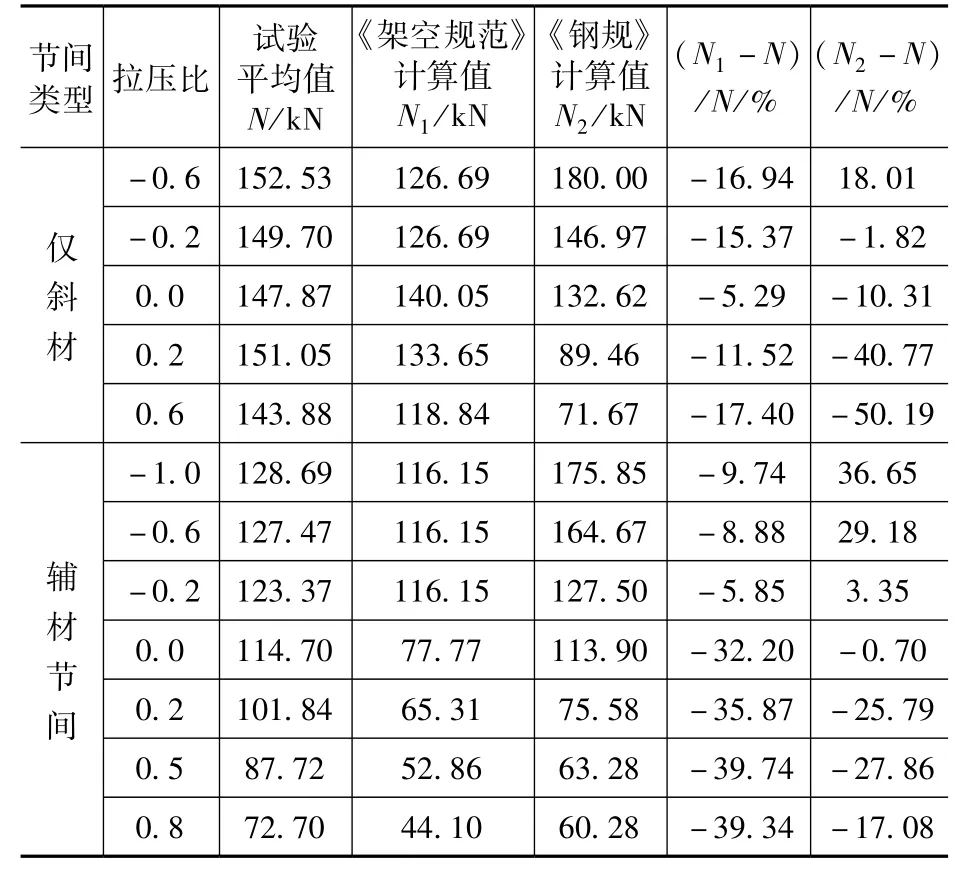
表3 交叉斜材承载力值与规范计算结果对比Tab.3 Comparison of the experimental results with the codes’

总体看来，试验极限承载力随拉压比的增大而减小，随着拉杆由受拉转为受压，其对压杆的约束减弱，从而使压杆更早发生失稳。仅斜材节间的试验值变化不大，最大值与最小值仅相差6%，可知拉杆受力对压杆破坏影响不大。破坏都是从压杆长段展开，而《钢规》从整体失稳去修正的计算方法考虑不够精细。对于辅材节间，《钢规》计算值在拉压比≤－0.2 时差异很大，此时破坏是在压杆长段展开，《钢规》按全长计算的思想不适用这种情况。

《架空规范》计算仅斜材节间的交叉斜材承载力较为接近计算值，两者差异小于20%。对辅材节间一拉一压工况时《架空规范》较准确，但同时受压工况下差异很大。对于辅材节间两端同时受压工况，由试验结果可知拉杆仍可以为压杆提供一定支撑，而《架空规范》在计算承载力时，计算长度由1.1 倍压杆长段长度变为考虑拉压比修正的全长长度，故差异较大。

3.荷载-位移分析

根据交叉斜材试验数据，绘制压杆所受荷载与压杆轴向位移的关系曲线，如图7 所示。

图7 荷载-轴向位移曲线Fig.7 The load-axial displacement curve

对于仅斜材节间的荷载-轴向位移曲线，不同拉压比工况下曲线路径基本类似，说明仅斜材节间的破坏模式与两斜材的拉压情况关系不大。而辅材节间的荷载-轴向位移曲线在不同拉压比工况下形状有较大区别，说明辅材节间的破坏模式随拉压情况变化。

交叉斜材节间破坏往往发生在压杆长段和斜材交叉点，将轴向荷载和交叉点、压杆下测点的面外位移分别绘制如图8所示的曲线。需说明的是，曲线竖直向下是因为位移超过了位移计的最大量程。

如图8a、b所示，交叉点的面外刚度随拉压比变化而变化。对于仅斜材节间，在达到最大稳定承载力之前交叉点的面外刚度相差不大，说明达到稳定承载力前结构的受力模式类似。在结构达到最大承载力后交叉点的刚度随拉压比增大而减小，这时拉杆对压杆的支撑作用显现出来。对于辅材节间，轴向荷载较小时拉压比对结构面外刚度的影响不大。当荷载逐渐接近稳定承载力时，拉压比越大，拉杆提供的支撑越小，交叉点的面外刚度就越小，且变化幅度远大于仅斜材节间，再次说明拉压比影响辅材节间的破坏模式。

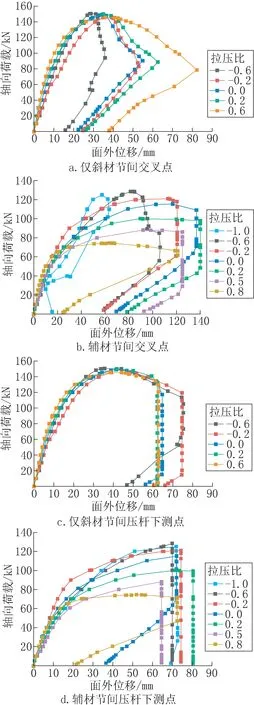
图8 荷载-侧向位移曲线Fig.8 The load-lateral displacement curve of the joint

如图8c、d所示，拉压比大小对仅斜材节间的关键点面外刚度影响不大。对于辅材节间，当拉压比≤－0.2 时关键点的面外刚度基本不变，当拉压比＞－0.2 时关键点的面外刚度随拉压比的增大而减小。

4.荷载-应变分析

交叉斜材不同拉压比工况下，压杆下测点连接肢与非连接肢的应变随轴向荷载变化的荷载-应变曲线，如图9 所示。

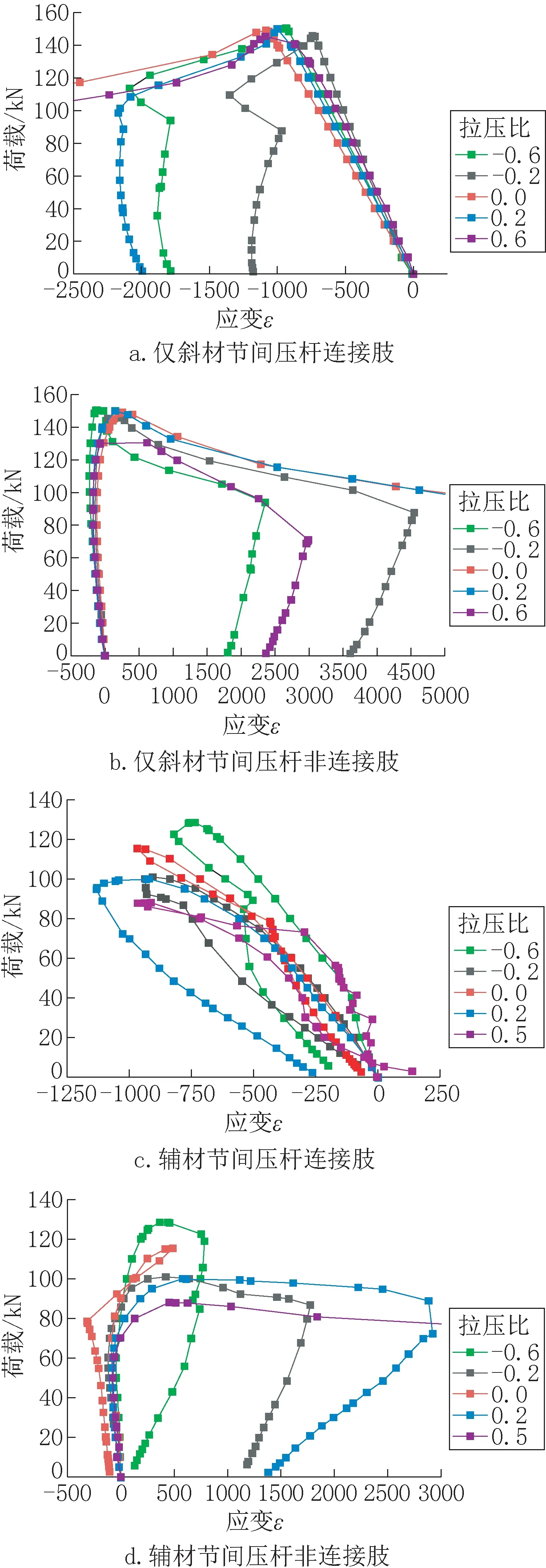
图9 压杆下测点荷载-应变曲线Fig.9 The load-strain curve of the lower test points of compression bars

如图9a、b所示，仅斜材节间连接肢与非连接肢的变形不同，应变关系也有所不同。连接肢受轴向荷载产生压应变，应变线性增长，达到极限承载力变快速增加。非连接肢的应变在荷载较小时产生弹性压应变，随着荷载的增大，压杆下测点已经开始产生弯曲，弯曲产生的拉应变逐渐抵消压应变，但两个应变值都较小。压杆达到极限承载力后，非连接肢受向外凸的拉应力，应变快速增加。值得注意的是，不同拉压比工况下，其荷载-应变曲线无明显差别，故拉压比对结构破坏点的应变影响不大，且连接肢与非连接肢受力情况有所不同。

图9c、d分别展示了辅材节间不同拉压比工况下压杆下测点连接肢与非连接肢的荷载-应变曲线，对比图9a、b可知辅材节间受力情况更为复杂，主要原因是其破坏形式更多样，不全是压杆下测点破坏。另外，不同拉压比辅材节间的下测点连接肢在荷载开始时应变不呈线性增长且在结构失稳时应变没有突增，这是由于辅助材的支撑作用使结构一开始受力更均匀，荷载不会直接全部传递给压杆。

2 考虑螺栓滑移的输电塔交叉斜材有限元分析

2.1 螺栓节点滑移的有限元分析

1.有限元模型建立

根据王朋［8］2014年的螺栓连接节点试验结果，采用ANSYS有限元软件建立螺栓节点滑移模型。模型中角钢构件采用Q345 钢，螺栓采用6.8 级M16，孔径为17.5mm，即配合间隙取1.5mm。

钢材选取ANSYS 软件中的理想弹塑性模型的本构关系，满足Von Mises 屈服准则。其弹性模量为2.1 ×105MPa，泊松比为0.3。角钢采用SOLID185 单元，螺栓采用SOLID187 单元，便于加密区网格划分。螺杆表面与角钢内螺孔的接触面定义为“自动闭合接触”，其余接触面定义为“标准接触”，接触算法为“罚函数法”，法向接触刚度系数FKN 取0.8，切向刚度系数FKT 取0.2，螺栓的摩擦系数取0.3。螺栓节点滑移模型如图10 所示。

图10 螺栓节点滑移模型Fig.10 Slip model of bolted joints

在螺栓中建立预紧截面并施加预紧力，预紧力取25kN。将其中一片角钢的端部设置为固定约束，限制所有自由度，另一片角钢端部施加匀速增加的位移以模拟试验中的位移荷载，求解过程考虑了非线性。计算分成了多个荷载步，先设置分析步施加一个小的螺栓荷载来消除角钢板的刚体约束，再设置单独的分析步施加螺栓预紧力，准确地模拟真实的螺栓连接关系。

2.有限元模型验证

由于试验会不可避免地产生安装偏差，而有限元分析中采用的理想间隙，故必须消除安装偏差的影响后才能进行有限元模型的验证。周星［9］将安装偏差分成了4 个分量，发现这4 个分量只对滑移距离有不同程度的影响，他提出了单个螺栓连接的修正公式以考虑安装偏差的影响。本文将王朋［8］试验得到的荷载-位移曲线根据近似公式计算得到4 个偏移量，重新代入有限元模拟得到新的修正后的荷载-位移曲线，再将其与试验结果进行了比较。

王朋［8］完成了多个构件规格的螺栓连接节点试验，选取一颗螺栓构件和两颗螺栓构件的试验结果进行验证，每组试验含4组对照试验。根据试件规格进行模拟，得到模拟结果与试验结果的荷载-位移曲线见图11。

如图11a 所示，预设的配合间隙为1.5mm，而试验构件的滑移距离从1.60mm 到2.30mm 变化，其平均滑移距离为1.98mm，经过修正后的模拟结果能更好地与试验值吻合。修正后的滑移荷载、滑移前线刚度、滑移距离、滑移后线刚度都与试验值符合很好。试验的极限承载力略大于修正后的模拟值，这是因为模拟中杆件的屈服强度小于真实屈服强度，该误差可在进行材性试验后消除。

如图11b所示，两颗螺栓的连接节点未进行安装偏差修正，滑移距离浮动更大，这是因为螺栓数越多，安装偏差造成的间隙变化越多，加大了模拟难度。但其他参数同一颗螺栓类似，能与试验结果吻合较好。

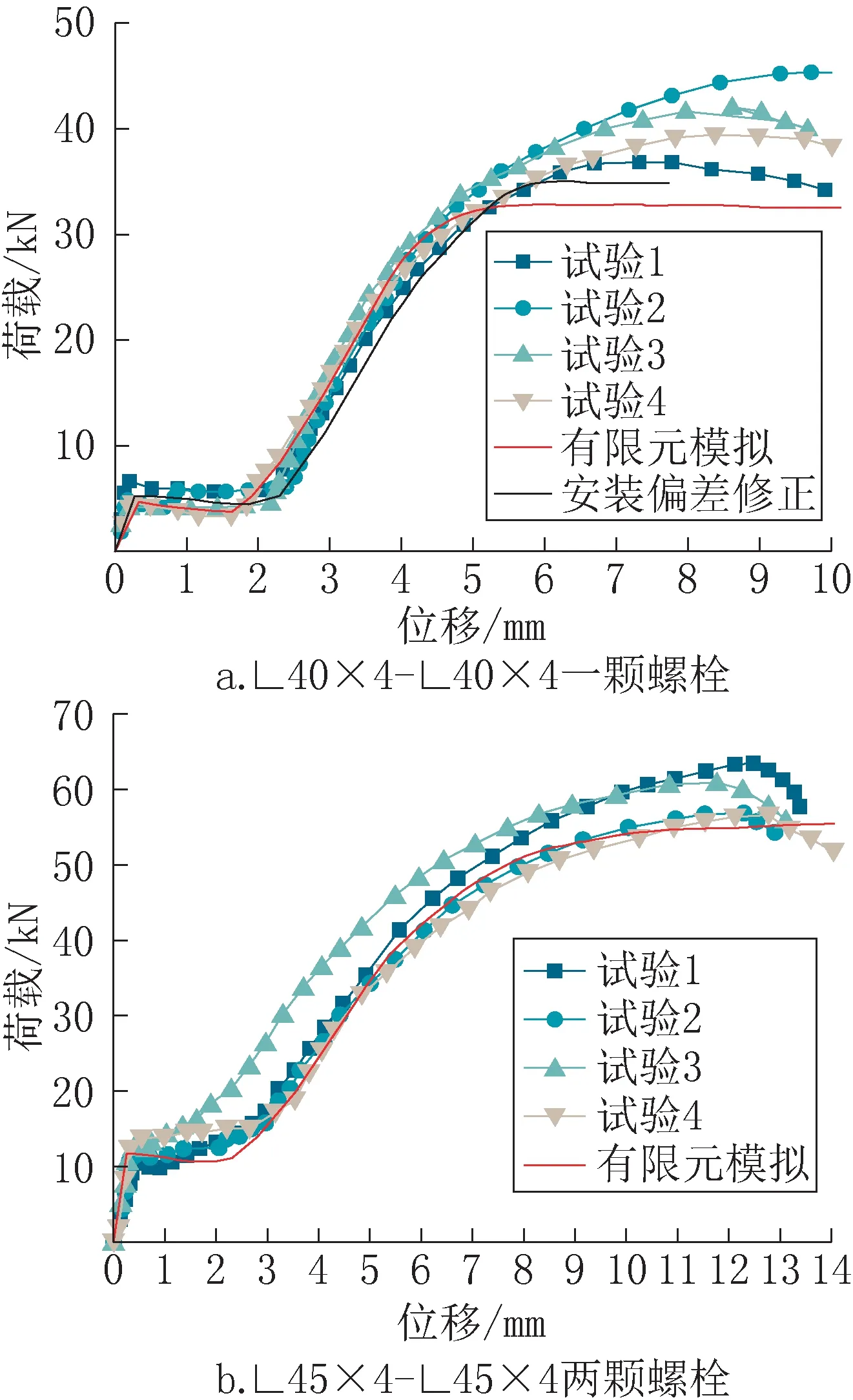
图11 试验与模拟的荷载-位移曲线对比Fig.11 Comparison of load-displacement curves between the tests and simulation

3.节点连接滑移曲线

表4 交叉斜材节间连接节点的滑移参数Tab.4 The data of the bolt slipping of the X-braced bar

为了更好地分析螺栓滑移对交叉斜材节间受力性能的影响，本文将节点连接滑移曲线优化为理想的变化关系，如图12 所示。

图12 交叉斜材节点连接滑移曲线Fig.12 The load-displacement curves of bolt slipping in the X-braced bar

2.2 交叉斜材的节点滑移模型建立

根据交叉斜材中等边角钢的受力特点和截面宽厚比大小，角钢选用SHELL181 壳单元进行模拟。材料的屈服强度和弹性模量设置为材性试验实测值，钢材密度为加工厂给出的真实值，泊松比取0.3，本构模型选择双线性随动强化（BKIN）模型，根据材性试验的应力-应变曲线，切线模量设置为弹性模量的2%。试验中底部支座未发生变形，在有限元分析中将其弹性模量放大100 倍，以此保证构件破坏而底部支座不发生变形，同时减少应力集中，有利于计算收敛。

分析试验工况，斜材承受来自螺栓和螺孔接触面的轴向挤压，因此选择在斜材上端部螺孔周围的节点施加沿斜材轴向位移荷载，同时约束加载点在平面外和平面内垂直斜材两个方向的位移，保证加载始终沿斜材轴向。支座底部为固定端，约束底面所有节点的自由度。在斜辅材连接处施加COMBIN39 弹簧单元，用于模拟螺栓滑移。COMBIN39 单元用于约束荷载传递方向上的平动自由度，其荷载-位移曲线取上文算得的交叉斜材节点连接滑移曲线，其余两个方向的平动自由度耦合。平面内转动自由度放开，其他两个方向转动自由度耦合，以表征螺栓连接在另外两个转动自由度上能提供约束。有限元模型如图13所示。

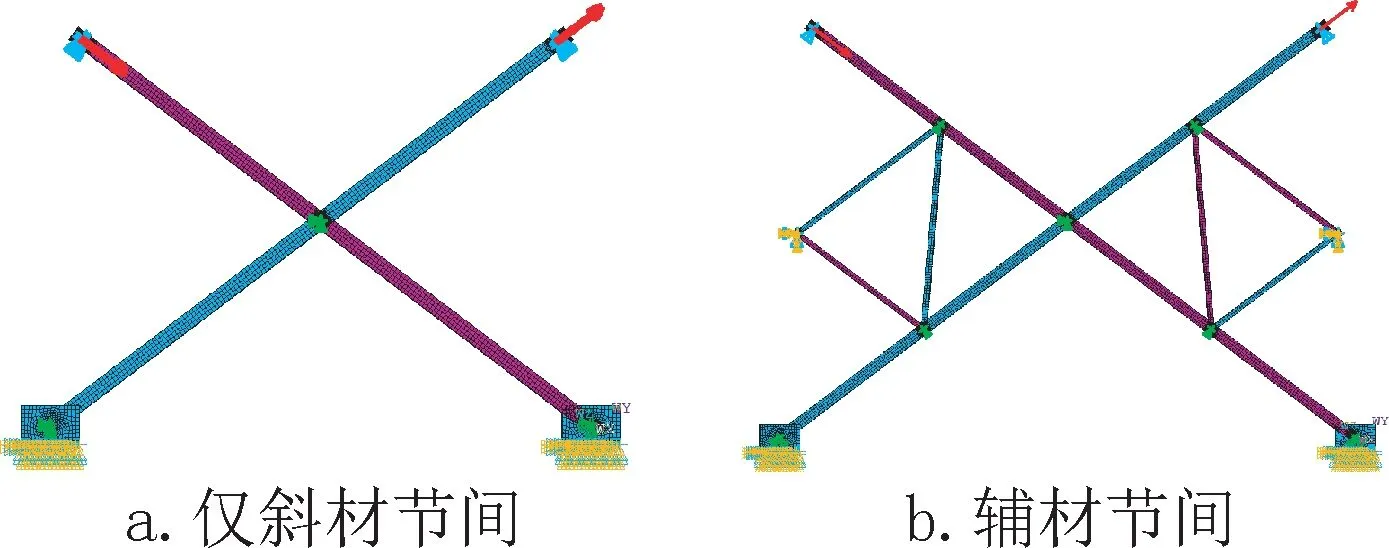
图13 有限元模型Fig.13 Finite element model

2.3 有限元分析结果验证

1.破坏形态对比

图14 列出一些工况下仅斜材节间的有限元结果和对应试验组的破坏形态对比，位移单位为mm。观察发现，随着拉压比增加，有限元计算结果中交叉斜材屈曲失效位置从压杆长段逐渐转移到交叉点，这与试验结果保持一致。

图14 仅斜材节间试验与有限元破坏形态对比Fig.14 Comparison of deformation between test and finite element of only diagonal section

图15 为辅材节间一些工况下的有限元结果和对应试验组破坏形态的对比，可以看出有限元分析的破坏模式与试验结果吻合。

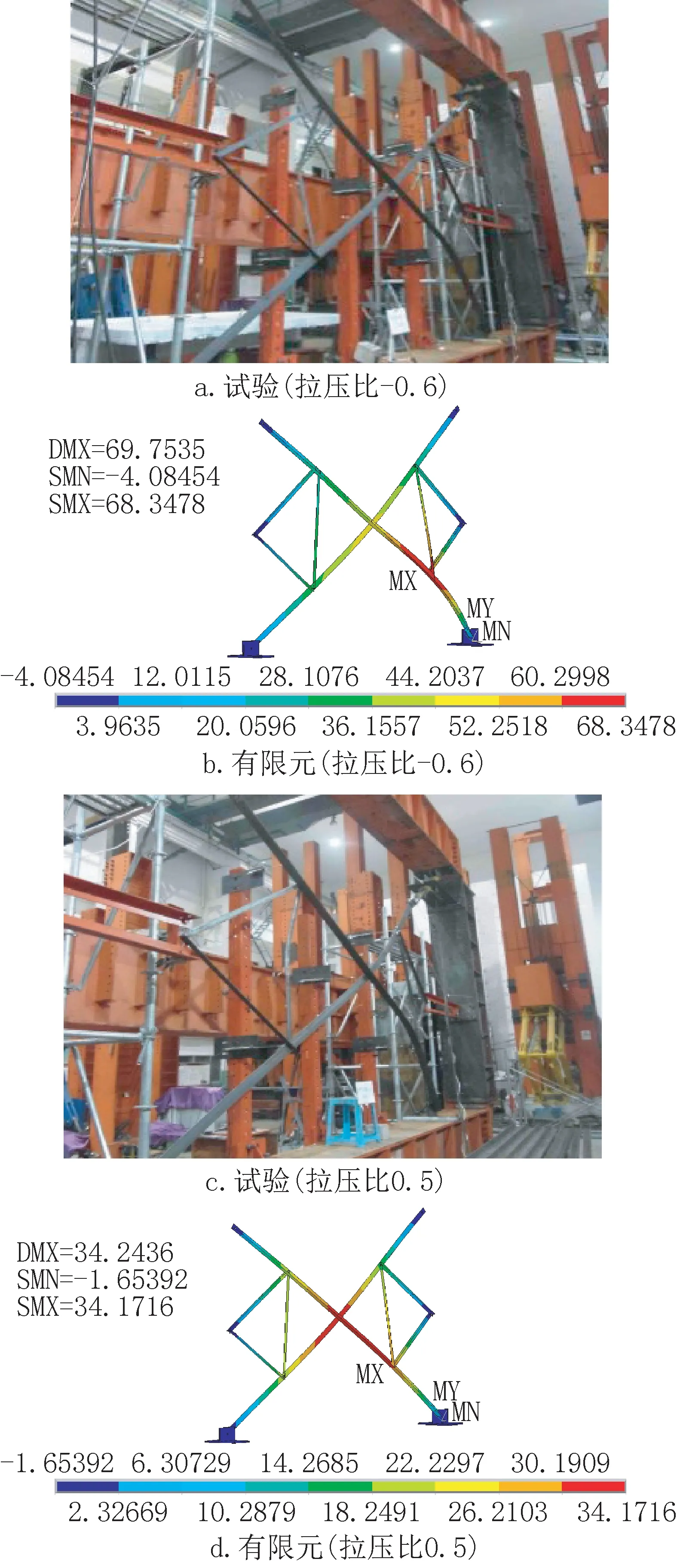
图15 辅材节间试验与有限元破坏形态对比Fig.15 Comparison of deformation between test and finite element of complex section

2.荷载-位移曲线

仅斜材节间典型试验组的交叉点和压杆长段测点的荷载-平面外位移曲线与有限元分析结果的对比如图16 所示，位移均取绝对值。由图16可知，仅斜材节间关键截面的荷载-平面外位移曲线有限元结果和试验结果较为吻合，这是由于仅斜材节间的构件长度较小，产生的误差也相对较小。有限元分析结果与试验结果整体变化趋势保持一致，到达极限荷载时对应的峰值位移大小接近，极限荷载位移随拉压比的变化规律也一致。辅材节间荷载-位移曲线同试验结果对比的相对误差要大于仅斜材节间，如图17 所示。两者达到极限荷载时对应的关键截面平面外位移不同，这是因为辅材节间长度更长，初弯曲更明显，控制轴向加载难度更大，以及辅材节间连接处增多，所产生的螺栓空隙也较多，最后导致偶然误差增大。但曲线整体变化趋势和反映的拉压比规律与试验结果保持一致。

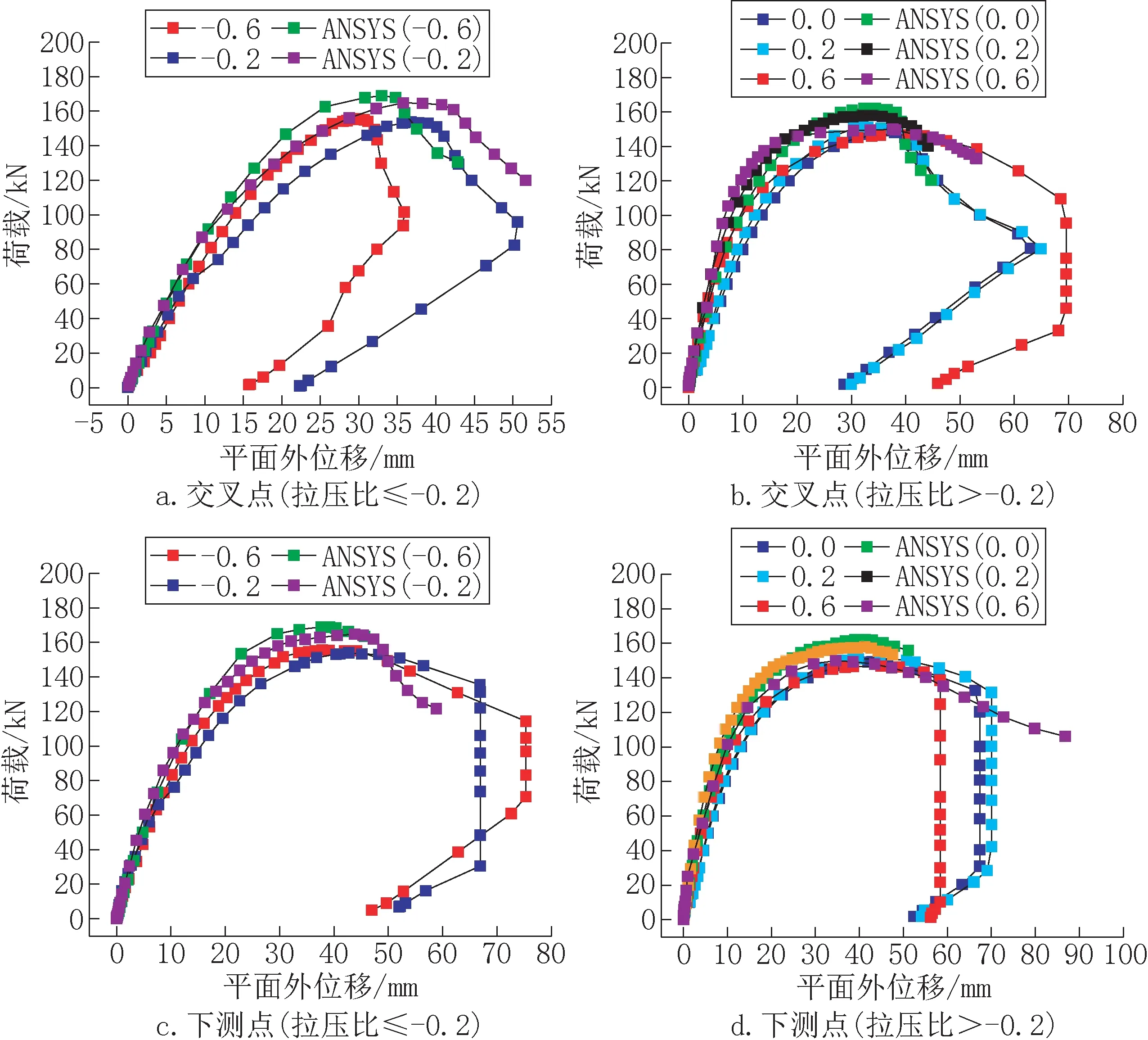
图16 仅斜材节间荷载-位移曲线对比 Fig.16 Comparison of load-displacement curves of only diagonal section

3.极限承载力分析

根据荷载-位移曲线的下降段确定各工况下有限元计算的极限承载力，对于调整收敛精度后仍收敛困难的曲线，选择最后一步荷载子步作为极限荷载。有限元计算结果与试验结果的对比见表5。

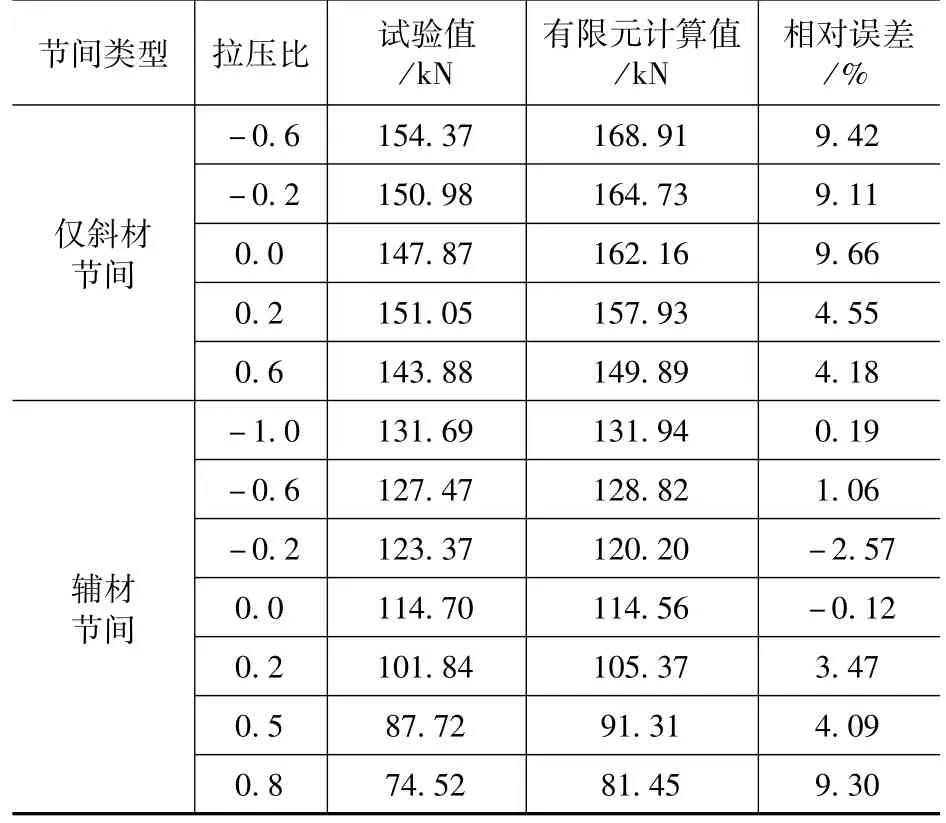
表5 交叉斜材极限承载力试验结果与有限元结果对比Tab.5 Comparison of stability capacity between test and finite element method

分析表5 可知，有限元计算承载力与试验结果吻合良好，但仍存在一定误差。有限元计算产生误差的原因，总结为以下几点：试验不是绝对的轴向加载，在加载端不免会产生一定程度的偏心或扭转，导致交叉斜材加速破坏，极限承载力降低。用于试验的角钢长细比较大，长度较长，搁置时间久了会产生初偏心，影响角钢承载能力。试验中人员操作存在偶然误差，加载速度的控制会造成拉压比浮动，加载前的人工对中同样会影响承载力大小。试验材料具有离散性，会对试验结果产生影响。

总体来说，交叉斜材的滑移模型模拟结果较为准确，相对误差不超过10%，可以推进到下一步研究。为节约篇幅，后续的参数分析仅考虑工程常见的辅材节间形式。

2.4 参数分析

影响交叉斜材节间承载力的因素有很多，本文重点分析拉压比、长细比、宽厚比和材料强度等因素。在参数分析过程中严格遵循单一变量原则，并对极限承载力的发展趋势做出定性分析。

1.拉压比及长细比

控制各构件截面及材料强度不发生变化，仅改变斜材设计的名义长细比来计算节间的极限承载力，并对拉压比进行细化，模拟两种节间在拉压比从－1.0 至1.0 的破坏形态，间隔为0.1。分别计算辅材节间在斜材长细比为80、90、100、110、120 时的极限承载力（前文试验件长细比为110），不同斜材长细比下交叉斜材节间极限承载力随拉压比的变化曲线如图18a。

分析单根曲线可知，辅材节间极限承载力随拉压比增大而减少。当拉压比≤－0.2 时，极限承载力受拉压影响较小；当拉压比＞－0.2 时，极限承载力随拉压比变化幅度增大。《架空规范》在拉压比≤－0.2 情况下没有考虑拉压比变化对交叉斜材承载力的影响，这与试验结果及有限元计算结果均有出入。

分析不同曲线可知，减小长细比能提高交叉斜材节间的极限承载力，且极限承载力随着长细比减小按照一定比例增加。长细比越小，承载力随拉压比的变化曲线越接近S 型曲线，即拉压比绝对值越大，承载力受拉压比影响越小。

2.宽厚比

为探究宽厚比对交叉斜材节间承载力的影响，改变斜材厚度来计算其极限承载力。取80 ×10、80 ×8、80 ×6、80 ×5，加上试验截面80 ×7，一共五种截面，对应的宽厚比分别为6、8、9.43、11.33、14。为保证单一变量原则，取单位面积承载力作为分析对象，以消除截面面积改变带来的影响。经计算可知改变肢厚对截面回转半径影响不大，即斜材长细比基本不变。

图18b为两种节间在不同斜材截面规格下单位截面面积极限承载力随拉压比的变化曲线。分析表明，对于辅材节间，减小宽厚比能较明显提高交叉斜材单位截面面积极限承载力，且单位截面面积极限承载力按照宽厚比的增加按比例减小。

3.材料强度

在Q355 材料强度基础上增加应用广泛的Q235 和高强角钢Q420 材料，保持其他参数不变，对辅材节间的极限承载力进行分析。极限承载力随拉压比的变化曲线如图18c。

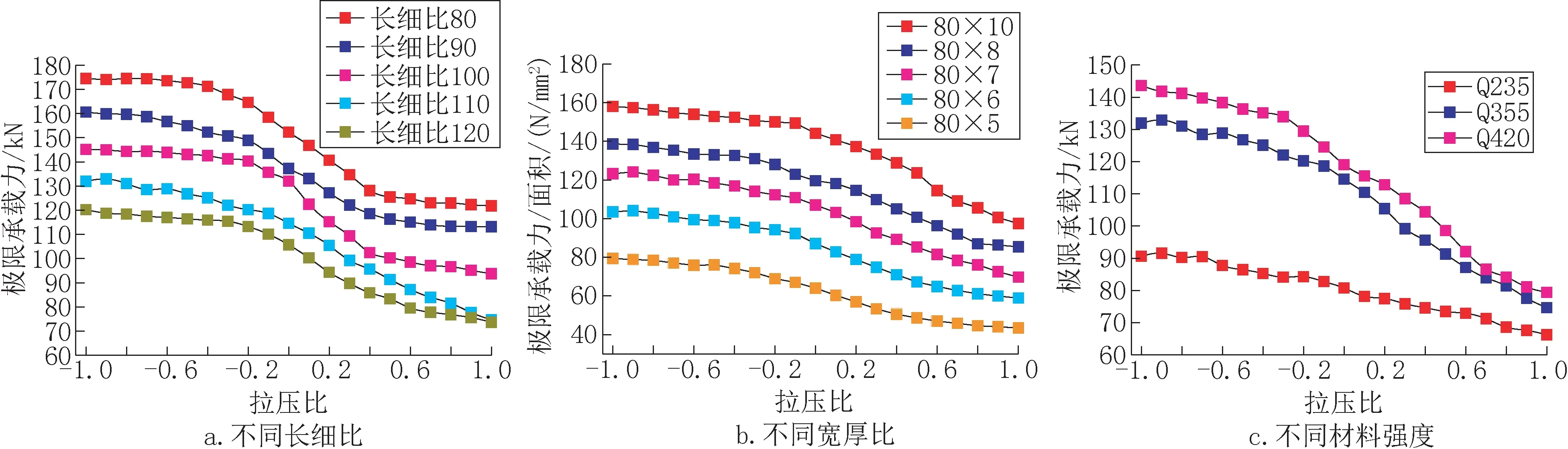
图18 交叉斜材极限承载力Fig.18 The ultimate bearing capacity of the cross-bracing

分析可知，对于交叉斜材辅材节间，在同样的拉压比情况下，极限承载力随材料强度增大而增大。Q355 和Q420 承载力较为接近，远高于Q235 钢材，可见当材料强度达到一定值后继续增大材料强度对极限承载力的提高程度有限。

3 结论

本文完成了交叉斜材节间试验，并将试验结果与我国现有的设计规范的计算值进行比较。利用有限元软件ANSYS建立了交叉斜材滑移模型，在验证有限元模型可靠性的基础上进行了参数分析，得到了以下主要结论：

1.交叉斜材仅斜材节间都是压杆的长段发生屈曲破坏，屈服位置都从压杆长段的中间开始，当拉压比≤－0.2 时，压杆绕最小轴失稳，其他情况为绕平行轴失稳。辅材节间破坏模式与拉压比有关，当拉压比≤－0.2 时，发生压杆长段屈曲破坏，反之则发生整体屈曲破坏。辅材节间的失稳破坏均绕平行轴展开，压杆呈S形失稳且拉压比越小趋势越明显。

2.《钢规》和《架空规范》对交叉斜材节间承载力计算值均与试验值存在误差。规范在一些工况下的计算方法与试验所得的破坏模式不符。

3.本文建立的交叉斜材滑移模型对两种节间的破坏形态、荷载-位移曲线以及极限承载力进行了等比例分析，其计算结果与试验结果吻合，极限承载力相对误差小于10%，验证了有限元分析模型的有效性。

4.通过交叉斜材滑移模型参数分析可知，交叉斜材辅材节间极限承载力随拉压比、长细比增加而减小，随材料强度的增加而增加，与宽厚比成负相关。