一种改进的双边滤波预处理新方法

刘 晨

（喀什大学计算机科学与技术学院，新疆喀什 844000）

图像去噪是图像处理领域的基础问题.图像中的噪声妨碍了图像处理的正常进行，影响了图像的人工判读和计算机解译，因此，图像滤波去噪是图像处理分析过程中的首要任务.近年来人们提出了众多的滤波方法来去除图像中的噪声，如各向异性扩散滤波器［1］、基于图像块的非局部均值滤波方法［2，3］、基于随机场的滤波方法［4］和双边滤波［5］.

双边滤波噪声抑制算法因具有良好的边缘保持效果，被广泛用于图像分析处理中.该算法在空间欧式距离的基础上结合当前点与其领域点的亮度相似性，对亮度距离和空间距离进行加权平均.该算法可以区分匀质平坦区域和边缘结构区域，从而在不同的区域结构进行不同程度的滤波，起到对图像边缘结构的保护作用，具有较强的适用性.双边滤波结合了图像像素间的灰度相似度和空间临近度这两个与图像中像素灰度密切相关的重要方面，从而在滤除图像噪声的同时保持图像的细节特征.近年来，出现了很多双边滤波的改进算法，文献［6］提出了在对噪声图像进行双边滤波前先进行高斯滤波，使用高斯滤波结果作为当前像素点的估计值，邻域值仍然使用原始噪声图像；文献［7］提出二次迭代滤波概念，即用第一次双边滤波的结果指导第二次双边滤波；文献［8］中提出了结合中值滤波思想的双边滤波；文献［9］中对双边滤波中的参数优化选择处理而达到对双边滤波的改进.

经典的双边滤波算法中相似性函数由像素与其邻域像素的灰度差定义，其计算方法是基于像素的，噪声的存在影响加权系数的准确计算，这种相似性度量函数定义不能准确地表达像素之间的实际相似性，故滤波结果的边缘结构保持效果没有得到显著的提高，算法在抑制噪声的能力上有一定程度的削弱.本文在双边滤波算法中像素结构相似性度量基础上，引入描述图像结构信息的结构相似性指数（SSIM），并重新定义双边滤波中的相似性函数的计算方式，从而达到对噪声的抑制.由于在实际现实中，噪声是客观存在的，在噪声图像中进行的结构相似性计算与其真实值之间存在一定的偏差.针对这一问题，本文进一步采取基于两级的改进双边滤波方法，以削弱噪声对相似性函数计算的影响从而提高算法的去噪性能.

1 双边滤波

双边滤波［5-6］是在诸如均值高斯滤波基础上考虑图像像素间亮度的关系，将Domain filtering和Range filtering 结合起来的一种滤波方法.

Domain Filtering表示为：

式（1）中，c（r，x）表示中心像素x与其邻近像素r的空间距离函数，

Range filtering表示为：

如何做好溃坝应急管理工作，涉及面很宽，上述简要论述乃非工程措施的一部分内容。从根本上说，所有大坝管理者都应当居安思危，未雨绸缪，防患未然，能及时发现大坝风险先兆才能取得主动。

上述两种滤波方法中，f（r）表示在r处亮度值，h（x）表示在x处滤波后的亮度值.

结合上述两种滤波算法思想产生新的所谓双边滤波，故双边滤波可表示为：

在本文中Domain filtering 以高斯滤波为例，则c（r，x）定义为：

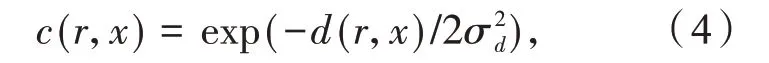
相似性函数s（（fr），（fx））定义为：

2 改进的双边滤波

经典的双边滤波虽然在去噪的同时能保持图像的边缘结构信息，但其算法是基于像素水平的，图像的结构保持效果没有得到显著的提高，同时噪声的存在会影响加权系数的准确计算，降低了该方法对噪声的抑制能力.根据文献［2，3］可知，可以使用基于图像块的方法来削弱噪声对图像结构相似性度量的影响.针对双边滤波中存在的这一现象，本文在考虑图像结构信息的基础上，引入结构相似性指数（SSIM）这一评价图像结构相似性的度量参数.文献［10，11］中提出了结构性相似性指数（SSIM）这一参数，其将亮度、对比度和结构信息结合起来评价图像相似性，SSIM 定义为：

式（6），中ux和分别表示以像素x为中心的方形邻域Nx的灰度均值和方差，σrx表示邻域Nx和Nr的灰度协方差，C1和C2为极小的常数防止零除的特殊情况.

经典双边滤波方法中Range filtering 使用相似性函数来描述图像像素间的结构性的异同，其使用加权的欧氏距离来定义结构相似性.相似形函数中d（f（r），f（x））越接近0，则两个像素点的结构相似性越好.根据文献［10，11］可知SSIM的取值区间范围为［-1，1］，当SSIM 绝对值越大，则表明两个小块的相似性越好，故为了和原先双边滤波中的基于加权的欧氏距离一致，重新定义结构相似性参数为：

NS（r，x）取值区间为［0，1］，当NS（r，x）越大时，两个小块的相似性越低，也就是两个像素点的结构相似性越低，通过使用图像块的定义来削弱噪声对像素间结构相似性计算的影响.

通过上述的描述则基于加权的欧氏距离作为相似性度量的公式可重新表示为：

式（8）中，||*||为欧式距离，E［NS（r，x）］为归一化常数，其计算式为

经过上述改进后代替原先双边滤波中像素间结构相似性度量进行计算.

通过使用结构相似性指数重新定义双边滤波中像素结构相似性度量函数，但是在噪声图像中进行相似性函数的计算，其准确性不可避免会受到噪声的干扰.在噪声图像中，相似性函数的计算受到噪声影响可以通过下面这个例子来说明.

图1（a）为一幅512*512的Lena图像，图1（b）是添加均值为0 方差为0.1的高斯噪声.为了更好地展示细节，图中间含有帽檐和眼睛的放大显示分别如图2（a）和图2（b）所示.对噪声图像图1（b）使用本文提出的改进的双边滤波方法进行去噪处理.相似形函数的度量计算中使用的样本分别基于无噪声图1（a）和噪声图1（b），图2（c）显示了基于无噪声图像相似性度量计算的滤波结果.从实验结果可知，在没有噪声干扰的情况下，使用结构相似性指数进行改进的双边滤波可以获得优异的去噪性能.然而实际情况对结构相似性的度量计算只能是基于有噪声图像的，其相应的滤波结果如图2（d）所示.为了削弱噪声的影响，本文提出了一种基于两级的改进的双边滤波方法，该方法的流程如图3 所示.

图1 Lena 图像

图2 相似性计算的准确性对去噪的影响

图3 基于两级的改进双边滤波方法

第一级改进的双边滤波将噪声图像进行滤波处理，结果为

然后在滤波结果上进行像素相似性函数度量计算，并传递给第二级改进的双边滤波，获得最终的去噪结果

基于两级的改进的双边滤波方法中第一级滤波的目的是降低噪声，通过第一级降噪的处理削弱了噪声对像素结构相似性度量计算的影响，提高了相似性度量计算的准确性.

3 方法的实验评价及分析

3.1 实验设置

将提出的基于两级的改进的双边滤波方法（NB）和经典的双边滤波［5］（SB）、文献［6］方法（GB）和文献［7］方法（DB）进行比较，滤波中的滤波窗口尺寸选取为典型的7*7.对于结构相似性指数（SSIM）窗口选取5*5.

3.2 评价准则

选用峰值信噪比（PSNR）［5］和EC［12］两个准则来评价各方法的噪声抑制性能，峰值信噪比用于评价去噪的整体性能，EC 用于评价边缘结构保持方面的性能.

峰值信噪比（PSNR）的定义为

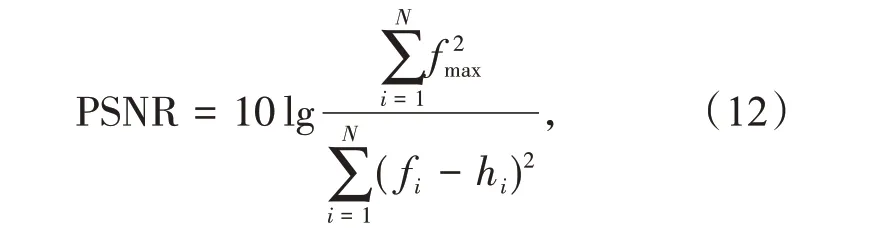
式（12）中，N表示图像的像素总数，fi和hi分别表示噪声图像和去噪图像的像素值，fmax为噪声图像像素灰度最大值.

PSNR 是衡量对整幅图像噪声的抑制能力，PSNR 越大，表示抑制噪声的能力越强.所以在评价标准中，PSNR越大越好.

文献［12］提出的EC 评价方法，其定义的基本公式为

式（13）中，Γ为相关函数，分别表示无噪声图像x和去噪后图像u的梯度值，分别为相应的均值.EC通过梯度的相关性考察边缘的相关性，其取值范围为［0，1］，值越大表示边缘结构保持性能越好.

3.3 参数的选择

双边滤波算法中，涉及σd和σr两个参数，根据文献［13］，σd对最优的σr影响不显著.图4 是本文算法选取不同σd和σr参数值得到的PSNR 值和EC值，由图中的数值可以得出，不论σr参数取什么值，σd的值大于3 时，对PSNR 和EC 值改变不再显著，同文献［13］探讨可知，其对最优的σr影响不显著.由本文实验推荐σd的值设为3～5.本文中使用4.在各种双边滤波算法中，边缘结构保持性能主要有σr决定，而σr的选取是一个难点.σr的值过小，则图像边缘保留较好，但是滤波器的平滑能力较弱，不能有效的消除噪声；σr的值过大，则容易造成过平滑，不利于保持图像边缘结构信息.文献［14］中使用局部相位参数，文献［15］使用局部滤波参数自适应调整，但是这些自适应参数本身的建立也需要人为设定具体参数数值.故本文采用实验数据合理取得σr的具体取值.由图中不同σr的取值得到结果值，本文选取σr值为200.

图4 参数的选择

3.4 实验结果

对图1（a）所示的512*512 标准Lena 图像，添加均值为0，方差分别为0.04、0.1 和0.3的高斯噪声，合成具有不同噪声水平的图像.分别采用经典的双边滤波［5］（SB）、文献［6］（GB）方法、文献［7］（DB）方法和本文提出的基于两级的改进的双边滤波（NB），根据PSNR 和EC 评价标准，各方法的去噪性能如表1 所示.图5（a）（b）（c）（d）是在添加噪声方差为0.1 得到含噪图像（图1（b））采用不同算法得到的去噪结果.

从表1 所列结果可以看出，在不同噪声水平上，本文提出的方法无论是在整体去噪性能（PSNR）还是边缘信息（EC）保持均优于SB、GB 和DB 方法.特别是在噪声水平为0.1 上，相较于其他三种方法，本文方法性能得到大程度的提升.表中的数据表明本文方法在消除图像中的噪声同时能有效保持图像的边缘结构信息.图5（a）（b）（c）（d）是分别采用SB、GB、DB 和本文提出方法（NB）得到的去噪结果图，从图中可以看出，各个方法都能消除图像中存在的噪声.图5（e）（f）（g）（h）是其对应的局部放大图，从滤波结果局部放大图像中可知，相较于经典的双边滤波方法（SB），GB、DB 和本文方法能更好地平滑图像.对于GB、DB 和本文方法而言，GB 显然是过平滑.而相较于DB 方法，本文方法不仅能保持图像的边缘结构信息，如图中帽檐部分，而且在整体上能更好地平滑图像，如图中面部部分.从表中数据和滤波结果都可以看出，本文方法在有效消除噪声同时也能有效地保持图像的边缘结构信息.

图5 噪声图像图1（b）的去噪结果

表1 不同去噪方法在添加不同噪声水平的Lena图像上的性能比较

4 结论

本文提出了一种基于结构相似性指数的改进的双边滤波新方法.原先双边滤波中相似性函数的计算度量是基于像素的，容易受到噪声的影响.本文使用结构相似性指数改进双边滤波中的相似性度量，能够利用结构信息来削弱噪声对相似形函数计算的影响.为了进一步削弱噪声对滤波的影响，采用基于两级的改进的双边滤波方法，能提高滤波方法的相似性函数计算的准确性.实验结果表明，本文提出的方法在抑制噪声的同时能更好地保持图像的边缘结构信息.