基于统计学习方法的模型构建与数据分析

姚 瑞，唐 泉

（新疆师范大学 数学科学学院，乌鲁木齐 830017）

统计学习，也称为统计机器学习，在计算机及其应用领域中具有重要意义.统计学习[1]的主要方法是基于数据建立统计模型来预测和分析数据，由监督学习、非监督学习、半监督学习和强化学习组成,包括k近邻法、朴素贝叶斯方法、支持向量机等方法.半监督学习是一种同时兼顾标签样本和无标签样本的学习方法，利用标记样本的优点来精确描述单个样本，同时使用大量无标记数据来进一步提高分类器的性能[2].半监督支持向量机（S3VM）最初应用于文本分类[3]，主要有梯度下降法（Gradient descent）[4]、确定性退火方法（Deterministic annealing）[5]和半正定规划方法（Semi-definite programming）[6]等研究方法.模糊支持向量机在传统支持向量机基础上提出，分类精度和回归精度更高，查翔等[7]提出了一种基于多区域划分的模糊支持向量机方法；谭萍等[8]结合模糊C-均值与FSVM 提出了一种多级的模糊支持向量机对说话人进行语音识别；Muscat R 等[9]提出了分层模糊支持向量机模型.本文讨论支持向量机模型，对支持向量机模型的基本思想、发展完善及应用情况进行概述，并深入探讨一种通过识别误分类点来构造半监督的模糊支持向量机模型及算法实现.

1 模糊支持向量机

1.1 线性可分的模糊支持向量机

对于模糊训练集

模糊约束规划为：

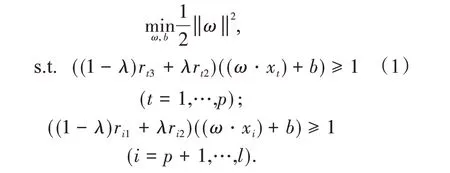
其中，λ(0 ≤λ≤1)为置信区间.

其对偶问题为：

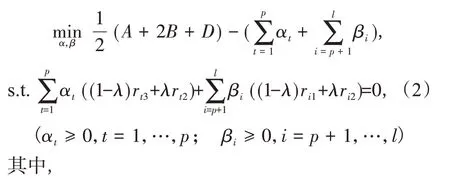
Step4：计算ω*和b*，如式（4）；

Step5：构造最优分类超平面(ω*·x)+b*=0，得到最优分类函数式（5）.

2.2 非线性可分的模糊支持向量机

对于模糊非线性问题，引入变换

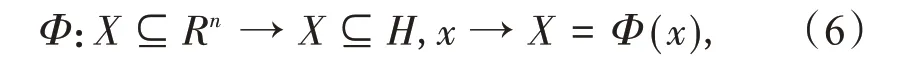
则对应的模糊非线性训练集变换为：

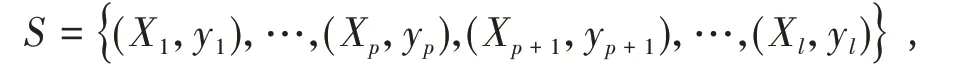
其中，Xi=Φ(xi) (i=1，···，l).在置信水平λ(0 ≤λ≤1)下，模糊分类问题转化为：

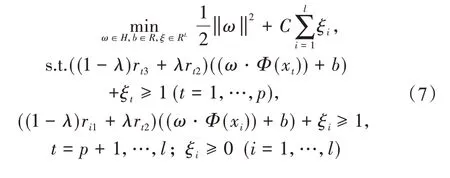
其中，C＞0为惩罚参数；ξi=(ξ1，…，ξl)T为松弛变量.

该二次规划存在最优解，通过取适当的核函数，使得K(xi，xj)=Φ(xi)·Φ(xj).可求得二次规划式的对偶问题为：

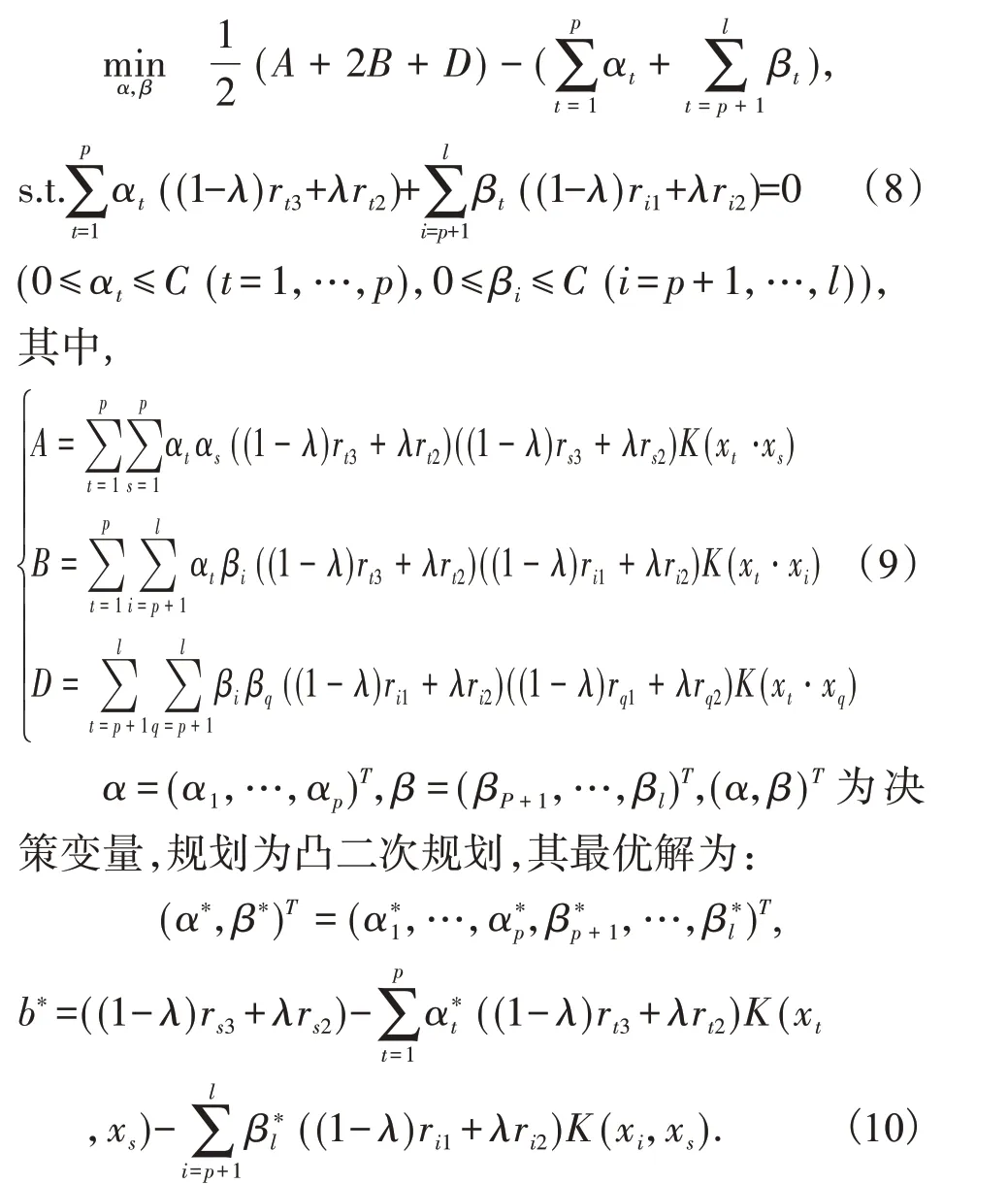
最优分类超平面为(ω*·x)+b*=0，令g(x)=(ω*·x)+b*，最优分类函数为:

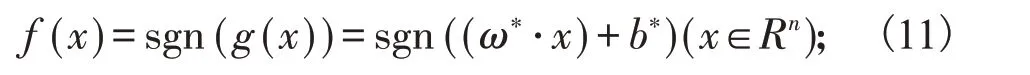
模糊支持向量机的算法：

Step1:构造隶属度函数，确定隶属度

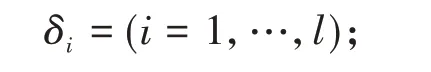
Step2：给定模糊非线性可分的训练集

Step3：求解线性规划式（8）得到最优解

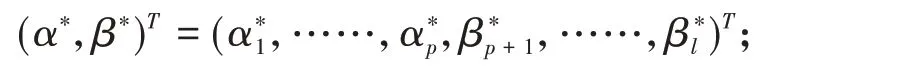
Step4:求解（10），计算b*；

Step5:构造最优分类超平面(ω*·x)+b*=0，得到最优分类函数式（11）.

2 一种半监督模糊支持向量机的模型

2.1 半监督支持向量机模型

由于可疑的误标记点仍包含有用信息，如特征位置信息，在数据分类中仍起重要作用，为充分利用可疑的误标记点，下文使用位置信息的方法获得最佳分离.

对于集合S中任一点，保留位置信息xi，删除标签yi.令Xl=S表示所有标签训练点数据集，Xu={1，…，n} 是无标签训练点的数据集.假设令yi表示标签向量，软间隔的半监督二次曲面支持向量机(SSQSSVM)模型:

2.2 分支与界定算法

令α≥0n为拉格朗日对偶变量，则问题（12）的拉格朗日函数可写为：

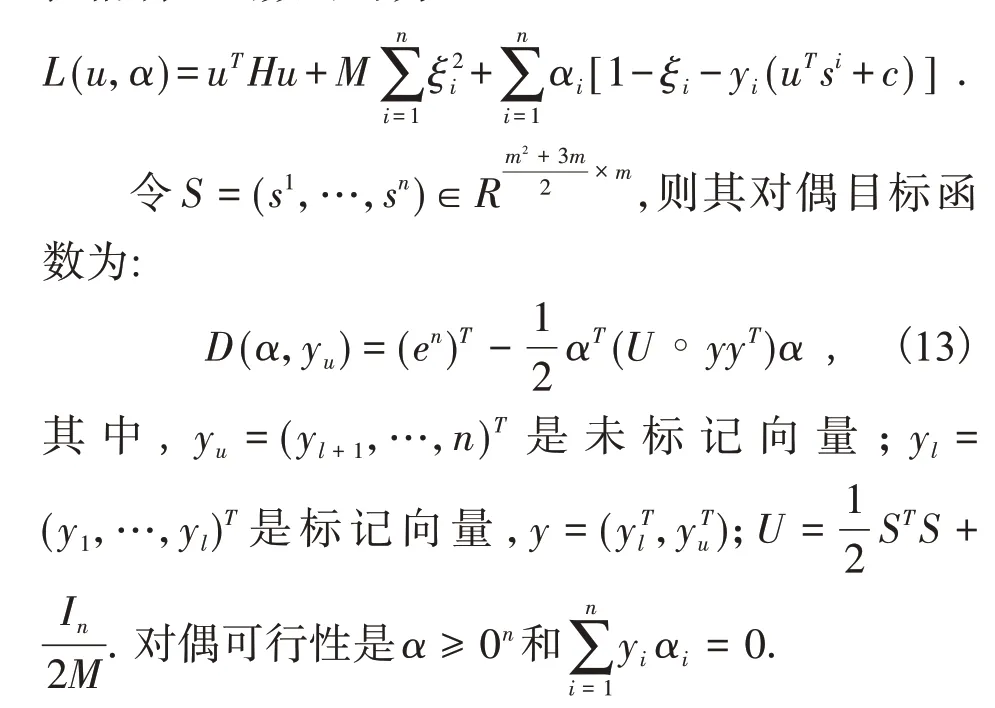
对于一个给定的yu，任意向量α(yu) 使D(α(yu)，yu)≤maxαD(α，yu).

SVM 最优值为下界，所有叶节点中目标函数的最优值为上界.

2.3 半监督模糊支持向量机算法

输入：训练数据集(xi，yi) (i=1，…，n)；ε.

Step1：用CL-stability 算法检测训练集中可疑的错误标记点并删除标签.获得数据集Xl和Xuχu.设k=1，U=+∞.将原始问题重新定义为（12）.

Step3:找到具有最小下界L的节点.如果U-L＜ε，则在该节点获得返回值uˉ，算法停止并进行Step4；否则，遵循深度优先策略到达下一个节点.给无标记的点si分配标签yi，用分支相应的si及标签-yi探索相反的分支.返回Step2.

Step4:通过分解（14）中的uˉ得到原始空间中的分离二次曲面.

3 算法的MATLAB实现

3.1 MATLAB中的SVM算例

图1 和图2 是人工数据集分类结果，准确率达到100%.

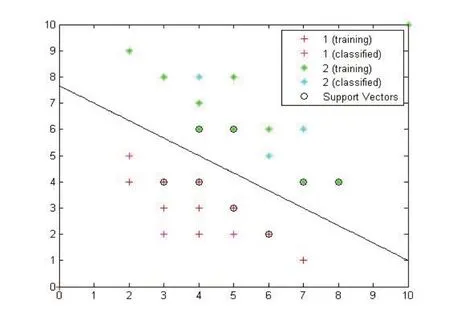
图1 线性可分支持向量机

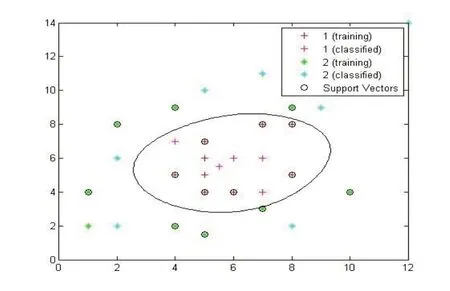
图2 线性不可分支持向量机

图3 使用Iris 数据集，在实验精度0.80的阈值下，选取数据中前两个特征值，进行实验.

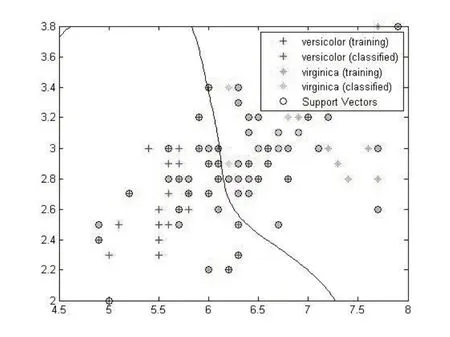
图3 Iris数据集实验

3.2 实例分析

本节将支持向量机应用到国有企业管理者的考评系统中，将企业管理者的表现分为优、良、中、差四个等级，由于支持向量机是二分类模型，所以需要将多个支持向量机以子分类器的形式加以组合.

表1将14家国有控股企业的管理者作为样本,数据来源于毛惠媛对东北地区企业家管理创新机制的研究[10],用支持向量机对企业管理者的绩效进行考核等级的分类处理.

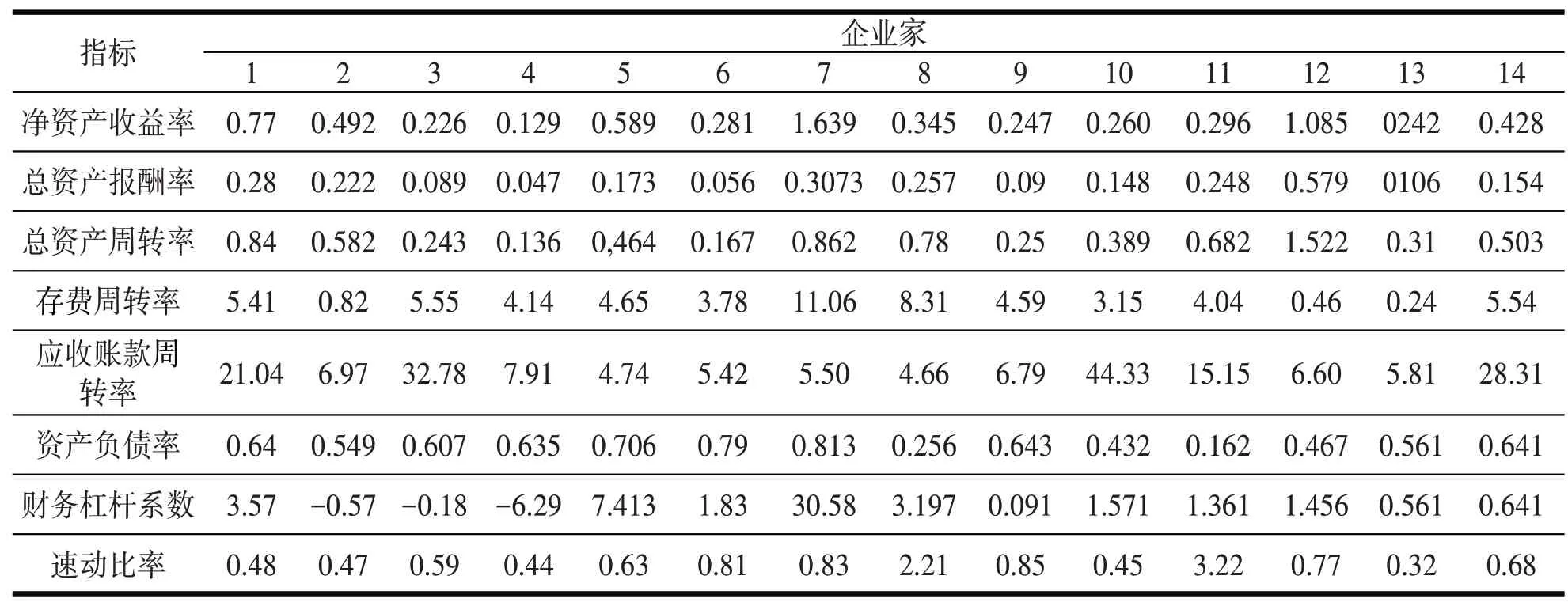
表1 国有企业管理者评价指标得分表

由表1 可以看出,对企业管理者的考评打分的量纲是不同的,为了消除这一偏差,我们先对所有数据进行归一化处理,得到如表2中数据.

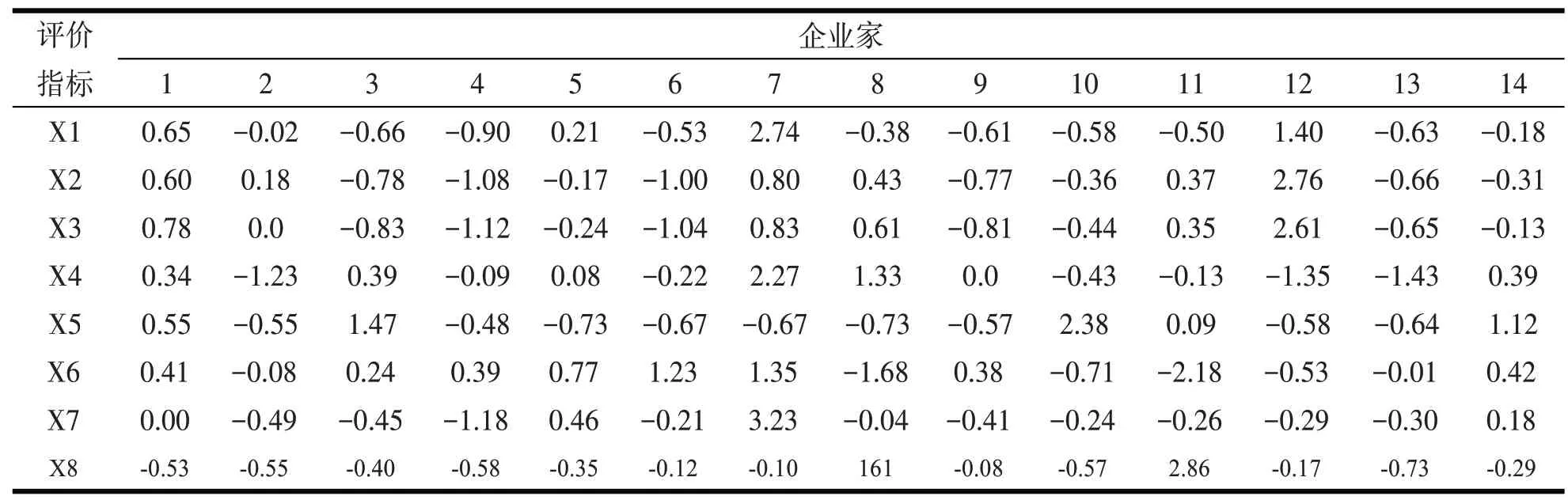
表2 国有企业管理者评价指标得分归一化处理结果

在给出的14 位企业管理者的数据中,首先选定1～12 号企业管理者的数据作为训练数据,13 号与14 号企业管理者为测试数据集.1—3 号企业管理者的分类为优;4—6 号企业管理者的分类为良,7—9 号企业管理者的分类为中,10—12 号企业管理者的分类为差.

将上述分类数据两两组合构造子分类器,既构造优-良、优-中、优-差、良-中、良-差、中-差六个分类器,对进行数据训练.由于上述训练数据集可能存在误分类数据,于是可以构造模糊支持向量机,将测试集分别带入6 个子分类器中,出现频数最多的分类结果认定为对企业管理者绩效的分类最终结果.训练得到六个子分类器的分类阈值分别为:-0.0244;-0.0082;-0.0214;0.5579;-0.2947;0.479.(详见表3)

表3 测试集分类结果

从表3知，13号企业管理者的绩效考核分类结果为“差”，14 号企业管理者的绩效考核分类结果为“中”.

4 总结

本文提出的半监督模糊支持向量机方法有效地缩短了计算时间，该算法比基准SDP 松弛方法更高效.另外，本文将SVM 方法应用于企业管理者的表现等级评定系统这一实际问题，得到较好的分类结果.但该方法处理大规模的数据集（n＞＞1000）方面受限制.后续，我们将考虑如何解决此问题.