函数有唯一零点问题的多视角分析
陕西省西安市第八十九中学 (710003) 彭文静
函数零点是连接函数与方程两大问题的桥梁,是高考复习的热点问题,该知识往往渗透于综合题中,对学生逻辑思维能力要求高.函数y=f(x)为零的自变量x的值即为函数的零点,即方程f(x)=0的根,也即y=f(x)图像与x轴交点的横坐标.其等价关系如图:

函数零点的多角度分析过程体现了转化与化归、数形结合、分类讨论等数学思想方法,笔者以一道函数零点问题为例从四个方面进行剖析.
1、题目呈现
题目当x∈(1,+∞),函数f(x)=xlnx+(1-k)x+k有唯一零点,求距离k最近的整数.


2、具体解法
视角1:直接切入找零点,分类讨论需谨慎
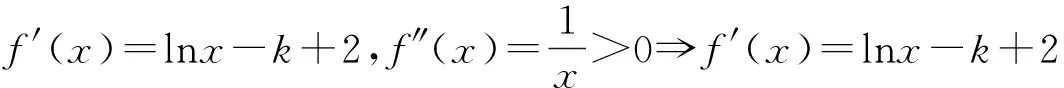

点评:该解法中依据k-2与0的大小关系,将参数k分两种情况讨论.其中在情形②中,f′(x)=lnx-k+2=0在(1,+∞)有且只有一个解,该方程为超越方程,则要“虚设”零点,设而不求,然后由函数f(x0)单调性,借助零点存在性定理,凭号定论零点存在区间,这是解决该问题的核心思想,最后就是利用二分法进一步缩小根的存在区间,以此确定k的整数值.
视角2:函数角度求交点,数形结合显直观

图1
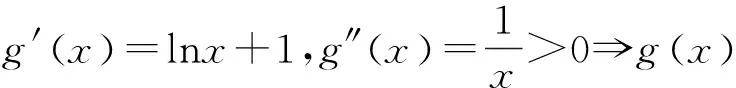
点评:该方法清晰明快,避免了参数的分类讨论,但找准两个基本函数是关键,一般以能画出两个函数图像为原则,如本题中的下凸函数图像和直线.
视角3:完全分参探性质,研究最值是关键

图2
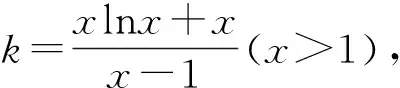
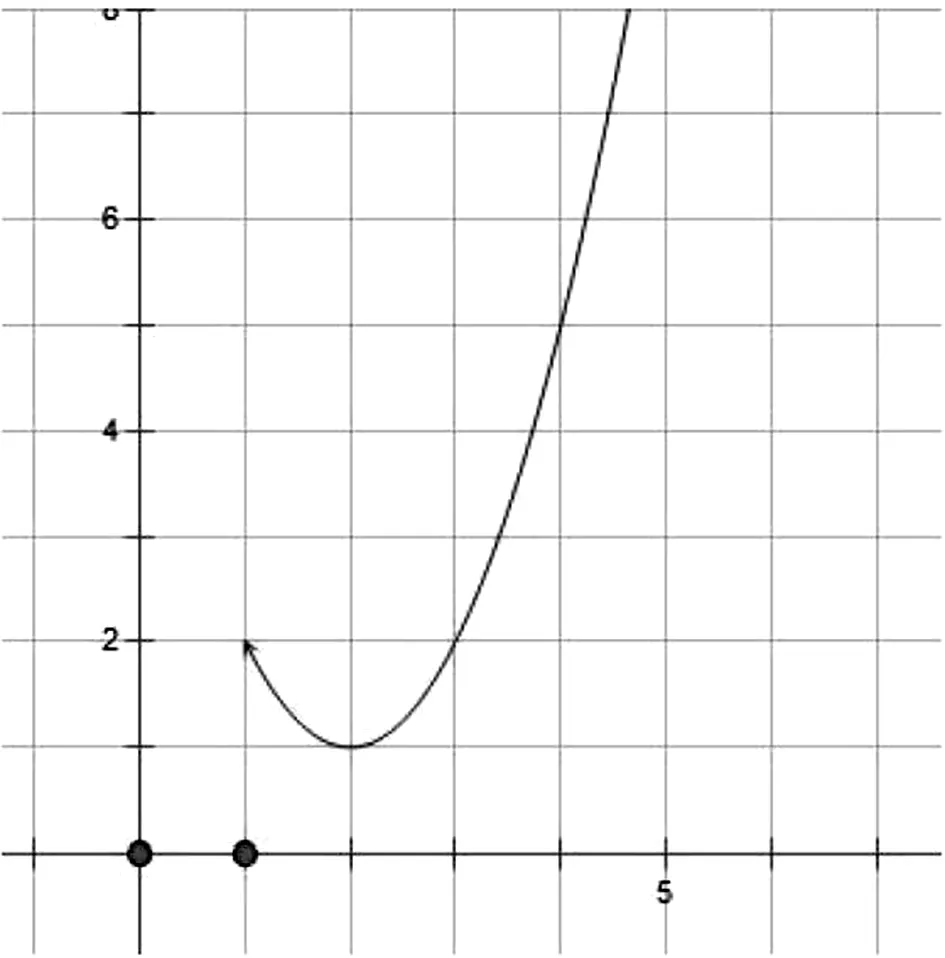
图3
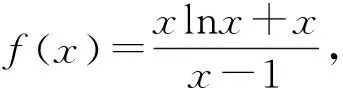
视角4:“降维”变形巧构造,等价转化是本质
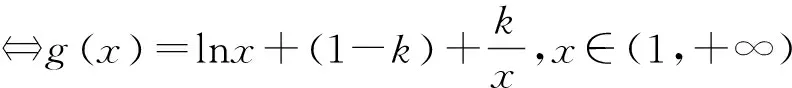
函数零点是连接函数与方程两大思想问题的桥梁,而已知零点个数唯一求参数的取值范围是函数零点问题的常见题型之一,其本质是函数单调性、极值、最值的应用,涉及到的具体思想方法有数形结合、分类讨论及转化与划归思想.本题从四个不同视角分析零点唯一性问题,解题方法迥异.其中,解法1直接切入普遍常规,学生易于着手,但解答完整还需较强的导数功底及逻辑思维能力,其中找准分类讨论的切入点和解决超越方程的“隐零点”是两个关键点;解法4进行等价变形后直接分析新函数的性质,本质与解法1相同,但比解法1简单原因是没有超越方程的出现,便于解决问题.解法2分离参数操作简单,备受学生青睐,直接求分参后新函数的值域或最值即可,但缺点在于新函数的最值可能无法求得,需要借助于“洛必达法则”,亦或是新函数解析式过于复杂,无法进行下去等等;解法3数形结合比较直观,唯一零点找临界可用切线法,但需要有较强的图形分析能力.
由函数零点的唯一性进而可以拓展到求函数零点个数问题,其基本解决途径如上,在做题过程中,对该四种解法的综合评估、确定最优解法的过程其实也是提高学生分析问题、解决问题、落实数学核心素养的途径.只要用心思考、灵活转换,抓住导数性质这一有力工具,则函数零点个数问题将不再是难题.

