一道直线与椭圆问题的解法与应用
江苏省海门中学 (226100) 蒯 龙
在直线与椭圆的题目中经常遇到三角形的面积问题,构造三角形的面积有多种途径,如果将三角形改为四边形,特别是一般的四边形,如何求其面积呢?本文通过一道考题的两种解法来说明如何处理四边形的面积问题.
一、问题与解

图1

(1)求|AB|(用k表示);

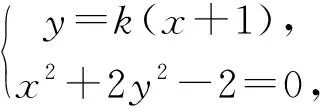
(2)设AB与CD交于点Q,AB和CD所成的角为θ,则SACBD=S△AQC+S△CQB+S△BQD+S△DQA

方法一:运用角公式得正切、求正弦,构造函数求范围

方法二:坐标变换将椭圆化为圆,基本不等式求范围


图2

评析:第2问的关键是表示出四边形的面积,方法一利用到角公式求得两对角线夹角的正弦值,进而利用斜率表示出四边形的面积,利用函数单调性求出取值范围;方法二,通过变换将椭圆的内接四边形转化为圆中对角线互相垂直的四边形面积,利用基本不等式求出取值范围.
二、解法推广


图3
证明:当ABCD是凸四边形时,(2)中已证,下证ABCD是凹四边形时的情形,如图3设AC与BD交于点E,则SABCD=S△AEB+S△BEC-S△AED-S△CED
上述命题说明任意四边形的面积就是以对角线平移后构成的三角形的面积,由解法二可得到三角形面积的坐标公式.


根据上述命题只需知道三角形3个顶点的坐标,便可以求出三角形的面积,解法二中依据上述坐标公式可以得到变换前后三角形面积之间的关系.
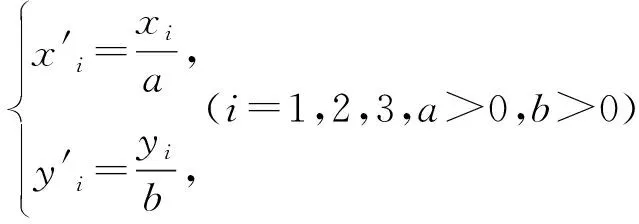

三、综合应用
例1 (2021广州市一模)已知点A(1,0),点B是圆O1:(x+1)2+y2=16上的动点,线段AB的垂直平分线与BO1相交于点C,点C的轨迹为曲线E.
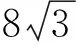







结语:涉及四边形的面积问题,关键在于如何表示面积,命题1与命题2用坐标表示四边形的面积,避免了讨论四边形的形状,运用了数形结合的思想,将几何问题转化为代数方法处理,体现了解析几何的思想.命题3中的变换,实现了将椭圆中的问题转化为圆中的问题,使得问题的几何特征更为明显,运用了转化与化归的数学思想.

