在有效生成中涵育数学核心素养

福建省闽清县第一中学 (350800) 林 婷 林青松

数学课堂是由“预设”和“生成”两个部分组成的.“预设”是教师根据学情和教学目标有目的、有计划地对课堂教学内容所进行的精心设计；“生成”是课堂预设的升华，使课堂教学“顺学而导”，是教学生命力与真正价值所在.数学教学过程具有复杂多变性，需要教师具有敏锐的课程意识、足够的教学智慧，寓有形的预设于无形的、动态的课堂教学中，营造出有利于学生发展的原生态课堂，为核心素养的落实找到出口与支点，从而完成数学教育立德树人的目标.

1 运用“问题导学”，在探究中生成

教材是严肃的、权威的，但并非“至圣”的金科玉律，如果照本宣科，就算再高明的教师，也是不可能把课上得很精彩.因此，教师应潜心钻研教材，在研究教材的基础上遵循学生学习数学的认知规律，将教学内容“问题化”，提出既能激发学生学习兴趣，又具有探究价值的“问题”，通过师生之间对“问题”的互动建构与合作交流，提升学生的“问题”意识，培养学生的探究能力，从而促进课堂生成.

案例1 人教A版必修第一册“函数的零点与方程的解”教学片断(引导学生探究零点存在性定理)

问题1 函数f(x)=x5+2x-1存在零点吗？如果存在，是多少？

师：数学史上，数学家们希望能像求解低次方程那样去解高次方程，但经过长期的探索，都没有得到解决.1824年，挪威天才数学家阿贝尔(N.H.Abel，1802—1829)成功地证明了五次及以上的方程没有根式解.那么，我们能否利用别的方法判断函数有否零点呢？

生1：可利用函数图象的性质判断函数的零点．

图1

问题2 图1为某地区从0时到12时的温度变化图，假设气温是连续变化的，请用两种不同的曲线将图形补充成完整的函数图象.在这段时间内，是否一定有某时刻的温度是0℃？为什么？

教师引导学生设计“两种方法”，激发了学生的探究热情.他们大胆尝试、操作.—种、两种、三种……，课堂出现了“未曾预约”的生成，其中包括在区间(a，b)内只有单一零点的函数图象(单调或不单调的)，也有多个零点的函数图象.教师对学生的各种画法进行展示(限于篇幅，文中只给出图2(1)、图2(2)两种连接方法).

图2(1) 图2(2)

问题3 若0时的温度与12时的温度都在零上(下)，是否一定有温度为0℃的时刻？

问题4 对于一般的函数y=f(x)，在区间[a，b]上有f(a)·f(b)<0，那么函数y=f(x)在(a，b)内必存在零点吗？

学生议论起来，一部分学生认为“存在零点”，另一部分则回答“不一定”.

师：请大家举例说明.

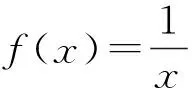
问题5 对于一般的函数y=f(x)，满足什么条件时，函数f(x)在区间(a，b)内一定有零点？

(教师运用“问题导学”，让学生经过火热的思考，水到渠成地获得了函数零点存在定理.)

问题6 请举例回答如下问题：

(1)若函数f(x)在区间[a，b]上的图象是一条连续不断的曲线，且满足f(a)·f(b)>0，则f(x)在(a,b)内有零点吗？

(2)若函数f(x)在区间[a，b]上的图象是一条连续不断的曲线，且满足f(a)·f(b)<0，函数f(x)在(a,b)内是否只有一个零点？

(3)若函数f(x)在区间[a，b]上的图象是一条连续不断的曲线，且满足f(a)·f(b)<0，还需满足什么条件时，函数f(x)在区间(a,b)内恰有一个零点？

(4)若函数f(x)在区间[a，b]上的图象是一条连续不断的曲线，且在区间(a,b)内恰有一个零点.是否必有f(a)·f(b)<0？

教师从“温度曲线”这一生活常识出发，让学生直观感受某个时间段上温度的变化，“区间”、“连续不断”、“异号”等要素一应俱全，为学生提供了探究性学习的好素材.通过设计环环相扣的“问题”引导学生探究，使学习过程成为在教师引领下“再创造”的过程，真正实现了“教教材”到“用教材教”.课堂灵动充溢，顺理成章地归纳、抽象、概括出问题的本质属性，生成了“函数零点存在定理”，提升了学生的直观想象、数学抽象、逻辑推理等核心素养.

2 善待错误资源，在辨析中生成

教师在课堂教学中“有意”或“无意”的“错误”，学生认知过程中的偏差或失误，我们称之为教学中的“错误资源”.由于学生的知识水平、思维方式等方面都存在着差异，课堂生成难免存在一定的偏颇与缺陷.教师应树立正确的“错误”观，并有效利用学生的错误，引导学生质疑、讨论，促使学生通过比较、分析、反思，不断深化知识学习，完善认知结构，提高对错误的“免疫力”.

案例2高中数学新教材人教A版必修第一册“基本不等式的应用”教学片断

对于上述错解，若不加以详细分析就将其束之高阁，必然会挫伤学生的自信心.因此教师因势利导，引导学生从失败走向成功.

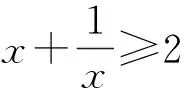
解决了以上问题之后,教师围绕问题特征引导学生进一步探究.

多好的生成性资源啊！在课堂教学中，教师应善于利用“错误资源”，探寻错误背后所隐含的教育价值，使之成为新的教学契机.通过互动交流，深度探究，促使学生在正确与错误的矛盾中碰撞，引发知错、改错、防错的良性反应，对数学学习产生积极的情感体验，并从中审视与体验，帮助学生建构起正确的认知结构，在“错误—发现—探究—归真”的良性循环中提升思维品质，涵育数学抽象、逻辑推理、数学建模、数学运算等核心素养.

3 引导反思评价，在感悟中生成

数学知识的学习过程既需要有一个对所学知识的掌握、加工与理解的认识过程，也需要有一个对该过程进行积极的监控、调节的反思过程.引导学生解后反思，对自己的思维过程进行再验证、再认识，在不断地提出问题又不断地解决问题的过程中，促使学生对数学思想方法从感性认识上升到理性认识，从而迸发思维的灵性，为演绎高效课堂、培养学生的关键能力创设良机.

(这是我校高三数学第一轮复习单元考试的一道填空题，题目不难，但错的很多.)

讲评课上，教师请一位答错的学生说说如何得出结果.

生1：由于函数f(x)为奇函数，因此f(0)=0，得lga=0，故a=1.

为了让学生从根本上认识错因，改正错误，教师引导学生反思：

反思1 求出a的值后，我们还应该考虑什么？

“这结果与已知条件矛盾！”学生一脸疑惑：“利用f(0)=0怎么会出错呢？”

教师不动声色，进一步引导学生反思：

反思2f(0)=0对所有奇函数都成立吗？若不是，请举出反例.

学生通过反思，体会到：由于函数f(x)中含有参数a，因此无法确定其定义域是否包含0.在未确定函数定义域是否含有0时，不能盲目应用f(0)=0求参数的值.

反思4 满足什么条件的函数才是奇函数呢？

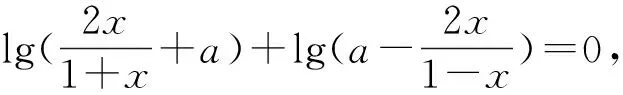
反思5 本题对今后解决这一类问题有什么启发呢？

生3：(1)解决函数问题应该优先考虑定义域，在a没有确定的情况下，无法确定x=0是否在定义域内；(2)判断函数的奇偶性用定义求解最可靠.

师：非常好！由以上解法我们还可以得到一个启示：对于等式恒成立问题，可以运用待定系数法求解参变量的值.

案例3中，教师利用学生的错解作为反面教材，引导学生进行反思，通过相互交流，深层思考.师生在互动对话中经历了从错误走向正确认识的过程，不仅加深了学生对概念内涵的认识，而且能促使学生的学习活动成为一种有目标有策略的主动行为，不断地发现问题，提出问题，生成新的问题的“生长点”，推动学生从浅层学习不断走向深度学习.

总之，只有合理、恰当地处理好预设与生成的关系，科学而艺术地把握动态生成资源，使之成为学生掌握知识、培养情感、提升能力的生长点，才能打造出基于学生主体的孕育数学核心素养的课堂教学.