极点极线背景下一组模拟题的求解及评析

湖南大学数学学院 (410082) 王少波 舒小保

极点极线的理论在《高等几何》[1]中有详细的介绍，高中很多圆锥曲线的相关结论(如定点、定值、斜率与角度等)在各类试题中多有体现.师生掌握一些极点极线的相关知识，将对试题的命制和解答大有帮助，本文例析一组模考题，供同仁参考.

1.极点极线的背景知识

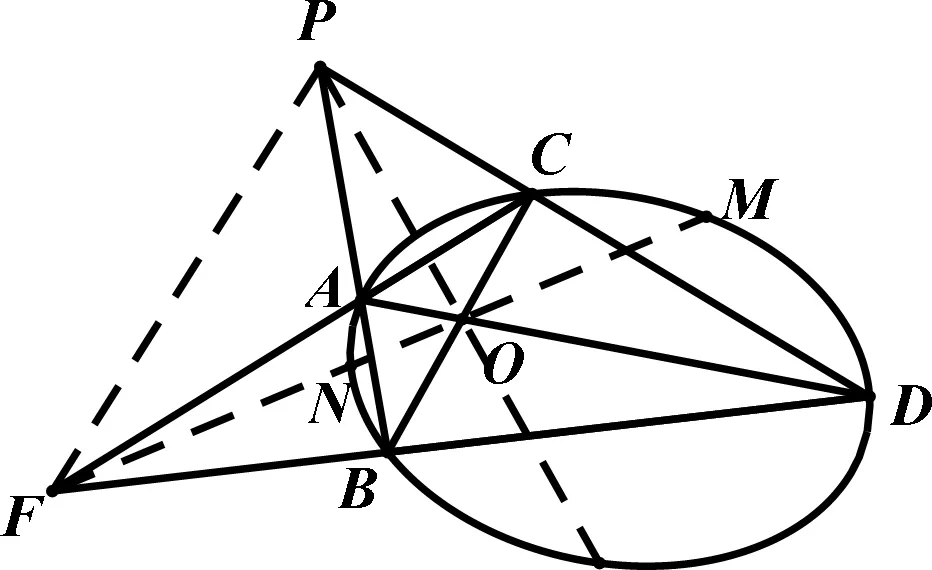
图1

(1)几何定义：如图1，过圆锥曲线外的一点P作两条直线交圆锥曲线于点A,B和C,D，连接BC和AD交于点O，AC和BD交于点F，连接FO交圆锥曲线于点N,M，则直线FO是点P的极线，点P是直线FO的极点，此时PM,PN恰好是圆锥曲线的两条切线.事实上，FO是点P关于椭圆的切点弦，P,F,O构成自极三点形，点F的极线是PO，点O的极线是PF.

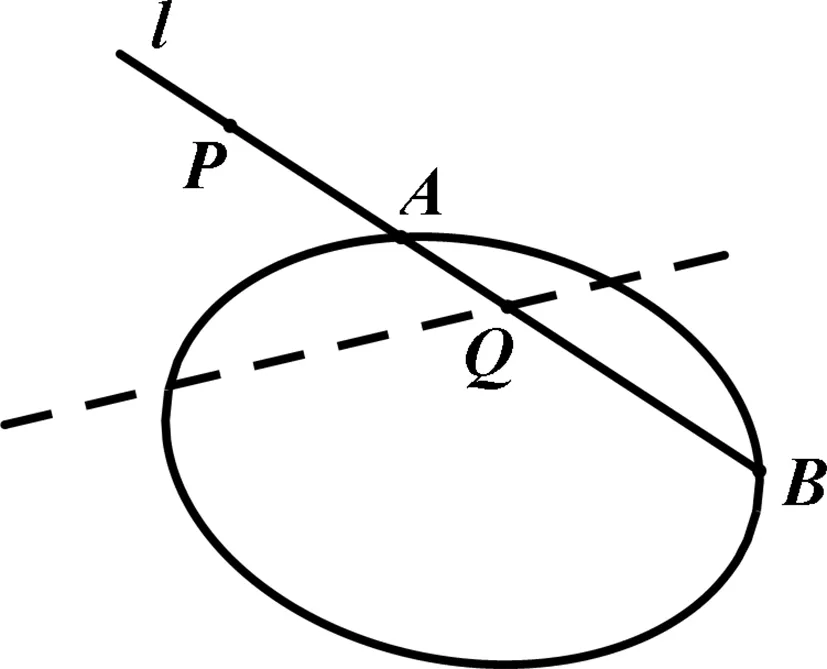
图2

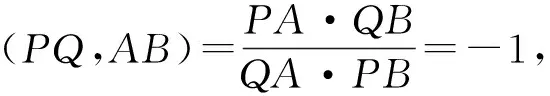
2.模拟题求解及评析

例1 (2021浙江强基联盟二模)已知F(0,1)且满足|PF|=x+1的动点P(x,y)的轨迹为C．

(1)求曲线C的轨迹方程；

(2)过点T(-1,0)的斜率大于零的直线与曲线C交于D，M两点，已知Q(1,-1)，直线DQ交曲线C于另外一点N，证明直线MN过定点．

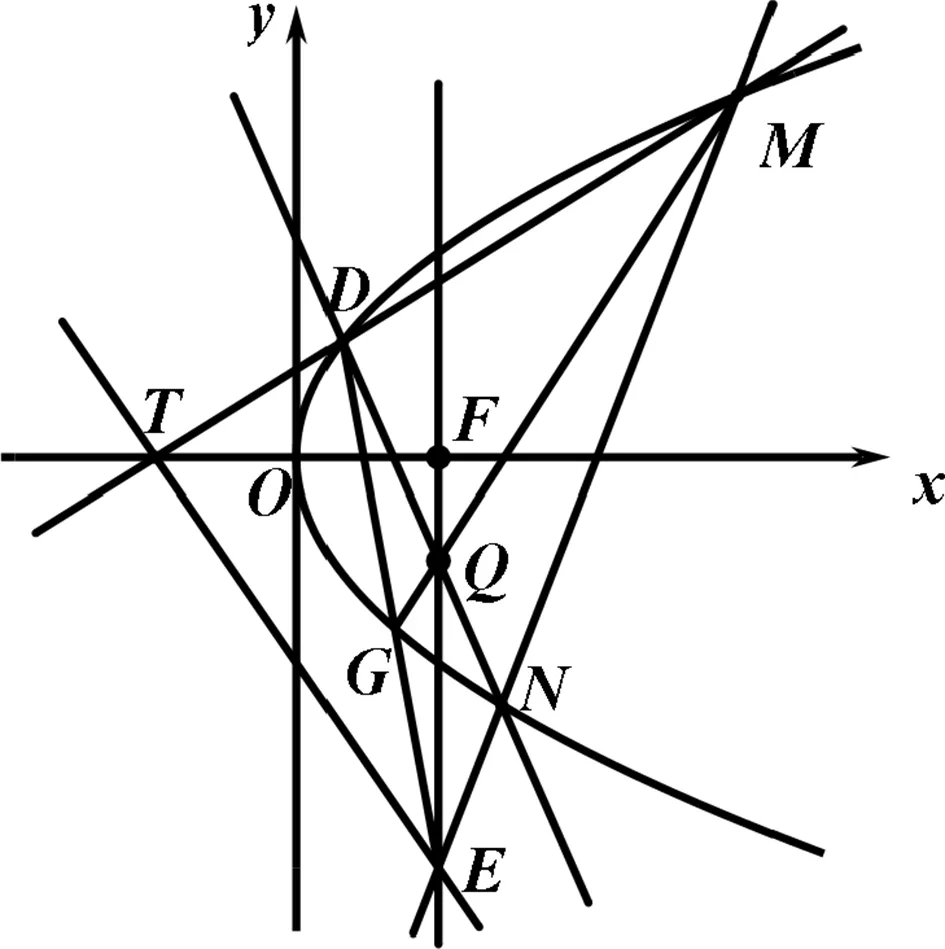
图3

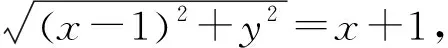
评析：本题的命题思路来自于极点极线的几何定义，特别是自极三点形的应用.本题还可以如下改编：连接MQ交曲线C于点G，试证明DG与MN交于一定点.

例2 (2021武汉模拟)已知抛物线C:x2=2y，设P为直线l:y=x-1上一点，过P作抛物线C的两条切线，切点分别为A、B.

(1)证明：动直线AB恒过定点Q；

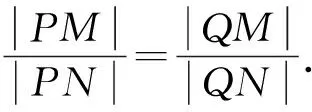
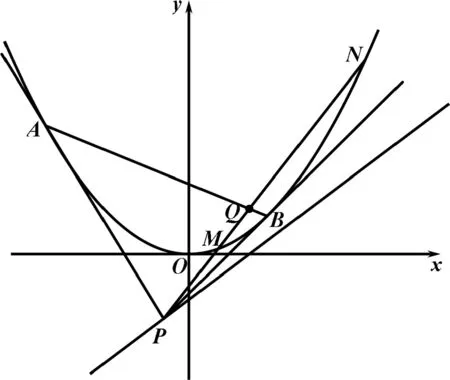
图4

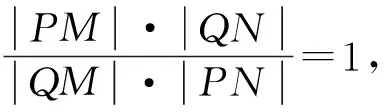
评析：本题涉及的极点极线背景知识有两个，一个是配极原则，一个是极点极线的代数定义.由上述解题过程可以看出，用极点极线知识解题更简洁，更容易高屋建瓴地看透问题的本质.

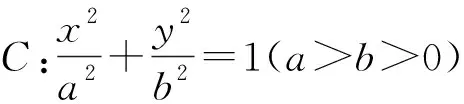
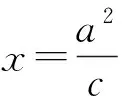
(2)设c=1，过定点(0,c)且斜率为k的直线l与椭圆C交于M，N两点，在y轴上是否存在一点Q，使得y轴始终平分∠MQN？若存在，求出Q点的坐标；若不存在，请说明理由．

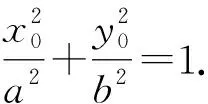
(2)如图5，若c=1，则定点为P(0,1),点P的极线y=3交y轴(对称轴)于点Q(0,3)，则有P、Q在y轴(对称轴)上且关于椭圆调和共轭，由极点极线的性质可知∠MQP=∠NQP,因此y轴始终平分∠MQN.

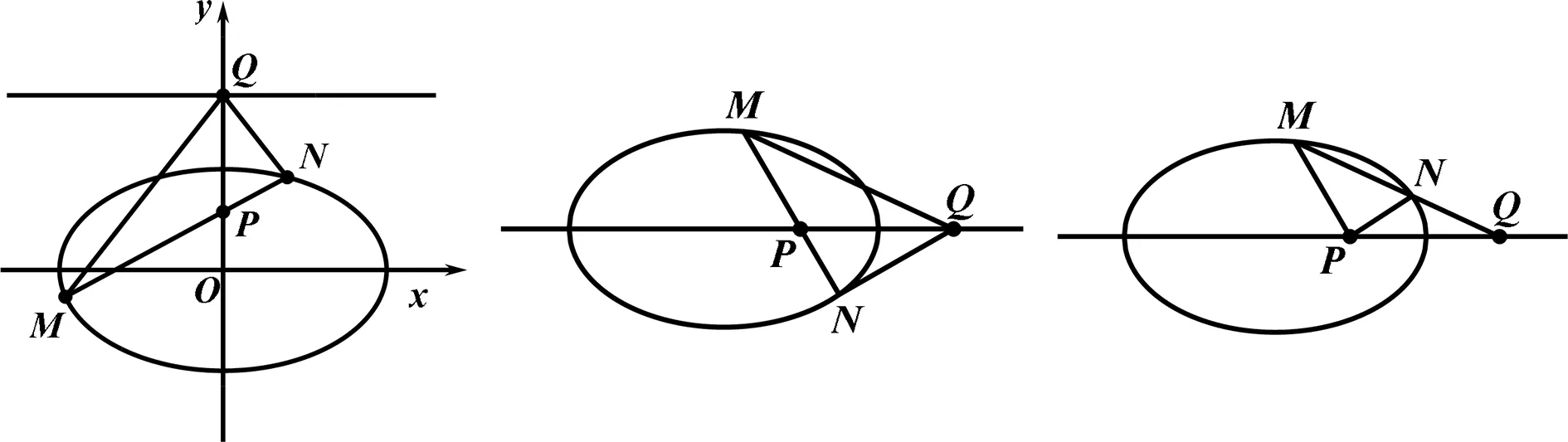
图5 图6 图7

评析：本题应用的是极点极线的如下性质[2]：圆锥曲线对称轴上的两点P、Q关于圆锥曲线成调和共轭,如图6、图7，过点P(或点Q)的直线交圆锥曲线于点M、N，则直线QM、QN(或直线PM、PN)与对称轴所成的夹角相等.此性质的逆命题也成立.

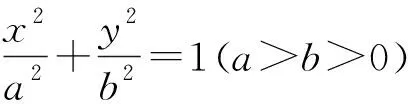
(1)求椭圆的方程；

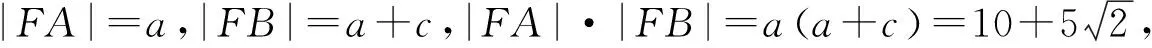
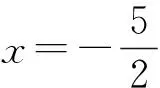
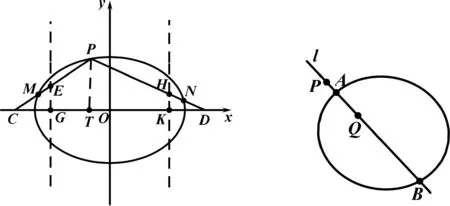
图8 图9

3.结语

以极点极线为背景的各类模拟题还有很多，在往年的高考题中也多有出现，以上评析了几个常用的极点极线性质的例题，以期能够起到抛砖引玉的作用，帮助教师与学生拓宽思维，对圆锥曲线的解题有所帮助.