交错层积竹板抗弯承载力计算方法
黄 明 刘文龙 刘 烨 丁 菡 吕清芳
(1 东南大学建筑设计研究院有限公司 南京 210096;2 东南大学土木工程学院 南京 211189;3 四川大学建筑与环境学院 深地科学与工程教育部重点实验室 成都 610065)
竹子是森林资源的重要组成部分,我国竹资源面积和质量均居世界首位[1-2]。竹材具有优良的力学性能,是一种高强度、低成本、环保低碳的绿色建材[3]。但原竹的物理性能不稳定、易干裂,工程竹在继承原竹优良特性的同时,克服了原竹几何不稳定性、质地不均匀、易虫蛀、耐久性差等缺点,得到了广泛的应用。
近年来,国内外学者对工程竹材以及竹复合材料的基本力学性能开展了大量研究[4-5]。王正等[6]、张礼平等[7]、蒋身学等[8]对竹材复合材的力学性能开展了研究,认为竹复合材是一种综合性能良好的建筑结构用材,具有较高的抗拉与抗压强度。肖岩等[9-12]开展了胶合竹材的力学性能试验,测量了胶合竹抗压、抗弯和抗剪强度以及弹性模量等指标,结果表明胶合竹材的主要力学性能满足建筑材料的要求。也有学者对竹构件的力学性能进行了深入研究,吕清芳等[13-15]对工程竹构件开展了试验研究,给出了建造房屋中竹质工程材料的强度和弹性模量的设计取值;Li 等[16]通过试验研究了15 种应力条件下工程竹板的力学性能和失效模式。已有的研究结果显示,大部分工程竹是各向异性材料,横纹方向和顺纹方向力学性能差异过大,构件受力性能与竹纤维的排布方向相关,而对于需要双向受力性能的材料,普通工程竹很难满足需求。
交错层积竹(CLB) 是由正交胶合木(CLT)材料演变而来、相邻两层竹层板垂直交错层积形成的板件,其克服了原竹和工程竹各向异性的性能缺陷,具有良好的双向受力性能,应用前景广阔[17]。目前关于CLB 构件的研究主要集中于CLB 构件的力学性能[17]和保温性能[18],而对于其抗弯承载力的设计规范与计算方法研究较少。因此,本文进行了2 组CLB 板四点弯曲试验,并采用正交胶合木构件的抗弯承载力计算方法计算了CLB 受弯构件的最大破坏拉应力,与试验所得结果进行对比,以期得出计算CLB 板抗弯承载力的适宜方法。
1 弯曲试验
1.1 试验过程
试验选用2 组(P20 和P12) 试件进行受弯性能试验,每组试件均加工5 个,共10 个试件。其中,P20 试件规格为长1 800 mm、宽600 mm、厚100 mm,由5 层竹层板胶合而成,每层竹层板厚度为20 mm;P12 试件规格为长1 800 mm、宽600 mm、厚60 mm,亦由5 层竹层板胶合而成,每层竹层板厚度为12 mm。竹材的顺纹抗拉弹性模量为17 949 MPa,抗弯弹性模量为15 094 MPa。试验加载直至试件破坏,测量试件的位移和应变。
1.2 试验结果
各试验板跨中的荷载—位移曲线如图1 所示。2 组试件各选取一个代表性试件绘制了荷载—应变曲线,如图2 所示,其中S-1、S-2、S-3、S-4、S-5、S-6 均为应变片,其中S-1、S-2、S-3位于CLB 板顶部,S-4、S-5、S-6 位于CLB 板底部,如图3 所示。

图1 各试验板的荷载—跨中位移曲线Fig.1 Load-mid-span displacement curves of panels

图2 试验板的荷载—应变曲线Fig.2 Load-strain curves of panels

图3 应变片布置图Fig.3 Layout drawing of strain gauges
可以看出,2 组CLB 板具有一致的破坏模式,最先破坏的点发生在CLB 板的底部,在加载点下方的顺纹竹纤维断裂,并迅速拉断上层横纹竹层板,裂缝沿着倒数第2 层与第3 层的界面发展至第3 层中间,第2 层的横纹竹层板同时断裂,最后顶部断裂,试件破坏。2 组CLB 板各选取一个代表性试件展示破坏情况,如图4 所示,故最大破坏拉应力出现在底部纯弯段处,各CLB 板的最大破坏拉应力由底部竹纤维的极限拉应变求出,如表1 所示。

表1 CLB 板各试件最大破坏拉应力Tab.1 Maximum failure tensile stress of CLB slabs

图4 CLB 板破坏形态Fig.4 Failure patterns of CLB panels
2 基于理论的CLB 抗弯构件承载力计算方法
由于尚未形成有关CLB 构件抗弯承载力计算的设计规范与方法,故参考《木结构设计规范》(GB50005-2017)[19]中的规定,通过公式(1) 计算CLB 构件的抗弯承载力:

公式 (1) 中:fm—抗弯强度设计值,N/mm2;M—弯矩设计值,N·mm2;Wn—净截面抵抗矩,mm3;El—顺纹弹性模量,N/mm2;EIeff—有效抗弯刚度,N·mm2;L—跨度,mm;h—截面高度,mm。
CLB 抗弯强度设计值应乘以组合系数kc(kc≤1.2,大于1.2 时取1.2):
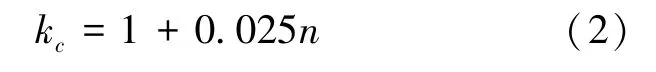
公式(2) 中:n—最外侧层板数量。
本文中的CLB 板,跨度L均大于10h,根据公式(1) 可得最大破坏拉应力(σmax) 为:

公式 (3) 中:ht ot为竹板构件的截面高度,mm。
根据公式(3) 可知,CLB 构件抗弯承载力计算的关键在于计算有效抗弯刚度。本文分别选用《木结构设计规范》、机械连接梁理论和复合理论,参考正交胶合木受弯构件的有效抗弯刚度计算方法以计算交错层积竹受弯构件的有效抗弯刚度,并将根据有效抗弯刚度计算的最大破坏拉应力计算结果与试验结果进行对比。
2.1 《木结构设计规范》 中规定的计算方法
根据《木结构设计规范》 中的规定,宜根据各层木板的强度设计值按线弹性理论进行计算正交胶合木的有效抗弯刚度。由于横纹层板作为非刚性连接对顺纹层板的刚度有折减,横纹方向层板的刚度与纵纹方向层板的刚度的折减抵消,故计算CLB板有效抗弯刚度EIeff时,仅考虑顺纹层板。CLB 构件的有效抗弯刚度EIeff应按式(4) 计算。

公式(4)中:Ei—弹性模量,N/mm2;Ii—层板截面惯性矩,mm4;Ai—层板截面面积,mm2;b—构件截面宽度,mm;ti—层板厚度,mm;n—顺纹板的层数;ei—第i层顺纹板的偏心距,mm。
2.2 机械连接梁理论
2.2.1 理论修正
机械连接梁理论(Gamma Method)[20]最初是为与机械紧固件连接的工字梁或T 字梁所提出的。根据机械连梁理论,有效抗弯刚度(EIeff) 由梁的连接效率系数γ决定。连接效率系数γ取决于紧固件的滑移特性(s/K),s为机械紧固件之间的距离,K为机械紧固件的滑移模量[21]。
由于CLB 板为层板胶合而成,无机械连接,因此需要修正该理论才能适用于CLB 板。假设CLB 板中只考虑顺纹层板承担荷载,横纹层板仅考虑其连接作用,即CLB 板的顺纹层板被视为与“机械紧固件”连接的“梁”,而横纹层板被视为假想的“机械紧固件”。故紧固件的滑移特性修正为公式(5),根据公式(6) 来确定连接效率系数γ:

连接效率系数γ的取值范围为:0<γ<1 (γ=1 时为刚性连接,γ=0 时为无连接)。
2.2.2 计算方法
有效抗弯刚度EIeff根据公式(7) 计算。

公式(7) 中:αi—第i层顺纹层板的偏心距,mm。
2.3 复合理论
2.3.1 基本假设
复合理论(K Method)[20]是胶合板工业中广泛应用的设计理论。根据该理论,在计算弯曲性能时忽略横向层板的刚度,即E90=0。对于CLB板,在计算有效抗弯刚度(EIeff) 时需对该理论进行修正,并提出以下假设:
1) 线性应力应变关系;
2) 横向层板刚度:E90=E0/30;
3) 平截面假定;
4) 忽略剪切变形。
2.3.2 基于复合理论的CLB 板有效抗弯刚度计算方法
基于复合理论的CLB 板有效抗弯刚度EIeff可由公式(8) 得出:
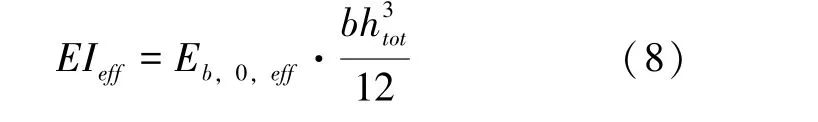
公式(8) 中:htot为CLB 板的截面高度,单位mm;Eb,0,eff为有效刚度,根据表2 计算;k为影响因子,根据表3 计算,αm为位于截面中间的m层单板的厚度。

表2 CLB 板有效强度和有效刚度计算公式Tab.2 Calculating formulas of Effective strength and effective stiffness for CLB

表3 不同工况条件下k 的计算公式Tab.3 Calculating formulas of k under different conditions

表3 (续)
3 基于理论的CLB 抗弯构件承载力计算结果
基于上述3 种理论,计算CLB 板的有效抗弯刚度EIeff,根据公式(3) 计算出CLB 板的最大破坏拉应力(σmax),对比计算值与试验所得值,分析CLB 板的计算方法是否适用。
3.1 基于《木结构设计规范》 的计算结果
3.1.1 计算公式及参数
根据公式(4) 计算出有效抗弯刚度EIeff,再根据公式(3) 计算最大破坏拉应力σmax,所需参数见表4。其中:M=1/6PL,P限承载力。同理可计算出P12 板的最大破坏拉应力σmax。

表4 CLB 板P20 有效抗弯刚度和最大破坏拉应力基于《木结构设计规范》 的计算参数Tab.4 Calculation parameters of effective flexural stiffness and maximum failure tensile stress of CLB slab P20 based on Wood structure design code
3.1.2 理论计算结果与试验结果比较
对比参考《木结构设计规范》 的计算结果与试验所得结果,对比结果如表5 所示。可以看出,大部分试验板和平均值误差误差均在10%以内。

表5 基于《木结构设计规范》 的最大拉应力计算结果与试验结果比较Tab.5 Comparison of the maximum tensile stress between the calculated results based on Wood structure design code and the test results
3.2 基于机械连接梁理论的计算结果
3.2.1 计算方法
根据公式(6) 计算连接效率系数γ,连接效率系数γ计算简图如图5 所示。

图5 连接效率系数γ 计算简图Fig.5 Simple calculation diagram of γ
根据公式(7) 可计算出有效抗弯刚度EIeff,再根据公式(3) 计算最大破坏拉应力σmax,所需参数见表6。其中:M=1/6PL,P极限承载力。同理可计算出P12 板的最大破坏拉应力σmax。

表6 CLB 板P20 有效抗弯刚度和最大破坏拉应力基于机械连接梁理论的计算参数Tab.6 Calculation parameters of effective flexural stiffness and maximum failure tensile stress of CLB slab P20 based on Gamma Method
3.2.2 理论计算结果与实际试验结果比较
对比机械连接梁理论计算得出的最大破坏拉应力与试验所得结果,对比结果如表7 所示。可见,大部分试验板和平均值误差误差均在10%以内。

表7 基于机械连接梁理论的最大拉应力计算结果与试验结果比较Tab.7 Comparison of the maximum tensile stress between the calculated results based on Gamma Method and the test results
3.3 基于复合理论的计算方法
3.3.1 计算公式及参数
根据表2 和表3 可知:

根据公式(8) 可计算出有效抗弯刚度EIeff,再根据公式(3) 计算最大破坏拉应力σmax,所需参数见表8。其中:M=1/6PL,P为极限承载力。同理可计算出P12 板的最大破坏拉应力σmax。

表8 CLB 板P20 有效抗弯刚度和最大破坏拉应力基于复合理论的计算参数Tab.8 Calculation parameters of effective flexural stiffness and maximum failure tensile stress of CLB slab P20 based on K Method
3.3.2 理论计算结果与实际试验结果比较
对比参考复合理论计算得出的最大破坏拉应力与试验所得结果,对比如表9 所示。根据表9对比结果,大部分试验板和平均值误差误差均在10%以内。

表9 基于复合理论的最大拉应力计算结果与试验结果比较Tab.9 Comparison of the maximum tensile stress between the calculated results based on K Method and the test results
3.4 基于3 种理论的最大拉应力计算结果对比
对比上述3 种理论计算得出的CLB 板的最大破坏拉应力结果(表10) 可以看出,基于3 种理论的计算结果与实际试验结果的误差均小于10%,其中基于《木结构设计规范》 中规定的方法和基于复合理论的计算结果与实际试验结果的误差均小于5%。基于机械连接梁理论的误差大于另2 个理论,原因是机械连接梁理论仅考虑CLB 板中顺纹层板的刚度,忽略了横纹层板的刚度,导致误差较大;而基于《木结构设计规范》 的计算方法,将横纹层板作为非刚性连接和横纹层板本身的刚度进行抵消,计算得出的有效抗弯刚度EIeff更加接近真实值;基于复合理论的计算方法,利用复合影响因子K,同时考虑横纹层板的连接特性和横纹层板本身的刚度,计算结果较为准确。

表10 基于3 种理论的最大拉应力计算结果与试验结果比较Tab.10 Comparison of the maximum tensile stress between the calculated results based on three theories and the test results
4 结论
基于《木结构设计规范》、机械连接梁理论和复合理论,参考正交胶合木受弯构件的抗弯承载力计算方法,计算了交错层积竹受弯构件的最大破坏拉应力,并进行了2 组CLB 板受弯性能试验,通过分析试验结果并与理论计算结果比较,得出以下结论。
1) 2 种规格的CLB 板具有基本一致的破坏模式。CLB 板底部在加载点附近的纤维由于达到极限拉应变而首先断裂,并拉断底部第2 层横纹竹层板,裂缝沿着倒数第2 层与第3 层的截面发展至第3 层中间,第2 层的横纹竹层板同时断裂,最后顶部断裂,试件破坏。
2) 基于机械连接梁理论的计算方法由于忽略横纹层板本身的刚度,计算出的CLB 板的最大破坏拉应力与试验所得结果的误差稍大于另2 个理论;基于《木结构设计规范》 和复合理论计算出的CLB 板最大破坏拉应力与实际试验结果的误差均小于5%,可以用作CLB 板抗弯承载力的计算方法。

