毛白杨静态压缩力学性能研究及吸能分析
谢若泽,郭玲梅,李尚昆,张斌,钟卫洲
(1.中国工程物理研究院总体工程研究所,四川 绵阳 621900;2.工程材料与结构冲击振动四川省重点实验室,四川 绵阳 621900)
各类工业产品,特别是武器装备,在全寿命周期中,有可能经历异常环境,遭遇意外事故,需要采取各种措施对产品进行有效保护,而包装箱就是最常用的措施之一。在异常环境下包装箱的性能如何,对产品的安全性和效能的有效发挥起着很大的作用[1-4]。
木材由于具有取材方便、易加工、高比吸能、耐冲击、阻燃隔热等优良特性,目前已作为结构材料广泛应用于工业产品和民用建筑领域。同时由于木材具有较好的吸能特性,常在各类包装箱中作为缓冲材料。
包装结构及其内容物经历的异常环境通常包含火烧、水浸、跌落以及穿击等,这就要求抗事故包装结构不仅耐高温、防火、隔热,同时要具有承载、抗冲击等性能。木材作为包装结构的重要组成部分,其力学性能和吸能特性日益受到人们的关注。
木材为天然生长材料,其纤维组织沿生长方向为顺纹,沿横截面方向又有横纹径向和横纹弦向2个方向,不同的方向具有不同的力学特性。木材的力学性能受含水率和应变率的影响较大,在小变形时可视作线弹性材料,而在较大载荷时,其力学行为表现为非线性。
学者们针对木材的力学性能进行了大量研究。Reiterer等[5]研究了木材沿顺纹、径向的单轴压缩性能,采用正交各向异性弹性和Tsai-Hill强度理论描述了不同方向的杨氏模量、泊松比和压缩强度。Koji、Kazunari、Mika等[6-8]针对哑铃状木材试样开展了拉伸实验,表明木材的拉伸强度与材料方向密切相关,垂直于木材纤维方向的拉伸强度相对较低,即木材胞元间的黏结强度小于木材纤维顺纹拉伸强度。W.Sonderegger等[9]通过准静态弯曲实验、冲击弯曲实验和拉伸实验获得了云杉在不同力学状态下的破坏强度。钟卫洲等[10]利用Instron和Hopkinson压杆对含水率12.72%的云杉木材进行了准静态和动态压缩实验,获得了云杉木材沿顺纹、横纹径向和横纹弦向3个方向的抗压模量、准静态下应力应变曲线和3种应变率下的动态应力应变曲线。姚胜等[11]针对3种不同树龄的速生杨木材,测试了它们的物理力学性质,分析了树种和树龄对木材物理力学性能的影响。有关含水率对材料性能的影响、微观结构对材料性能的影响以及失效机制等,也有很多研究者进行了研究[12-14]。
毛白杨是我国主要的人工林树种,其木材材质、颜色均匀,湿心材比例低,加工性能好,是重要的防护林树种、城市绿化树种和风景景观树种,同时也是我国重要的用材林树种,可用于包装运输、建筑结构等。黄荣风、毛安等[15-16]研究了热处理对毛白杨物理性能的影响,而作为缓冲材料,从力学和吸能角度对毛白杨木材性能的研究则很少看到。文中测试了毛白杨的密度和含水率等物理参数,并利用Instron试验机对毛白杨木材试件沿顺纹、横纹径向和横纹弦向进行准静态压缩实验,获得了毛白杨木材3个方向的抗压模量、准静态压缩应力-应变曲线,分析了毛白杨木材的吸能特性。
1 试件取材
木材的纤维组织沿树干方向生长,并向四周发散,具有正交各向异性。在树干内部垂直于树干方向和年轮方向截取一个立方体,则该立方体具有3个方向。平行于树干方向为顺纹方向;垂直于树干方向并平行于树干直径的为横纹径向;垂直于树干方向并平行于年轮方向的为横纹弦向。试样取向如图1所示[10]。

图1 试件取向示意Fig.1 Directional scheme of specimen
毛白杨采自湖北省利川市,均为直径为400 mm的圆木,所有试件取材均在髓心以外进行。经实验测得的毛白杨木材试件的平均密度[17](烘干前)为0.544 g/cm3,经温度为(103±2) ℃的烘箱烘烤10 h后,得到的平均含水率[18]为14.6%。
2 毛白杨弹性模量
测量毛白杨弹性模量所用试件的尺寸为60 mm×20 mm×20 mm,共15件,试件的长度方向分别沿横纹径向、横纹弦向和顺纹方向,每个方向5件[19-22]。毛白杨弹性压缩实验所获得的3个方向测试曲线分别如图2(顺纹)、图3(横纹径向)、图4(横纹弦向)所示。针对测试曲线的弹性段进行直线拟合,获得了毛白杨的顺纹抗压弹性模量、横纹径向抗压弹性模量、横纹弦向抗压弹性模量,分别为10.49 GPa、887和504 MPa。由此可知,毛白杨不同方向的抗压弹性模量从大到小依次为顺纹方向、横纹径向、横纹弦向,横纹径向抗压弹性模量约为顺纹的0.083,横纹弦向抗压弹性模量则为顺纹的0.048。
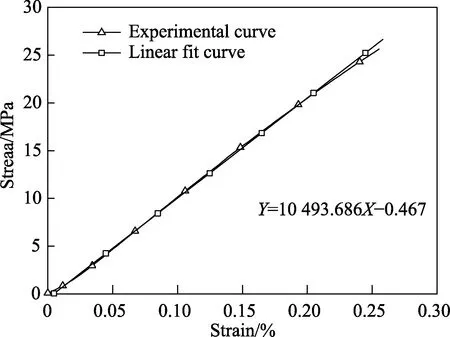
图2 顺纹抗压弹性模量实验测试与拟合曲线Fig.2 Axial elastic modulus
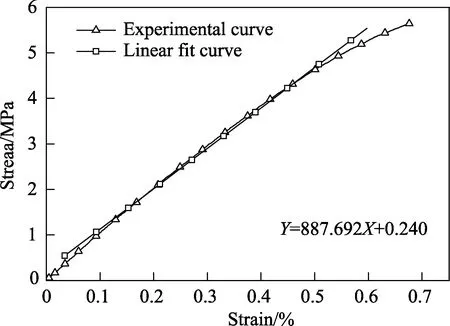
图3 横纹径向抗压弹性模量实验测试与拟合曲线Fig.3 Radial elastic modulus
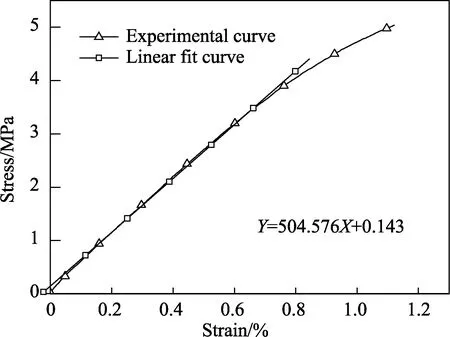
图4 横纹弦向抗压弹性模量实验测试与拟合曲线Fig.4 Tangential elastic modulus
3 静态力学性能
毛白杨准静态压缩实验所用试件的尺寸为30 mm×20 mm×20 mm,试件的长度方向分别沿横纹径向、横纹弦向和顺纹方向[19-22],加载方向沿试件长度方向。准静态压缩作用下,毛白杨沿3个方向的应力-应变曲线如图5所示。由图5可见,毛白杨木材的压缩加载过程可以分为弹性、屈服、压实3个阶段。
顺纹方向准静态压缩应力-应变曲线如图5a所示,材料进入塑性屈服时的应变约为0.025,屈服应力约为42.4 MPa。当应变达到约0.6时,材料进入压实状态,应力-应变曲线快速上升。整个曲线多次振荡,而不是圆滑的曲线,说明压缩过程中材料的承载能力随着胞壁结构的渐进破坏出现一定的波动。实验后试件的破坏情况如图6所示,可见毛白杨木材纤维中部在顺纹压缩作用下发生屈曲折断,然后向四周伸张、卷曲。受加载头和底部支撑面摩擦作用,沿纤维方向中部位置发生脱层,端面出现明显纤维脱层现象较少。
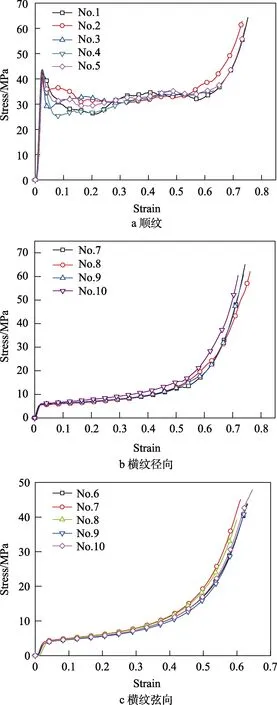
图5 不同压缩方向应力-应变曲线Fig.5 Stress-strain curves of different directions: a) axial; b) radial; c) tangential

图6 顺纹压缩变形情况Fig.6 Deformation after axial compression
横纹径向压缩的应力-应变曲线如图5b所示。不同于顺纹方向,在准静态横纹径向压缩过程中,应力-应变曲线没有先上升、后下降反复振荡的过程,而是呈单调递增。材料进入塑性屈服时的应变约为0.02,屈服应力约为5.81 MPa。在进入屈服以后,应力-应变曲线进入一个平台区,应力随着应变的增加而缓慢增长。当应变达到约0.55时,木材胞壁发生破坏压实,应力进入一个快速增长阶段。实验后的破坏情况如图7所示。在横纹径向压缩作用下,毛白杨试件出现褶皱,且每层褶皱与加载面平行,并向侧面膨出。试件的轴线变成曲线,且试件的侧面成为波浪型,并沿径向产生劈裂。

图7 横纹径向压缩变形情况Fig.7 Deformation after radial compression
横纹弦向压缩应力-应变曲线如图5c所示。与准静态横纹径向压缩相似,在准静态横纹弦向压缩过程中,应力-应变曲线没有先上升、后下降反复振荡的过程,而是呈单调递增。材料进入塑性屈服时的应变约为0.02,屈服应力约为3.26 MPa。在进入屈服以后,应力-应变曲线进入一个平台区,应力随着应变的增加而缓慢增长。当应变达到约0.45时,木材胞壁发生破坏,试件进入压实阶段,应力进入一个快速增长阶段。压缩后的试件破坏情况如图8所示,可见试件沿压缩侧向(即径向)发生侧弯,部分试件沿年轮发生分层,最终形成剥离。

图8 横纹弦向压缩变形情况Fig.8 Deformation after tangential compression
毛白杨沿顺纹方向、横纹径向和横纹弦向的压缩应力-应变曲线比较如图9所示。顺纹方向的初始压缩强度远高于横纹(径向和弦向)。对于顺纹方向压缩,试件具有初始压缩强度42.4 MPa,而横纹径向的屈服强度约为5.81 MPa,横纹弦向的准静态屈服强度约为3.26 MPa。不同压缩方向应力-应变曲线中,横纹径向和横纹弦向的应力-应变关系呈单调递增,而顺纹方向的应力-应变关系则分为增加—减小—平台—快速增加4个阶段。
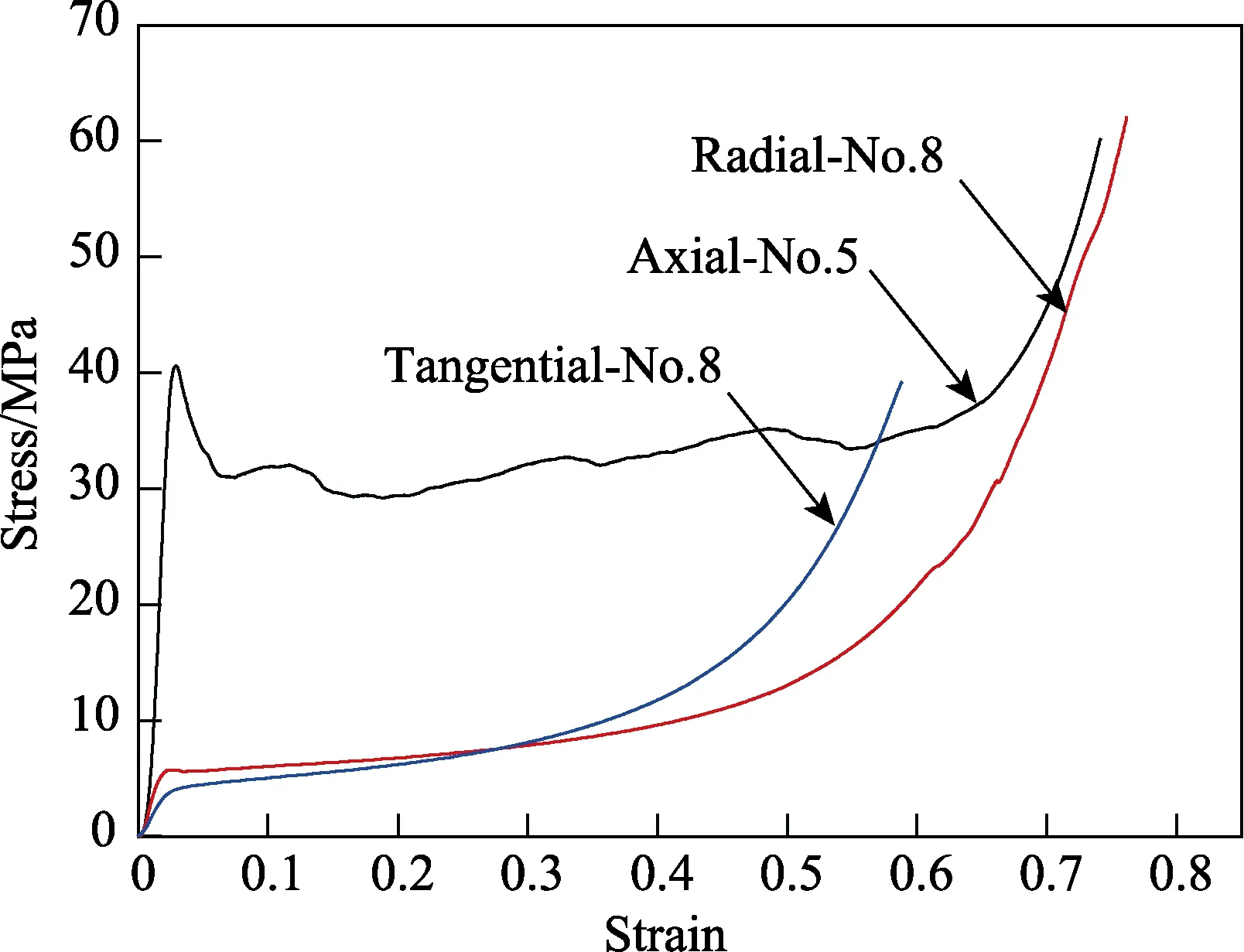
图9 不同方向的应力-应变曲线比较Fig.9 Comparison of stress-strain curves in different directions
4 不同方向准静态压缩吸能分析
对于材料的吸能,一般通过应力-应变关系计算得到,如式(1)所示。

对于多孔泡沫材料的吸能评估,Miltz等人[23]根据缓冲材料准静态压缩应力-应变曲线,提出了吸能率E(Energy Absorption Efficiency)和理想吸能率I(Ideality Energy Absorption Efficiency)来描述材料的吸能特性。其相应的数学表达式见式(2)和式(3)。

式中:σm和εm分别为某位置所对应的应力和应变。式(2)表明,吸能效率为缓冲材料所吸收的能量与所对应应力的比值;式(3)表明,理想吸能效率为缓冲材料所吸收的能量与理想吸能材料(屈服平台区为矩形,应力为恒值)吸能的比值。
由于木材为多胞材料,可采用式(2)与式(3)对毛白杨不同方向(顺纹、横纹径向和横纹弦向)准静态压缩吸能特性进行分析。按式(1)计算得到的毛白杨单位体积不同方向压缩下的吸能-应变曲线如图10所示。可以看出,沿不同方向压缩得到的毛白杨木材单位体积吸能随工程应变的增加而增大。在相同变形(应变相等)情况下,沿顺纹方向压缩吸收的能量最大。在应变小于0.45情况下,横纹径向和弦向压缩吸能曲线基本重合。随着应变继续增加,横纹弦向的压缩吸能略大于横纹径向。
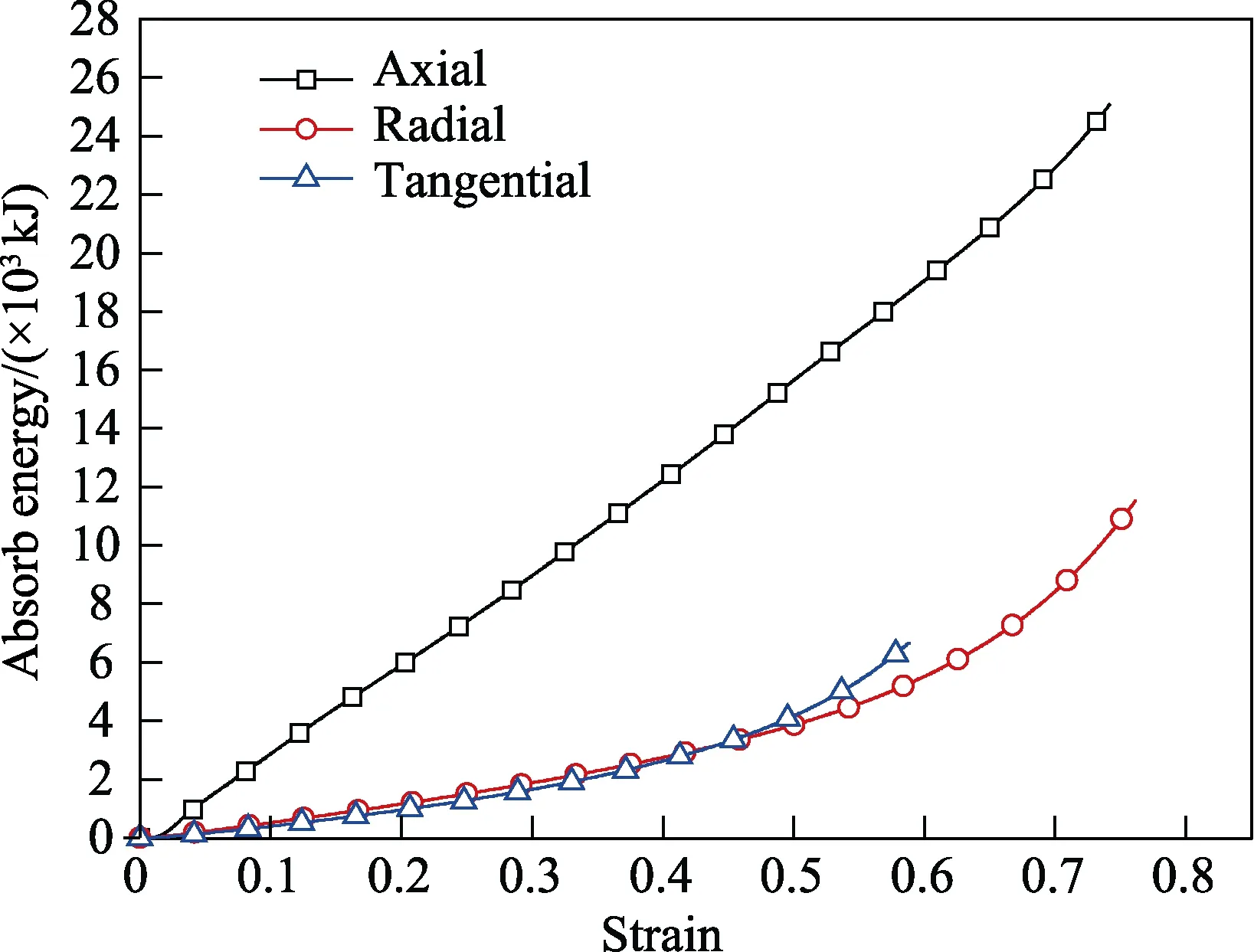
图10 不同方向压缩吸能-应变关系Fig.10 Absorbing energy-strain curves of different compression directions
根据式(2)计算得到的毛白杨不同方向吸能率与应变关系如图11所示。可以看出,在应变小于0.1时,不同方向压缩能量吸收率差异不大,吸能率曲线基本重合。随着应变继续增加,顺纹方向吸能率最大,横纹弦向吸能率最小。

图11 不同方向吸能率-应变关系Fig.11 Energy absorption efficiency-strain curves of different compression directions
依据理想吸能率式(3)计算获得的毛白杨理想吸能率与应变关系如图12所示。由于毛白杨顺纹压缩应力-应变关系非单调性,按式(3)计算得到的毛白杨顺纹压缩平台段理想吸能率超过1.0。由图12可知,在应变范围很小时(应变小于0.054),3个方向的理想吸能率首先快速下降,然后快速上升。当应变大于0.054以后,顺纹压缩理想吸能率最高,横纹弦向的理想吸能率最低。
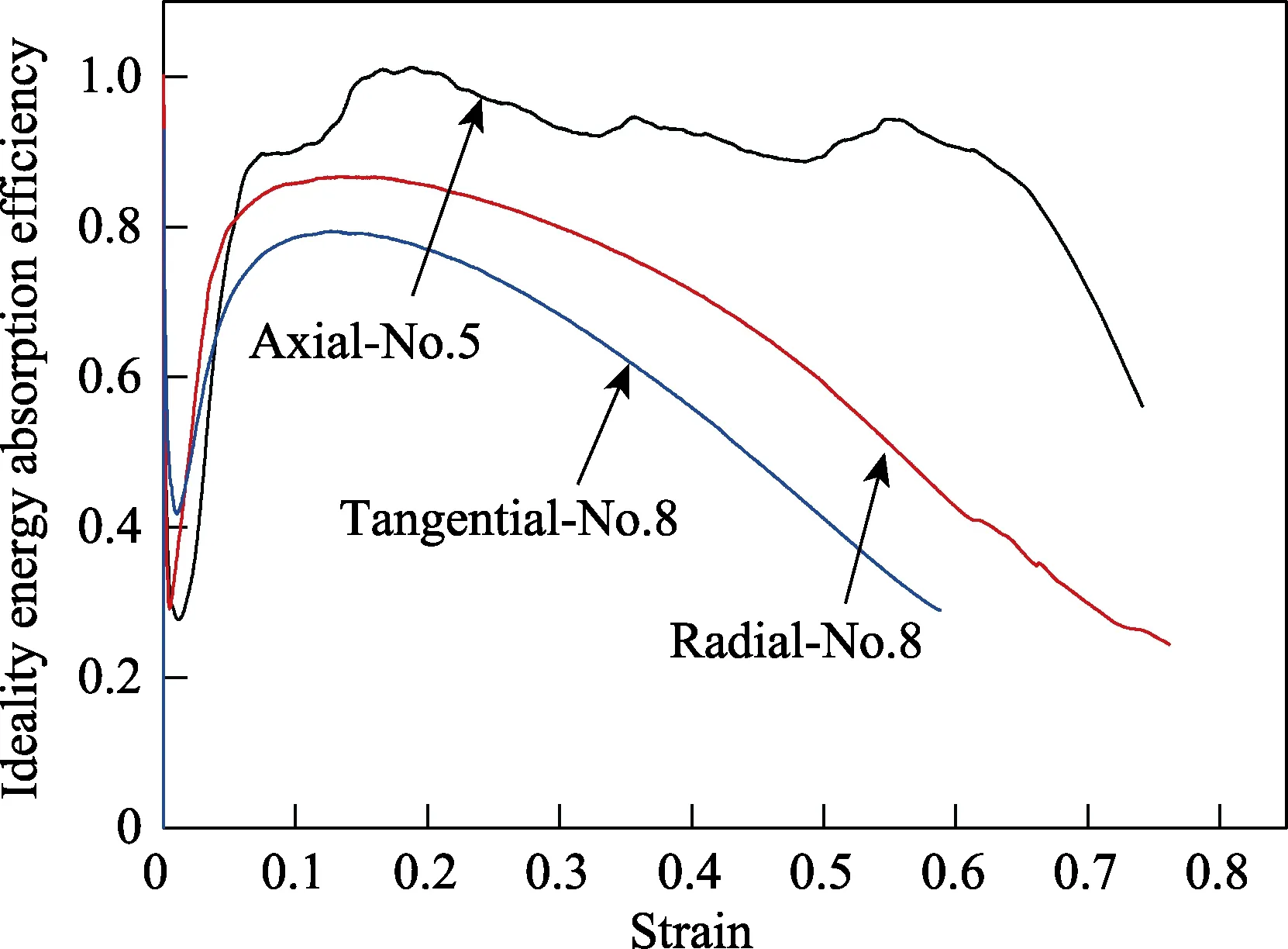
图12 不同方向理想吸能率-应变关系Fig.12 Ideality energy absorption efficiency-strain curves of different compression directions
从上述分析看出,毛白杨不同方向压缩屈服强度不同,其中顺纹方向压缩强度最大(约42.4 MPa),而横纹径向的屈服强度约为5.81 MPa,横纹弦向的准静态屈服强度约为3.26 MPa。横纹径向与横纹弦向方向压缩吸能率、理想吸能率与应变关系基本一致。由于顺纹压缩应力-应变关系非单调性,其压缩吸能率接近0.5,理想吸能率达到约1.0。因此将毛白杨作为包装缓冲材料时,需针对被保护体所能承受的变形及应力范围来合理确定木材放置方向,充分利用木材塑性屈服变形耗散能量,以此起到有效保护产品的作用。
5 结论
针对含水率为14.6%,密度为0.544 g/cm3的毛白杨木材试件进行了静态压缩力学性能实验,获得了毛白杨顺纹、横纹径向和横纹弦向的抗压模量、准静态压缩应力-应变曲线,并对其不同方向的吸能特性进行了分析,得到如下结论。
1)毛白杨木材顺纹、横纹径向和横纹弦向的抗压弹性模量分别为10.49 GPa、887和504 MPa。
2)顺纹方向压缩屈服应力约为42.4 MPa,横纹径向压缩屈服应力约为5.81 MPa,横纹弦向压缩屈服应力约为3.26 MPa。
3)顺纹方向加载时,毛白杨的破坏模式表现为试件轴向屈曲,木材纤维折断;横纹径向的静态破坏模式为沿径向的裂纹及破坏;横纹弦向的静态破坏模式为沿木纹方向的分离破坏。
4)在相同变形(应变相等)情况下,毛白杨木材沿顺纹方向压缩单位体积吸能最大。在应变小于0.45情况下,横纹径向和弦向压缩吸能曲线基本重合。随着应变继续增加,横纹弦向压缩吸能略大于横纹径向压缩吸能。
5)对于准静态压缩作用下,在应变小于0.1时,不同方向的压缩能量吸收率差异不大,吸能率曲线基本重合。随着应变继续增加,顺纹方向吸能率最大,横纹弦向吸能率最小。

