基于向量机的计算机视觉在钢材分类缺陷检测中的应用*
李 锋
(广东交通职业技术学院信息学院,广州 510650)
1 引言
在传统钢材生产中,传统人工检测存在着速度慢、检测标准不统一、检测成本过高等问题。随着智能制造的发展,基于计算机视觉的缺陷检测技术得以兴起并被广泛应用。在实际生产中,钢材表面缺陷检测是衡量质量的重要因素,业界急需更高精度的检测缺陷算法[1]。当前工业界已有很多缺陷检测的相关研究,其中大多数都是基于计算机视觉采集系统完成对图像采集工作,并通过相关技术将缺陷识别检测出来,最后通过图像分析将缺陷进行分类。对于这类技术的应用,在工业界并未得到广泛的推广使用,且分类精度有待提高。
支持向量机在小样本条件下有其自身优势,比如:较强的学习泛化能力、对高维度的识别能力以及有着最低的结构化风险等,能确保实现较为理想的缺陷检测识别率[2-3]。
2 支持向量机基本原理
支持向量机(Support Vector Machine,SVM)算法是Vapnik 等人在统计学习基础上提出的,其核心是让结构化风险最小化,它适于小样本量与高维度,并具有泛化能力强、推广能力强、全局最优等特点。SVM 能在低维非线性模式下转化为线性可分情况,降低运算复杂度,具有良好泛化能力和鲁棒性[4]。在实际数据中,有线性可分与线性不可分两种情况,对此,支持向量机也分为线性支持向量机及非线性支持向量机。而核函数的引入成功解决了非线性可分的问题。
2.1 线性支持向量机
线性支持向量机的原理图见图1。假设给定一个特征空间上的训练数据集T={(x1,y1),(x2,y2),...,(xN,yN)},其中xi∈Rn,yi∈[-1,垣1],i=1,2,...,N。xi为第i个特征向量,yi为类标记,当它等于垣1 时为正例;为-1 时为负例。
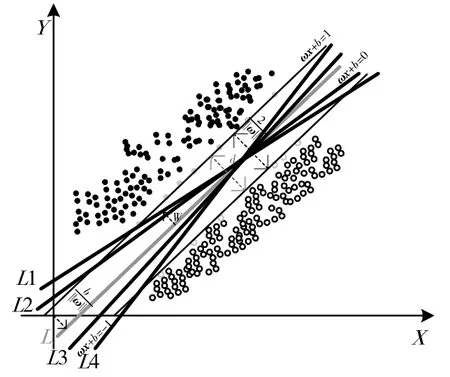
图1 线性支持向量机

其中,yi(ωxi垣b)≥1,0≤αi≤C,i=1,2,...,N;yi是样本相应的输出值,对于φ(ω)存在有唯一极小值。利用朗格拉日乘子法,将优化分类问题转为对偶问题:,其中αi≥0,i=1,2,...,m,且
优化到分类超平面,有:

式中,αi*是朗格拉日乘子,b*=yi-,为保证间隔最大化及误差率最小,引入惩罚因子D。最终,得到最优分类目标函数:
2.2 非线性支持向量机
对于输入空间中非线性分类问题,可以通过非线性变换将它转化为某个维特征空间中的线性分类问题[5],在高维特征空间中学习线性支持向量机。由于在线性支持向量机学习的对偶问题里,目标函数和分类决策函数都只涉及实例和实例之间的内积,所以不需要显式地指定非线性变换,而是用核函数替换当中的内积。
L(x,z)为一个核函数,是一个从输入空间到特征空间的映射φ(x),对于任意输入空间中的x与z,都存在L(x,z)=φ(x)φ(z)。对于线性支持向量机中的对偶问题,也都可以用核函数L(x,z)代替内积,所求解得到的非线性支持向量机为:

至此,可将非线性支持向量机学习算法的运算推导过程归纳如下:
输入:数据训练集T={(x1,y1),(x2,y2),...,(xN,yN)},其中xi∈Rn,yi∈[-1,垣1],i=1,2,...,N
输出:分离超平面和分类决策函数
选取适当核函数K(x,z)和惩罚参数C>0,构造求解二次规划问题
引入核函数及Lagrange 优化方法,得最优目标函数求解式:
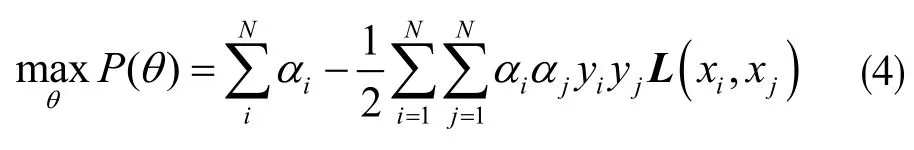
式中,L(xi,xj)=φT(xi)φT(xj),满足αiyi=0;0≤αi≤C,i=1,2,...,N。φT(xi)是样本数据从非线性函数映射投影到高维度空间后的特征向量。L(xi,xj)是xi和xj在高维空间下的内积。
最终得到的分类决策函数表达式为:

2.3 核函数
对于不同样本数据,由于算法不同,需使用不同核函数,所生成分类模型也不同[6],具体如下:
线性核函数:
通过对样本数据原始空间的处理,筛选出相应分类超平面:

多项式核函数:
通过内积运算出一个d阶多项式,规律为:d越大,运算越复杂,核函数推广能力就不断退化:

Sigmoid 核函数:

高斯径向基核函数:

其中,σ为径向基半径。高斯径向基主要应用于局部性核函数。
3 新算法建模与流程
新算法将缺陷图像样本集数据每个分类训练出对应的分类模型。在训练过程中,使用高斯径向基核函数作为分类核函数,基于“一对一”方法进行分类识别,通过交叉投票验证预测结果,并最终确定分类模型结果。首先,对特征向量统一化提取并处理,挑选合适核函数,选定最优参数;其次,通过统一化处理样本数据集得到分类模型;最后,对钢材表面成像与缺陷图像进行分类,识别具体缺陷。
新算法的具体执行流程为:
步骤一:统一化特征值
在对图像中不同特征值的提取过程中,由于所提取特征值波动较大,为避免差值过大导致筛选特征值太复杂,在将特征值进行训练之前,需要对输入值进行统一化处理,在缺陷特征值向量作用下,保证其值分布在[-1,1]范围之内,并满足特征值提取的三个基本标准:特殊性、简易性、低维性[7]。
步骤二:挑选核函数
在训练数据过程中,并不是全部类型数据都线性可分。在对非线性可分的数据的处理中,需要引入核函数来处理。核函数作用是将线性不可分数据通过维度转换,使得数据集处在线性下可分[8]。在众多类型的核函数中,高斯径向基核函数在局部范围内性能最强,收敛域相对较宽;其学习能力随着参数σ自身减小而增强。新算法就选定该核函数。
步骤三:确定并挑选最优值
任意的取值会导致SVM 分类模型欠优。由于分类器正确分类的正确率与训练参数不存在关联性,在实际训练过程中,可以根据实际情况去选取最优参数值,以保证预测未知数据时的正确性。
步骤四:训练分类模型
数据样本集存在多种类别数据,在进行多分类情况下,SVM 二分类模型需要选取“一对一”训练方法。针对不同训练类别,所训练出来模型的子模型的数量为CN2=N(N-1)/2。
步骤五:进行分类
采用“一对一”训练方法进行多分类训练,将不同训练样本模型结构放入不同训练子模型中预测,通过交叉验证方式验证投票,最终确定识别结果。
4 基于支持向量机的缺陷检测算法
在数据样本集中存在N个数值,将其中任意两个样本点建立关联。对于N个样本点,选取N-1 条边,构造样本数据集中的实际分布连续拟合评估模型。作为样本数据集的流形分布的简化分类模型,称为最小生成树分类模型。
构建虚拟目标样本点yi,满足:

式中,0≤λij≤1。
最小生成树分类模型构建过程为:在已确定N个样本点中选取N-1 条边,要求所选取边不能形成闭环连通,且所选取边的权值和最小,允许存在多种权值最小但所选取边不同的情况。
样本点yi与目标集V所形成最小生成树最短路径为:

由几何学原理可知,样本点yi在边uij上映射投影为:
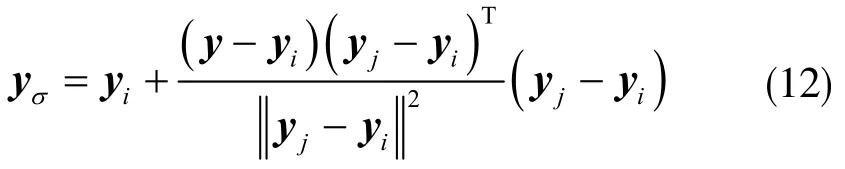
在相对位置的情况下,d(y|uij)形式是不同的。有两种情况:①yi映射投影在边uij上;②yi映射投影不在边uij上。综合考虑d(y|uij)中y 到yi、yj、yσ最小距离为:
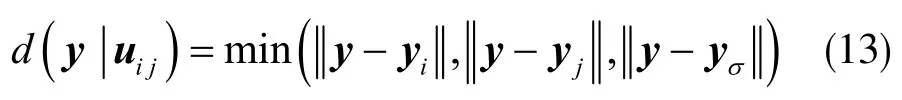
判断d(y|uij)≤R,若成立,则y 是目标分类,否则不是。
考虑样本数据集分布情况不同,存在稀疏及稠密两类,优化动态调整生成树的覆盖半径。半径对于分类精度影响很大,容易导致分类、识别出错。
自适应半径优化调整满足:
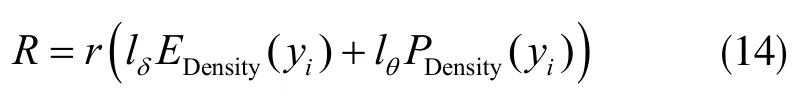
其中0≤lθ垣lδ≤3。
lθ和lδ依据样本集动态调整阈值,选择满足分布特点最优值。通过对lθ和lδ调整让边密度EDensity(yi)和点密度PDensity(yi)跟半径实现自适应。
样本点yi在最小生成树必存在投影点Vi:

新算法依据R和d(y|uij)数值间关系去判断目标分类。
将最小生成树分类模型识别目标分类作为SVM 算法的模型输入。至此,完成整个SVM 缺陷检测分类算法。算法整体训练流程见图2。

图2 模型训练流程
5 算法测试
算法测试选取两组钢材样本A、B,样本数量分别为300、400 个。两组样本数据中存在有表面破损、小裂痕、氧化、酸化、电镀痕等等缺陷类别,A 组中选取样本1、4 为目标分类,2、3、5 为非目标分类。B 组中选取样本2、3、4 为目标分类,1、5 为非目标分类。
测试采取钢板表面图像,照明方式为暗场,相机垂直于钢板。通过反复调整摄像参数,得到正常、小裂痕、边角裂痕、小斑点等钢板表面图像。两组样本的典型样本数据集如图3 所示。

图3 部分样本数据集
基于所采取图像数据样本集,确定所需分类新类别,采用交叉验证法验证新算法和传统SVM 缺陷识别率,对比结果见表1。

表1 钢材表面缺陷识别率对比
根据表1 可知,新算法在识别新类别基础上,阻止了SVM 新类别对分类模型的影响,对现存缺陷类别达到了较理想的效果,满足目前工业界的分类精度需求。
6 结 束 语
所提出的新的视觉检测算法基于支持向量机,将之应用于钢材缺陷分类检测中加以验证。新算法利用高斯径向基核函数和“一对一”分类方法,也使用了最小生成树判别分类算法,建立了自适应优化半径算法,确定了最优目标函数,保证了SVM 算法在多分类上精度更准确,能够满足当前工业制造业对缺陷检测的要求。

