扭摆式MEMS电容加速度计动态性能分析
齐志华,张志勇
(中国电子科技集团公司第十三研究所,石家庄 050051)
1 引言
MEMS(Micro-Electro-Mechanical Systems)传感器具有体积小、集成度高、成本低、性能优异、稳定性好、可靠性高等优点,被广泛应用于航空航天、汽车导航、消费电子、工业控制等诸多领域[1]。常见的MEMS 传感器包括加速度计、麦克风、压力传感器、陀螺仪、微马达等类型,其中MEMS 加速度计是最典型和成功的应用之一。MEMS 加速度计根据不同的工作原理可以分为电容式、压阻式、压电式、谐振式和伺服式等类型,其中MEMS 电容式加速度计的结构原理简单,加工工艺与IC 集成电路加工工艺兼容,集成度高,易于实现批量生产,成为应用最广泛的加速度计传感器之一。
系统的动态性能是衡量加速度计性能的重要指标,而系统阻尼是影响动态性能的主要参数,如何准确分析加速度计的阻尼特性和动态性能,成为加速度计设计的难点。Langlois、Bao、Pan 和Li 等[2-7]对扭摆式微平板谐振器的阻尼特性进行了分析,研究成果显著。本研究是在已有研究的基础上,针对扭摆式MEMS 电容加速度计,对其系统的阻尼特性和动态性能进行进一步研究和分析。
2 工作原理
扭摆式MEMS 电容加速度计主要由MEMS 敏感结构和ASIC 电路组成。当系统接收到加速度输入时,受惯性力矩的作用,敏感结构将产生一定的转动位移。转动位移的变化被转换为电容的变化量。ASIC 电路通过检测和处理电容变化信号,最终得到能表征加速度信号大小的输出信号,实现加速度信号的检测。扭摆式MEMS 电容加速度计可以等效为转动惯量-扭簧-阻尼系统,如图1 所示。其中:J表示转动惯量,C表示粘性阻尼系数,k表示扭转弹簧刚度,θ表示转角。
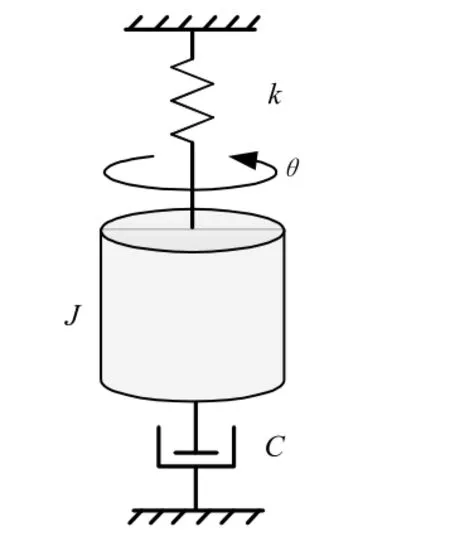
图1 扭摆式MEMS 电容加速度计原理图
根据牛顿第二定律可知,在加速度载荷的作用下,由于惯性力矩的作用,敏感结构将绕定轴转动,转角θ(t)满足动力学方程[8]:
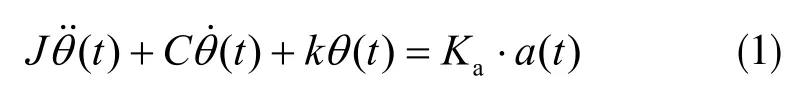
式中,Ka表示扭转系数,a(t)表示输入加速度,对上式进行Laplace 变化,可得到a(t)与θ(t)的传递函数:

式中,s为拉氏变换的复变量,设该加速度计的无阻尼固有频率为,阻尼比为,系统的传递函数可以转化为:

从式(3)可见,系统的动态特性与阻尼比ξ、无阻尼固有频率ωn、转动惯量J和扭转系数Ka有关;而阻尼比ξ由阻尼系数C、结构刚度k和转动惯量J决定;无阻尼固有频率ωn由结构刚度k和转动惯量J决定,由此可知,要分析扭摆式MEMS 电容加速度计的动态性能,需要知道C、k、J和Ka四个系统参数。
3 理论分析
扭摆式MEMS 电容加速度计的结构简图如图2所示,它主要由检测质量,弹性梁、固定端和检测电极组成。检测质量通过弹性梁连接到固定端,固定端固定于基板上,实现整个检测结构的悬挂。

图2 扭摆式MEMS 电容加速度计结构简图
图中,Lx和Ly分别表示检测质量的长度和宽度;l表示转轴到检测结构中心的距离;Tp表示结构厚度,g0表示检测质量与基板的间隙(即薄膜气体厚度)。当敏感方向有加速度输入时,在惯性力矩的作用下,检测质量会绕定轴转动,在基板上的检测电极与敏感质量之间形成差分电容,ASIC 电路通过检测和处理差分电容信号最终得到输入的加速度信号。
扭摆式MEMS 电容加速度计的弹性梁可以简化为如图3 所示的形式。弹性梁的一端连接到固定端,另一端连接到检测质量。设弹性梁的长度为L,宽度为ww,高度为h,当检测质量发生扭转运动时,弹性梁将发生扭转,转角为θ。
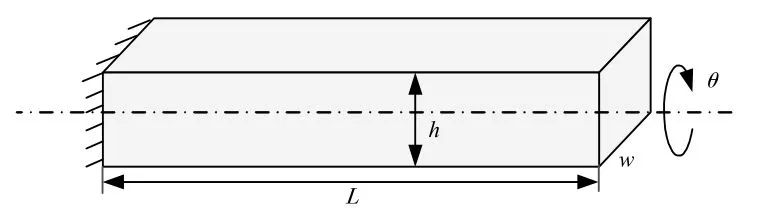
图3 扭转弹性梁简化模型结构图
根据材料力学原理,弹性梁提供的扭转刚度为:

式中,G表示材料的剪切弹性模量。可见,扭转刚度k与弹性梁宽度ww的三次方成正比,因此很容易通过调整弹性梁的宽度来获得期望的扭转刚度值。
根据动力学原理,质点的转动惯量表示为:

式中,mo表示质点质量;r表示质点到转轴的垂直距离。从图2(a)可见,若将检测质量看作是无数个质点的集合,则检测质量的转动惯量可以表示为:
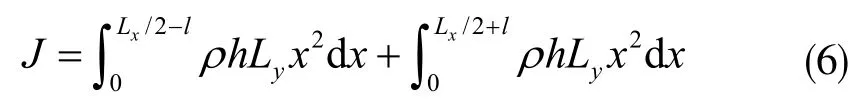
式中,ρ表示材料的密度,式(6)可以进一步简化为:

从式(7)可见,检测质量的转动惯量仅和其特征尺寸、材料属性和转轴位置有关,与结构刚度和转动角度无关。
扭转系数Ka表征了系统的摆动属性,公式为:

式中,m表示结构的总质量,rc表示检测质量的质心到转轴的垂直距离,rc=l。
系统阻尼是决定加速度计动态性能的重要参数,阻尼效应的强弱会影响器件的工作带宽、带内平坦度、品质因数及机械噪声等性能参数。扭摆式MEMS 电容加速度计的阻尼主要来源于材料内部的结构阻尼和气体粘性阻尼。通常情况下结构阻尼比气体粘性阻尼低几个数量级,可忽略不计。气体粘性阻尼分为滑膜阻尼(Side Film Damping)和压膜阻尼(Squeeze Film Damping),各自对应的平板运动情况如图4 所示。

图4 平板运动示意图
由于敏感结构和基板间存在薄膜气体,当敏感结构平行于基板运动时,敏感结构将带动间隙中的气体运动,气体对敏感结构的反作用力即为滑膜阻尼;当敏感结构垂直于基板运动时,间隙中的气体受到挤压发生水平运动,气体对挤压产生的反作用力即为压膜阻尼。对于扭摆式MEMS 电容加速度计,当有加速度输入时,其工作形式为绕定轴的扭转运动,系统的压膜阻尼远大于滑膜阻尼,由此,在此处仅需考虑压膜阻尼对系统动态性能的影响。
根据Bao 等人的研究,间隙气体的控制方程可以用Reynolds 方程表示:

式中,p(x,y,t)=pa垣Δp,表示结构与基板间的气体薄膜压强,pa表示气体压强,Δp表示压强的变化量;μ表示气体的运动黏度;h(t)=g0垣xθejwt,表示间隙中气体薄膜厚度;θ表示结构扭转角度。对控制方程进行线性处理后,利用双正弦三角级数近似表达气体薄膜的压力分布函数p(x,y,t),可以得到挤压模气体对矩形板的总力矩[6]:
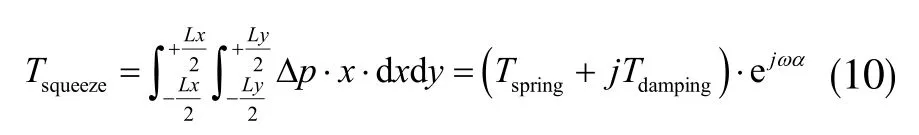
式中,α2=,μeff表示气体的等效粘度系数。总力矩的实部Tspring=,表示气体对结构的刚度力矩;总力矩的虚部Tdamping=,表示气体对结构的阻尼力矩。具体表达式分别为:
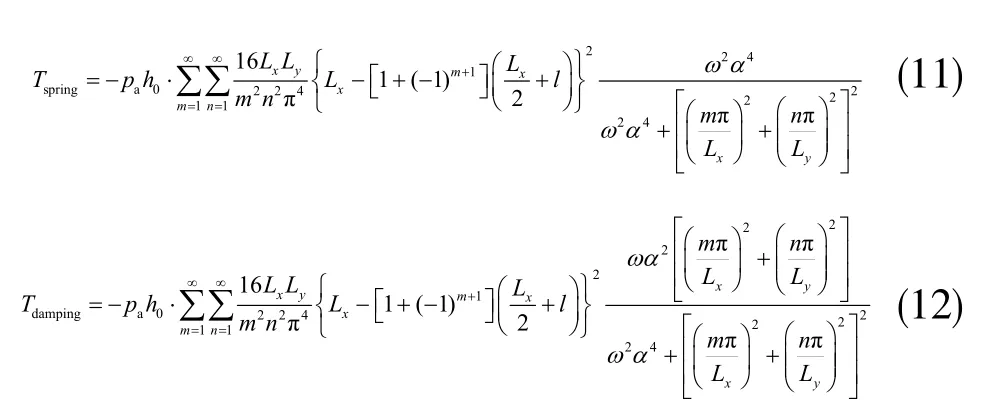
式中,m=1,2,3…;n=1,3,5…。由于刚度系数和刚度力矩,阻尼系数和阻尼力矩存在如下关系:

至此,即可以得到刚度系数Kθ和阻尼系数Cθ的表达式:

其中,σ=ωαLx2。
4 动态性能
给定一组扭摆式MEMS 电容加速度计的结构参数如表1 所示。
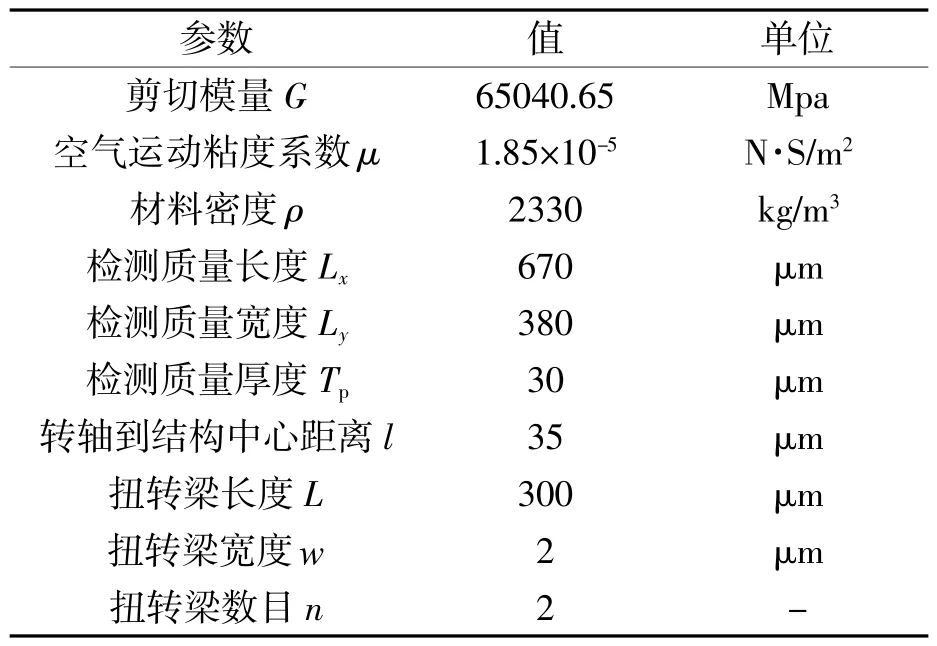
表1 扭摆式MEMS 电容加速度计结构参数
根据式(4)、(7)、(8),可以计算得到结构刚度k=33228 μN/μm,转动惯量J=0.00328 kg·μm2,扭转系数Ka=6.2288×10-7kg·μm。
从式(15)、(16)可以看出,当结构的尺寸参数和材料属性一定时,薄膜气体的刚度系数Kθ和阻尼系数Cθ主要由气体压强Pa和薄膜气体厚度g0共同决定。加速度计若采用常压封装,即气体压强为标准大气压(101325Pa),则刚度系数和阻尼系数随扭转振动频率的变化关系如图5 和图6 所示。
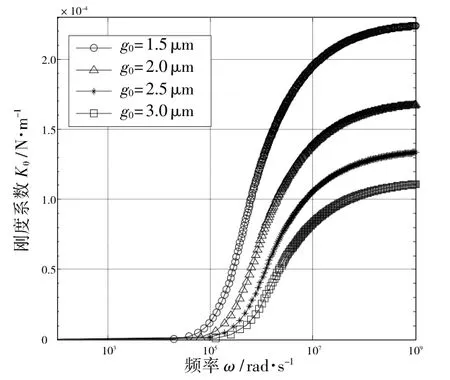
图5 刚度系数Kθ 与振动频率ω 关系曲线
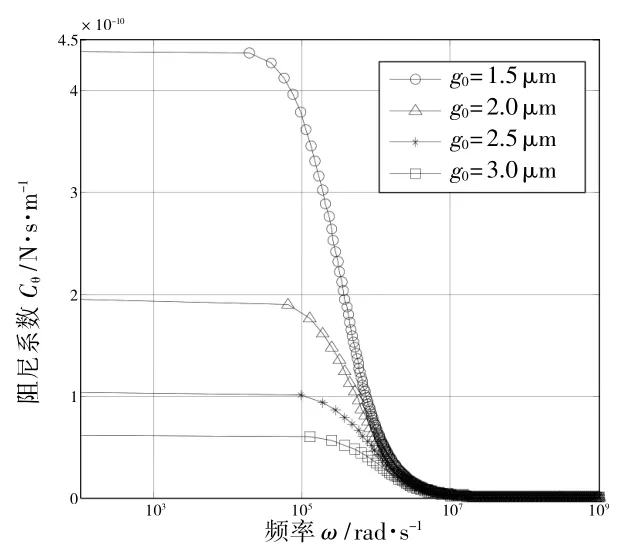
图6 阻尼系数Cθ 与振动频率ω 关系曲线
从图5 和图6 可以看出,随着扭转振动频率的增大,薄膜气体的刚度系数增大,阻尼系数减小,当振动频率在104~106rad/s 范围时,刚度系数急剧增大,阻尼系数急剧减小。因此,在低频条件下气体对结构的反作用力主要表现为阻尼效应,在高频条件下则主要表现为刚度效应。由于开环扭摆式加速度计通常工作在低频区,因此气体的阻尼效应成为影响系统动态性能的主要因素。
当气体压强为标准大气压时,扭摆式加速度计的频率响应如图7 所示。从图中可以看出,当气体压强为标准大气压时,扭摆式MEMS 电容加速度计由于挤压模阻尼过大,使得传感器的二阶系统处于过阻尼状态,系统的带宽(-3 dB)最大约为128 Hz,很明显这是不希望看到的。因此,在加速度计设计时常采用真空封装或者加工阻尼孔的方式来调整系统的动态特性。
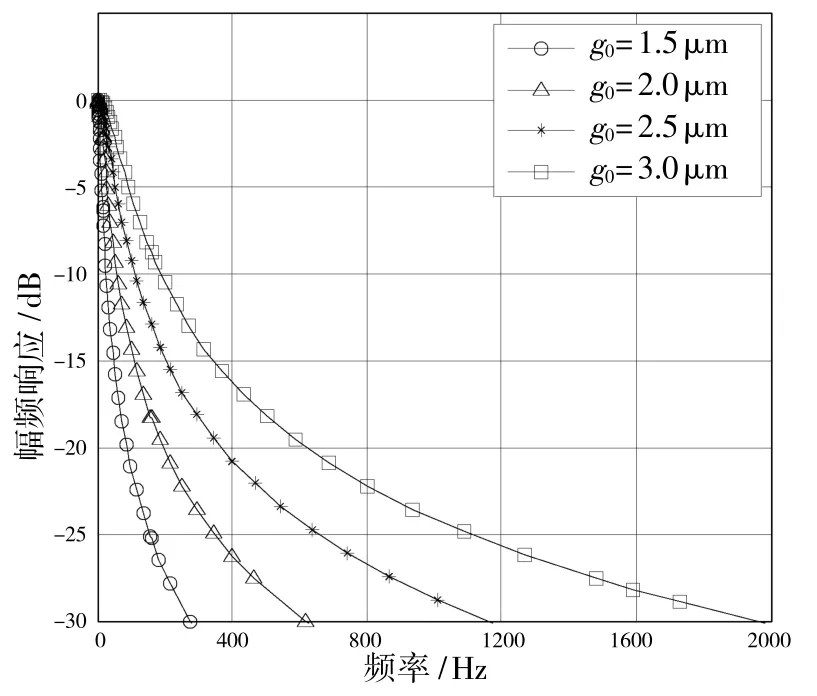
图7 标准大气压下系统频率响应曲线
若采用真空封装或加工阻尼孔后等效气体压强为100Pa,则可得到传感器的幅频特性如图8 所示。

图8 气体压强为100 Pa 时系统频响曲线
可以看出,通过改变气体压强Pa和薄膜气体厚度g0,容易调节系统的动态特性。根据自动控制理论可知,当系统阻尼比为ξ=时,系统有最佳的动态性能。若气体压强为100Pa,通过计算可以得到系统动态性能最佳时,结构与基板的间隙为1.15μm(薄膜气体厚度),此时系统的幅频特性曲线和单位阶跃响应曲线如图9 所示。此时系统的带宽(-3dB)为1598Hz。
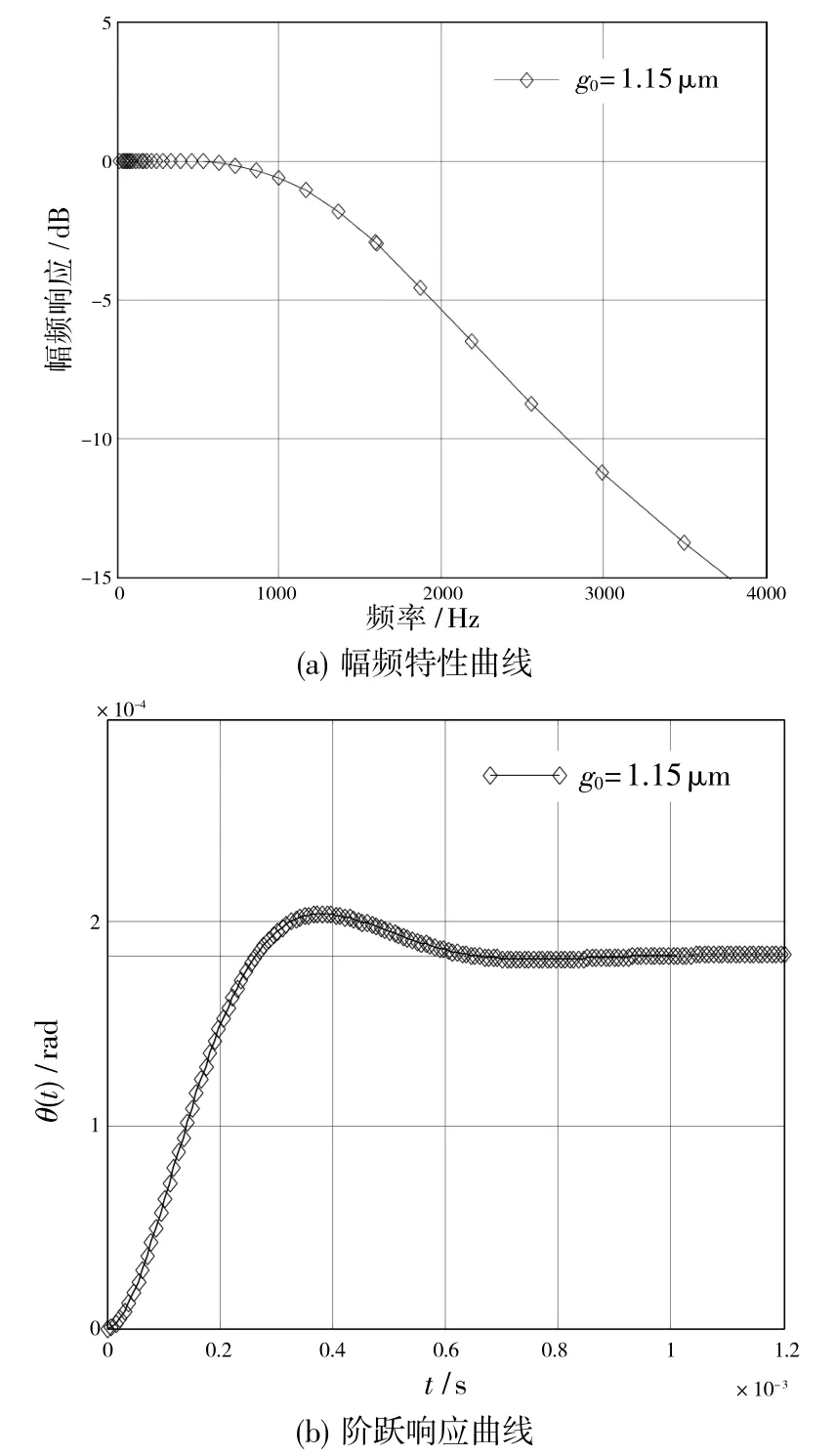
图9 气体压强为100Pa 时系统幅频特性与阶跃响应
至此,基于上述分析结论,即可对扭摆式MEMS电容加速度计的动态性能进行优化设计,进而合理设计系统的结构形式和尺寸参数,最终得到综合性能较好的加速度计。
5 结 束 语
通过对扭摆式MEMS 电容加速度计建立特征模型,对其工作原理和动态性能进行研究分析,推导出了特征模型的系统传递函数,给出了系统模型的结构刚度、转动惯量、扭转系数和阻尼系数的解析公式。在理论计算基础上仿真了系统阻尼特性的影响因素,确定了气体压强和气体薄膜厚度是最重要的影响因素。通过一组给定的结构参数,深入研究了系统阻尼特性对动态性能的影响。研究结论对于扭摆式MEMS 电容加速度计的动态性能设计具有非常重要的参考意义。

