偏差补偿稀疏自适应滤波算法

李立立，郭 莹

（沈阳工业大学信息科学与工程学院，沈阳 110870）

1 引言

在例如回声信道[1-2]等许多实际环境中，信道具有一定的稀疏性，即信道中大部分系数都为零。受到压缩感知等稀疏理论的启发[3-7]，研究者们基于范数约束，提出自适应滤波算法——零吸引最小均方算法[8]（Zero Attraction Least Mean Square algorithm,ZA-LMS），在标准的LMS 算法的代价函数中加入权系数的l1范数，对权系数施加向零吸引的力，在迭代时修正权系数，因此加快了算法的收敛速度。虽然ZA-LMS 算法具有良好的性能，但是未考虑到输入信号受噪声干扰的情况，从而导致ZA-LMS 算法在迭代时会出现估计结果的偏差。为解决这一问题，一些相关算法被提出，如：偏差补偿归一化LMS（Bias-compensated normalised LMS algorithm,BCNLMS）[9]，偏置补偿零吸引NLMS（Bias-compensated zero attracting normalized LMS algorithm,BC-ZANLMS）[10]等。基于已有的研究，在此将ZA-LMS 算法与无偏估计相结合，提出偏差补偿稀疏自适应滤波算法，以求实现更低的稳态误差、更快的收敛速度和更好的跟踪性。

2 相关算法

2.1 LMS 算法

所提出的自适应滤波器基本结构框图如图1 所示。图中，n为算法的迭代次数；L为滤波器阶数；x(n)是输入信号；d(n)是期望信号；e(n)表示期望信号与滤波器的输出信号之间的误差；z(n)是均值为0、方差为σz2且独立于任何信号的加性高斯白噪声；η(n)是输入信号中存在的噪声。

图1 自适应滤波器结构

输出信号y(n)表示为：

其中，x(n)=［x(n),x(n-1),...,x(n-L垣1)］T为输入信号向量，w (n)=［ww(n),ww(n-1),...,ww(n-L垣1)］T为权系数向量，上标T是转置符号。

期望信号d(n)为：

其中w*为最优权系数。

在第n时刻，期望信号d(n)和输出信号y(n)之间的输出误差e(n)为：

LMS 算法的更新方程则为：

其中，μ是控制收敛速度和稳态的步长。

2.2 ZA-LMS 算法

ZA-LMS 算法是在LMS 算法代价函数的基础上，为了改善标准LMS 算法的性能，增加了权系数的l1范数：

其中，λ是正常量，用于控制范数的平衡因子。

利用梯度下降法，ZA-LMS 算法的更新方程为：

其中，ρ=μλ，sgn[.]是符号函数，定义为：

上述ZA-LMS 算法是基于l1范数约束的自适应滤波算法，在稀疏系统中可以加快算法的收敛速度，但是当输入信号受到噪声干扰时精度会下降。为了解决这个问题，在此提出一种偏差补偿稀疏自适应滤波算法。

3 偏差补偿稀疏自适应滤波算法

3.1 无偏准则

在某些实际应用中，输入信号x(n)被噪声η(n)破坏。按照图1 的结构，重新定义输入信号为：

其中，η(n)=［η(n),η(n-1),...,η(n-L垣1)］T为输入噪声，其均值为0 且方差为ση2。

因此，重新定义误差函数：

定义权系数误差向量w～(n)为滤波器权系数w(n)和w*之间的差：

理想的情况是在稳态下权系数误差向量w～(n)接近零，即w(n)趋近于w*。因此，当算法处于稳定状态时，应满足下式：

式(11)被称为无偏准则，在稳态情况下是有意义的。

3.2 CZA-LMS 算法

当输入信号受到噪声干扰时，使用式(4)进行参数估计会给算法带来偏差，因此，为了减小输入噪声产生的影响，在式(4)中添加偏置补偿矢量C(n)：

由于C(n)只与输入噪声有关，因此对该补偿项进行推导时去掉sgn 项。将式(12)两侧减w*，并求期望，其递推方程可表示为：

使用无偏准则推导偏置补偿向量C(n)，将式(11)代入式(13)，得到偏置补偿矢量C(n)的条件如下：

计算式(14)左侧，并假设z(n)，η(n)，x(n)均与w(n)统计独立：

将式(15)代入式(14)，可以得到偏差补偿矢量：

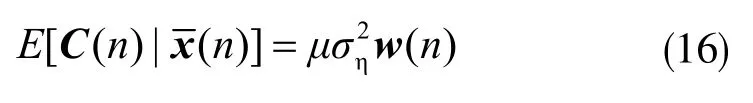
因此，新算法的更新方程为：

4 仿真实验

为进一步证明算法的有效性，在不同的条件下，对LMS、ZA-LMS 和CZA-LMS 算法进行仿真实验。实验分两部分进行：实验1 是在输入信号受到噪声干扰的情况下，对各个算法的收敛性能做出比较；实验2 是在实验1 的基础上增加了未知系统的时变的环境，以此来模拟更为接近真实的环境，验证各个算法的跟踪性能。

4.1 性能指标及参数设置

实验中未知系统共有32 个系数，输入信号采用均值为0 的高斯白噪声，设置信噪比为30dB。

为保证实验的公平性，每个实验仿真结果都采用30 次独立实验的平均结果。每个实验中各对比算法采用等效步长，为对比各方法的性能表现，可对实验结果采用归一化均方偏差（Normalized Mean Square Deviation,NMSD）的收敛曲线作为衡量和分析性能的指标，其定义为：

其中w(n)为滤波器权系数，w*为未知系统的最优值，归一化均方偏差值越小，说明自适应滤波器越接近待估计系统。

为便于计算，由表1 给出算法的参数设置。

表1 实验参数设置

4.2 算法收敛性测试

采用稀疏度为0.8619 的稀疏环境，输入信号处的干扰噪声为30dB 的高斯白噪声，按照表1 中的参数进行测试，对比结果如图2 所示。由图中可以看出，在输入信号受到噪声污染的情况下，CZALMS 算法的收敛速度快，稳态误差低，算法性能优于LMS 算法和ZA-LMS 算法。

图2 稀疏系统下算法性能比较

4.3 算法跟踪性测试

在时变系统的情况下，未知系统每经过5000 次采样间隔跟踪非零系数位置和取值的变化。第1 时间段是稀疏度为0.8619 的稀疏系统；第2 时间段是稀疏度为0 的非稀疏系统。测试算法及相应的参数设置同前实验，独立运行30 次后各个算法的收敛曲线如图3 所示。

图3 时变稀疏系统下算法性能比较

由图可知，与LMS 算法和ZA-LMS 算法相比，CZA-LMS 算法的跟踪性更好且稳态误差较低。当未知系统的稀疏度发生变化时，CZA-LMS 算法快速地跟上了系统的变化，表明ZA-LMS 算法的跟踪性能良好。

5 结 束 语

基于对稀疏自适应相关算法的讨论，提出了偏差补偿稀疏自适应滤波算法，可以有效地解决在输入信号受到噪声干扰以及在时变系统情况下的稀疏系统辨识的问题，并进行了相应的实验仿真。与传统算法相对比，新算法的性能在输入信号受到噪声干扰和时变系统两方面通过验证。新算法对系统辨识的进一步研究具有重要意义和实用价值。