基于最小二乘法的三轴气浮台质心位置测算方法

宋院归，胡奇飞

（中联恒通机械有限公司，长沙 410073）

1 引言

三轴气浮台通过气浮球轴承实现近似无摩擦的系统来模拟太空失重环境，需要通过调平衡装置将质心调节到转动中心的位置，消除重力带来的干扰力矩。因此，调平衡技术是实现高精度气浮台的关键技术。一般而言，自动调平衡技术可实现比人工调平技术更高的效率和精度，是当前研究的热点。为实现精确调平衡，必须先测算出质心的精确位置。通过CAD 软件建立气浮台的三维模型，可以初步计算气浮台的质心位置，但由于电线、焊接点等零部件建模存在困难，这一方法无法精确计算出质心的位置。起初，研究人员通过测量气浮台的摆动周期来测算质心位置的偏移，进而进行配平。这种方法将气浮台等效为3D 复摆[1-2]，但这一方法需要反复测量气浮台的摆动周期，所需调节时间较长。随后，人们提出基于气浮台的刚体动力学方程来控制执行机构，调节质心位置，文献[3-4]给出通过2 个倾角传感器实现水平方向自动配平的方法，文献[5-6] 提出在已知转动惯量的情况下计算质心的方法。基于已有研究成果，在此建立三轴气浮台的动力学模型，采用最小二乘法处理姿态信息、计算质心位置，求解配重滑块位置，实现气浮台自动调平衡，并与常规的周期反馈算法进行比较。

2 三轴气浮台动力学模型建立

三轴气浮台由支撑座、气浮球轴承和转动台体三部分组成。气浮球轴承通过球窝上布置的喷嘴喷出高压气体，在球窝与球头间形成一层极薄的气膜，实现三轴近似无摩擦转动。气浮台采用伞形结构[7-8]，其三维模型如图1 所示。

图1 气浮台三维模型

通过Pro/E 建立三维模型，计算得到气浮台的质量：m=136.95322kg，其质心位置偏移为：r=[0,0,-1.8519493×10-3]m，气浮台相对于转动中心（球头球心）的转动惯量为：I=[19.021405,17.275641,19.0 21405]kg·m2。

由于台体变形较小，假设台体为刚体，按照欧拉角旋转公式，依照Z-Y-X顺序旋转，可确定由惯性系到随体系的变换矩阵Cib如下式：

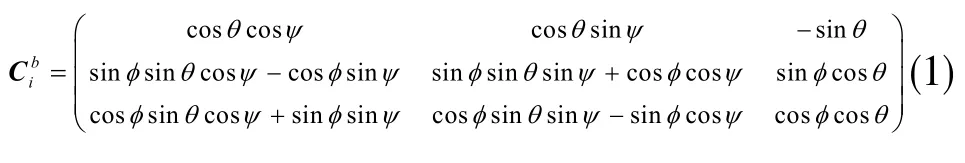
其中，Ψ为偏航角；θ为俯仰角；φ为滚转角。对于欧拉角速度方程，有：

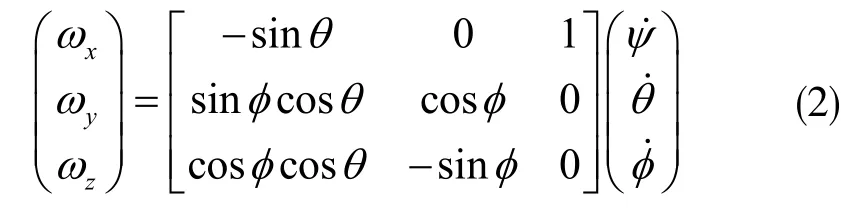
又有动量矩定理：

其中，M0为作用于平台的外力矩矢量和。由于旋转中心与质心不重合，所以又有：

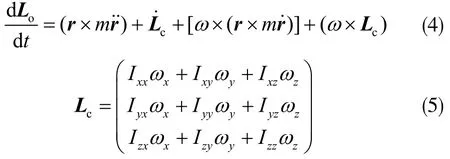
其中，LC为平台相对于质心的角动量，ω为平台相对于惯性系的角速度（单位为°/s）。

将式(4)和式(5)代入式(3),并写成Aω˙垣B=M 的形式，其中，M 为和外力矩，这里不考虑重力以外的其他干扰力矩，同时台体转速较慢，ω、r 均为小量，I只考虑主惯量，故得：

3 基于复摆模型的质心位置测算

当气浮台小角度摆动时，可以将台体近似作为复摆处理。将气浮台的运动分解，假设只绕X轴运动，则由复摆周期公式：

由此可求解得到质心在竖直方向的偏移为：rz=，X轴水平方向质心偏移为：rxX≈rXsinα=，Y轴水平方向质心偏移为：ryX≈rXsinθ=，其中，α为X轴与x轴重合时的倾角，θ为台体转动180°后的倾角（Y轴）。按照这一方法计算，结果如表1 所示。

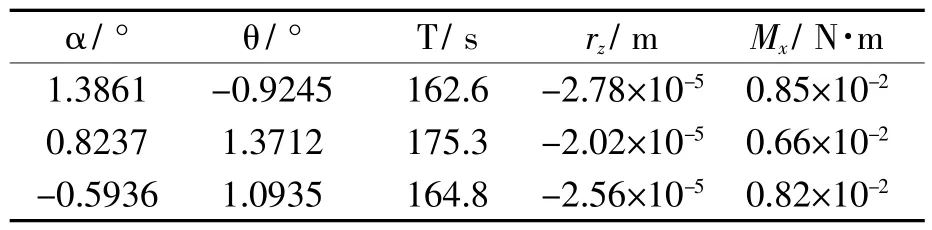
表1 基于复摆的质心测算结果

4 基于动力学反演的质心位置测算

4.1 基于最小二乘法测算质心位置

基于式(6)，可通过变形来求解质心位置，有：

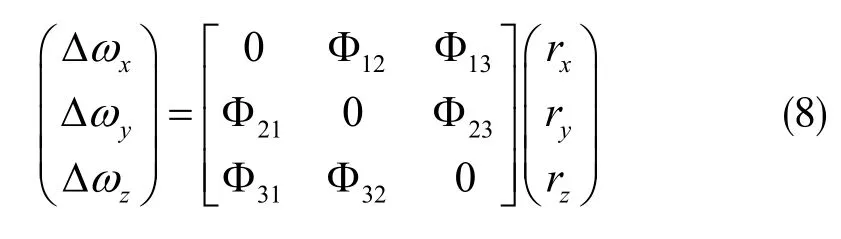
其中：

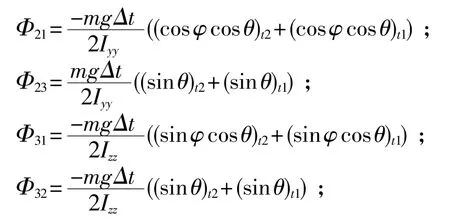
可将式(8)简写为：

对式(9)求广义逆矩阵，质心可通过最小二乘法求得为：

通过最小二乘法即可计算得到质心的位置。测算结果如图2 所示。

图2 质心测算结果

由图2 可知，基于最小二乘法质心算法收敛较快，可有效缩短测量时间，更快地实现质心调节；同时偏差较小，对质心位置的测量更加精确。

4.2 算法实现

基于最小二乘法的质心算法实现的总体流程可描述为图3 的流程图。

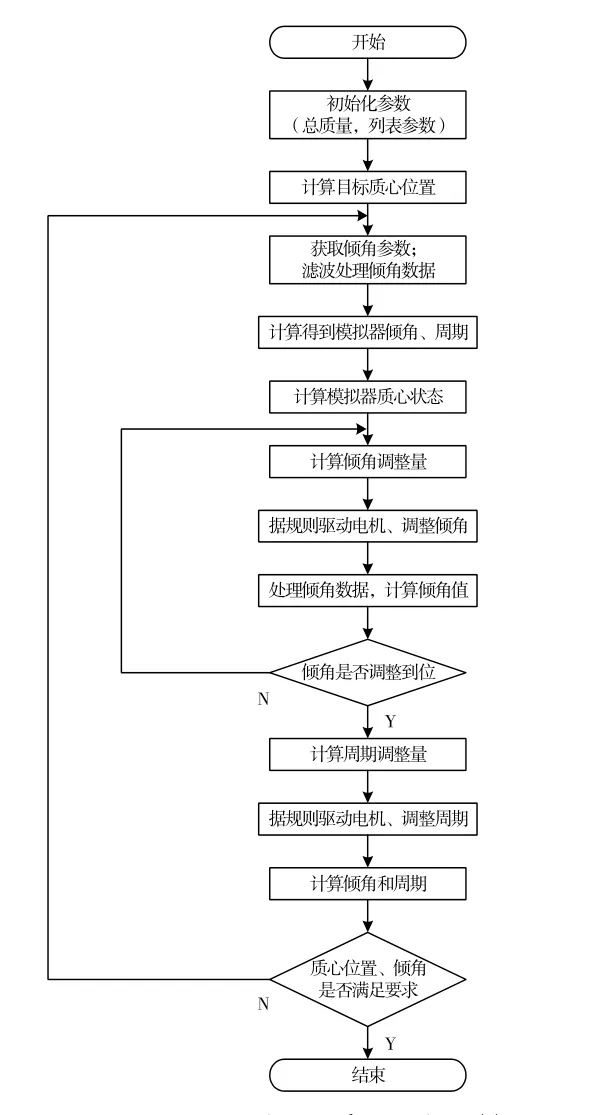
图3 基于最小二乘法质心算法流程

根据复摆公式(7)，三轴气浮台质心测量可根据气浮台的摆动周期来确定。由表1 可知，气浮台垂直方向质心与球心的偏移量小于10-5m 时，系统的干扰力矩为10-2N·m 量级，此时三轴气浮台摆动周期在160s 左右。

气浮台四个支腿上（相对支腿为一轴）各安装伺服电机，外加高精度丝杆与滑块，通过滑块移动调节台体的质心垂直方向和水平方向的偏移量。台体上布置一个两轴倾角仪，输出频率为100Hz，精度0.002°，测量台体角度信息，计算台体X轴或Y轴两个角度极大值的时间间隔，可得台体的摆动周期。实验中取X轴为计算依据。由于气浮台最大摆动角度仅为30 度，水平方向的过度偏摆可能导致气浮台触碰到防倾翻保护环，从而影响到整个系统质心发生变化，故此先做倾角调整再进行周期调整，并且设置衰减系数，防止调整过度。

倾角调整量可按如下两式相应地计算出来：

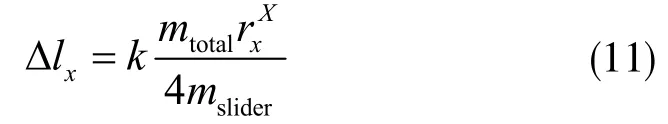
此时，当T＜100 s，k=0.8；当100 s＜T＜150 s，k=0.6；当T＞150s，k=0.4；

此时，当T＜100 s，k=0.8；当100 s＜T＜200 s，k=0.4；当T＞200s，k=0.3；

倾角的调整采用如表2 所示的方式进行调整。

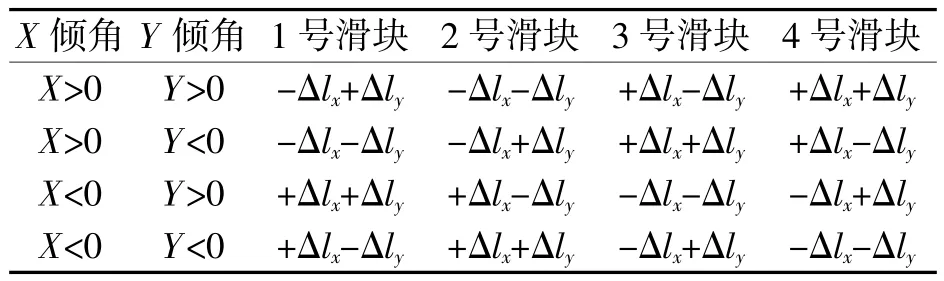
表2 倾角调整方式对应表

表中，采用X倾角大于0，则1、2 向下调整Δlx，3、4 向上调整Δlx，反之相反；采用Y倾角＞0，则2、3向下调整Δly，1、4 向上调整Δly，反之相反。

X轴和Y轴分开调整，一般可先调整X后调整Y。若不能向下调整，则只向上调整，进行迭代，直到倾角小于2°。

待倾角调整到2°以内，再调整周期。周期调整量可根据如下公式计算：

此时，当Tx＜100 s，k=0.8；当100s＜Tx＜150 s，k=0.6；当Tx＞150s，k=0.4。

根据上述式(11)～(13)进行迭代调整。其中周期调整采用4 个电机同时向上移动，若不能满足4 个移动，则采用2 个相对电机同向移动。

5 实验结果比较

在三轴气浮台上，以气浮台摆动周期大于160s为目标，此时系统的干扰力矩小于10-2N·m，分别采用周期反馈算法和基于最小二乘法的质心算法进行调试，比较各自的调试时间，比较结果见图4。

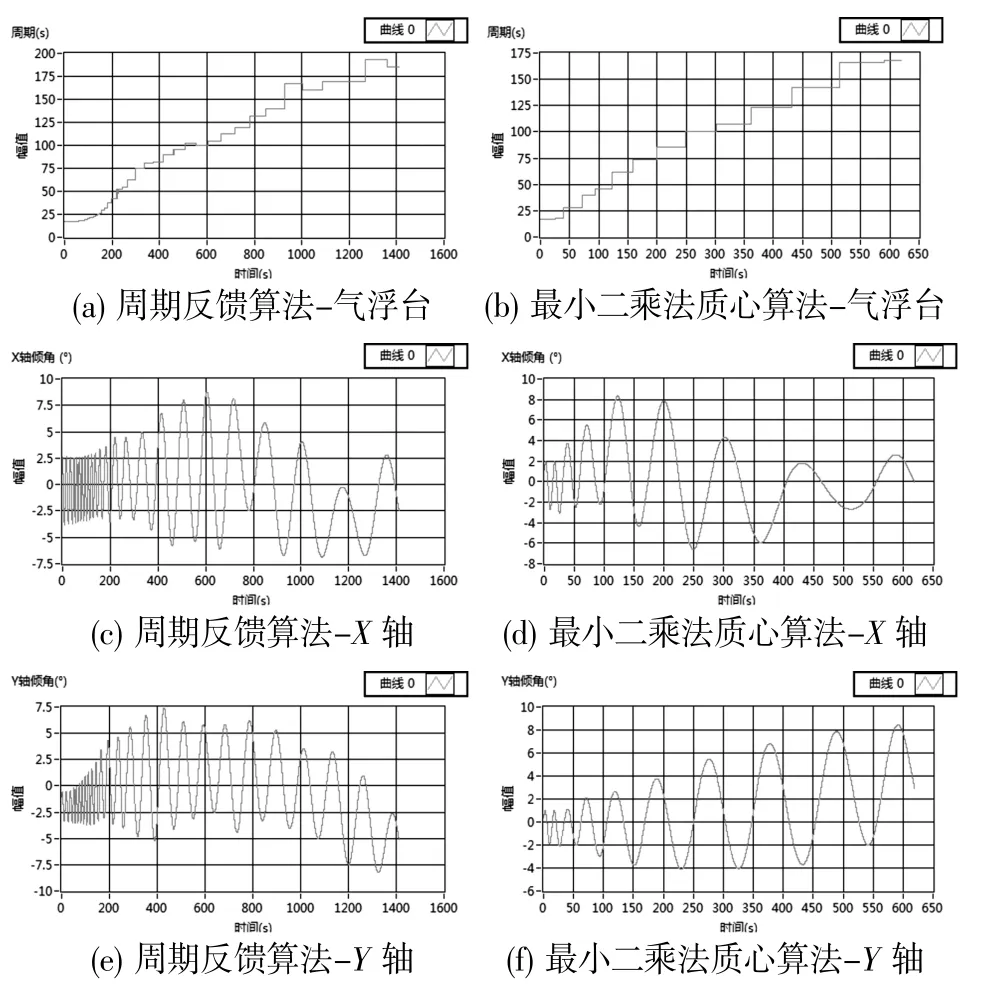
图4 两种方法的调试效果对比

从图4 可以看出，三轴气浮台使用周期反馈算法将摆动周期从22 秒调整到160 秒需要近16 分钟；基于最小二乘法质心算法只需要9 分钟左右，效率有较大提升。

6 结 束 语

在对三轴气浮台的动力学建模中，通过数值计算，仿真了其运动过程中的角度和角速度变化。通过仿真的角度变化数据，计算出气浮台的摆动周期，从而测算质心的位置。通过动力学反演的方法，采用最小二乘法处理姿态信息，并分析质心位置的计算速度与精度。通过实验对比，在三轴气浮台上分别采用周期反馈算法和基于最小二乘法质心算法进行调试，后者时间明显小于前者，有效提高了三轴气浮台的调试效率。