气泡微细化沸腾触发温度数值模拟研究

朱光昱，郭　勇，元一单，刘宇生，李 炜

气泡微细化沸腾触发温度数值模拟研究

朱光昱1,2，郭勇1，元一单1，刘宇生2，李 炜1

（1. 中国核电工程有限公司核电安全研究中心，北京 100840；2. 生态环境部核与辐射安全中心，北京 100082）

气泡微细化沸腾（MEB）现象具有极高的换热能力，成功工程化应用后将极大提升核电厂中高热负荷设备的安全裕量。本文参照以往研究获得的可视化研究结果，采用Fluent建立相关模型，综合考虑气膜附近Marangoni对流、蒸发冷凝作用以及温度对物性参数的影响，结合数值模拟手段和沸腾不稳定性分析对MEB现象的发生机理进行了研究。结果表明，在不同过冷度下，汽液界面处的蒸汽平均流速随着壁温升高而增大。蒸汽平均流速达到该过冷度下Helmholtz失稳极限速度时对应的壁温与在实验获得的MEB触发壁温十分接近，说明Helmholtz失稳可能是导致MEB现象中气膜发生破裂的原因。

气泡微细化沸腾；Marangoni对流；数值模拟；Helmholtz失稳

为了提高核电机组的经济性指标，大功率反应堆成为了现阶段三代堆型的主要发展方向，这使得严重事故后堆芯熔融物增多，提高了熔融物施加在压力容器内壁的热流密度，极大的降低了熔融物堆内滞留技术（In-vessel Retention，IVR）的安全裕量。近几十年发现的气泡微细化沸腾现象（Microbubble Emission Boiling，MEB），由于具有高于一般池沸腾临界热流密度（critical heat flux，CHF）的换热能力，被认为是提高堆内熔融物滞留安全裕量的理想手段。

自MEB现象被发现后，很多学者对气泡微细化沸腾的换热特性和沸腾现象进行了研究。Shoji等[1]以铂丝作为加热源成功观察到MEB现象。Tang等以及Suzuki等[2-4]分别以直径10 mm的铜作为加热源完成了一系列池式MEB实验。在他们的研究中发现，沸腾达到临界后，铜加热面上会形成一层气膜导致壁温飞升，当壁温达到一定温度时气膜迅速破裂从而使沸腾状态进度到MEB阶段。根据最近的实验研究[2]结果，随着液体过冷度的升高，触发MEB发生的壁温会逐渐降低。由于MEB现象十分剧烈，无法在实验中直接获取气膜或周围流场的信息，因此本文采用Fluent软件建立相应几何模型，结合数值模拟方法和沸腾不稳定性分析，对MEB现象的触发温度与Helmholtz失稳的关系进行了研究，探讨了MEB现象的发生机理。

1　几何模型

文献[4]中MEB实验台架的加热面为直径10 mm的圆形铜面。实验过程中，通过倾斜角度为18.5°的摄影仪拍摄沸腾现象，由此获得的刚进入MEB阶段时的沸腾现象如图1所示，加热面上的不稳定气膜在约1 ms的时间内处于与膜态沸腾状态类似的准稳态，随后迅速发生破裂。因此可以建立一个气膜模型，通过数值模拟手段分析准稳态阶段气膜内的流场，从而分析MEB的产生机理。

图1　气泡微细化沸腾现象

图2所示为根据沸腾现象建立的计算模型，在准稳态阶段的气膜可以简化为一个扁平的椭球体，椭球体长轴为11.2 mm，短轴为3.52 mm，底部与圆形加热面相接。与加热面结合后，椭球体剩余高度为2.55 mm。考虑到加热面和气膜的对称性，在数值模拟过程中只对几何模型的六分之一进行建模以减少计算量。

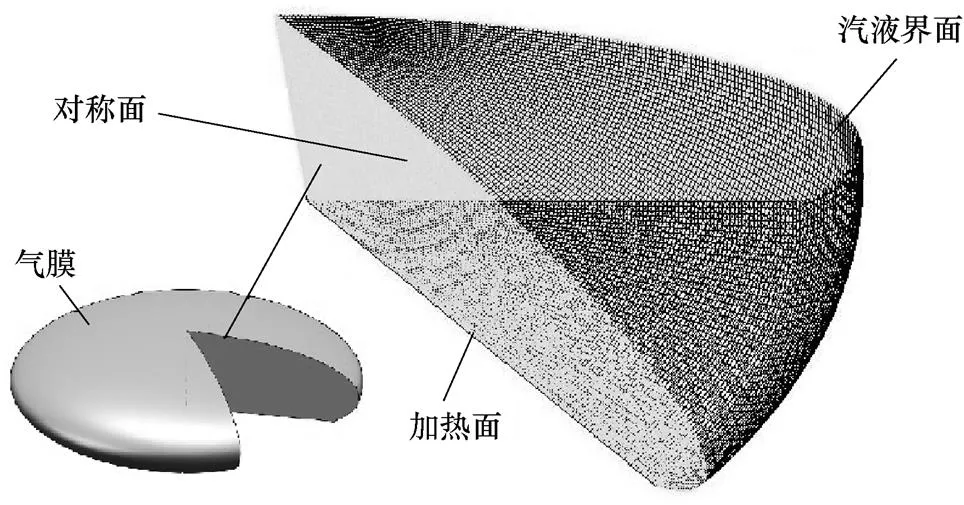
图2　计算域和网格划分

在预计算阶段，分别对比了水温343.15 K壁温438.15 K时，网格数为206 668、287 036、391 101的计算模型得到的蒸汽计算平均速度和最大速度，其结果如表1所示。其中，网格数为287 036、391 101模型得到的计算结果变化很小，因此最终采用的网格数为287 036。整体网格质量的Equi-size skew不超过0.51。

表1　网格敏感性分析

2　数学物理模型

2.1　计算模型和物性设置

参考以往蒸汽数值模拟研究[5-6]，湍流模型采用标准k-epsilon模型。由于最终采用网格宽度在0.04 mm左右，导致边界层处Y Plus值小于15，因此壁面函数采用Enhanced Wall Treatment。本文采用水作为工质进行计算，在计算过程中通过将工质的密度设置为不可压缩理想气体来模拟密度差导致的自然对流[7]。参考以往仿真经验[8]，模拟过程中考虑了温度对流体物性的影响，蒸汽的比热容、导热系数和粘度均设置为Fluent材料库自带的物性温度函数。

2.2　边界条件设置

计算域内，加热面和汽液界面均设置为壁面边界条件。加热面的为恒温壁面，汽液界面采用对流边界作为热力学边界条件，其中，传质换热系数采用公式（1）计算[9]：

fg——汽化潜热；

v——蒸汽密度；

v——蒸汽温度；

v——蒸汽压力；

参考以往MEB现象仿真经验，水作为工质时的换热系数可设置为230 000 W/m2·K[9]。

由于MEB现象仅在液体过冷度和壁面过热度足够高的工况下发生，目前普遍认为剧烈和蒸发冷凝作用，以及汽液界面附近存在由表面张力梯度引起的Marangoni对流是导致MEB发生时气膜破碎的原因[9]。图3为汽液界面附近的Marangoni对流的示意图，在温度差导致的表面张力梯度作用下，气相和液相分别受剪切力v和l作用，此时受力平衡可表示为：

式中：d/d——表面张力随温度的导数；

d/d——汽液界面上的温度梯度。

图3　汽液界面附近Marangoni对流示意图

根据池式MEB现象的可视化研究结果，气相的活跃程度远大于液相，可以认为准稳态阶段，表面张力梯度产生的Marangoni Stress完全作用于气相之上，则公式（2）可简化为：

据此，汽液界面处采用Marangoni Stress作为动量边界条件。水的Marangoni Stress边界条件应设置为-0.000 18 N/（m·K）[9]。数值模拟过程中，压力速度耦合采用SIMPLC算法，其中的畸变修正和压力方程亚松弛因子均设置为1，其余松弛因子保持默认值[7]。离散格式选项中，梯度采用Least Squares Cell Based，动量、湍流等其余项均采用二阶迎风格式。

3　模拟结果分析

图4展示了Tang等[2]以水作工质的实验中获得的MEB沸腾特性曲线。其中，CHF对应的壁面过热度和MEB触发温度分别随着过冷度升高呈现升高和降低的趋势，导致沸腾临界后的壁温飞升的幅度逐渐减小。由于MEB触发温度主要集中在壁面过热度45 K至60 K的区间内，在数值模拟过程中，以上述区间作为加热面温度的设置范围，分别计算不同过冷度和壁面过热度下的气膜速度场，从而分析MEB现象的产生机理。

图4　MEB沸腾特性曲线

图5所示为60 K过冷度下，壁温为（a）428.15 K和（b）438.15 K时，汽液界面和对称面上的速度场。在自然对流和Marangoni Stress的作用下，气膜内的蒸汽形成了一个循环流场，随着壁温提升汽液界面上的蒸汽流速也逐渐升高，但流场的形式没有发生变化。通过对比局部流场可以发现，汽液界面上的蒸汽流速明显高于其他区域，因此本文以汽液界面上的蒸汽平均速度作为循环流场的特征速度。

根据Helmholtz失稳条件[10]，沸腾过程中，导致蒸汽拥塞的气相极限速度与蒸汽脱离通道波长w的关系可采用式（4）计算。

一般情况下，w等于脱离加热面气泡的直径，在池式MEB沸腾现象中Marangoni对流速度场是轴对称的，因此采用等效半径作为气膜的特征尺寸。根据以往研究结果，较小加热面上的不同阶段的气泡可以近似按轴对称的回转体考虑。

对于几何形态类似图6所示的准稳态下的气膜，其等效半径可以按公式（5）来计算[11]：

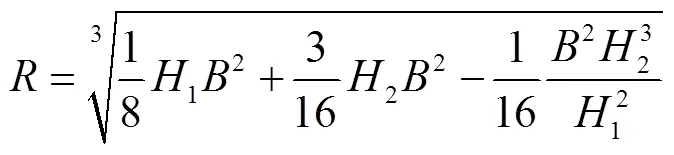
图6　气膜几何特征参数

图7示出了采用水作为计算工质时，数值模拟结果与图4中MEB触发温度的对比，其中共示出了：不同过冷度下采用公式（4）和公式（5）计算的Helmholtz失稳极限速度；不同过冷度和壁面过热度下通过数值模拟得到的汽液界面上的蒸汽平均速度；在不同过冷度下Helmholtz极限速度曲线上标注了实验获得的MEB触发温度。如图所示，汽液界面附近的蒸汽计算平均速度和Helmholtz失稳极限速度均随着液相过冷度或壁面过热度的增加而增加。以水作为计算工质时，在不同的液相过冷度下，气相计算平均速度超过Helmholtz极限速度时对应的壁面过热度与实验过的MEB触发温度基本一致。说明Helmholtz失稳可能是导致气膜无法继续稳定存在的原因。

图7　模拟结果与实验值对比

4　结论

本文根据MEB可视化研究结果建立了准稳态下的计算模型，通过引入气泡等效半径对MEB现象触发温度进行了研究，得到如下结论：

（1）在准稳态阶段，在自然对流和表面张力梯度驱动下气膜内形成了一个循环流场。汽液界面处的蒸汽平均速度随着壁面过热度或液相过冷度的升高而升高。

（2）在不同过冷度下，汽液界面处蒸汽平均速度超过Helmholtz失稳极限速度时对应的壁温与实验中获得的MEB触发温度一致，说明Helmholtz失稳可能是导致气膜无法继续稳定存在的原因。

［1］ Shoji M，Yoshihara M．Burnout heat flux of water on a thin wire［C］．Proceeding of 28th National Heat Transfer Symposium of Japan，Japan，1991：121-123．

［2］ Tang J，Mo Z，Sun L，et al．An experimental study on Microbubble Emission Boiling in a subcooled pool：Heat transfer characteristics and visualized presentation［J］．Experimental Thermal and Fluid Science，2017，80：40-52．

［3］ Suzuki K，Inagaki F，Hong C．Subcooled boiling in the ultrasonic field：on the cause of microbubble emission boiling［J］．Heat Transfer Engineering，2011，32（7-8）：673-682．

［4］ Zhu G，Sun L，Tang J，et al．A visualized study of micro-bubble emission boiling［J］．International Communications in Heat and Mass Transfer，2014，59：148-157．

［5］ 邵天，杜亚威，刘燕，等．蒸汽喷射器的三维数值模拟研究［J］．真空科学与技术学报，2014，34（3）：305-311．

［6］ 史立群，杨建道，杨锐，等．耦合末级叶片的汽轮机排汽缸气动数值模拟［J］．动力工程学报，2011，31（9）：655-658．

［7］ 李鹏飞，徐敏义，王飞飞．精通CFD工程仿真与案例实战［M］．北京：人民邮电出版社，2011．

［8］ 彭伟頔，郑乐乐，卢川，等．泡核沸腾两相CFD模拟的参数敏感性分析与模型验证［J］．核科学与工程，2018，38（02）：194-203．

［9］ 唐继国．气泡微细化沸腾现象极其形成机制研究［D］．哈尔滨工程大学，2016．

［10］鲁钟琪．两相流与沸腾传热［M］．北京：清华大学出版社，2002．

［11］唐继国，阎昌琪，孙立成，等．气泡微细化沸腾过程中气泡冷凝破裂现象［J］．化工学报，2014，65（8）：2902-2907．

Simulation Study on Triggering Temperature of Microbubble Emission Boiling

ZHU Guangyu1,2，GUO Yong1，YUAN Yidan1，LIU Yusheng2，LI Wei1

（1. Center for Nuclear Power Safety，China Nuclear Power Engineering Co.，Ltd.，Beijing 100840，China；2. Nuclear and Radiation Safety Center，MEE，Beijing 100082，China）

Due to its extremely high heat transfer capability，Microbubble Emission Boiling（MEB）is considered as the ideal means to promote heat exchanger in nuclear power plant．In this paper，the factor triggering MEB was studied by numerical work and boiling instability analysis．A numerical mode with the consideration of Marangoni stress，heat transfer on the vapor-liquid interface and the thermophysical property of test fluids was built based on the visualized study data．The results showed that，the average velocity near the vapor-liquid interface increases while the wall temperature increases．Furthermore，The wall temperature which the average vapor velocity equals to Helmholtz instability limiting speed is consistent with the temperature triggering MEB in the experiment．Thus，Helmholtz instability may be the reason for the collapsing of vapor film when MEB occurs．

Microbubble emission boiling；Marangoni convection；Numerical simulation；Helmholtz instability

TL334

A

0258-0918（2021）03-0639-05

2020-11-27

国家重点研发计划资助（2018YFB1900100）

朱光昱（1989—），男，黑龙江人，工程师，硕士研究生，现主要从事核电厂严重事故及缓解措施方面研究