基于SP3方法的动力堆中子噪声分析程序研究

龚禾林，陈　长，赵文博，彭星杰，李　庆，于颖锐

基于SP3方法的动力堆中子噪声分析程序研究

龚禾林，陈长，赵文博，彭星杰，李庆，于颖锐

（中国核动力研究设计院 核反应堆系统设计技术国家级重点实验室，四川 成都 610041）

本文基于SP3方程和有限元方法研制了中子噪声分析程序CORCA-NOISE。以国际原子能机构发布的三维压水堆基准例题对程序进行了测试，数值结果表明该程序对通量、eff等稳态参数的计算具有很高的精度。在此基础上基于IAEA 2D基准例题对中子噪声分析进行了初步的计算，给出了在给定输入扰动条件下的中子噪声振幅、相位的空间分布。本程序的研发为下一步深入研究动力堆中子噪声问题打下了基础。

CORCA-PIN；CORCA-NOISE；SP3；中子噪声；有限元

反应堆中子噪声是反应堆内中子通量围绕其稳态平均值存在的随机涨落。按照物理起源的不同，反应堆中子噪声通常分为两类：零功率中子噪声与动力堆中子噪声。零功率中子噪声主要由核反应随机性引发，如每次裂变释放的中子数存在统计涨落等。动力堆中子噪声主要由动力堆堆内构件的振动、冷却剂温度或密度扰动等导致中子宏观截面等参数存在扰动而引发。在高功率系统中，零功率中子噪声相比于动力堆中子噪声而言可以被忽略，且零功率中子噪声的物理机理与数学描述相对清晰，因此动力堆中子噪声研究成为中子噪声相关研究的重点领域。研究噪声的频谱分布不仅可以用于分析相关的反应堆动力学特性，还可以为反应堆的运行监测及故障诊断提供有力支持[1]。

动力堆的噪声分析通常分为频域分析和时域分析两类。时域分析最典型的方法是相关分析，一个信号在不同时间之间的相关程度称为自相关，一对信号在不同时间之间的相关程度称为互相关；对于频域分析，通常将中子学噪声描述成时间的函数，对其进行傅立叶变换后得到噪声的频域表述，一个时间函数可以表示为不同振幅和相位的三角函数的叠加，不同频率对应的振幅构成了噪声的频谱。

本文所述的噪声分析研究，主要致力于寻找反应堆参数扰动的统计特征与中子输运方程求解的中子噪声之间的联系。在这方面，国内外基于扩散方程的有限元法[2-8]、节块法[9-11]，基于中子输运方程的特征线法[12]、离散纵坐标法[13]、蒙特卡洛方法[14, 15]等数值方法开发了不同的中子噪声分析工具软件。此外，Olmo-Jua等基于PARCS和CORE-SIM做了时域—频域综合比较分析[16]。中子噪声分析在燃料弯曲[17, 18]、燃料棒及导向管振动[19]和吊篮振动[20]等方面也有广泛的应用。

SP3方程作为扩散方程的改进和输运方程的近似，在计算精度和速度上相较于输运方程和扩散方程取得了很好的平衡，中国核动力研究设计院基于SP3方程自主研制了pin-by-pin级的CORCA-PIN堆芯物理计算程序，兼具稳态和瞬态计算功能。本文基于SP3方程和有限元方法研制了中子噪声分析程序。利用国际原子能机构（IAEA）发布的三维压水堆基准例题对程序进行了通量、eff等稳态参数的计算能力的测试，结果表明程序对典型稳态参数的计算具有较高的精度。在此基础上进行了中子噪声频谱计算，给出了给定频点下的噪声分布。

1　控制方程

考虑双群模型的含时SP3输运方程为：

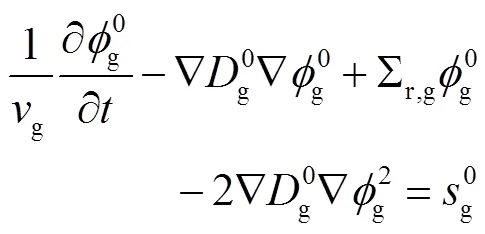
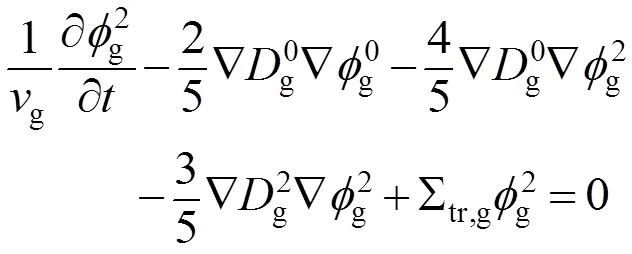
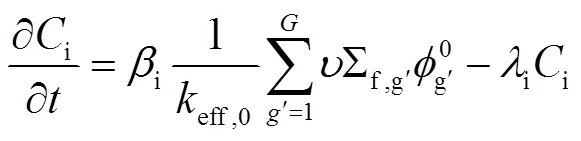
其中，

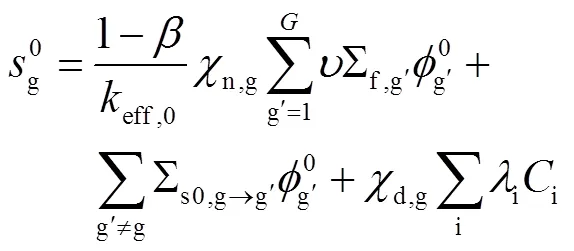
针对上述方程作一阶微扰并略去二阶项，进行傅立叶变换后有：

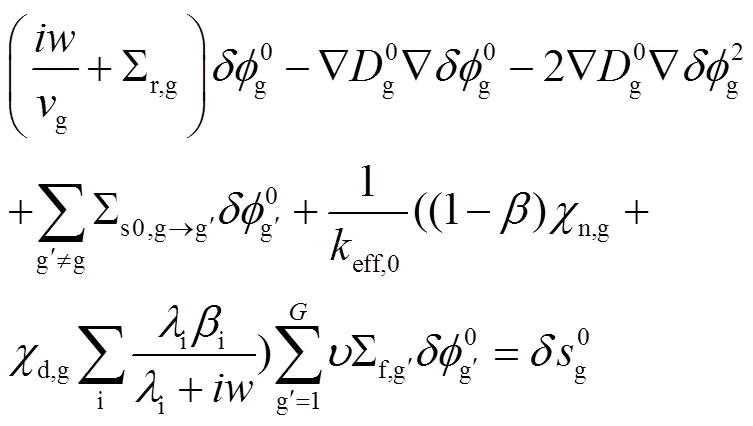
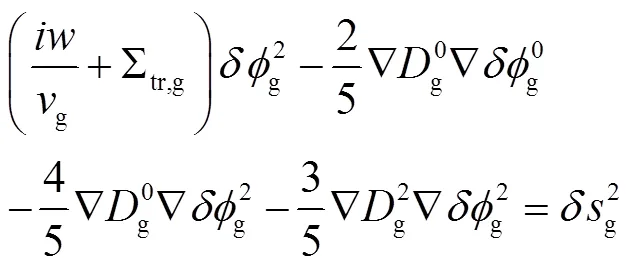
其中，

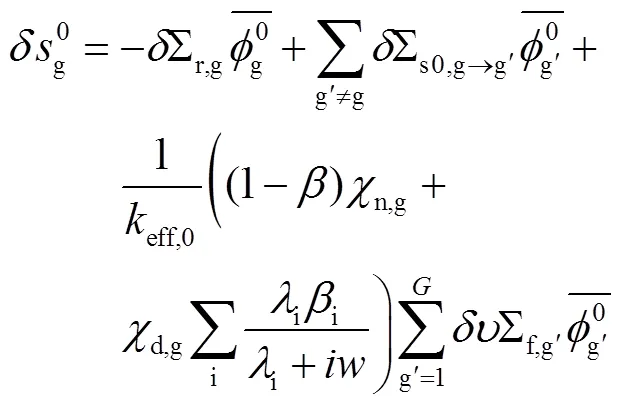
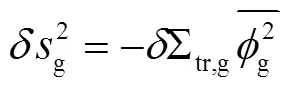
2　程序结构

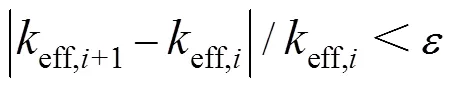
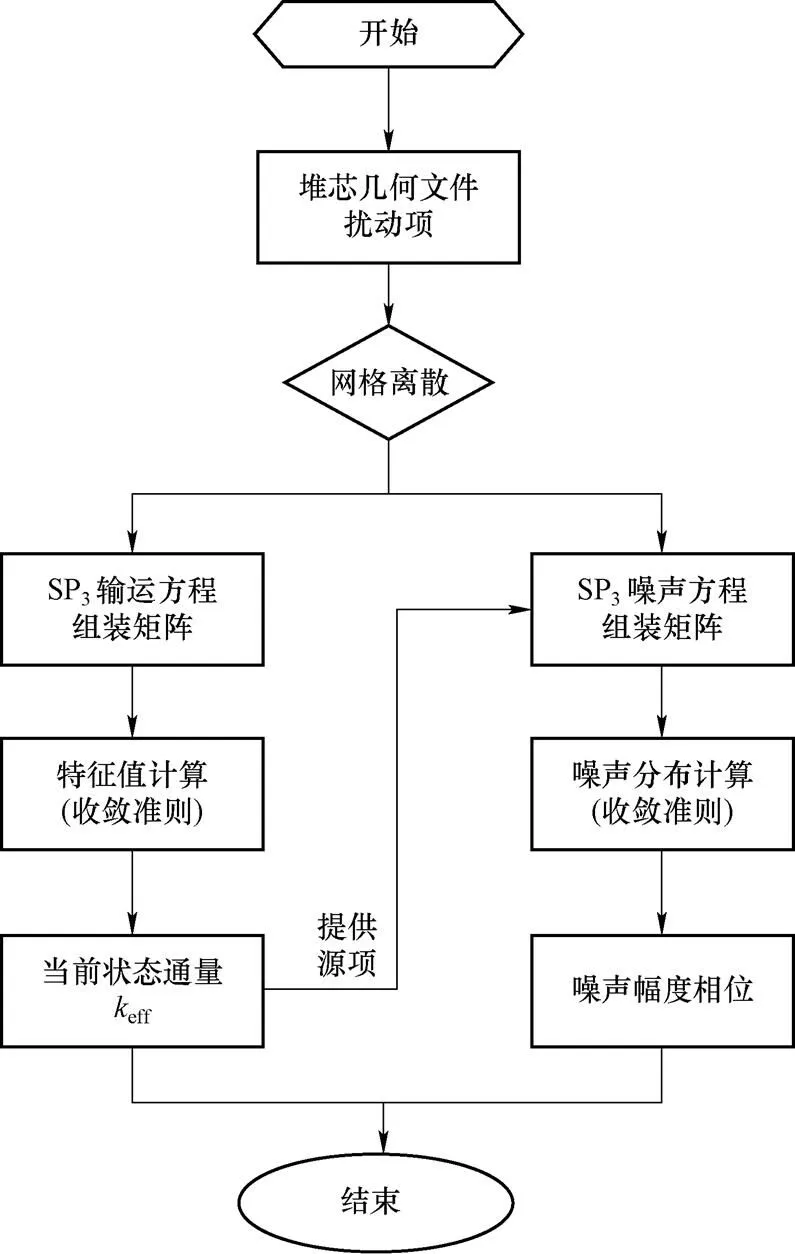
图1　CORCA-NOISE程序结构图

3　二维基准例题测试

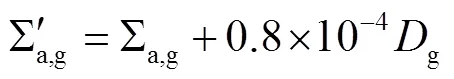
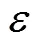
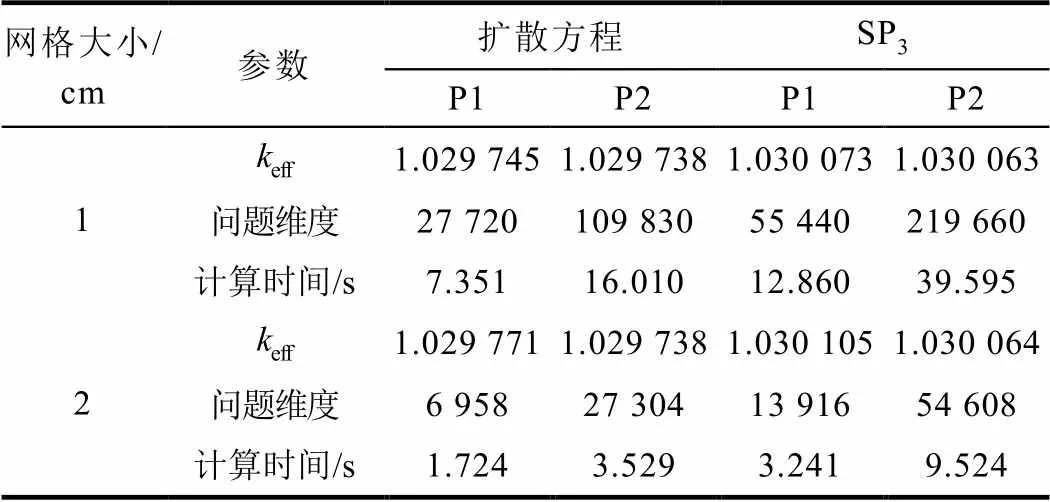
表1　keff的计算结果

4　反应堆中子噪声计算

4.1　IAEA 2D 基准例题

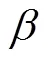
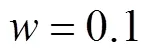
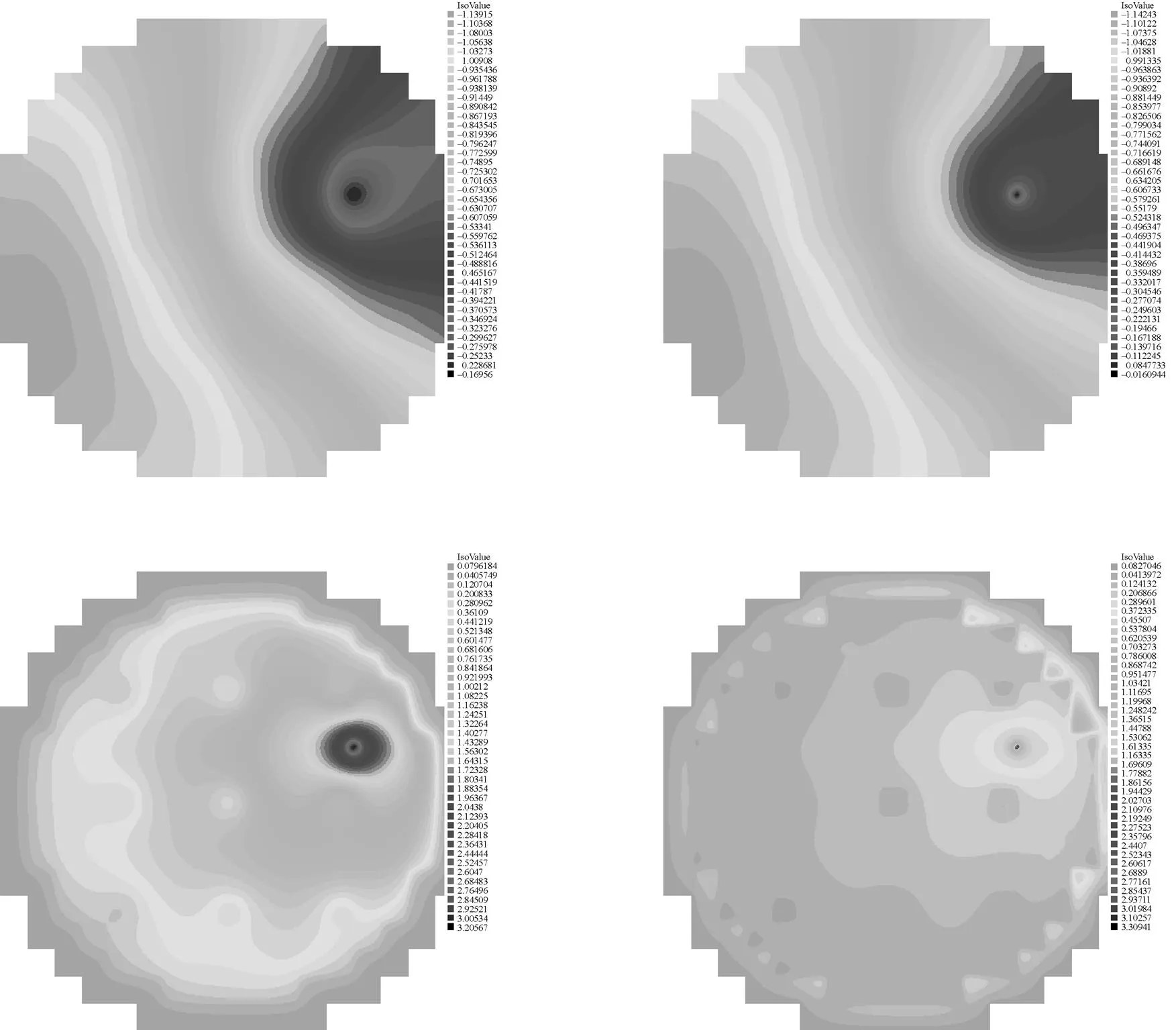
图2　扰动区域[89, 90] cm×[39, 40] cm，频率w=0.1 Hz对应的快（左）、热（右）群中子噪声相位（上）、振幅（下）

图3　扰动区域[80, 100] cm×[20, 40] cm，频率w=0.1 Hz对应的快（左）、热（右）群中子噪声相位（上）、振幅（下）

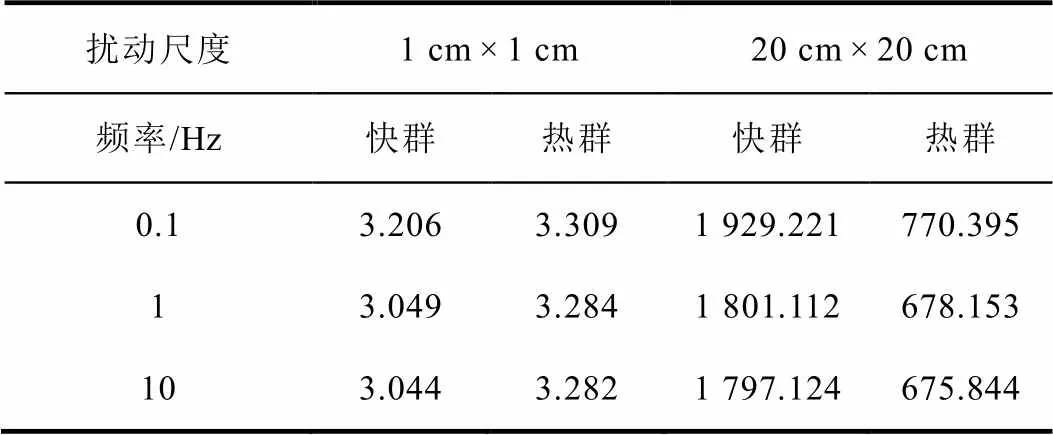
表2　中子噪声最大振幅值

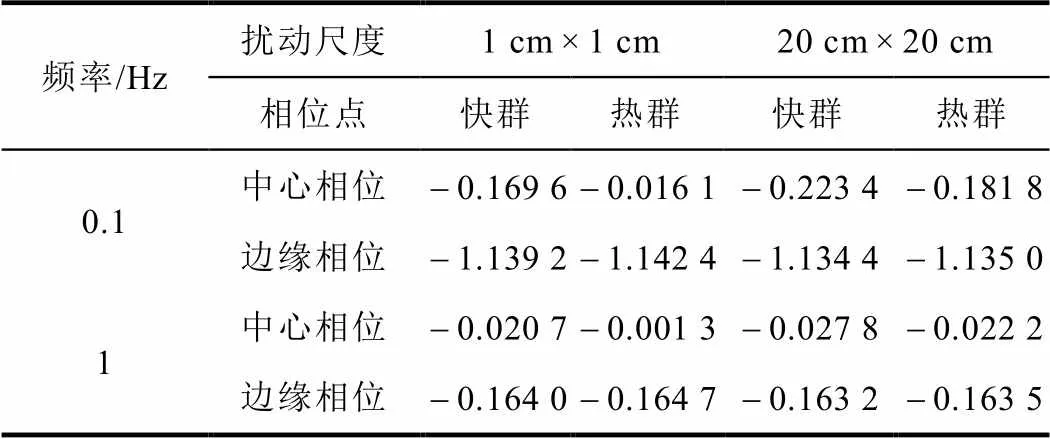
表3　中子噪声相位

续表

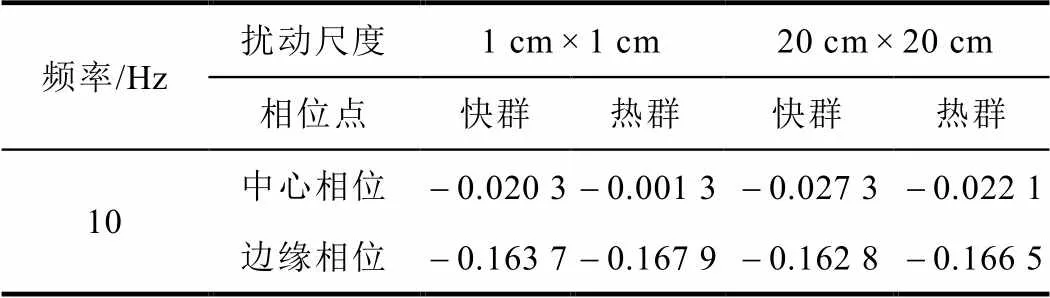
频率/Hz扰动尺度1 cm × 1 cm20 cm × 20 cm 相位点快群热群快群热群 10中心相位 - 0.020 3 - 0.001 3 - 0.027 3 - 0.022 1 边缘相位 - 0.163 7 - 0.167 9 - 0.162 8 - 0.166 5

4.2　MOX 2D 基准例题

为了比较扩散方程和SP3方程在中子噪声分析计算中的差异，我们采用第1节介绍的计算方法，对2D MOX基准例题进行了中子噪声频谱计算。选取Brantley 和 Larsen 在文献［24］中给出的2D MOX 基准例题进行了SP3计算与扩散计算的对比验证测试。该例题堆芯布置可参见文献［24］，材料参数参见文献［25］。我们采用每个组件44×44网格剖分，P1有限元，相关的eff和功率分布计算结果见图4。其中，参考解来文献［25］中给出的SN16，网格划分为每个组件132×132网格。可以发现，CORCA-NOISE在进行稳态计算时，求解SP3和扩散方程均具有很高的计算精度。

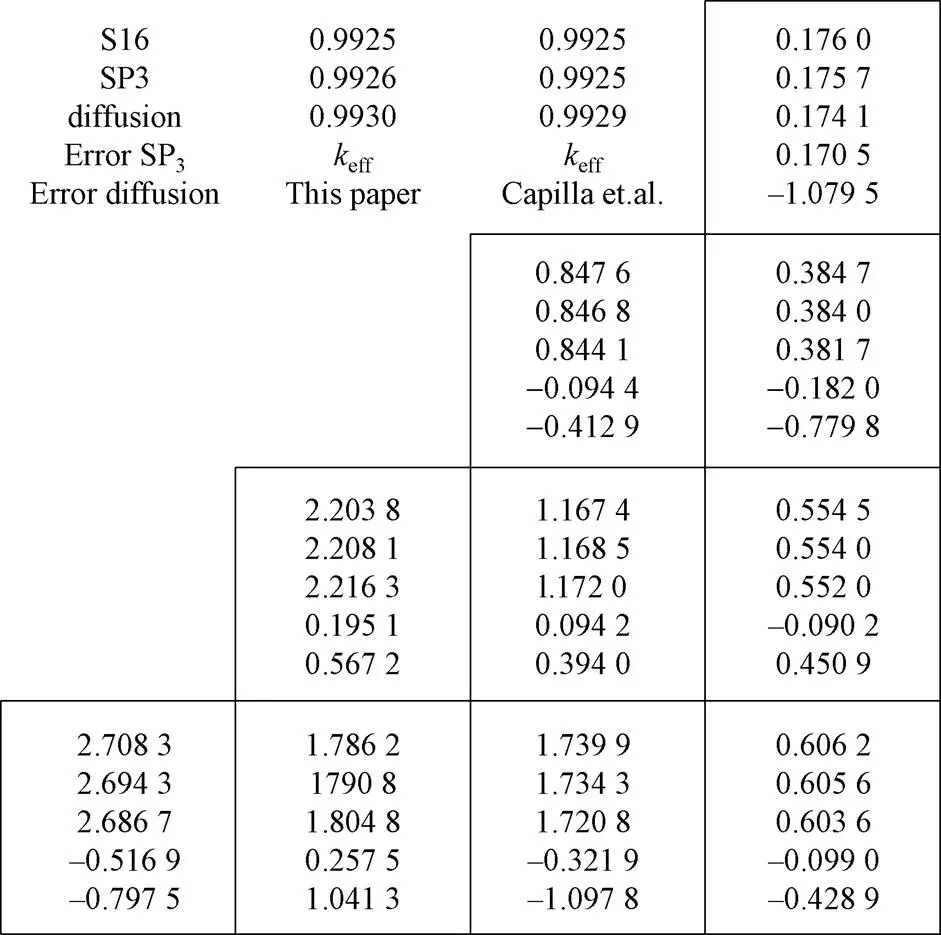
图4　2D MOX 基准例题keff和组件功率分布计算结果比较

可以发现，SP3方程与扩散方程所计算的中子噪声分布总体上一致，但是由于SP3方程是对扩散方程的改进，所计算的中子噪声分布有定量差异。详细的数值分析显示，SP3方程所计算的噪声幅度总体上比扩散方程的计算幅度高10%～20%。此外，由于快群中子速度更高，中子噪声空间分布亦比较平滑，热群噪声分布则受MOX和UO2组件排列的影响，显示出明显的棋盘式分布特性。由于在反应堆内部可安装的中子探测器极为有限，为了对反应堆内中子噪声进行更准确的描述，采用输运近似计算计算中子噪声相比于目前主流的扩散计算更为必要。

此外，图5和图6中通过扩散方程和SP3方程给出的中子噪声频率空间分布，与文献［26］通过扩散方程和SN方程给出的中子噪声分布，形状上是一致的，虽然本文没有将SN计算结果（需再单独编写程序）进行直接比较，但分布上的一致性也间接证明了本文提供的SP3中子噪声方程求解的合理性。关于SP3中子噪声方程的正确性的进一步验证，将是后续研究的重中之重。

通过图5和图6我们还发现，无论是采用扩散方程还是SP3方程，快群噪声源引起的噪声热群噪声幅度较快群噪声幅度低近一个量级；另一方面，热群噪声源引起的快群噪声幅度和热群噪声幅度相当。这是因为，热群噪声对裂变源项影响更为直接，通过裂变作用，下一代中子噪声对快群和热群的影响在数量级上保持一致。快群噪声源则不然，其对快群噪声是直接的，需要经过慢化才能将噪声效应传递到热群，因此体现出了量级上的差异。

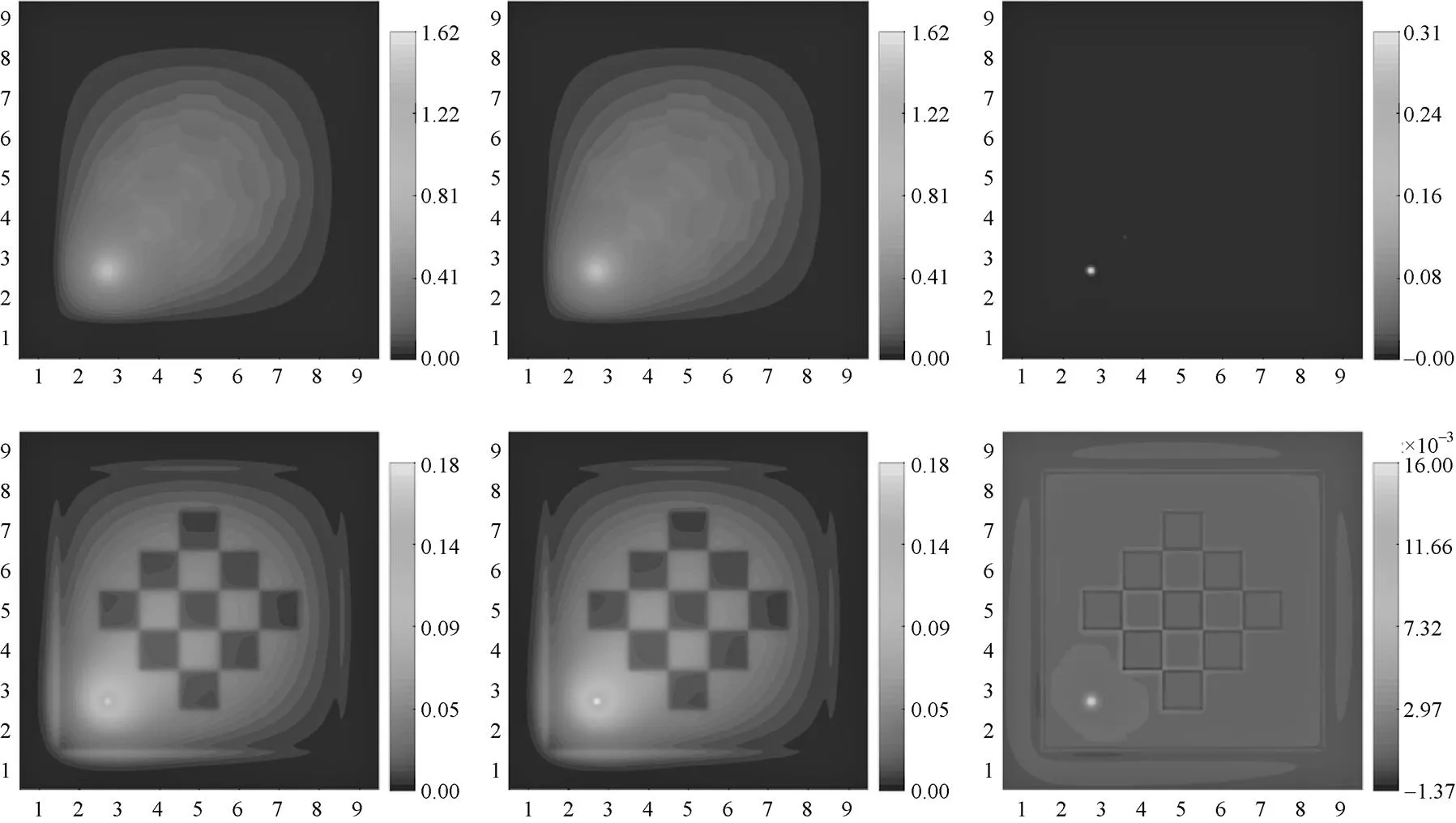
图5 MOX问题（47.34 cm, 47.34 cm）处快群点噪声源的快群（上）和热群（下）噪声幅度分布。

左：扩散方程计算；中：SP3方程计算；右：SP3方程与扩散方程结果的差异

Fig.5 The amplitude distribution of the fast (top) and thermal (bottom) noise arise from point noise source of fast group at (47.34 cm, 47.34 cm). Left: diffusion approximation; middle: SP3approximation; right: the difference between diffusion and SP3approximation

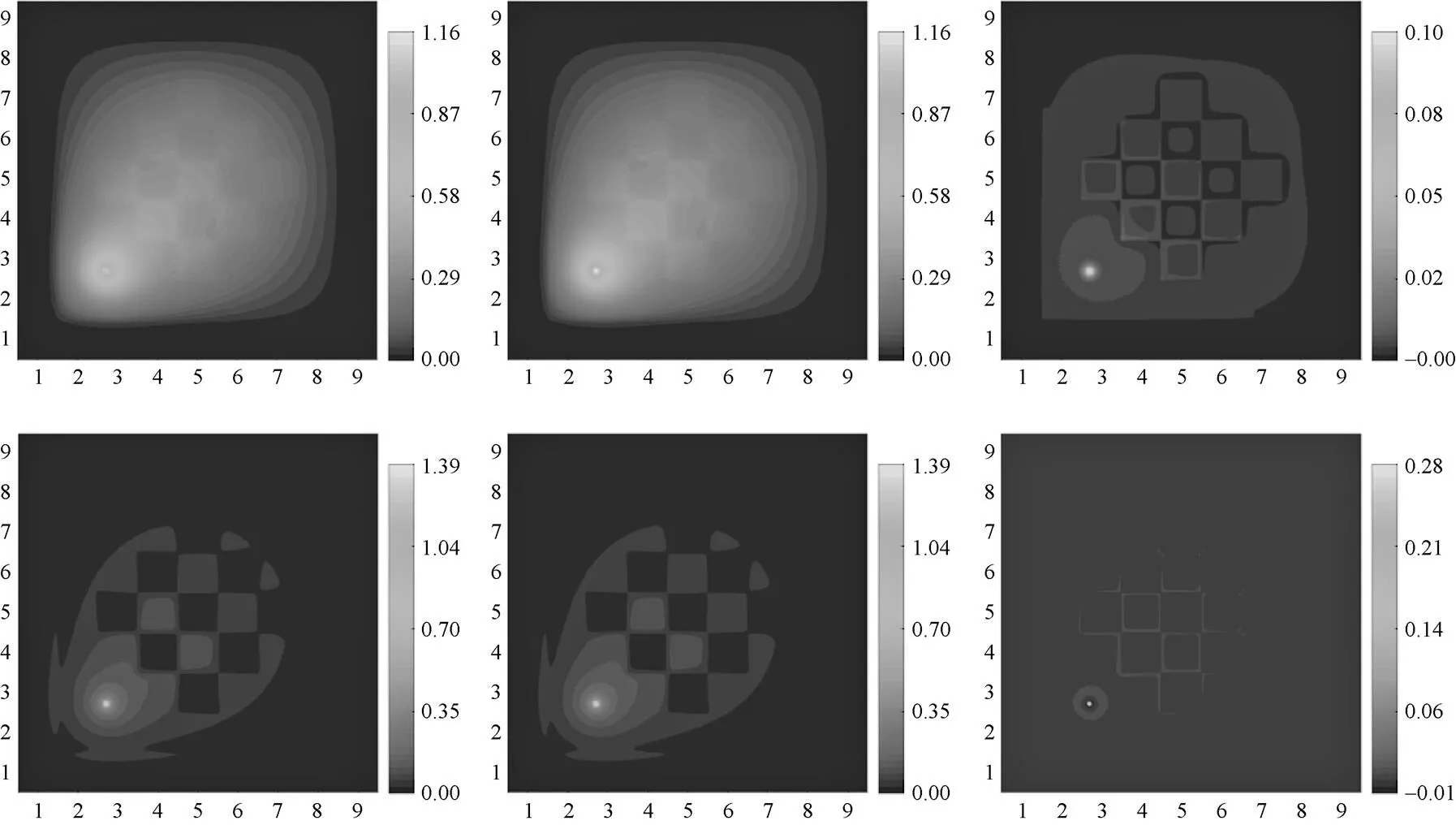
图6 MOX问题（47.34 cm, 47.34 cm）处热群点噪声源的快群（上）和热群（下）噪声幅度分布。

左：扩散方程计算；中：SP3方程计算；右：SP3方程与扩散方程结果的差异

Fig.6 The amplitude distribution of the fast (top) and thermal (bottom) noise arise from point noise source of thermal group at (47.34 cm, 47.34 cm). Left: diffusion approximation; middle: SP3approximation; right: the difference between diffusion and SP3approximation

5 结论与展望

本文开发了基于SP3方程和有限元方法的中子噪声分析程序CORCA-NOISE，使用压水堆基准例题和MOX基准例题进行了eff和功率分布数值校验。计算结果表明，本文采用的计算方法以及程序针对稳态计算结果是可信的。数值计算结果表明，扩散近似和SP3近似给出的中子噪声分布在噪声源处有明显差异。由于在反应堆内部可安装的中子探测器极为有限，为了对反应堆内中子噪声进行更准确的描述，采用输运近似计算中子噪声相比于目前主流的扩散计算更为必要。此外，通过给定扰动参数、扰动区域、扰动强度和频率，利用本程序可实现中子噪声空间分布计算，可计算扫描得到用户关心的特定频段的中子噪声频谱，实现基于反应堆的中子噪声分析理论和实验探索，为反应堆的运行监测和故障诊断提供理论输入。下一步将在频谱分析以及CORCA堆芯物理计算程序框架下的并行扩展方面进一步开展工作。

［1］ 罗璋琳．核动力堆噪声分析［M］．北京：中国原子能出版社，2013．

［2］ 袁宝新，杨万奎，曾和荣．基于ICEM-CFD的核噪声分析用有限元程序研究［J］．原子核物理评论，2017，34（3）：677-681．

［3］ Tran H N，Zylbersztejn F，Demazière C，et al．A multi-group neutron noise simulator for fast reactors［J］．Annals of Nuclear Energy，2013，62：158-169．

［4］ Hosseini S A，Vosoughi N．Neutron noise simulation by GFEM and unstructured triangle elements［J］．Nuclear engineering and design，2012，253：238-258．

［5］ Demaziere C．CORE SIM：A multi-purpose neutronic tool for research and education［J］．Annals of Nuclear Energy，2011，38（12）：2698-2718．

［6］ Hosseini S A．High accurate three-dimensional neutron noise simulator based on GFEM with unstructured hexahedral elements［J］．Nuclear Engineering and Technology，2019，51（6）：1479-1486．

［7］ Hosseini S A，Vosoughi N，Vosoughi J．Neutron noise simulation using ACNEM in the hexagonal geometry［J］．Annals of Nuclear Energy，2018，113：246-255．

［8］ Mylonakis A G，Vinai P，Demazière C．Numerical solution of two-energy-group neutron noise diffusion problems with fine spatial meshes［J］．Annals of Nuclear Energy，2019：107093．

［9］ Viebach M，Bernt N，Lange C，et al．On the influence of dynamical fuel assembly deflections on the neutron noise level［J］．Progress in Nuclear Energy，2018，104：32-46．

［10］ Chionis D，Dokhane A，Belblidia L，et al．Simulate-3k analyses of neutron noise response to fuel assembly vibrations and thermal-hydraulics parameters fluctuations［C］Int．Conf．Mathematics & Computational Methods Applied to Nuclear Science & Engineering（M&C 2017），Jeju，Korea．2017．

［11］ Viebach M，Lange C，Bernt N，et al．Simulation of low-frequency PWR neutron flux fluctuations［J］．Progress in Nuclear Energy，2019，117：103039．

［12］ Gammicchia A，Santandrea S，Zmijarevic I，et al．A MOC-based neutron kinetics model for noise analysis［J］．Annals of Nuclear Energy，2020，137：107070．

［13］ Bahrami M，Vosoughi N．SN transport method for neutronic noise calculation in nuclear reactor systems：Comparative study between transport theory and diffusion theory［J］．Annals of Nuclear Energy，2018，114：236-244．

［14］ Rouchon A，Zoia A，Sanchez R．A new Monte Carlo method for neutron noise calculations in the frequency domain［J］．Annals of Nuclear Energy，2017，102：465-475．

［15］ Yamamoto T．Implementation of a frequency-domain neutron noise analysis method in a production-level continuous energy Monte Carlo code：Verification and application in a BWR［J］．Annals of Nuclear Energy，2018，115：494-501．

［16］ Olmo-Juan N，Demazière C，Barrachina T，et al．PARCS vs CORE SIM neutron noise simulations［J］．Progress in Nuclear Energy，2019，115：169-180．

［17］ Yamamoto A，Endo T，Nagano H，et al．A simple treatment of increased gap due to fuel assembly bowing through correction of cross sections［J］．Journal of Nuclear Science and Technology，2019，56（6）：471-478．

［18］ Fetterman R J，Franceschini F．Analysis of PWR assembly bow［J］．2008．

［19］ Mylonakis A G，Demaziere C，Vinai P，Lamirand V，Rais A，Pakari O，Frajtag P，Godat D，Hursin M，Perret G，Laureau A，Fiorina C，Pautz A．（2020）．CORE SIM+SIMULATIONS OF COLIBRI FUEL RODS OSCILLATION EXPERIMENTS AND COMPARISON WITH MEASUREMENTS［C］．Proc．PHYSOR 2020．

［20］杨泰波，刘才学，罗婷，等．基于中子噪声分析的某核电厂堆芯吊篮梁型振动特征研究［J］．核科学与工程，2017，37（1）：42-47．

［21］ Frey P．Medit：An interactive mesh visualization software［J］．2001．

［22］ Lehoucq R B，Sorensen D C，Yang C．ARPACK users' guide：solution of large-scale eigenvalue problems with implicitly restarted Arnoldi methods［M］．Siam，1998．

［23］ Lee R R．Argonne Code Center：Benchmark Problem Book［J］．Report No．：ANL-7416，Supp，1976，2：277-466．

［24］ Brantley，P．S．，Larsen，E．W．，2000．The Simplied P3 Approximation．Nuclear Science and Engineering 134（1），1-21．

［25］ Capilla，M．，Talavera，C．，Ginestar，D．，Verdu，G．，2008．A nodal collocation approximation for the multi- dimensional PL equations-2D applications．Annals of Nuclear Energy 35（10），1820-1830．

［26］ Bahrami，M．，Vosoughi，N．，2018．SN transport method for neutronic noise calculation in nuclear reactor systems：Comparative study between transport theory and di↵usion theory．Annals of Nuclear Energy 114，236 – 244．

Development of a Neutron Noise Simulator with SP3Approximation

GONG Helin，CHEN Zhang，ZHAO Wenbo，PENG Xingjie，LI Qing，YU Yingrui

（Nuclear Power Institute of China Science and Technology on Reactor System Design Technology Laboratory，Chengdu of Sichuan Prov.610041，China）

In this paper，the development of a neutron noise simulator CORCA-NOISE is reported which is based on the SP3approximation and the finite element method.The SP3approximation of the neutron transport equation allows improving the accuracy for both static and transient simulations for reactor core analysis compared with the neutron diffusion theory.Typical steady state parameters，i.e.，the neutron flux andeff，are calculated with high accuracy.Finally，the distribution of the neutron noise and the spectrum are calculated for the PWR IAEA 2D benchmark problem.The noise amplitude and the phase distribution under given frequency is given.

CORCA-PIN；CORCA-NOISE；SP3；Neutron noise；Finite element method

TL48

A

0258-0918（2021）03-0491-09

2020-03-02

国家自然科学基金资助项目（11905216）

龚禾林（1987—），男，重庆潼南人，高级工程师，博士，现主要从事反应堆物理与数据科学方面研究