基于邻介熵和邻度熵的复杂网络中心性算法
卢鹏丽, 周 庚
(兰州理工大学 计算机与通信学院, 甘肃 兰州 730050)
近年来,复杂网络的研究在航空线路、电网、社交网络、生物网络、生态网络等领域受到了广泛的关注[1-6].网络的无标度特性[7]和小世界特性[8]使得网络中的一些重要节点对网络的结构和功能有很大影响.当这些节点在网络中出现故障时,它们的影响将迅速扩散到整个网络.因此,如何准确量化复杂网络中节点的重要性,找出关键节点,具有重要的理论和现实意义[9].例如,控制疾病网络中的关键节点能有效防止病毒的大规模传播[10];社交网络中控制关键节点将有助于阻止谣言的扩散[11];准确找到电力网络的重要节点,对其加以重点监管和保护,可使得电力传输顺利进行,有效防止大面积停电事故的发生[12];识别和控制交通网络中的重要节点能有效解决交通拥堵的问题.针对复杂网络中节点重要性的评价,学者们提出了度中心性(DC)[14]、 接近中心性(CC)[15]、介数中心性(BC)[16]、特征向量中心性(EC)[17]、子图中心性(SC)[18]、谱密度中心性[19]和K-core中心性(KC)[20]等方法.
在信息论里,熵被用于表示事物的不确定性,熵值越大,表示可以传递的信息量越大.图的熵首先由mowshowitz和Trucco引入,并被广泛地用于描述网络的拓扑结构.近年来,图论学者对不同的信息熵函数进行研究,发现图熵可用来表示复杂网络中节点的中心性.传统上,香农熵(Shannon entropy)、冯诺依曼熵(von Neumann entropy)可用来分析网络的整体统计特性,当删除网络中的一条边,网络的熵会随之减小.因此可以考虑在网络中用删除部分节点和与它相连的边对整个网络的熵的影响来反映节点的重要性,或者可以考虑在网络中指定节点上添加边,使得节点的度最大化,从而体现节点在网络中的重要性[21].Simmons等[22]发现冯诺依曼熵可以用来约束图的泰尔指数,并提出一种基于图的泰尔指数和冯诺依曼指数的节点重要性度量措施.Massimo等[23]引入距离熵作为复杂网络中给定节点与其相邻节点之间路径长度分布均匀性的度量措施,并将距离熵与接近中心性耦合,提出一种基于距离熵的节点中心性度量措施.聂廷远等[24]提出了映射熵(ME)和局部熵(LE)两种攻击策略来识别复杂网络中的重要节点.
虽然已有的中心性准则得到了广泛的应用,但也存在不足.度中心性DC和介数中心性BC都只考虑了节点vi的所有邻居节点对节点自身的重要性的影响,并没有考虑哪一部分邻居节点集对节点vi自身的重要性影响更大.本文将节点vi的邻居节点集划分成关联邻居节点集MR和非关联邻居节点集MUR,在此基础上提出了关联邻居中心性RNC和非关联邻居中心性URNC.采用动态攻击的方式[25],通过在一种人工网络和五种实际网络上进行仿真实验.结果表明,与传统的中心性准则相比,新的中心性指标RNC 能够得到更准确、更全面的结果.
1 相关研究和本文算法
1.1 相关研究
传统的节点中心性问题主要分为基于邻居信息的节点中心性研究、基于经过节点最短路径数目的节点中心性研究和基于节点移除以及收缩的节点中心性研究[27].基于邻接信息节点中心性研究主要关注的是网络节点本身的信息及其邻居节点的信息;基于经过节点的最短路径数目的节点中心性研究主要是考虑信息流在网络中的传播;基于节点的移除和收缩的节点中心性研究侧重于研究节点删除和收缩过程中网络拓扑结构发生的变化.
设网络G=(V,E),其中V={v1,v2,…,vN}为其节点集,E={e1,e2,…,eL}为其边集,节点数为N,边数为L,di为节点vi的度.
1) 度中心性.复杂网络中节点的度中心性表示的是一个节点邻居的个数占总节点数的比例,最直观地认为邻居越多,节点就越重要.复杂网络中节点的度中心性定义为
DCi=di/(N-1)
(1)
2) 介数中心性.节点的介数中心性是指网络中经过该节点的最短路径的数目占该网络中最短路径总数的比例.节点v的介数中心性定义为
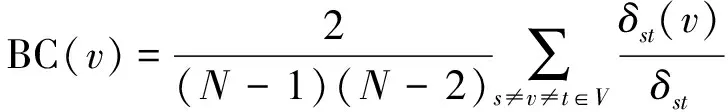
(2)
其中:δst(v)表示网络中从任意节点s到节点t且经过节点v的最短路径的条数;δst表示网络中从任意节点s到节点t的最短路径的条数.
3) K-core中心性.节点的K-core中心性是根据节点的位置度量节点影响力.K-core分解算法通过迭代删除节点,给网络中所有节点赋予K-core值.算法思想如下:首先,从图中删除所有度为1的节点以及相关的连边,若剩下的节点里,仍有度值为1的节点,则重复上述操作,直到图中所有节点的度值都大于1,然后将所有删除的节点的K-core值记为1,即这些节点均处于K-core值为1的层;其次,删除度为2的节点,直到没有度为2的节点,然后将所有删除的节点的K-core值记为2,这个过程一直持续到所有节点都删除为止,即每个节点独有对应的K-core值.显然,K-core值越大的节点越接近网络的中心位置,节点影响力也就越大.
4) 特征向量中心性.节点vi的特征向量中心性是节点在网络对应的邻接矩阵中主特征向量的第i个分量的值.特征向量中心性(eigenvector centrality,EC)被定义为
EC(vi)=αmax(vi)
(3)
其中:αmax是对应于邻接矩阵A的最大特征值的特征向量;αmax(vi)是特征向量对应的第i个分量.
5) 基于熵的节点中心性.在复杂网络中,为了便于计算,节点的重要性定义为
(4)
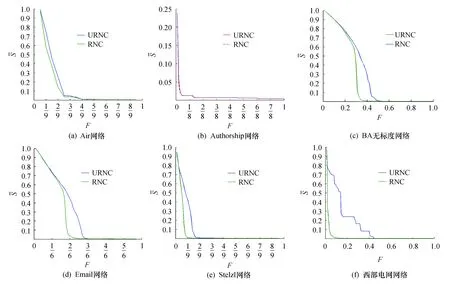
其中:ki代表一个节点在网络中的一些不变量,例如节点的度、节点的介数等,且0 图(网络)的熵定义为 (5) 图熵反映图的整体特性,为了研究节点的特性,基于图熵,学者们针对节点及邻居节点构成的子图提出了局部熵和交叉熵,这为后来熵中心性指标的研究奠定了坚实的基础.局部熵(localEnt)和交叉熵(crosEnt)的节点重要性定义如下[28]: (6) (7) 其中:M表示节点vi的邻居节点集的大小;Ii是节点vi的重要性;Ij是节点vi邻居节点的重要性;局部熵localEnti是节点vi所有邻接点的信息熵,即一个节点的重要性由其邻居节点的信息反映;交叉熵crosEnti由节点vi及其邻居节点的信息共同反映. 基于以上的研究基础,Nie[24]提出了基于度中心性的局部熵(LE)和映射熵(ME)中心性: (8) (9) 其中:DCi为节点vi的度中心性;M为节点vi邻居节点集的大小;DCj为节点vi的邻居节点集M中的节点vj的度中心性. 复杂网络中节点的度中心性表示的是一个节点vi的邻居节点占节点总数的比例,相邻节点越多,节点就越重要.节点vi的介数中心性是指网络中经过该节点的最短路径的数目占该网络中最短路径总数的比例,经过节点vi的最短路径一定经过其邻居节点.然而度中心性和介数中心性都只考虑了节点vi的所有邻居节点对其重要性的影响,并没有考虑那一部分邻居节点集对节点vi自身的重要性影响更大. 本文将节点vi的邻居节点集进一步进行划分,将邻居节点集划分成关联邻居节点集MR(节点vi的邻居节点集中的节点vk彼此之间有边的节点对组成的节点集称之为关联邻居节点集)和无关联邻居节点集MUR(节点vi的邻居节点集中的节点vj彼此之间没有边的节点对组成的节点集称之为无关联邻居节点集),受局部熵中心性(LE)和映射熵中心性(ME)的启发,通过计算节点vi自身的DC和BC及其关联邻居节点集MR和无关联邻居节点集MUR中各节点的DC和BC之和,提出了关联邻介熵NBER、非关联邻介熵NBEUR、关联邻度熵NDER和非关联邻度熵NDEUR.结合关联邻介熵NBCR和关联邻度熵NDCR提出了关联邻居中心性RNC.结合非关联邻介熵NBCUR和非关联邻度熵NDCUR提出了非关联邻居中心性URNC.关联邻介熵NBER、非关联邻介熵NBEUR、关联邻度熵NDER和非关联邻度熵NDEUR定义如下: (10) (11) (12) (13) 其中:DCi为节点vi的度中心性;BCi为节点vi的介数中心性;MR为节点vi关联邻居节点集;NMR为节点vi关联邻居节点集的节点个数;MUR为节点vi非关联邻居节点集;NMUR为节点vi非关联邻居节点集的节点个数. 关联邻居中心性RNC和非关联邻居中心性URNC定义如下: 本实验的实验平台为联想G500个人笔记本电脑,处理器为Corei5-3230,运行内存为8 G;软件开发平台为MATLAB R2014 a. 本文通过一种人工网络模型和五种实际网络模型进行仿真实验,来评估新中心性度量措施的有效性.其中人工网络为BA 无标度网络,是由Pajek软件生成,生成参数设置如下:节点总数N=2 000,初始顶点数N0=10,初始连边概率α=0.25.五种实际网络分别为Air美国航空网络、Authorship科学家协作网络、Email 网络、Stelzl 网络和西部电网网络[26],网络的部分参数见表1. 表1 六种网络的部分参数特性 本文使用最大连通子图的相对大小作为节点重要性评价标准.连通子图指的是存在于网络的一个子图,在这个子图内,任意两个节点之间都至少存在一条简单路径.对于非连通的图,可以将其分解成两个或者两个以上的联通分支.其中各连通分支中包含节点最多的分支称为最大连通分支,也称为最大连通子图.网络会随着中心节点的移除而分裂成若干个不连通的子图,其中最大连通子图的节点个数和网络的整体结构密切相关,最大连通子图的节点个数越少,就代表网络被损毁得越严重.最大连通子图相对大小被定义为 (16) 本文以网络最大连通子图的相对大小作为复杂网络抗毁性评价标准,全面地分析了新中心性度量措施排序效果. Step1:使用Pajek软件通过设置特定生成参数生成BA无标度网络.net文件,并把BA无标度网络和其余五种实际网络的.net文件在Matlab中进行处理,生成对应的邻接矩阵. Step2:计算六种实验网络下各节点对应的关联邻居中心性RNC(i)和非关联邻居中心性URNC(i)的值,并按照从大到小的顺序依次排序. Step3:根据上述排序结果每次删除前20个节点,然后计算一次网络的最大连通子图的相对大小,重复上述操作,直到将网络中所有节点都被删除(当网络中剩余节点不足20 个时按照20个计算,并进行一次删除操作).最终将生成的最大连通子图相对大小的序列进行曲线拟合来反映各指标的攻击效果,并对比各网络下关联邻居中心性RNC 和非关联邻居中心性URNC二者的效果,选出二者中攻击效果最佳的攻击方式用于后续的新中心性度量措施与传统中心性度量措施对比实验. Step4:计算六种实验网络下各节点对应的介数中心性BC(i)、度中心性DC(i)、K-core中心性KC(i)、特征向量EC(i)的值,并按照从大到小顺序依次排序.按照步骤Step3中删除节点的方式生成对应的最大连通子图相对大小的序列,将Step3中筛选出的攻击效果最佳的新指标与上述五种传统中心性指标进行对比实验,分析各指标的攻击效果. Step5:算法结束. 在这组实验中,将节点vi的邻居节点集划分成关联邻居节点集和无关联邻居节点集,通过对比六种网络模型在关联邻居中心性RNC和非关联邻居中心性URNC两种指标的攻击效果(如图1和表2所示),分析新的攻击策略对网络的破坏性. 表2 利用RNC和URNC动态攻击时各网络最先达到特定最大连通子图相对大小的指标 图1表示的是关联邻居中心性RNC和非关联邻居中心性URNC动态攻击下的对比实验.所谓的攻击效果好就是在删除同样比例的节点后,剩余网络的最大连通子图的相对大小越小越好. 1) 从图1a可看出,整个过程中关联邻居中心性RNC均比非关联邻居中心性URNC攻击效果好. 图1 RNC和URNC动态攻击效果对比Fig.1 RNC and URNC dynamic attack effect comparison 2) 在图1b中,由于Authorship网络的初始最大连通子图相对大小是0.25,所以纵坐标最高值为0.25.当0.2 3) 从图1c可以看出,非关联邻居中心性URNC明显优于关联邻居中心性RNC,由于BA无标度网络的生成过程中,新增节点优先于度大的节点连接,因此,关联邻居节点集明显小于非关联邻居节点集的大小,所以在动态攻击的情况下URNC攻击效果明显优于RNC. 4) 从图1d和图1f中可以看出,当0.8 5) 从图1e可以看出,当0.7 实验结果表明,在六个网络中,关联邻居中心性RNC明显优于非关联邻居中心性URNC. 从表3和图2可以看出: 表3 动态攻击下各网络最先达到特定最大连通子图相对大小的指标 图2 动态攻击下各网络最先达到特定最大连通子图相对大小的指标 6) 在西部电网网络中,RNC明显优于其他四种攻击方式. 从表4可以看出: 表4 动态攻击下删除一定比例节点后网络的 1) 在Air网络中,当0.1 2) 在Authorship中,当0.02 3) 在BA无标度网络中,当0.3 4) 在Email网络中,当0.3 5) 在Stelzl网络中,0.1 6) 当0.1 从表5可以看出,相比于其他四种中心性算法,RNC和URNC的时间复杂度相对较高.从刻画节点重要性的范围以及适用的网络范围来看,RNC和URNC相比其他四种算法,能得到较全面、较精确的结果,且适用范围更广泛. 表5 各算法性能对比 本文将节点的邻居节点集进一步进行划分,将邻居节点集划分成关联邻居节点集和无关联邻居节点集,并基于图熵的特性提出了新的节点中心性度量措施,即基于邻介熵(NBE)和邻度熵(NDE)的关联邻居中心性RNC和非关联邻居中心性URNC.实验结果表明,当在动态攻击的方式下,新的中心性RNC度量措施在除BA无标度网络外的其他五种网络上,明显优于其他传统的节点中心性度量措施,而在BA无标度网络上,新的中心性URNC度量措施明显优于其他传统的节点中心性度量措施. 总体而言,美国航空网络、作家协作网、Email网络、Stelzl网络、美国西部电网网络比演化网络BA无标度网络模型更脆弱.关联邻居中心性RNC新的组合从节点邻居和全局两个方面考虑节点的中心性,在六个网络中表现良好,相较于其他传统节点中心性,新节点中心性指标对节点重要性的刻画更全面、更精确.1.2 基于邻介熵和邻度熵的复杂网络中心性算法
2 实验及结果分析
2.1 实验数据

2.2 抗毁性测度
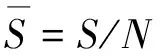

2.3 实验流程


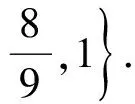
2.4 关联邻居中心性RNC和非关联邻居中心性URNC对比实验结果分析

2.5 新组合中心性度量措施与传统中心性度量措施对比实验结果分析



2.6 各算法性能对比

3 结论

