不同方向外电场下SiF2分子激发特性

梁冬梅, 黄 意, 陈 亮, 曾凡菊, 孙光宇, 荆 涛

(1. 凯里学院 理学院, 贵州 凯里 556011; 2. 凯里学院 大数据工程学院, 贵州 凯里 556011; 3. 贵州师范学院 物理与电子工程学院, 贵州 贵阳 550018)

早在19世纪50年代，SiF2一直受到研究者的广泛关注.这些研究主要集中在SiF2气体的光谱检测，包括紫外吸收光谱、微波光谱和红外光谱的检测[1-4].由于制备SiF2气体的原料短缺，SiF2气体的实验研究基本上没有.目前大多是关于SiF2气体的理论计算和模拟.例如，江文世等[5]计算了SiF2分子基态的结构与热力学性质.Helluy等[6]从实验和理论模拟上研究了氟硅化合物中Si和F原子的核磁共振光谱.赵俊等[7]研究了SiF2分子的势能曲线，韩晓琴[8]使用从头算的方法优化了SiF2分子的基态结构.但关于SiF2分子在外电场中激发态性质的研究还未见报道.在外电场的作用下，分子内的电子通过从外界吸收一定的能量，由较低能量的基态跃迁至较高能量的激发态，从而对其物理和化学性质产生了很大影响.

为了进一步探讨SiF2分子的激发态性质，本文使用和文献[7]相同的基组对SiF2分子进行研究.尽管文献[7]和文献[8]相比，文献[8]使用QCISD方法更能准确的描述SiF2分子的基态性质，但并不适合描述其激发态行为.因此，本文采用和文献[7]相同的方法进行下面一系列的计算，从而定性的描述SiF2分子激发态的性质，包括激发态能量、激发波长和振子频率等.进一步，为了更准确的描述SiF2分子基态和激发态的特性，本文沿y和z两个方向轴施加不同强度的外电场.首先采用密度泛函理论(DFT)B3P86/6-311++g**(3df,3pd)研究了外电场对SiF2分子基态几何结构、总能量、偶极矩、Mulliken电荷布局、前线轨道等参数的影响.在此基础上，采用杂化CIS/6-311++g**(3df, 3pd)方法计算了外电场下SiF2分子前9个激发态的激发能、吸收峰和振子强度.

1 理论和计算方法

在外电场作用下，分子体系的哈密顿量H[9-11]为

H=H0+Hint

(1)

式中:H0为没有电场存在时的哈密顿量;Hint为电场与分子体系的相互作用能，也就是微扰项.在偶极矩近似下，分子体系与外电场F相互作用哈密顿表示为

Hint=-μ·F

(2)

式中:μ为分子电偶极矩;F为偶极电场.

根据Grozema等[12-13]提出的模型，激发能Eexc为

(3)

式中:Eexc(0)为无电场下的激发能;Δμ为电偶极矩的变化量;Δα为极化率的变化量，它们的大小由电场强度和电场方向决定.振子强度f1u[14]为

(4)

按照SiF2分子的标准坐标，无电场时，采用B3P86/6-311++g**(3df,3pd)方法进行结构优化，结构如图1所示.进一步考虑不同方向外电场对SiF2分子基态结构和激发态特性的影响，沿分子y轴和z轴方向分别加上-0.05、-0.04、-0.03、-0.02、-0.01、0.01、0.02、0.03、0.04，0.05 a.u.的外电场，对分子基态结构和性质等进行了一系列研究.在优化得到不同方向和大小外电场下SiF2分子基态结构的基础上，采用CIS-B3p86/6-311++g**(3df,3pd)方法对SiF2分子外电场下的激发特性(前9个激发态的激发能、激发波长和振子强度)等进行了计算.

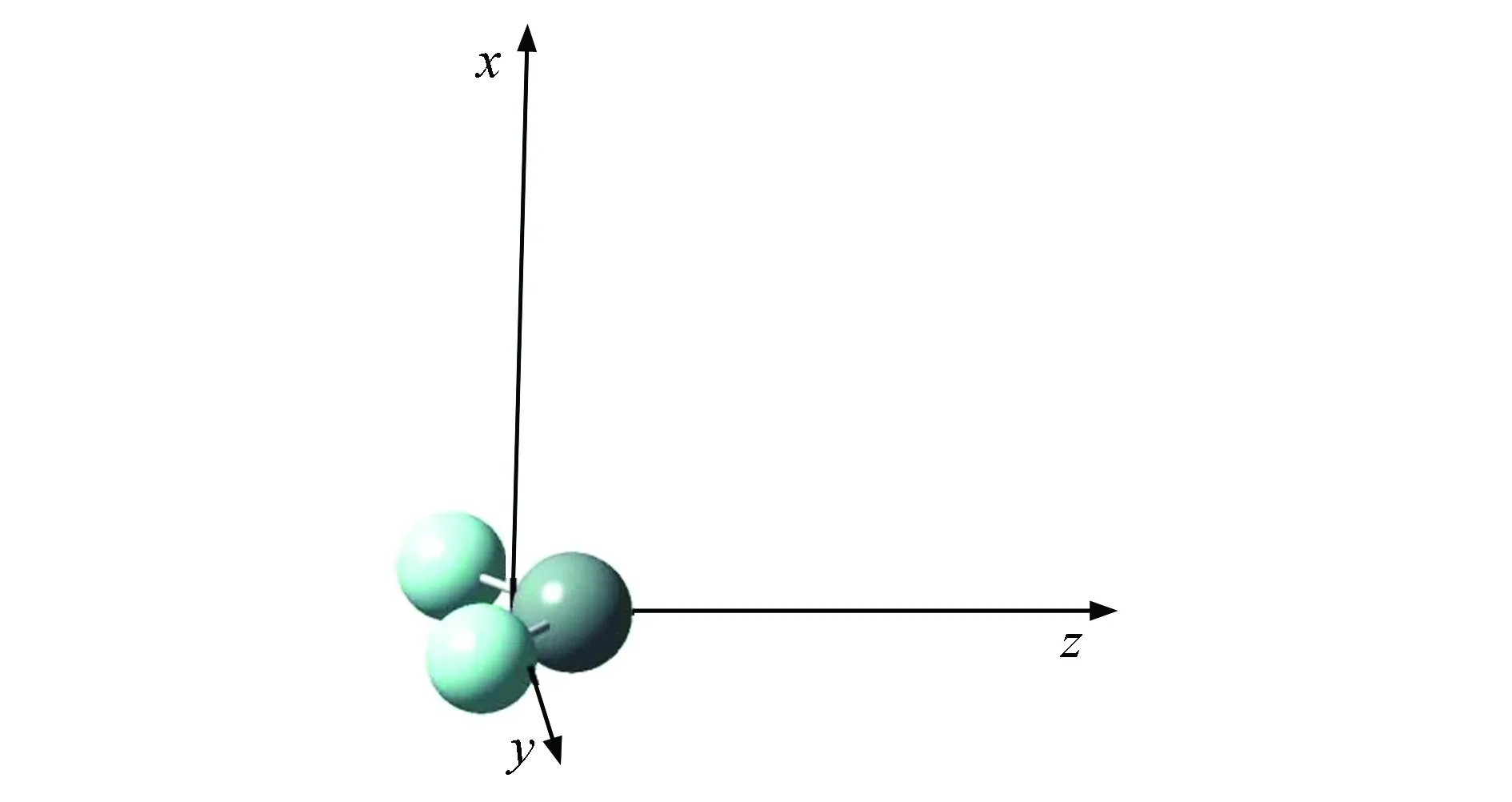
图1 SiF2分子的结构Fig.1 Ground state structure of SiF2 molecule

2 结果与讨论

2.1 外电场对SiF2分子基态构型的影响

使用DFT/B3P86方法在6-311++g**(3df,3pd)基组水平上对SiF2分子结构在y、z轴方向加电场-0.05～0.05 a.u. (1 a.u.=5.142×1011V/m)进行了优化，结果如表1和图2所示.从表1可以看出，在无外电场时，SiF2分子Si—F键长为0.160 84 nm，键角∠F—Si—F为100.679 7°，这与实验值[15]一致.从图2可以看出，沿z轴方向加入外电场后，Si—F键长逐渐减小，从0.171 70 nm变化到0.155 63 nm，减小了0.016 07 nm，而键角∠F—Si—F逐渐增大，两个F原子之间的距离被拉长，在外电场的作用下分子被拉伸，这可以从电荷布局数的改变来进行说明.从表2和图3的电荷布局分布可知，随着外电场的增加，Si原子与F原子之间的库仑吸引力逐渐增强，在外电场力和原子之间作用力的共同影响下，键长逐渐减小.从图2可以看出，从y方向施加电场时，随着外电场的增加，键长从0.160 84 nm增大到0.171 88 nm，增大了0.011 01 nm，而键角∠F—Si—F不断减小，Si原子与F原子之间的库仑吸引力不断减小，从而导致键长的增大.

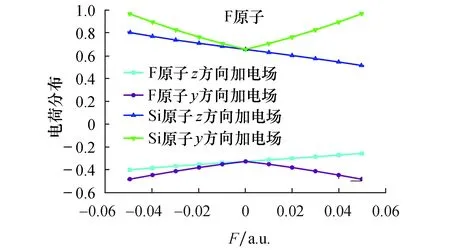
图3 SiF2 分子电荷布局随外电场变化

表1 SiF2分子基态键长、键角和偶极矩随外电场变化

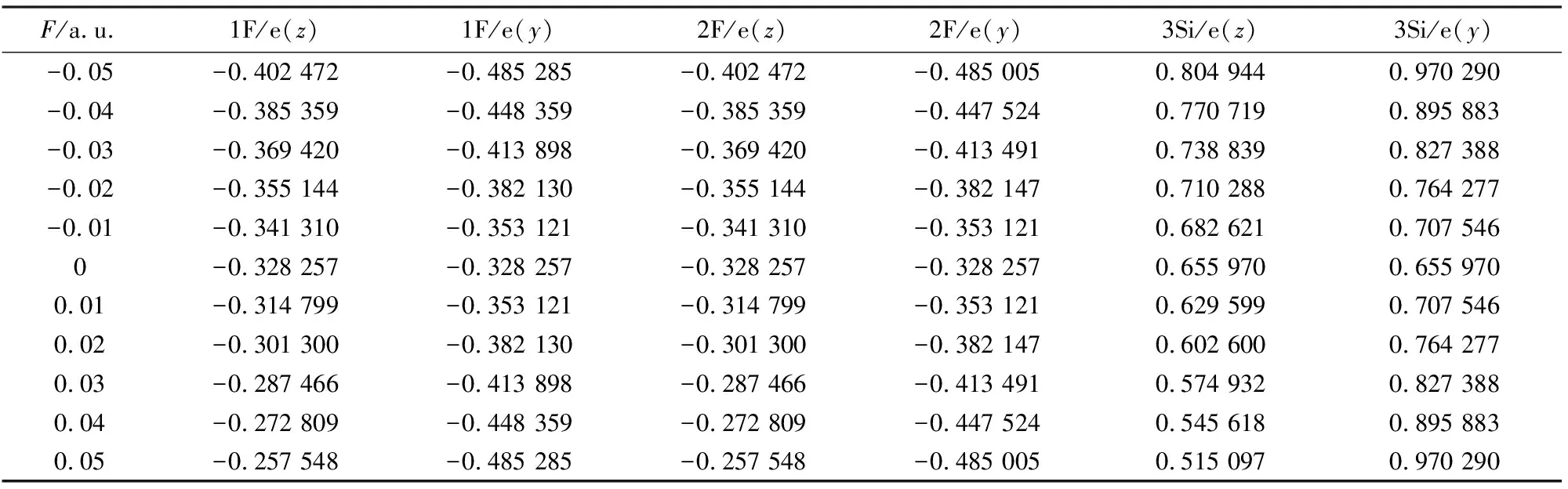
表2 SiF2分子电荷分布随外电场变化

图2 SiF2分子键长、键角随外电场变化Fig.2 Bond length and angle changes of SiF2 molecule with external electric field

2.2 外电场对SiF2分子总能量和偶极矩的影响

体系的总能量E随不同方向外电场F的变化规律如图4所示，随着z方向反向电场的增大，体系能量呈减小的趋势；随着正向电场的增大，体系能量呈上升的趋势，在无电场存在时，体系总能量达到最小值-13 334.412 2 eV.而随着y方向电场的增大，能量呈先增大后减小的变化趋势.能量变化幅度也增大，在无电场时，能量值达到最大.体系总能量在外电场作用下的变化与微扰分子体系和外电场之间的相互作用能(式(2))有关，还与在外电场作用下分子体系内建电场的变化有关.

图4 SiF2分子总能随外电场变化

SiF2分子偶极矩随电场的变化规律在图5给出.随着z方向电场的增大，偶极矩不断减少，这说明在电场的作用下，Si—F原子正负电荷中心的距离越来越近.而随着y方向电场的增大，偶极矩呈先减小后增大的变化趋势.

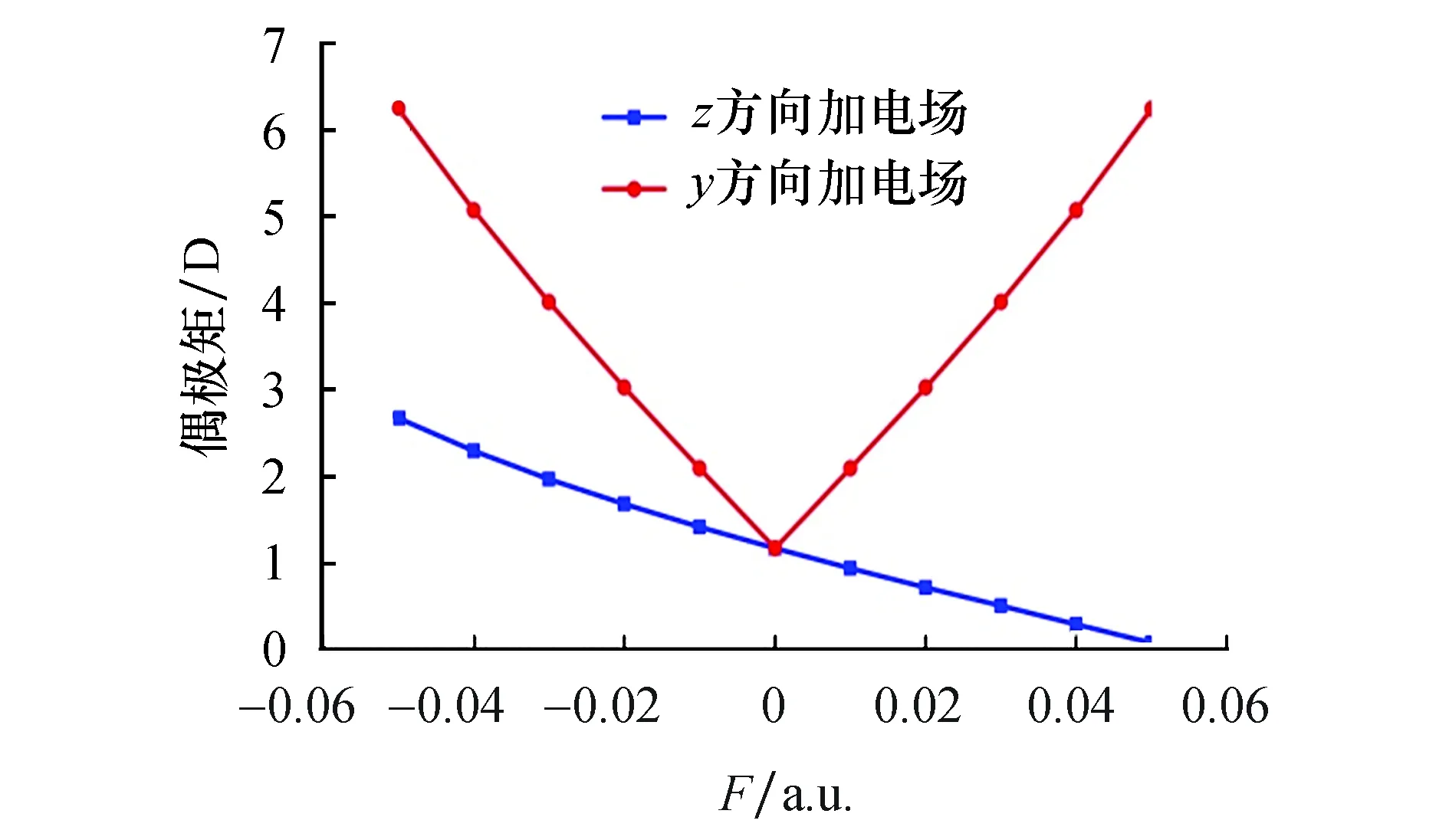
图5 SiF2分子偶极矩随外电场变化 Fig.5 Dipole moment varies of SiF2 molecule with external electric field

2.3 外电场对SiF2分子前线轨道能级、能隙的影响

分子前线轨道包括最高已占据轨道HOMO能级EH和最低未占据轨道LUMO能级EL的数值.EH能级越高，反映分子越容易失去电子，而EL能级越高，反映分子获得电子的能力越强.通过公式Eg=EL-EH，可以求解得到能隙Eg的数值，该值能够反映电子从能级EH向能级EL跃迁的难易程度，并能定性反映分子参与化学反应的能力.从表3可以看出，无电场时，SiF2分子的能隙Eg数值为5.795 8 eV.如图6所示，随着z方向电场的增加，EH和EL均增大，但EH增大的幅度比EL更大，从而使能隙Eg不断减少.能隙Eg的减少说明，外电场的增加使HOMO轨道的电子跃迁至LUMO轨道所需要的能量不断减少，电子越来越容易从HOMO轨道激发至LUMO轨道.而y方向电场的不断增加，使能隙Eg呈先减小后增加的变化趋势.

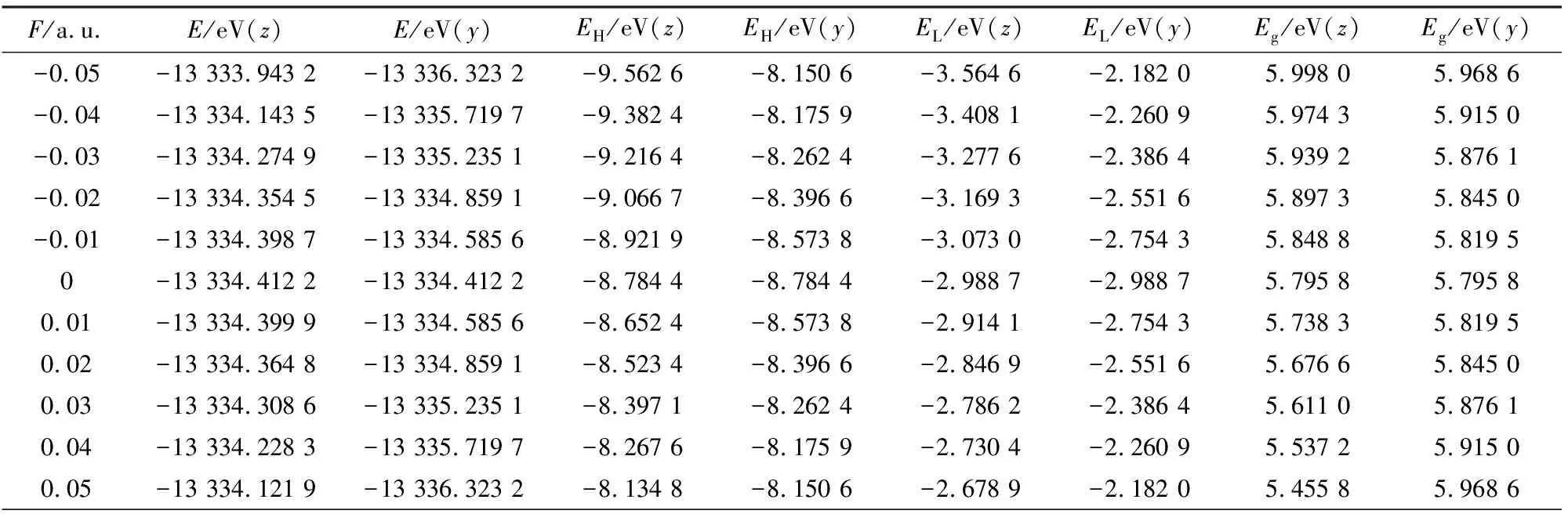
表3 SiF2分子的总能量、HOMO能级EH、LUMO能级EL和能隙Eg随外电场变化

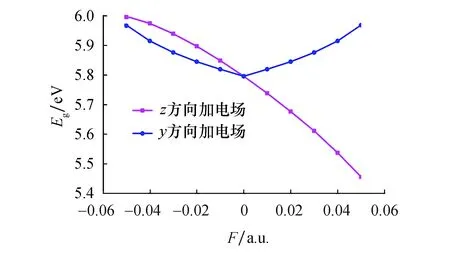
图6 SiF2分子能隙随外电场变化

2.4 外电场对SiF2分子激发态的影响

为了更好的研究不同方向的外电场对SiF2分子性质的影响，在前面优化得到SiF2分子基态结构的基础上，采用杂化CIS方法在B3p86/6-311++g**(3df,3pd)基组上研究了在y和z方向的外电场(-0.05～0.05 a.u.)下SiF2分子的UV-Vis光谱、前9个激发态的激发能、激发波长和振子强度随外电场的变化.计算结果如图7、图8和表4～表9所示.由图7和图8可以看出，没有加电场时，SiF2分子在140.08 nm处出现一个强度较小的吸收峰，吸收强度为3 748.62 L·mol-1·cm-1，而在162.08 nm处出现一个强度较大的紫外吸收峰，吸收强度达到了18 965.50 L·mol-1·cm-1.随着外电场方向的变化和电场强度的不断增强，SiF2分子的紫外吸收峰出现了不同程度的红移或蓝移，但吸收峰都处在紫外区.

表9 SiF2分子的的激发振子强度随外电场(y)变化

图7 SiF2分子的紫外-可见吸收光谱沿z轴方向随外电场变化

图8 SiF2分子的紫外-可见吸收光谱沿y轴方向随外电场变化Fig.8 UV-Vis absorption spectra of SiF2 molecule changes with external electric field along the y-axis

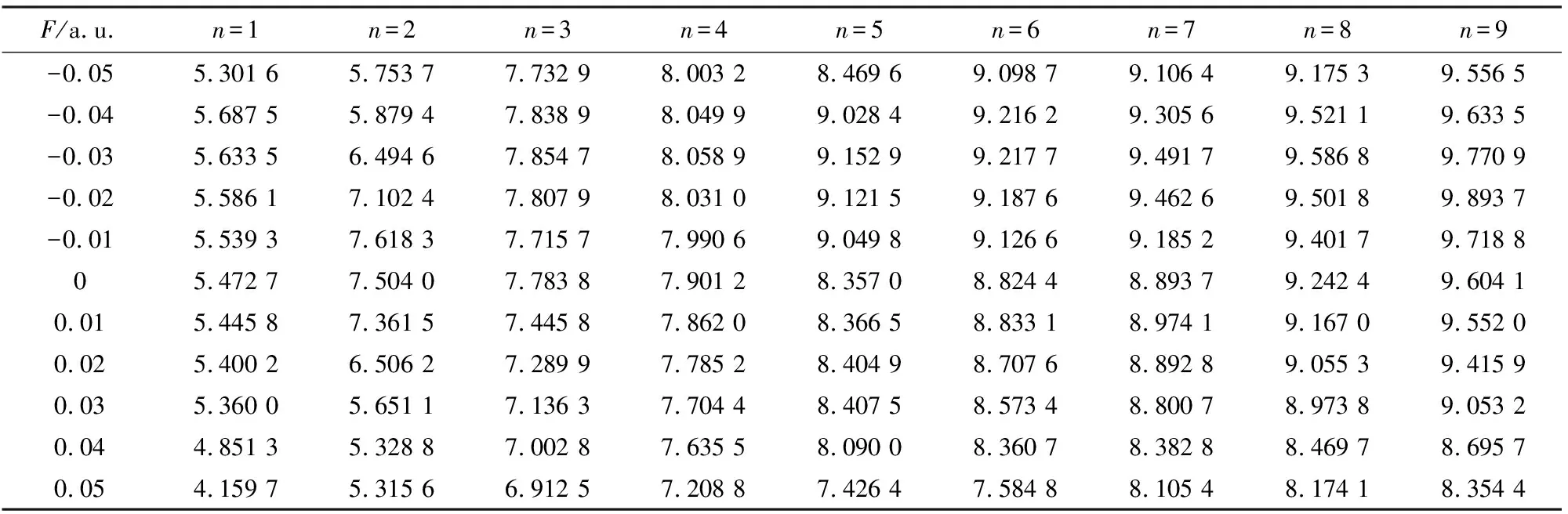
表4 SiF2分子的的激发能随外电场(z)变化

从表4可以看出，随着z方向电场从-0.05增加到0.05 a.u.，SiF2分子前9个激发态的激发能几乎都呈先增加后减小的变化趋势，这说明随着外场增加，SiF2分子更容易激发，这与分子轨道能隙随外电场变化的情况一致，分子轨道的能隙随外电场的不断增加而变小，从而使基态的电子更容易激发.第9激发态在F=-0.02 a.u.时激发能最大，为9.893 7 eV，而第1激发态在F=0.05 a.u.时激发能最小，为4.159 7 eV.从表6可以看出，SiF2分子整个光谱的波长范围在125.32～298.06 nm，属于紫外光谱的范围.随着z方向电场的增加，对应激发波长几乎也呈先增加后减小的变化趋势.在F=-0.02 a.u.时的第9激发态的激发波长最短，为125.32 nm，在F=0.05 a.u.时的第1激发态，激发波长最长，为298.06 nm.从激发能大小的角度进行分析，第1，2激发态的激发能比其他激发态的能量小很多，这说明第1，2激发态的激发相对容易.激发能的变化可以从分子轨道能级的升降和外电场对电子跃迁的影响来进行解释.见表5和表7，随着y方向电场的增加，SiF2分子前9个激发态的激发能并没有发生明显的变化，相应的激发波长都位于紫外光区，也并无明显的变化规律可循.而最大激发能也出现在F=-0.02 a.u.时的第9激发态，激发能为9.966 6 eV，最小激发能出现在F=0.05 a.u.时的第1激发态，激发能为4.264 6 eV.虽然不同方向的外电场对SiF2分子的激发能和激发波长都产生了明显的变化，但都并未出现激发能量简并的现象.这可以从式(3)进行解释.从式(3)可以看出，外电场下的激发能不仅与电偶极矩的变化有关，而且与极化率的变化有关.由于Si和F原子的电负性差别很大，在不同强度和不同方向的电场作用下，电偶极矩和极化率受到不同程度的影响，从而对激发能产生的影响不同，但都产生一定的影响，从而没有出现能量兼并的现象.

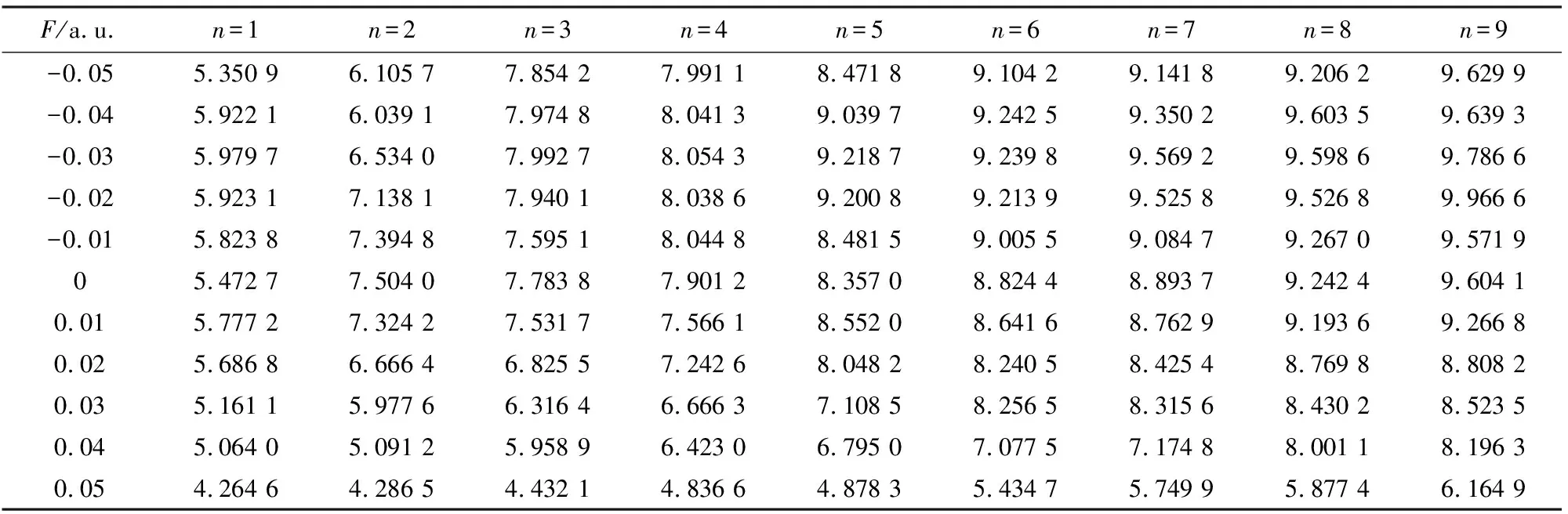
表5 SiF2分子的的激发能随外电场(y)变化

表6 SiF2分子的的激发波长随外电场(z)变化

表7 SiF2分子的激发波长随外电场(y)变化

振子强度的大小反映了电子从基态跃迁到激发态的几率大小，几率越大，振子强度越大，电子越容易从基态跃迁到激发态.振子强度为0，电子不能从基态跃迁到激发态，属于禁阻跃迁.从表8可以看出，随着z方向电场的增加，SiF2分子第4激发态的振子强度均为0，属于禁阻跃迁.而从表9可以看出，当电场方向变为y方向时，第4激发态在F=-0.01，0.01，0.02，0.03 a.u.时，振子强度都不为0.而原有振子强度不为0的激发态，受电场方向影响而变为0，属于禁阻跃迁.例如，在z方向加电场时，第2激发态在F=0.01和0.02 a.u.时振子强度都不为0(表8)，而当电场方向变为y方向时，在F=0.01和0.02 a.u.时，振子强度变为0(表9)，属于禁阻跃迁.

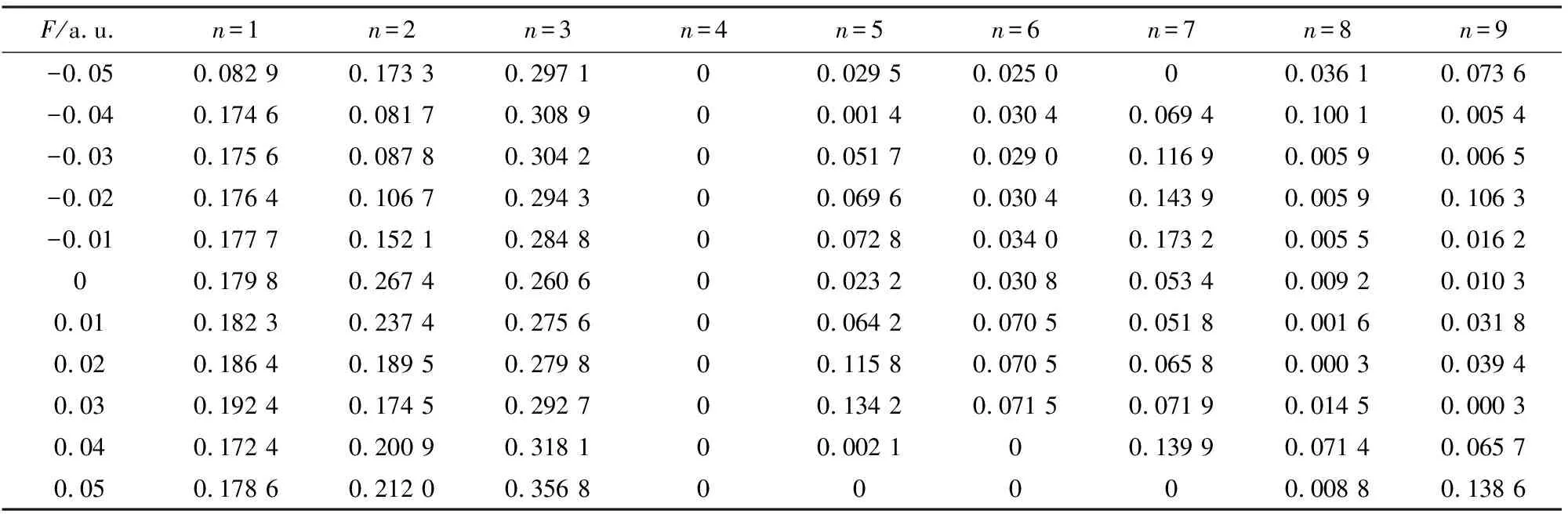
表8 SiF2分子的的激发振子强度随外电场(z)变化

3 结论

本文采用DFT-B3p86/6-311++g**(3df,3pd)方法优化了SiF2分子的基态结构，计算出在y和z轴方向上不同强度外电场下的几何结构、能量、偶极矩、前线轨道能级的影响，在此基础上，采用CIS/6-311++g**(3df,3pd)方法计算了分子的UV-Vis光谱，前9个激发态的激发能、激发波长和振子强度.得出如下结论：

1) SiF2分子的键长、键角、总能量、电荷布局和偶极矩与外电场的大小和方向均有较强的依赖关系.随着z轴方向电场强度由-0.05变化至0.05 a.u.，键长不断减小，总能量先减小后增大，偶极矩不断减小，而当y轴电场方向不断增大时，键长先减小后增大，总能量先增大后减小，偶极矩先减小后增大，电荷分布受两种电场方向的影响比较明显，但并没有改变原子的电性.

2) SiF2分子的HOMO能级和LUMO能级受外电场的影响明显，能隙在外电场的作用下变化显著，这影响了SiF2分子参与化学反应的能力.

3) 在y轴和z轴两种方向的外电场下，激发能和激发波长的变化较为复杂.振子强度不但可以通过电场强度的大小改变，也可以通过外电场的方向进行改变.

致谢：本文得到凯里学院博士专项课题(BS 201601,BS201702)的资助，在此表示感谢.