组合结构波纹管膜片非线性大挠度分析

韩明君, 周朝逾, 李鸿瑞, 马连生

(兰州理工大学 理学院, 甘肃 兰州 730050)

波纹管是应用于密封系统中的一类弹性元件,波纹管管壁比较薄,灵敏度比较高,主要应用于补偿管线热变形、减震、吸收管线沉降变形等作用,在波纹管密封系统领域的研究中,国内外学者对此做出了很大的突破[1-5].对波纹管应力及变形等方面的研究采用的方法很多,Aleksander等[6]把在轴对称载荷作用下波纹管认为是波纹的旋转壳，研究了U形膨胀波纹管在内压载荷作用下的应力应变状态.丁雪兴等[7]利用 ANSYS程序对机械密封焊接金属波纹管波纹膜片进行动态响应分析,求出了固有频率和振型,为波纹管的动态响应分析提供了依据.黄乃宁等[8]用应变寿命法对金属波纹管的寿命进行了研究，并且得出不同材料的性能对金属波纹管的寿命造成不同程度的影响，比较准确的分析出金属波纹管的疲劳寿命，有效地提高了波纹管的使用水准.Faraji等[9]利用商业软件(ABAQUS/EXPLICIT)对金属波纹管进行有限元模拟,以找出最佳设计参数.使用估计的设计参数得出可接受的产品.在实验分析中得出产品的质量与回弹量、冠径和厚度分布关系.Marcal等[10]采用NON-LIN 程序,考虑了弹塑性和大位移,以波纹管承载后的变形测量为基础,评定U型和焊接膜片波纹管.樊大钧等[11]用无量纲变尺度优化的数值积分初参数方法和自编程序,对焊接圆弧波纹管的线性和非线性特性进行了分析.

以上文献都是用有限元数值模拟的方法分析了工程中的一些问题,但是由于波纹管结构的复杂性,这些方法缺乏解析法所具有的通用性.对波纹管结构模型用解析法研究的较少[12],最早是依赖于简单的梁模型近似法,Freely等[13]通过将锥形壳体近似简化为平板,采用梁理论对焊接膜片波纹管的应力进行了分析.Dinno等[14]提出了一种计算轴对称载荷作用下厚壳回转体下限极限压力的方法.通过该方法求出了有限几何参数范围内的结果.王新志等[15]根据薄壳非线性动力学理论,用修正迭代法求解出二次近似解析解,把大挠度解作为扁球薄壳的初挠度处理,推导出了扁球薄壳在大挠度下的非线性动力学基本方程.

由于运用解析法对波纹管膜片求解的难度比较大,本文通过连续化方法建立组合结构波纹管膜片的精确力学模型,将其简化为具有初挠度的圆环薄板,通过薄壳的非线性大挠度理论[16],求解了扁圆锥壳-圆弧-圆环板组合结构波纹管膜片的无量纲控制方程,利用迭代原理,根据边界条件和连续条件,得到了精确度较高的二次解析解,讨论了扁圆锥壳-圆弧-圆环板组合结构波纹管膜片的不同倾斜角斜边波形、圆弧部分不同矢高以及圆弧部分不同波长在膜片最大变形处的挠度和载荷的关系,波纹管的微小变形将直接影响密封气膜流场,从而对密封性能产生影响,优化波纹管可以提高密封性能.此分析结果对干气密封系统中波纹管的结构优化设计有一定的参考价值,可以在工程中根据实际的需要选取合适的波纹管.

1 基本方程和边界条件

将组合结构波纹管膜片看作是具有初挠度的圆环板结构,根据连续化方法对膜片进行非线性大变形分析,扁圆锥壳-圆弧-圆环板组合结构波纹管膜片是一个呈轴对称结构的圆环薄壳,膜片的立体视图如图1所示,由于膜片倾斜角的角度不同,从而使其波形结构也不同.膜片不同倾斜角斜边波形如图2所示,取45°斜边波形膜片模型简化图如图3所示.具有初挠度组合结构波纹管膜片的厚度为t,膜片的内外半径分别为d、a,组合结构波纹管膜片中圆弧波长为2R,矢高为h,扁圆锥壳部分膜片的矢高为f,膜片的外边界固定,内边界自由.膜片受到均布载荷q和集中力P的作用,对如图4所示的膜片进行非线性大变形计算分析.由于波纹管结构为膜片内位焊接而成,故其变形可以简化为一端固定一端自由.将组合结构波纹管膜片看作是具有初挠度的圆环薄板,建立坐标系：r为径向坐标,w为挠度,Nr为径向薄膜力.

图2 波纹管膜片波形图Fig.2 Bellows diaphragm waveform

图3 波纹管膜片模型简化图Fig.3 Simplified diagram diaphragm’s model

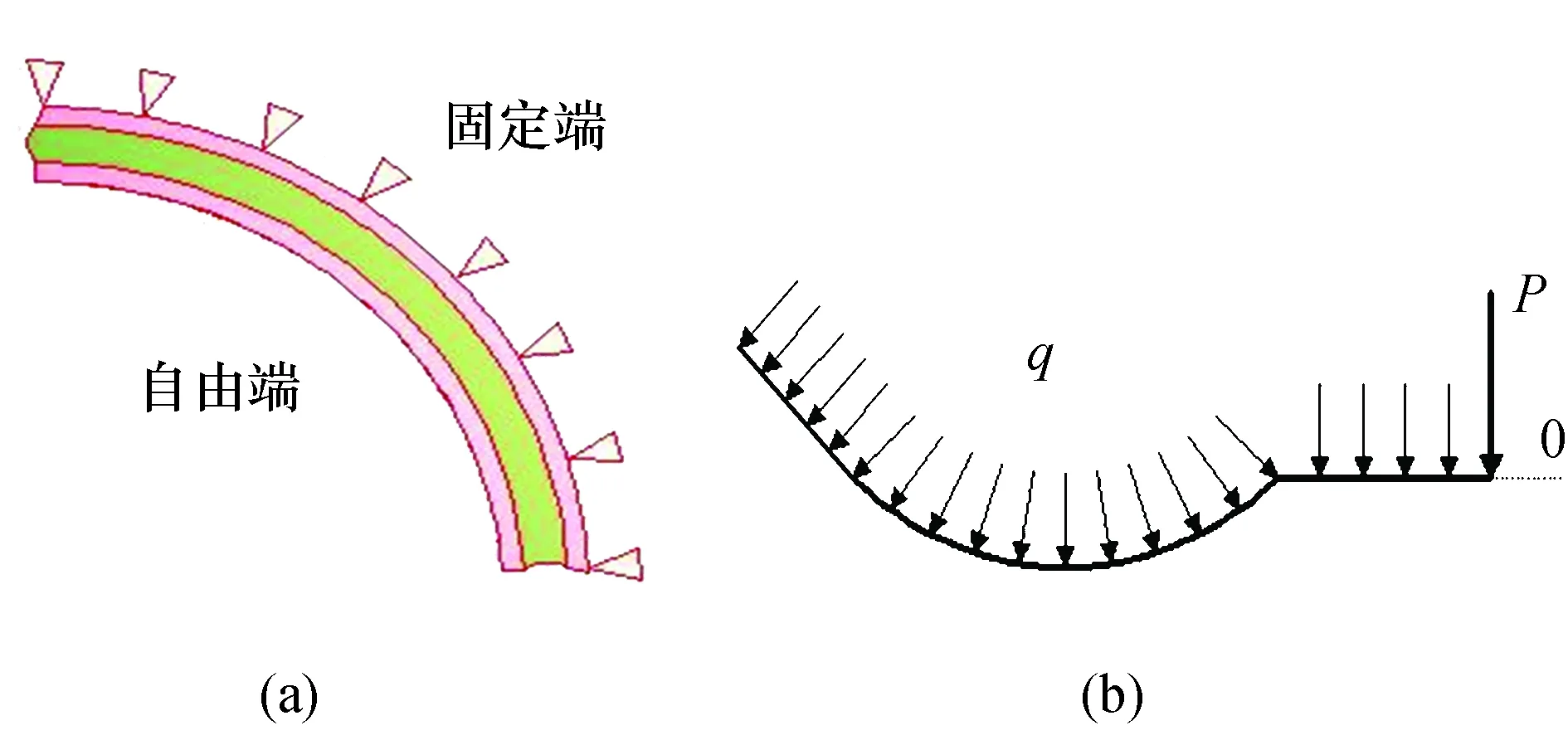
图4 膜片力学模型

通常将扁圆锥壳-圆弧-圆环板组合结构波纹管膜片中的扁锥壳部分和圆弧部分认为是圆环薄板所具有的初挠度,取

(1)

式中:wa为组合结构波纹管膜片在扁锥壳部分的初挠度;wb为组合结构波纹管膜片在圆弧部分的初挠度.

组合结构波纹管膜片的基本方程组如下[17-18]：

扁圆锥壳部分满足如下方程组:

(2)

圆弧膜片部分的基本方程组：

(3)

圆环板部分的基本方程组：

(4)

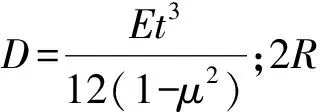
周边固定处边界条件为

(5)

自由周边处边界条件为

(6)

连续处边界条件为

式中

(·)(1)表示组合结构波纹管膜片具有初挠度扁圆锥壳部分；

(·)(2)表示组合结构波纹管膜片具有初始挠度的圆弧部分；

(·)(3)表示组合结构波纹管膜片内部无初挠度圆环薄板部分.

为了计算方便,引入下列无量纲量:

引入三个阶梯函数ρ1、ρ2、ρ3后,将方程(2～4)可简洁的进行合并,将引入的无量纲量代入所合并的方程组,便可得到无量纲控制方程,具体表示如下：

(9)

此即无量纲化后的控制方程.方程中的3个阶梯函数为

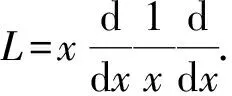
由无量纲表示的边界条件如下:

固定周边处

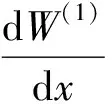
(10)

自由周边处

(11)

连续处

2 对基本方程求解

组合结构波纹管膜片的扁圆锥壳部分位于膜片固定端；而膜片的圆弧部分则位于膜片中间部分,将膜片的扁圆锥壳部分和圆弧部分看作是由具有初挠度的圆环薄板,波纹管膜片由扁圆锥壳、圆弧、圆环板三部分组合而成.利用修正迭代法对膜片的挠度W进行二次近似求解,可以得到组合结构波纹管膜片的非线性解析值.

2.1 具有初挠度扁圆锥壳部分膜片的基本方程求解

当b/a≤x≤1时,扁圆锥壳部分膜片的基本方程为

(14)

利用修正迭代法对基本方程(14)进行求解.

对于一次近似,有

(15)

(16)

(17)

式中

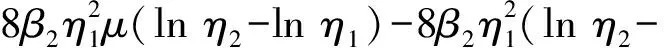
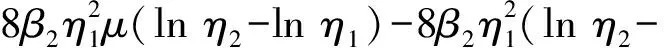
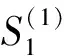
对于二次近似,有

(18)

2.2 具有初始挠度的圆弧部分的基本方程求解

当c/a≤x≤b/a时,圆弧部分膜片的基本方程为

(19)

利用修正迭代法对基本方程(19)进行求解.对于一次近似,有

(20)

对于二次近似,有

(23)

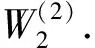
2.3 内部无初挠度圆环薄板部分的基本方程求解

当d/a≤x≤c/a时,圆环薄板膜片的基本方程为

(24)

利用修正迭代法对基本方程(24)进行求解.对于一次近似,有

(25)

式中

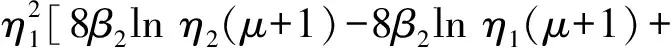
对于二次近似,有

(28)

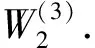
3 数值计算和结果分析

选取合适的组合结构波纹管膜片的材料,组合结构波纹管膜片的外径确定为a=80 mm,内径确定为d=65 mm,圆弧部分膜片的波长为2R,波纹管膜片的弹性模量E=187 GPa,泊松比μ=0.3,膜片的壁厚为t=0.15 mm.将这些参数代入到上式各级表达式中,通过对应关系求得各个表达式的积分常数,取波纹管膜片在最大变形处的挠度为W0,得出结果如下：

通过对方程组的二次近似求解可得到扁圆锥壳-圆弧-圆环板组合结构波纹管膜片的挠度与载荷的非线性关系,因此当组合结构波纹管膜片的波长、矢高都为设定值,波纹管膜片在最大变形处发生大挠度变形时,膜片不同倾斜角的斜边的波形在圆弧最大挠度处的载荷和挠度呈现非线性关系,不同倾斜角的斜边波纹管膜片最大变形处挠度W0和载荷Q2的非线性特征曲线如图5所示.

图5 波纹管膜片在不同倾斜角波片下的大挠度平衡路径Fig.5 Large deflection balance path of bellows diaphragm under different inclination angles diaphragm

由图5可以看出组合结构波纹管膜片在不同倾斜角波片下膜片最大变形处挠度的非线性特征关系,反映了不同载荷和不同倾斜角的波片作用下膜片的弯曲情况.图5a表示在均布载荷(β1=1,β2=0)作用下、圆弧部分的波长为定值(2R=4 mm)以及圆弧的矢高固定(h=0.5 mm)时,波纹管膜片的倾斜角分别取γ=0°、30°、45°、60°时挠度与载荷的非线性关系；图5b表示在集中力(β1=0,β2=1)作用下、圆弧部分的波长为定值(2R=4 mm)以及圆弧的矢高固定(h=0.5 mm)时,波纹管膜片的倾斜角分别取γ=0°、30°、45°、60°时挠度与载荷的非线性关系.图5c表示在复合载荷(β1=1,β2=1)作用下、圆弧部分的波长为定值(2R=4 mm)以及圆弧的矢高固定(h=0.5 mm)时,波纹管膜片的倾斜角分别取γ=0°、30°、45°、60°时挠度与载荷的非线性关系.通过特征关系可知,当膜片无倾斜角(γ=0°)时,膜片受到载荷时最容易发生变形,随着波纹管膜片倾斜角的增大(γ=30°,γ=45°,γ=60°),波纹管膜片的承载能力越强,随着圆弧挠度的增加,膜片发生变形时所需要的载荷呈现的非线性增加.

当波纹管膜片倾斜角的斜边波形固定不变时,圆弧部分不同矢高的波纹管膜片在圆弧最大挠度处的载荷和挠度呈现非线性关系,其波纹管膜片最大变形处挠度W0和载荷Q2的非线性特征曲线如图6所示.

图6 波纹管膜片在矢高变化下膜片的大挠度平衡路径Fig.6 Large deflection balance path of bellows diaphragm under variation of vector height

图6反映出当组合结构波纹管膜片倾斜角固定(γ=45°)以及圆弧部分膜片波长(2R=4)固定不变的情况下,不同载荷在不同矢高作用下膜片的挠度变化情况.图6a表示在均布载荷作用下(β1=1,β2=0)、圆弧部分的波长为定值(2R=4 mm)以及膜片倾斜角(γ=45°)固定时,组合结构波纹管膜片圆弧部分的矢高分别取h=0、0.25、0.5、0.75 mm时挠度与载荷的非线性关系；图6b表示在集中力作用下(β1=0,β2=1)、圆弧部分的波长为定值(2R=4 mm)以及膜片倾斜角(γ=45°)固定时,组合结构波纹管膜片圆弧部分的矢高分别取h=0、0.25、0.5、0.75 mm时挠度与载荷的非线性关系；图6c表示在复合载荷作用下(β1=1,β2=1)，圆弧部分的波长为定值(2R=4 mm)以及固定端膜片倾斜角(γ=45°)固定时,组合结构波纹管膜片圆弧部分的矢高分别取h=0、0.25、0.5、0.75 mm时挠度与载荷的非线性关系.通过特征关系可知,当膜片圆弧部分的矢高为h=0 mm时(即圆弧部分变为圆环板时),膜片受到载荷时越容易发生变形；随着波纹管膜片圆弧矢高的增加(h=0.25、0.5、0.75 mm),膜片受到载荷作用时使膜片发生的变形达到平衡路径越容易,膜片的承载能越强；随着圆弧挠度的增加,膜片发生变形所需要的载荷呈现的非线性增加.

当波纹管膜片倾斜角的斜边的波形和圆弧部分矢高固定时,圆弧部分不同波长的膜片在圆弧最大挠度处的载荷和挠度呈现非线性关系,其纹管膜片最大变形处挠度W0和载荷Q2的非线性特征曲线如图7所示.

图7反映了圆弧部分不同波长的膜片在圆弧最大挠度处不同载荷作用下载荷和挠度呈现非线性弯曲情况.图7a表示在均布载荷作用下(β1=1,β2=0)圆弧部分的矢高为定值(h=0.75 mm)以及固定端膜片扁锥壳部分的倾斜角(γ=45°)固定时,组合结构波纹管膜片圆弧部分的波长分别取2R=4、5、6 mm时挠度与载荷的非线性关系；图7b表示在集中力作用下(β1=0,β2=1)圆弧部分的矢高为定值(h=0.75 mm)以及固定端膜片扁锥壳部分的倾斜角(γ=45°)固定时,组合结构波纹管膜片圆弧部分的波长分别取2R=4、5、6 mm时挠度与载荷的非线性关系；图7c表示在集中力作用下(β1=1,β2=1)，圆弧部分的矢高为定值(h=0.75 mm)以及固定端膜片扁锥壳部分的倾斜角(γ=45°)固定时,组合结构波纹管膜片圆弧部分的波长分别取2R=4、5、6 mm时挠度与载荷的非线性关系；通过特征关系可知,随着波纹管膜片圆弧波长的增加(2R=4、5、6 mm),膜片受到载荷作用时使膜片发生的变形达到平衡路径也越容易,膜片的承载能力也随之越强；随着圆弧挠度的增加,膜片发生变形所需要的载荷呈现的非线性增加.

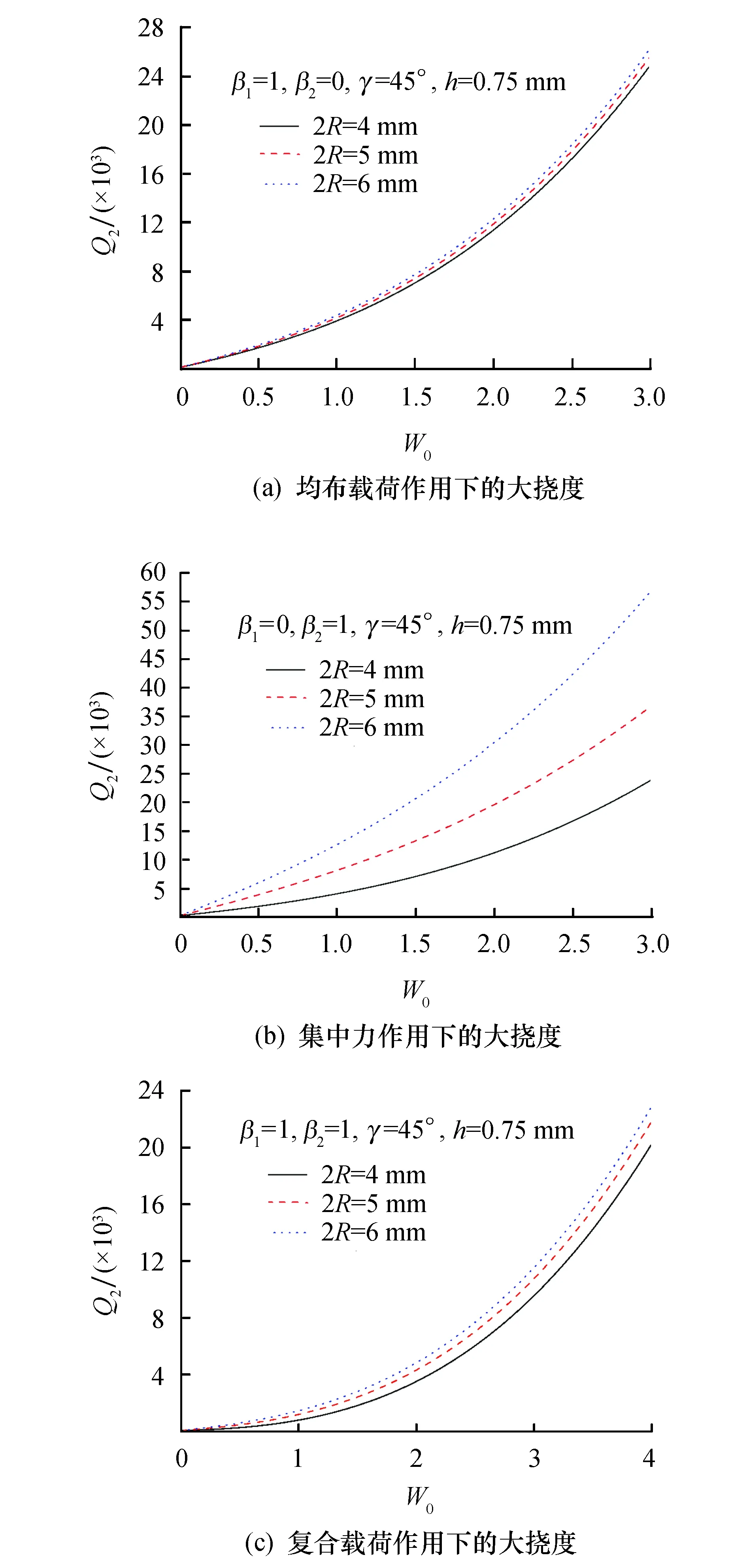
图7 波纹管膜片圆弧部分波长变化下膜片的大挠度平衡路径

4 结论

1) 扁圆锥壳-圆弧-圆环板组合结构波纹管膜片具有类似于均匀材料圆环薄板的载荷与挠度的关系,在等效连续化方法的基础上,将扁圆锥壳-圆弧-圆环板组合结构波纹管膜片膜片看作是连续的圆环薄板,采用修正迭代法求解了波纹管膜片的非线性大变形问题.为波纹管结构的优化提供了重要依据.

2) 随着载荷的增大,扁圆锥壳-圆弧-圆环板组合结构波纹管膜片的挠度也逐渐增大,同时,波纹管膜片扁锥壳部分的膜片的倾斜角对其变形有很大的影响；随着膜片倾斜角的增大,最大变形处的挠度也相应增大,膜片的挠度非线性增大.同样可以得出,随着波纹管膜片圆弧部分的矢高的增加,膜片的挠度非线性增大,随着波纹管膜片的弧长变长,膜片的挠度非线性增大.波纹管膜片中圆弧部分的矢高越大,膜片的承载能力就会越强；圆弧部分波长越长,膜片的承载能力就会越强.

3) 扁圆锥壳-圆弧-圆环板组合结构波纹管膜片发生的变形不仅与膜片本身具有的性质有关,而且与膜片的结构形状也有关,扁圆锥壳部分的尺寸比例也起着比较关键的作用,合理的选择波纹管膜片的波形及其矢高和波长,可以优化波纹管的使用价值,使干气密封的效果达到最佳.