大跨度铁路桥梁梁端伸缩装置性能研究
杨静静 高芒芒 蒙蛟 柯在田
1.中国铁道科学研究院集团有限公司基础设施检测研究所,北京100081;2.中国铁路设计集团有限公司,天津300251
大跨度铁路桥梁在梁端设置伸缩构造(梁端伸缩装置与钢轨调节器)用于保证钢轨在主桥、引桥梁缝处的可靠过渡和支承,同时适应温度、风、列车活载等作用下的主桥、引桥梁端变位。梁端伸缩装置作为大跨度铁路桥梁梁端部位的特殊构造,除需要适应梁端位移和转角等空间变位,也应具有足够的强度与合理的刚度,以保证高速列车的安全性和平稳性[1-3]。
大跨度铁路桥梁具有不同的约束体系,由温度、风、列车等引起的梁端变位特征各不相同。梁端伸缩装置一般需要专门设计,并通过开展车-桥-伸缩装置耦合振动分析验证其综合性能[4-6]。
虽然直接耦合动力分析可以计入梁端伸缩装置振动对车辆性能的影响,但由于梁端伸缩装置的有效计算范围很短,随机不平顺的影响相对较大,计算结果难以反映最不利情况。车桥耦合振动分析可以对梁端伸缩装置的性能起到验证的作用。
梁端伸缩装置长度远小于主桥和引桥,变形主要表现为中短波不平顺,对行车安全性产生影响。为对梁端伸缩装置的性能进行评估,以某1 500 m级超大跨度斜拉-悬吊协作体系公铁两用大桥为例,拟从两个方面开展工作:①梁端伸缩装置的轨道平顺状态采用10 m弦测值进行评定。消除随机不平顺的影响后,可参考TG/GW 115—2012《高速铁路无砟轨道线路维修规则》[7]得到梁端伸缩装置范围内轨面变形的10 m弦控制建议值。②开展车-桥-伸缩装置耦合振动分析,对脱轨系数、轮重减载率、车体加速度等车辆动力响应进行评判。
1 工程概况
某公铁两用大桥为主跨1 488 m的斜拉-悬吊协作体系桥,孔跨布置为(70+112+406+1 488+406+112+70)m。该桥结构体系采用塔梁分离、塔墩固结形式,塔梁之间设置支座和纵向阻尼器。大桥立面布置见图1。

图1 大桥立面布置(单位:m)
该桥为双线客运专线,速度目标值为250 km/h,正线线间距4.6 m,到发线有效长度650 m。客车采用8节编组的动车组,高速公路为双向六车道,路面总宽33 m,设计速度100 km/h,采用公路Ⅰ级荷载。
采用MIDAS/Civil建立该桥整体有限元模型。索塔和分离式钢箱梁采用梁单元模拟,主缆、吊索和斜拉索采用索单元模拟。斜拉索、塔顶主缆与索塔之间均采用刚性连接模拟,计算时考虑斜拉索和缆索垂度、大位移等的几何非线性。
该桥采用上承式梁端伸缩装置方案(图2),温度伸缩量为±900 mm。中和温度梁缝1 580 mm,设置4根活动钢枕、4根支承纵梁。钢轨内外侧各设置2根支承纵梁,采用工字形截面,尺寸为220 mm×280 mm(高度×宽度)。梁缝区4根活动钢枕同样采用工字梁结构,尺寸为300 mm×200 mm(高度×宽度)。无外力状态下,活动枕间距400 mm,对应最大伸长量为580 mm,最大缩短量为220 mm。
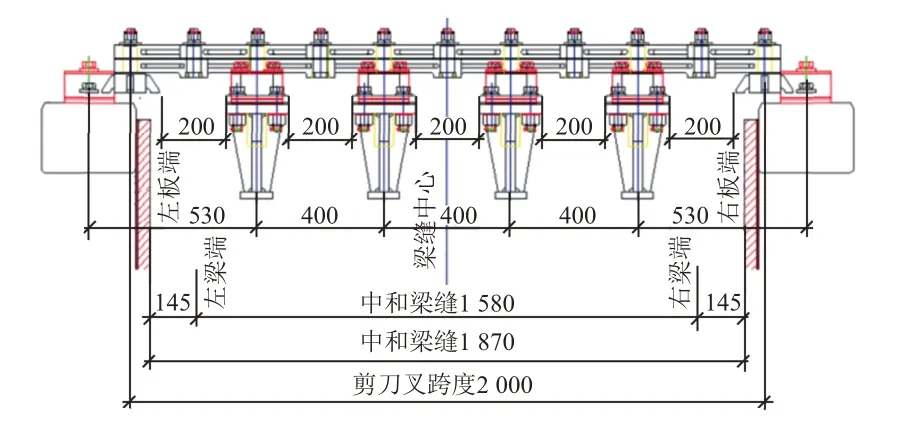
图2 上承式梁端伸缩装置方案布置(单位:mm)
降温状态下最大伸长的梁端伸缩装置模型见图3。
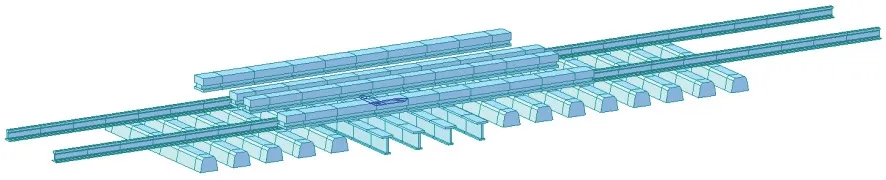
图3 降温状态下梁端伸缩装置模型
2 轨道形位评价的计算工况与分析
对轨道形位的评价采用10 m弦方法,首先应确定路基区段轨道随机不平顺的10 m弦测值。消除随机不平顺的影响后,可参考TG/GW 115—2012得到梁端伸缩装置范围内轨面变形的10 m弦控制建议值。
2.1 路基区段轨道随机不平顺的10 m弦测值
选取某客运专线路基段的不平顺实测数据进行10 m弦分析。高低不平顺和轨向不平顺的10 m弦测值见图4。可见,路基区段轨道随机不平顺对应的10 m弦测值高低不平顺为3 mm,轨向不平顺为2 mm。

图4 某客运专线路基区段轨道高低、轨向不平顺10 m弦测值
2.2 梁端伸缩装置范围内轨面变形的10 m弦控制建议值
梁端伸缩装置附近区域的轨道平顺状态明显受到温度、横风、多线行车等因素的影响,在长期使用状态下还可能出现病害。为保证行车安全,需要分析最不利工况组合条件下的轨道状态。考虑到这些外部环境因素共同作用存在一定概率,本文综合考虑行车和环境因素影响,同时参考TG/GW 115—2012中“表6.2.1线路轨道静态几何尺寸容许偏差管理值”的规定并适当放宽标准,对梁端伸缩装置的性能提出分级管理的原则,对上述环境因素采用不同的荷载组合及10 m弦控制建议值,见表1。
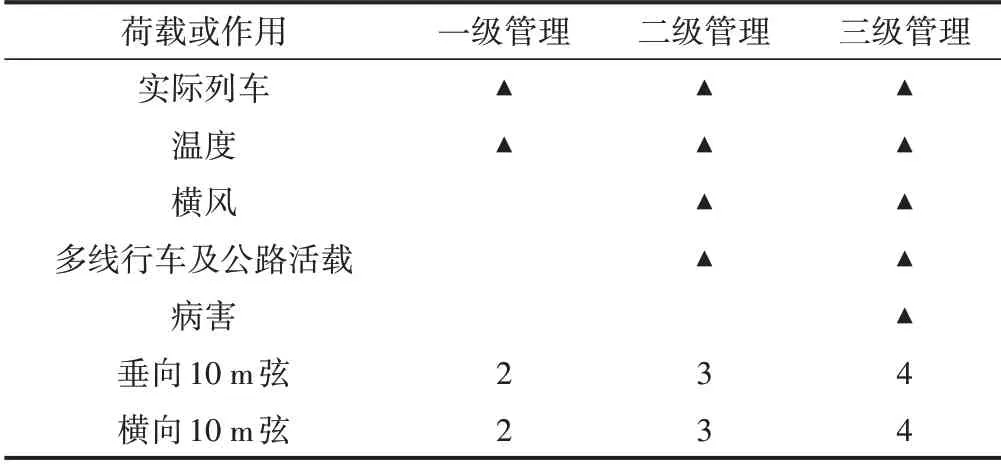
表1 荷载组合及相应桥面变形10 m弦控制建议值
上述管理标准涉及伸缩缝病害,根据前期调研可将病害分为三类:伸缩装置处钢枕出现八字形变形;单根活动钢枕发生偏斜;活动钢枕整体纵向偏移。其中八字形变形出现频率较高,应考虑左右间距差100 mm且相邻活动钢枕同时出现歪斜的不利工况。活动钢枕的位置见图5。
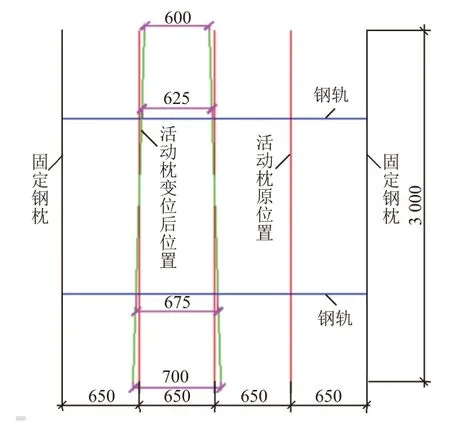
图5 八字形变形轨枕相对位置(单位:mm)
2.3 计算模型及分析
梁端伸缩装置的完整分析模型长度应涵盖主桥的辅助跨和边跨、伸缩装置以及引桥。为简化梁端伸缩装置的分析模型,本文仅在主桥、引桥相应位置建立有砟轨道结构。完整的梁端伸缩装置模型包含钢轨、固定枕、活动枕、支撑梁、主引桥的轨枕质量块。轨下胶垫及道砟用弹簧连接模拟。
模型施加的外荷载有:①将主桥、引桥在列车荷载、公路活载、温度作用下的变形曲线处理为强迫位移,得到从主桥到引桥区段的钢轨初始变形;②列车在通过梁端伸缩装置时的钢轨变形。将①和②叠加即为列车通过梁端伸缩装置时的钢轨实际变形。
根据文献[7]中静态几何尺寸的定义,表1中不同等级管理时各组合工况对应的轨道变形均不考虑动力效应,且均须要对伸缩装置达到最大伸长与最大缩短、梁端折角达到最大正负值的情况分别考虑。某动车组对应的列车荷载,公路活载以及整体升降温作用引起的钢轨初始变形见图6。根据JTG D60—2015《公路桥涵设计通用规范》[8],公路活载=六车道汽车荷载×0.55(横向折减系数)×0.92(纵向折减系数)。

图6 钢轨初始变形
为分析不同工况的影响,分别计算列车荷载、公路活载、整体升降温作用及其组合工况下轨道形位的10 m弦测值,计算结果见表2。

表2 荷载组合及相应的轨道形位10 m弦测值 mm
由表2可知,单独考虑列车荷载、公路活载、整体升降温作用以及活动钢枕的病害时,10 m弦测值最大为1.563 mm,对应整体升温作用;考虑各种荷载的组合时,10 m弦测值最大为2.303 mm,对应组合工况为列车荷载+公路活载+整体升温26℃引起最小梁端折角,满足表1二级管理时10 m弦测值小于3 mm的限值要求。
3 车桥动力耦合的计算工况与分析
车桥动力分析的模型、计算工况与轨道形位分析时相同,仅评价标准变更为车辆动力响应的控制标准。
参考TB 10621—2014《高速铁路设计规范》[9]的相关规定适当放宽,并对梁端伸缩装置的性能提出分级管理的原则,车桥动力分析的荷载组合及车辆动力响应控制建议值见表3。

表3 荷载组合及相应车辆动力响应控制建议值
车桥动力分析同样需要考虑梁端伸缩装置最大伸长、最大缩短两种状态,分析时温度、横风以及公路活载的作用均按附加不平顺处理,主引桥在列车荷载下的变形也处理为附加不平顺,从而能够模拟最不利梁端折角的影响。
3.1 车辆模型
本文采用的列车荷载为8节编组的动车组列车。单节车辆的动力方程为[10-12]
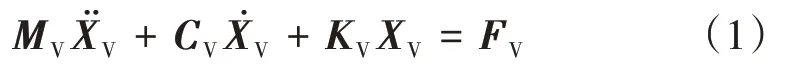
式中:MV,CV,KV分别为单节车辆的单元质量矩阵、单元阻尼矩阵、单元刚度矩阵,由Lagrange方程求得;XV为车辆的位移向量;FV为单节车辆所受的力向量,即轮轨间作用力。
3.2 桥梁模型
桥梁子系统的动力方程[10-12]为

式中:MB,CB,KB分别为桥梁子系统的总体质量矩阵、总体阻尼矩阵、总体刚度矩阵,由有限元法可求出MB,KB,由比例阻尼法可求出CB;XB为桥梁的位移向量;FB为桥梁所受的力向量,即各节车辆对桥梁的作用力之和。
3.3 轮轨间相互作用关系
法向轮轨关系采用Hertz非线性接触理论,切向轮轨关系采用kalker线型理论确定蠕滑力[10-12]。
3.4 计算结果及分析
与10 m弦分析类似,为考察不同工况的影响,分别将整体升降温作用、列车荷载、公路活载及其组合工况下的钢轨初始变形作为附加不平顺进行车桥耦合动力分析,钢轨间距最大时不同荷载下车辆动力响应结果见表4。其中轨道随机不平顺选取图4对应的某客运专线路基段的不平顺实测数据。
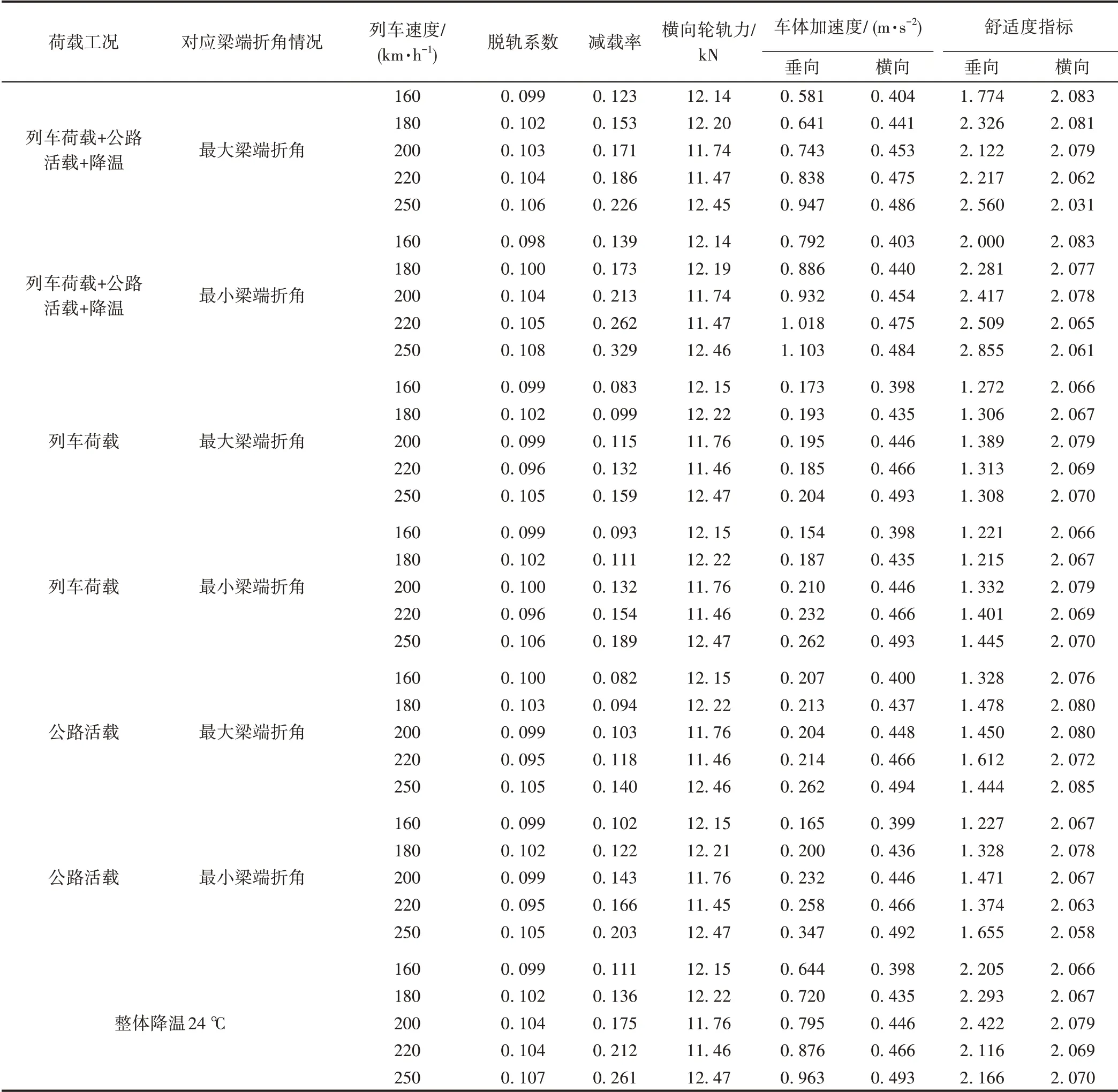
表4 钢轨间距最大时不同荷载下车辆动力响应
由表4可知:整体温度作用、列车荷载、公路活载各因素单独作用下,车辆的动力性能均满足要求,减载率最大为0.261,车体振动加速度最大为0.963 m/s2,均发生在整体温度作用工况,因此所有的独立影响因素中,温度对车辆动力响应的影响最大;在组合荷载作用下,减载率最大值为0.329,脱轨系数最大值为0.108,车体竖向加速度最大值为1.103 m/s2,车体横向加速度最大值为0.486 m/s2,均满足表3二级管理时车辆动力响应的控制标准。舒适度指标最大为2.855,满足合格要求,对应组合工况为列车荷载+公路活载+降温作用引起的最小梁端折角。
结合10 m弦测值及车桥动力分析结果,所有的独立影响因素中,温度对大跨度桥梁梁端伸缩装置影响最大;在列车荷载+公路活载+温度作用引起最小梁端折角的组合工况下,车辆性能与轨道形位最不利。温度对梁端伸缩装置不仅是一种荷载,也起到改变伸缩装置状态的作用,不同温度变化对应不同的活动枕间距,如整体升温最大时活动枕间距最小。车桥耦合振动分析可以对梁端伸缩装置的性能起到验证的作用,车桥动力分析与10 m弦分析结果相匹配,证明了基于轨道形位对梁端伸缩装置性能进行评估的有效性、合理性。
4 结论
1)考虑到梁端伸缩装置附近区域的轨道平顺状态受到温度、横风、多线行车、病害等外部环境因素共同作用存在一定概率,本文对梁端伸缩装置的性能提出分级管理的原则,对上述环境因素采用不同的荷载组合及10 m弦、车辆动力响应控制建议值。
2)消除随机不平顺的影响后,梁端伸缩装置的轨道平顺状态可参考《高速铁路无砟轨道线路维修规则》采用10 m弦测值进行评定。
3)所有外部环境因素中,温度对大跨度桥梁梁端伸缩装置影响最大。列车荷载+公路活载+温度作用引起最小梁端折角的组合工况下,车辆性能与轨道形位最不利。
4)车桥动力分析与10 m弦测值分析的结果相匹配,证明了基于轨道形位对梁端伸缩装置性能进行评估的有效性、合理性。

