受压T肋被加劲板局部稳定试验与计算方法

赵秋 陈鹏 林楚 陈友杰

1.福州大学土木工程学院，福州350108；2.福州市建设发展集团有限公司，福州350108

T肋加劲板常应用于钢箱梁桥的受压翼缘，斜拉桥与悬索桥的钢塔以及钢箱拱桥的钢拱中。由于大跨度钢结构桥梁的普及，T肋加劲板须承受更大的轴向压力，因此受压稳定问题更加突出［1-3］。

目前，对于T肋被加劲板受压稳定研究相对较少，多数只研究闭口加劲肋形式下被加劲板的受压稳定性能。文献［4］对9块钢箱梁U肋加劲板进行轴压试验，其中有1块板件发生被加劲板的局部屈曲破坏，2块板件发生加劲肋与被加劲板的共同屈曲破坏。文献［5-6］通过轴压试验研究U肋被加劲板的局部失稳破坏，并采用受压柱理论研究其破坏机理。文献［7］针对U肋加劲板建立相应的局部稳定试件有限元模型，并通过试验验证该数值模拟方法的正确性。上述文献对闭口U肋加劲下被加劲板的研究较为完善。文献［8］通过建立数值模型对T肋加劲板在轴压状态下的稳定影响参数进行分析，发现T肋加劲板的稳定承载力随被加劲板几何初始缺陷半波数量的增加而降低。文献［9］对T肋加劲板进行建模，提出适用于高强度钢的加劲板面内抗压强度计算公式。

桥梁设计中，加劲肋通常设计为刚性加劲肋。被加劲板由于两端横隔板以及平面外加劲肋的存在，可视为四边简支板［10］。加劲板的局部稳定破坏通常是被加劲板发生局部屈曲，而局部稳定的研究是整体稳定或整体与局部相关稳定研究的基础。

本文对T肋加劲板中组成板件的被加劲板局部失稳进行试验研究，并通过有限元分析提出计算方法，为T肋被加劲板的受压稳定设计提供参考。

1 被加劲板局部稳定试验

1.1 试件设计

综合考虑工程常用的尺寸规格、试验条件以及试验目的，设计了T肋加劲板试件截面尺寸，长度取被加劲板宽度的3倍［11］，试件横截面见图1。改变被加劲板板宽度，试件参数见表1。

表1 被加劲板局部稳定试件参数

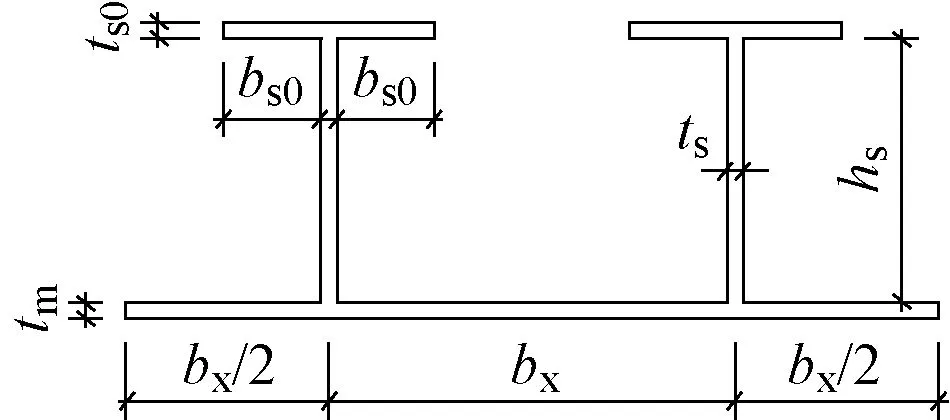
图1 被加劲板局部稳定试件横截面

根据GB/T 228.1—2010《金属材料拉伸试验第1部分》［12］，制作T肋加劲板局部稳定试验的标准拉伸试件。在试件中心设应变花，得到Q3、Q4类试件实际屈服强度分别为357，440 MPa，极限强度分别为454，543 MPa，弹性模量均为208 GPa。

1.2 试验方案

1.2.1 边界处理

为了正确模拟局部稳定试件在轴压作用下的试验边界，将试件两端的板件嵌入带有凹槽的钢板内，保证试件均匀受压且不发生滑移，使其处于简支约束下。开槽钢板的凹槽略大于试件横截面尺寸，并在钢板边缘位置开孔，保证螺栓可以穿过开孔与承压端板连接；承压端板是一块较厚的平整钢板，在与开槽钢板同样的开孔位置制作螺纹孔；开槽钢板和承压端板通过螺栓组成限位装置，见图2。

图2 被加劲板局部稳定试件限位装置

为保证被加劲板外侧悬臂钢板不会先发生变形，设计采用两块角钢夹住被加劲板的悬臂侧钢板，对悬臂侧钢板的面外刚度进行加劲，同时角钢不能接触到端板，不起分摊荷载的作用，见图3。

图3 试验加载

1.2.2 加载方案

试验加载设备采用最大试验力为10 000 kN的电液伺服长柱压力试验机。正式加载前应先进行预加载。预加载的荷载值为估算极限荷载值的10%～20%。预加载过程中，采用薄钢片对试件端部的平整度进行调整。预加载完成后卸去全部荷载，读数归零后正式加载。正式加载先采用荷载控制，每级加载值为100 kN，加载速率为1 kN/s。当荷载达到预估极限荷载的60%时，继续向千斤顶油缸送油，改用位移控制，加载速率为0.3 mm/s。在试验过程中分别采用DH3816静态应变采集系统定时采集试件的位移，采用试验机自带的荷载传感器采集试件的荷载。

1.2.3 测点布置与量测

被加劲板局部稳定试件上的测点主要包括轴向位移测点和应变测点（图4）。布置8个量程为100 mm的YHD-100型位移计，测试加劲板在荷载作用下的轴向位移。在加劲板L/4、L/2和3L/4截面处，沿横向在T肋与被加劲板相连位置和被加劲板中间分别布置应变片和应变花，测试被加劲板在荷载作用下的应变。在固定角钢的L/2截面处布置应变片，观测角钢的受力情况。每一个被加劲板局部稳定试件共需6片BX120-3CA型应变花，8片BX120-1AA型应变片。

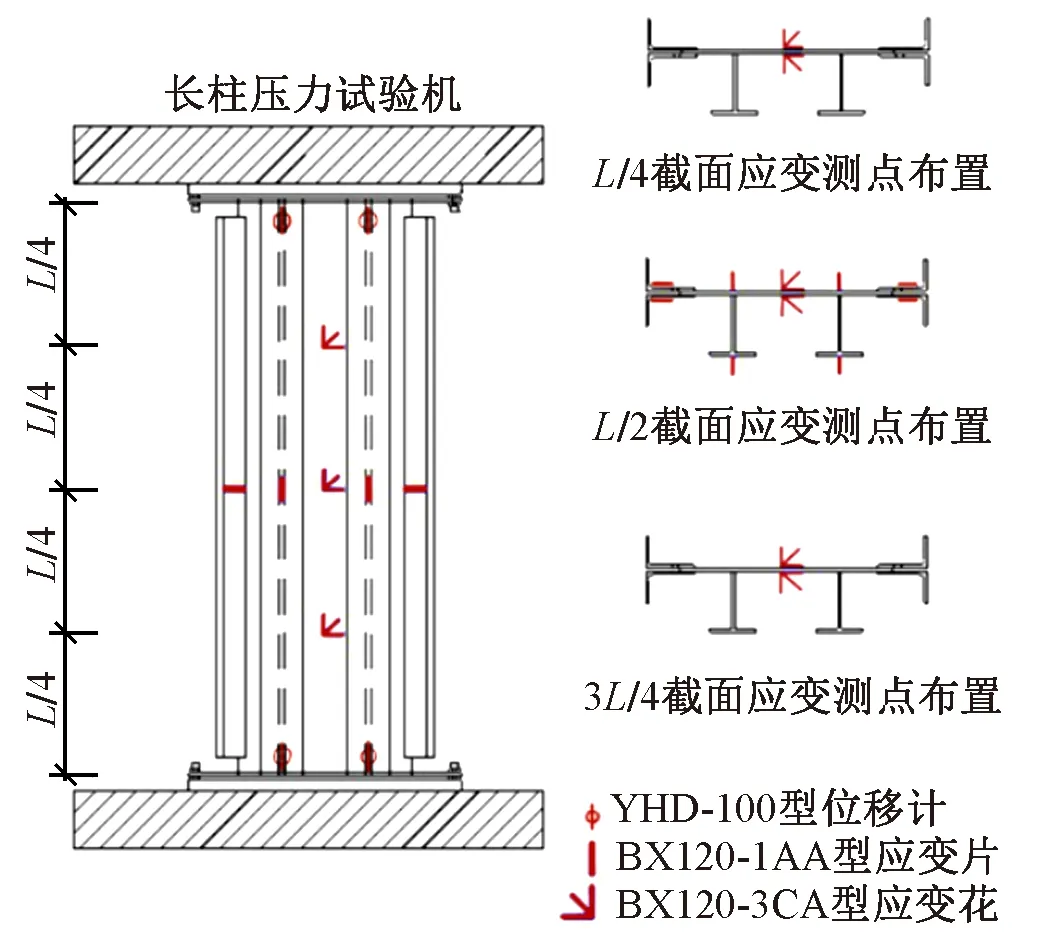
图4 试件测点布置

1.3 破坏现象分析

对被加劲板局部稳定试件变形部位和方向名称作统一规定，试件变形方向见图5。

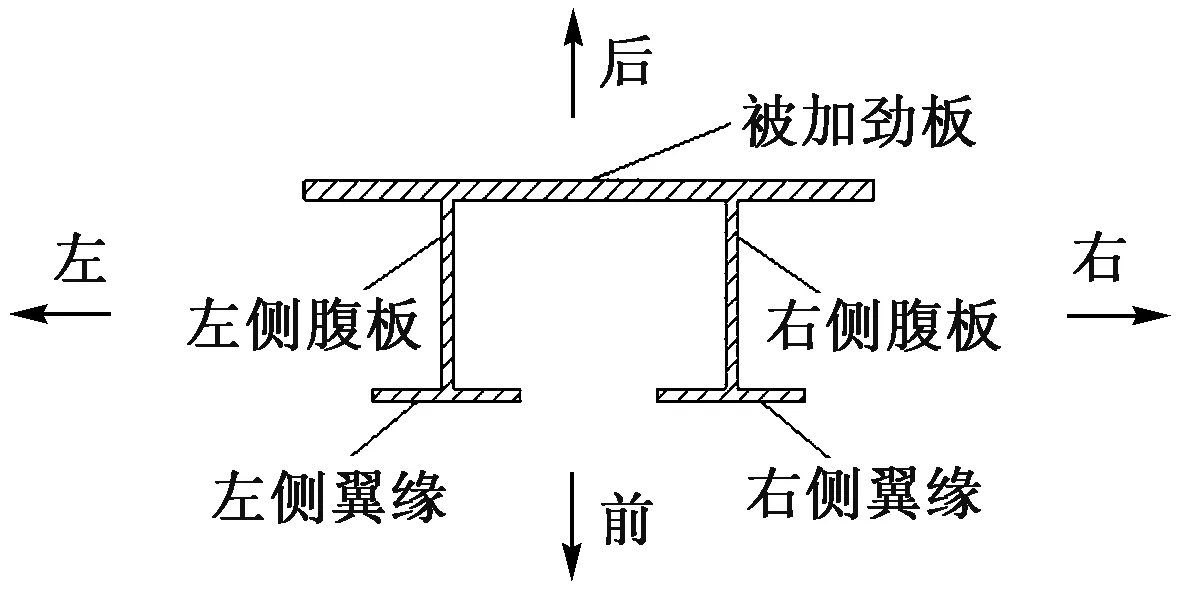
图5 试件变形方向

对于Q3-hm1试件，当荷载达到2 749.1 kN（68.4%Nd，Nd为峰值荷载）时，被加劲板L/2处首先产生了向前凸起的微小变形［图6（a）］；当荷载达到3 249.1 kN（80.9%Nd）时，被加劲板的变形逐渐增大，同时左侧翼缘的下端产生向后凹陷的微小变形；当荷载达到峰值荷载4 018.4 kN后下降到3 842.7 kN（95.6%Nd）停止加载。试件最终破坏时，在被加劲板的L/2处有一个向前的波峰，左侧翼缘的下端产生向后的微小变形，其他部位没有明显变形，见图6（b）和图6（c）。

图6 Q3-hm1试件破坏形态

对于Q3-hm2试件，当荷载达到3 110.4 kN（66.8%Nd）时，被加劲板2L/3处产生向前凸起的微小变形［图7（a）］；当荷载达到4 117.5 kN（88.4%Nd）时，被加劲板的变形逐渐增大；当荷载达到峰值荷载4 658.6 kN后下降到4 474.7 kN（96.1%Nd）停止加载。试件最终破坏时，被加劲板的2L/3处有一个向前的波峰，被加劲板左右悬臂侧的上端（没有被角钢固定的位置）均产生了向后的明显变形，见图7（b）和图7（c）。

图7 Q3-hm2试件破坏形态

对于Q4-hm1试件，当荷载达到3 280.8 kN（72.4%Nd）时，被加劲板2L/3处产生向前凸起的微小变形［图8（a）］；当荷载达到4 046.7 kN（89.4%Nd）时，被加劲板变形逐渐增大，同时左侧翼缘的上端产生向前的微小变形［图8（b）］；当荷载达到4 528.6 kN时，被加劲板2L/3处的变形更加明显［图8（c）］，此时伴随一声巨响，左侧的固定角钢顶部接触到了加载端板，荷载开始短暂上升，达到4 644.7 kN。为了不损坏机器，应停止加载。

图8 Q4-hm1试件破坏形态

对于Q4-hm2试件，当荷载达到3 604.3 kN（70.1%Nd）时，被加劲板2L/3处产生向前凸起的微小变形［图9（a）］；当荷载达到4 252.8 kN（82.7%Nd）时，被加劲板的变形逐渐增大；当荷载达到峰值荷载5 142.8 kN后下降到4 995.8 kN（97.1%Nd）停止加载。试件最终破坏时，被加劲板的2L/3处有一个向前的波峰，被加劲板左右悬臂侧的上端（没有被角钢固定的位置）均产生了向后的明显变形，见图9（b）和图9（c）。

图9 Q4-hm2试件破坏形态

综上所述，由于T形加劲肋的作用，4个试件的被加劲板均先于翼缘和腹板产生变形进而导致试件破坏。最早产生变形时的荷载为66.8%Nd～72.4Nd，位于试件L/2处（Q3-hm1试件）或2L/3处（Q3-hm2、Q4-hm1和Q4-hm2试件）。

根据试验现象将被加劲板局部稳定试件的破坏过程分为3个阶段（图10）：①未发生变形的阶段；②被加劲板L/2附近产生向前凸起的微小变形，其他部位没有产生变形；③被加劲板L/2附近变形明显，试件达到抗压承载力峰值。

图10 被加劲板局部稳定试件破坏过程

1.4 试验结果与分析

为了方便对比不同尺寸的被加劲板局部稳定试件的荷载-位移关系，将试验荷载和轴向位移分别除以试件实测横截面积和试件计算长度得到平均应力和平均应变，其关系曲线见图11。

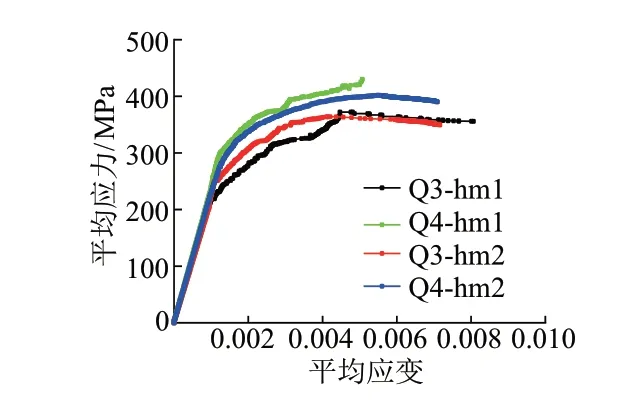
图11 试件平均应力-应变曲线

由图11可知，试件的平均应力-应变曲线经历了直线段、缓坡段、下降段3个主要阶段。直线段试件没有产生变形，平均应力和应变呈线性增长，应变变化较慢；缓坡段开始时被加劲板开始产生微小变形，随着荷载增大，变形逐渐增大，平均应变增长较快，斜率逐渐变小，曲线变得平缓，试件出现新的变形时斜率会减小得更快；下降段试件变形不断增大，曲线斜率为负，平均应力随着平均应变的增大而减小。

被加劲板试件试验结果见表2。结合表2和图11可知：①Q4类试件极限平均应力大于Q3类试件，即相同宽厚比的被加劲板局部稳定试件，材料强度越高，其极限承载能力越大。Q4类试件极限平均应力与屈服强度的比值小于Q3类试件，即相同宽厚比的被加劲板局部稳定试件，材料强度越高，其极限承载能力折减越大。②对于相同材料强度的被加劲板局部稳定试件，宽厚比越大其极限承载能力越小，且宽厚比为35的试件平均应力与极限平均应力的比值均小于宽厚比为25的试件，说明宽厚比越大，试件越早发生屈曲，局部屈曲之后强度的提升空间越大。

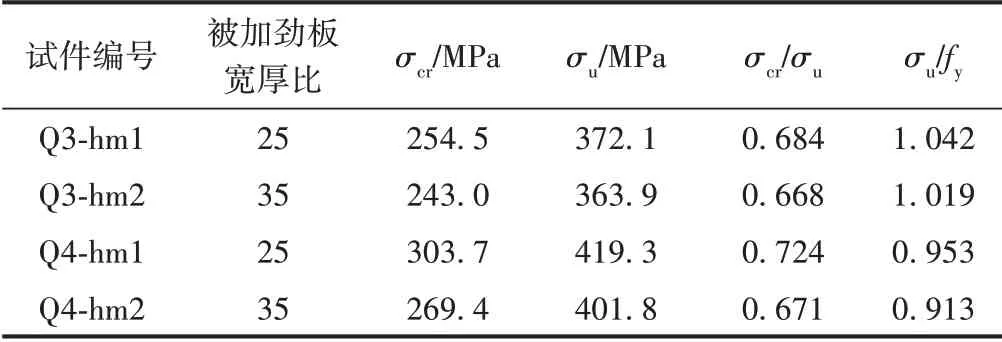
表2 被加劲板试件试验结果

2 有限元数值模拟方法验证

采用shell181单元建立有限元模型，采用多线性等向强化模型模拟大应变情况下的应力-应变关系。试验中限位板较好地约束了试件端部的非轴向位移，因此在有限元中将试件两端设置为固结支座约束。在试件两端截面的质心位置分别设置1个mass21单元主节点，然后把试件两端全部节点的自由度分别耦合到两端的主节点上。同时约束固定端所有的自由度，约束加载端除轴向位移以外的自由度。以初始应力的形式引入截面残余应力，残余应力采用文献［13］中T肋加劲板残余应力的实测值；局部初始几何缺陷采用试件的一阶屈曲变形，按固定比例计入，由于试件局部初始几何缺陷较大，保守取δ/b=1/100（δ为变形值，b为被加劲板宽度）。

2.1 破坏形式验证

判断有限元模型是否正确的一个重要指标就是破坏模式是否能与试验中的破坏模式吻合。不同试件破坏模式与有限元破坏模式对比见图12。图中的应力为von Mises应力。

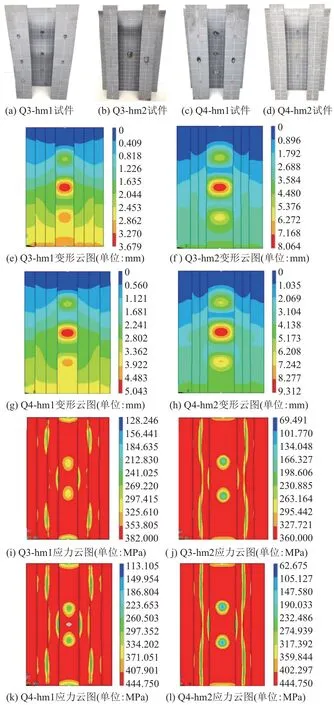
图12 不同试件破坏模式与有限元破坏模式对比

由图12可知：①4种试件与有限元模型均发生被加劲板的局部屈曲破坏，且在被加劲板L/2处先发生局部屈曲；②试件大部分位置达到了屈服强度，未达到屈服强度的范围随着被加劲板宽厚比的增大而增加，总体吻合情况良好。

2.2 极限承载力与平均应力-应变曲线验证

试件试验与有限元计算的平均应力-应变曲线对比见图13。可知：试验与有限元的平均应力-应变曲线基本相同，均表现为先直线上升，随着荷载增加曲线斜率逐渐减小，曲线继续上升达到峰值平均应力后开始下降，试件处于较好的轴压状态，基本没有发生偏心。Q4-hm1试件因角钢接触到加载端板提前结束试验，导致极限平均应力略小，其他试件极限平均应力有限元计算值均小于试验值。

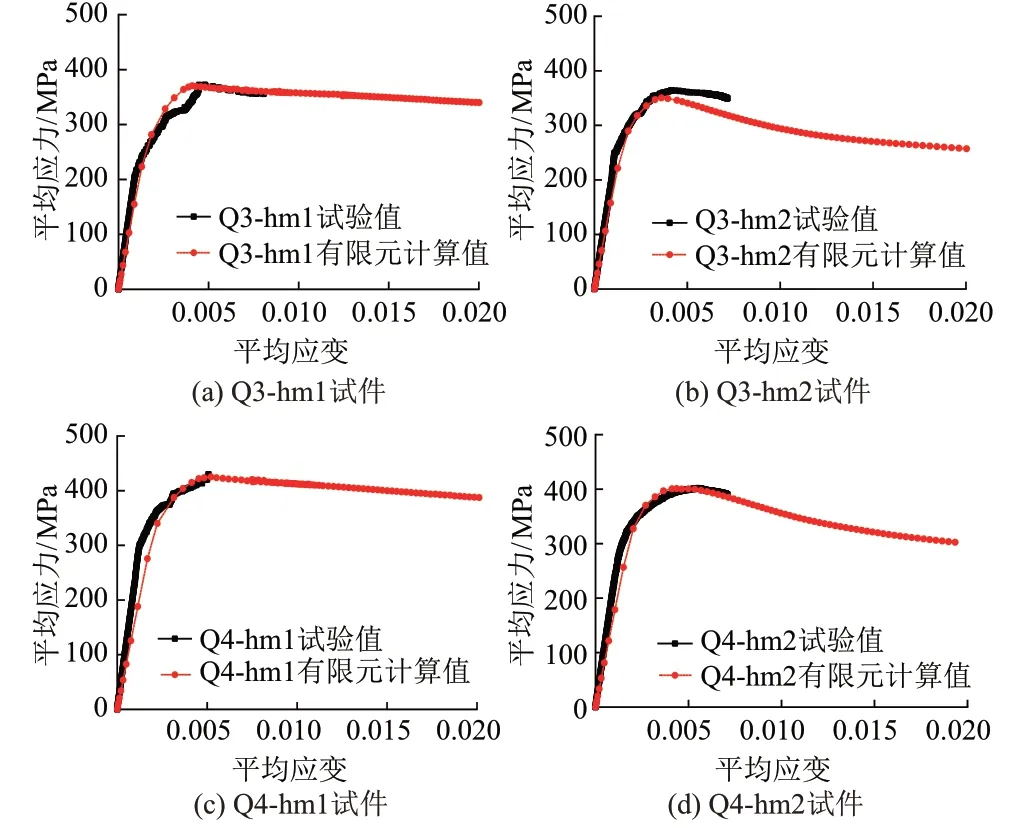
图13 试件试验与有限元计算的平均应力-应变曲线对比

极限承载力是T肋加劲板轴压构件最重要的性能指标。试件极限平均应力试验值与有限元计算值对比见表3。可知，试件极限平均应力试验值与有限元计算值比较接近，有限元计算值比试验值平均小0.73%。

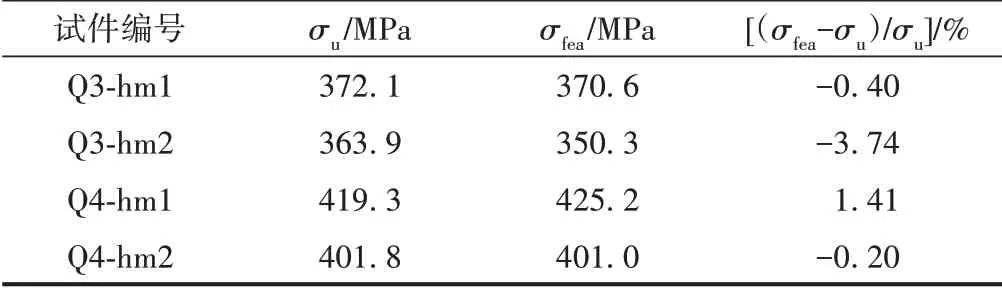
表3 试件极限平均应力试验值与有限元计算值对比

3 受压T肋被加劲板局部稳定分析

3.1 计算模型尺寸参数拟定

基于有限元数值分析模型对T肋被加劲板的局部屈曲性能进行参数化分析，研究材料本构模型、简化焊接残余应力和局部初始几何缺陷对局部屈曲性能的影响。模型以一个宽厚比较小的标准尺寸为基准，横向建立3个相同的T形加劲肋。为防止被加劲板两侧悬臂先发生失稳，采用与第2节相同的方法对被加劲板两侧悬臂进行约束。

被加劲板局部稳定计算模型包含6种模型尺寸，被加劲板的宽厚比范围取25～50，腹板的宽厚比为16，翼缘的宽厚比为6。模型的长度取被加劲板宽度的3倍。其中M-25和M-35计算模型的尺寸分别为Q3-hm1和Q3-hm2试件的尺寸。被加劲板局部稳定计算模型横截面与参数分别见图14和表4。

图14 被加劲板局部稳定计算模型横截面

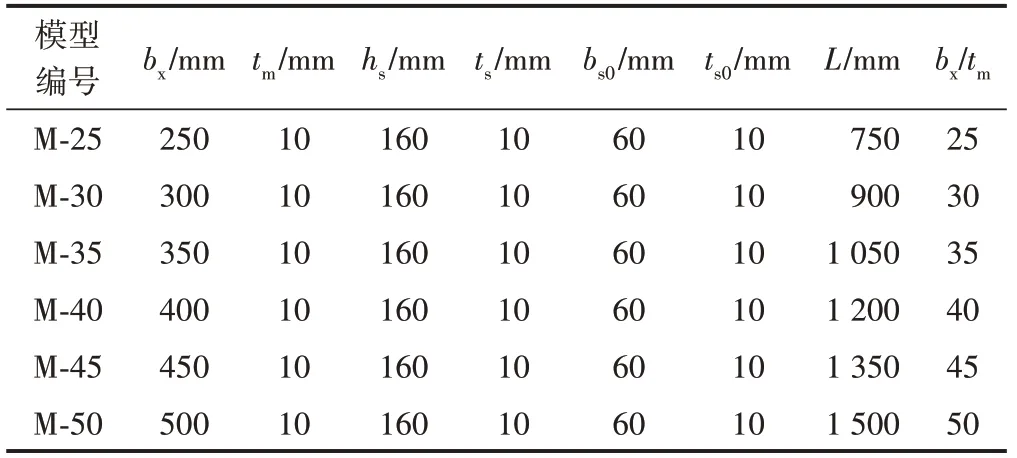
表4 被加劲板局部稳定计算模型参数

3.2 本构模型的影响

本构关系仅考虑钢材Q345强度的情况。为对比不同本构模型对数值模拟结果的影响，采用四折线本构模型、理想弹塑性本构模型、切线模量为弹性模量1%的两折线本构模型（简称1%切线模型）和切线模量为弹性模量3%的两折线本构模型（简称3%切线模型）分别进行建模计算。4种本构模型见图15。

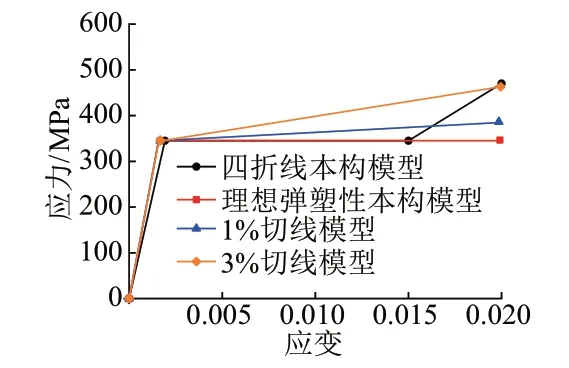
图15 4种本构模型

有限元模型暂不计入残余应力的影响，对于局部初始几何缺陷，取一阶屈曲模态下被加劲板宽度的1/200。4种本构模型下稳定系数对比见图16。可知，被加劲板局部失稳计算模型采用理想弹塑性本构模型的稳定系数与采用四折线本构模型的稳定系数基本相同；采用1%切线模型的稳定系数略大于采用四折线本构模型的稳定系数，二者的差值随宽厚比的增大而减小；采用3%切线模型的稳定系数明显大于另外3种本构模型的稳定系数，与四折线本构模型稳定系数的差值随宽厚比的增大而减小。因此，偏安全地采用理想弹塑性本构模型来计算局部稳定模型的稳定系数。

图16 4种本构模型下稳定系数对比

3.3 焊接残余应力

3.3.1 简化残余应力分布与验证

计算模型对残余应力采用以折代曲的简化方式［13］（图17）。图中，lm，c-t为过渡区长度。通过盲孔法对T肋被加劲板的残余应力进行试验，并建立对应的有限元模型验证数值模拟方法的正确性。

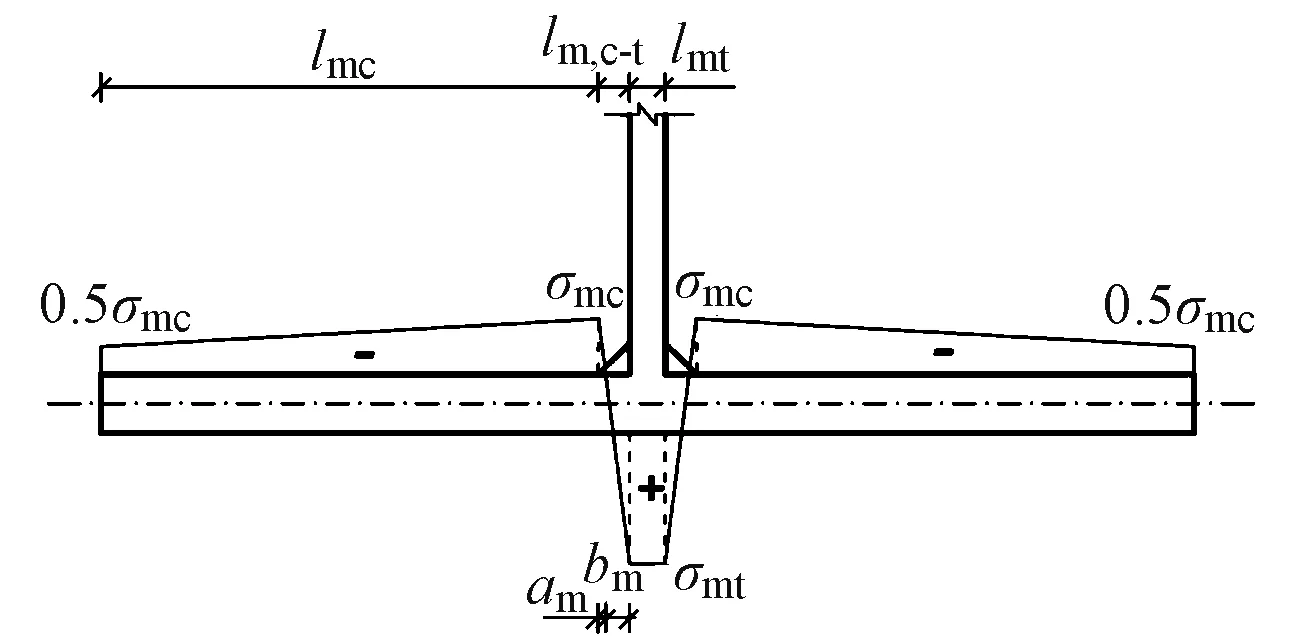
图17 被加劲板残余应力简化分布形式

利用残余应力的自平衡原理得到T肋被加劲板的残余应力简化分布方式，通过式（1）解得残余应力分布的相关参数am、bm。其中，am与bm通过相似三角形可简化为一个变量进行求解。

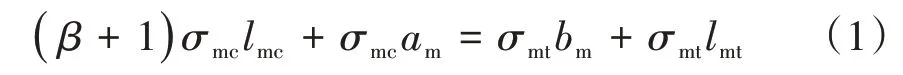
式中：β为残余压应力修正系数；σmt为被加劲板残余拉应力，取被加劲板屈服强度fy；σmc为被加劲板残余压应力，取σmc=amfy/bm；am和bm分别为过渡区压、拉应力长度；lmc和lmt分别为压、拉应力分布长度。

在被加劲板局部稳定试验中取Q3-hm1、Q4-hm1试件，在相同局部初始几何缺陷情况下分析数值模拟和简化残余应力分布对试件承载力的影响，见图18。可知，两种残余应力分布方式所得平均应力-应变曲线基本重合。因此，可使用简化残余应力分布来分析受压T肋被加劲板局部稳定性能。

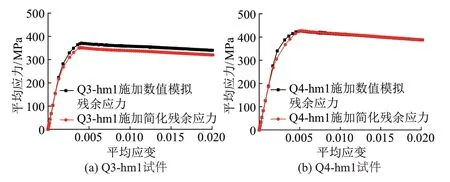
图18 两种残余应力分布对试件承载力的影响曲线

3.3.2 计入简化残余应力对稳定系数的影响

对6个不同尺寸的被加劲板计算模型分别计入简化残余应力，残余应力对稳定系数的影响曲线见图19。可知，计入简化残余应力的稳定系数小于不计入残余应力的稳定系数，且随宽厚比的增大，稳定系数的减小幅度逐渐增大。

图19 残余应力对稳定系数的影响曲线

3.4 局部初始几何缺陷的影响

为研究局部初始几何缺陷位置对被加劲板局部稳定性能的影响，采用一致缺陷模态法，取宽厚比最大的M-50模型，计算分别在不同子板件处计入局部初始几何缺陷后的稳定系数，并绘制应力-应变曲线，见图20。不同局部初始几何缺陷位置对应的稳定系数见表5。

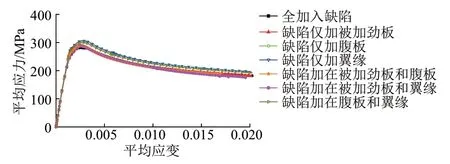
图20 M-50模型平均应力-应变曲线对比

表5 不同局部初始几何缺陷位置对应的稳定系数

由图20和表5可知：①不同局部初始几何缺陷位置的平均应力-应变曲线总体趋势相同；②最先发生局部失稳的是被加劲板，当缺陷施加在被加劲板上时，稳定系数比仅施加在腹板、翼缘时更小；③当被加劲板计入局部初始几何缺陷时，构件轴向刚度减小得快，极限平均应力逐渐减小；④当所有板件均计入局部初始几何缺陷时，稳定系数最小，对构件的稳定性能最不利。因此，下文均采用构件的子板件全部计入局部初始几何缺陷来计算模型的稳定系数。

分别计入4种局部初始几何缺陷幅值（B/50，B/100，B/200，B/300，B为各个被加劲板最大板宽），研究其对被加劲板局部稳定性能的影响，见图21。可知，局部初始几何缺陷幅值为B/50的稳定系数最小；被加劲板宽厚比为35时，稳定系数变化幅度最大；稳定系数的变化幅度随宽厚比的增大而先增大后减小。宽厚比较大时，增大局部初始几何缺陷的幅值对稳定系数影响较小，原因是极限承载能力在宽厚比较大时已经由于子板件局部失稳而显著削弱。

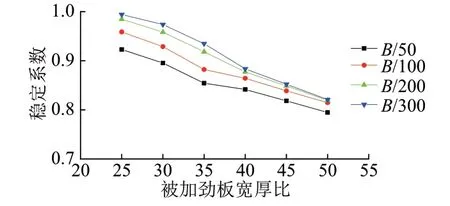
图21 不同初始几何缺陷幅值对稳定系数的影响曲线

4 被加劲板局部稳定系数计算方法

4.1 被加劲板局部稳定系数简化计算公式

为了解被加劲板的屈曲性能和屈曲后强度利用情况，采用改变被加劲板宽度和厚度的方式得到仅被加劲板发生局部失稳时的受压局部稳定系数。被加劲板宽度为300～700 mm，厚度为10～28 mm；T肋腹板的高度和宽度分别取250，10 mm；T肋翼缘的宽度和厚度分别取80，10 mm。钢材强度选取常用的Q345和Q420。两种钢材强度的模型各有42个，通过建立有限元模型计算板件的相对宽厚比和局部稳定系数，模型采用理想弹塑性本构模型，边界条件、残余应力的计入与本文第3节中的方法相同，局部初始几何缺陷按最大被加劲板宽度的1/200计入。

对被加劲板局部稳定模型的计算结果分别采用多项式和Perry公式进行拟合。多项式拟合曲线的计算公式见式（2）和式（3）。

Perry公式拟合曲线的计算公式见式（4）和式（5）。

被加劲板局部稳定拟合曲线对比见图22。

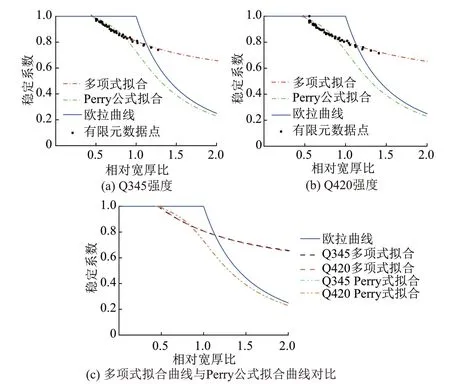
图22 被加劲板局部稳定拟合曲线对比

由图22（a）和图22（b）可知：①Q345强度的多项式拟合曲线稳定系数开始发生折减的相对宽厚比为0.46，略小于Q420强度开始折减的相对宽厚比0.49。多项式拟合曲线与有限元数据点整体吻合较好，在相对宽厚比达到1.14后大于欧拉曲线，说明被加劲板开始利用屈曲后强度。②Q345强度的Perry公式拟合曲线稳定系数开始发生折减的相对宽厚比为0.44，略小于Q420强度开始折减的相对宽厚比0.45，且不考虑屈曲后强度。③不同强度的Perry公式拟合曲线在相对宽厚比小于0.93时与有限元数据点吻合良好，当相对宽厚比大于0.93时Perry公式拟合曲线下降较快，直至相对宽厚比为2.0时也未大于欧拉曲线。

由图22（c）可知：不同钢材强度的多项式和Perry公式拟合曲线整体变化趋势基本相同，说明不同钢材强度对稳定系数的影响较小；Perry公式拟合曲线比多项式拟合曲线更早开始折减。在相对宽厚比小于0.84时，Perry公式拟合曲线得到的稳定系数大于多项式拟合曲线得到的稳定系数，当相对宽厚比大于0.84时规律相反；多项式拟合曲线在相对宽厚比大于1.14后大于欧拉曲线。因此，相比于多项式拟合曲线，Perry公式拟合曲线不考虑屈曲后强度更加安全。

4.2 被加劲板稳定系数折减曲线对比

将被加劲板局部稳定系数简化公式与JTG D64—2015《公路钢结构桥梁设计规范》［14］（简称中国规范）、日本道路桥示方书［15］、美国规范AASHTO［16］和欧洲规范EUROCODE［17］相关规定曲线进行对比，见图23。

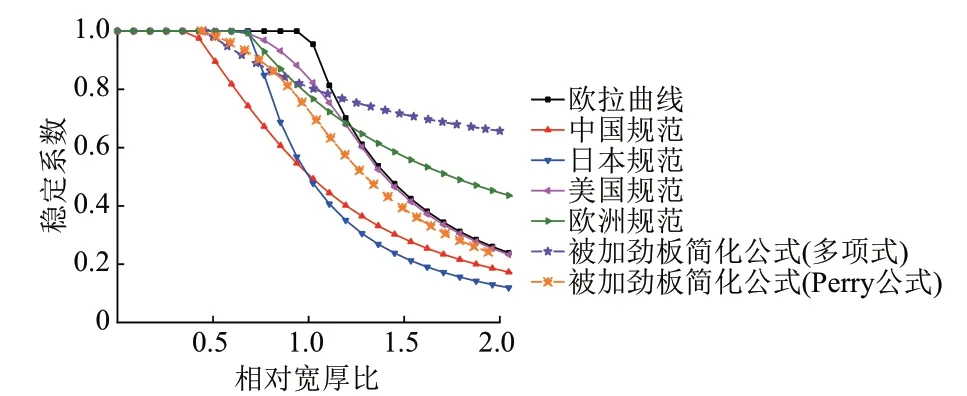
图23 局部稳定系数折减曲线与各国规范曲线对比

由图23可知：

1）中国规范、日本规范和美国规范的局部稳定系数折减曲线均在欧拉曲线的下方，表明这些规范不允许加劲肋之间的板件发生局部屈曲。

2）中国规范曲线开始折减的宽厚比小于日本规范曲线开始折减的相对宽厚比，在相对宽厚比小于1.0时，中国规范曲线折减较快，且位于日本规范曲线下方；当相对宽厚比大于1.0时，日本规范曲线折减极快，中国规范曲线位于日本规范曲线的上方。说明中国规范在相对宽厚比较小时比较保守，日本规范不推荐使用相对宽厚比较大的构件。

3）欧洲规范曲线开始折减的相对宽厚比较大，在相对宽厚比大于1.2时稳定系数大于欧拉曲线，说明欧洲规范允许加劲肋之间的板件发生局部屈曲，当相对宽厚比较大时可以利用构件的屈曲后强度。

4）多项式拟合曲线在相对宽厚比较大时也利用了屈曲后强度，因此将其与欧洲规范曲线进行对比。可以看出，多项式拟合曲线开始折减时的相对宽厚比小于欧洲规范开始折减的相对宽厚比。随着相对宽厚比增加，多项式拟合曲线折减较慢，逐渐高于欧洲规范曲线。

5）Perry公式拟合曲线没有考虑利用屈曲后强度，因此将其分别与中国规范、美国规范和日本规范曲线进行比较。Perry公式拟合曲线开始发生折减的相对宽厚比大于中国规范曲线开始折减的相对宽厚比，小于美国规范和日本规范曲线开始折减的相对宽厚比。Perry公式拟合曲线整体介于中国规范曲线与美国规范曲线之间，与美国规范曲线更接近。因此，可以偏安全地采用Perry公式拟合曲线进行计算。

5 结论

1）T肋被加劲板局部稳定试验中所有试件均发生了被加劲板的局部失稳，被加劲板宽厚比越大，试件越早出现局部屈曲变形，极限承载能力折减越大，局部屈曲之后强度的提升空间越大。

2）有限元计算模型采用理想弹塑性本构模型模拟，并计入已验证的简化残余应力，子板件全部计入局部初始几何缺陷，其中局部初始几何缺陷取板宽的1/200。有限元计算值与试验值吻合情况良好。

3）被加劲板相对宽厚比越大，稳定系数折减得越多，稳定系数折减的幅度在计入局部初始几何缺陷时呈现先增大后减小的趋势，且当局部初始几何缺陷施加在最先发生局部失稳的子板件上时，稳定系数折减得较明显。

4）钢材强度对被加劲板局部稳定系数影响较小，随着相对宽厚比增加，多项式拟合曲线逐渐高于欧洲规范曲线，考虑板件屈曲后强度；而采用Perry公式拟合曲线整体均位于欧拉曲线的下方，介于中国规范曲线与美国规范曲线之间，不考虑板件屈曲后强度。因此，可以偏安全地采用Perry公式拟合曲线进行计算。