基于耦合振动的高速磁浮轨道梁横向刚度研究

王淼 宋振森 滕念管

1.上海交通大学船舶海洋与建筑工程学院，上海200240；2.上海市公共建筑和基础设施数字化运维重点实验室，上海200240

开发时速600以上的高速磁浮轨道交通系统可为中长距离旅客运输提供安全、舒适、高速的交通方式。该系统中土建部分占总造价的60%～80%［1-2］。由于线路设计中多采用以桥代路的方案，磁浮列车与轨道梁在轨道不平顺及风荷载作用下会产生横向耦合振动，若轨道梁结构设计不合理则可能产生较大的振动或共振，导致功能件损伤、混凝土开裂，危及系统安全性。因此，有必要建立车桥横向耦合振动模型，研究轨道梁截面参数对系统横向动力性能的影响。

高速磁浮列车采用自动控制器对磁浮力进行反馈控制，将悬浮、导向磁浮间隙控制在（10±2）mm内，进而实现列车的悬浮与导向。文献［3］建立了考虑控制系统的车-连续梁竖向耦合振动模型，指出轨道梁加速度是结构的主要控制因素之一。文献［4］通过竖向耦合振动数值模拟，指出轨道梁挠度比对磁浮间隙有决定性影响。文献［5］基于模型修正法进行了竖向耦合振动分析，研究表明轨道不平顺对系统加速度响应有重要影响。文献［6］在Simpack上建立了车辆的横向振动模型，重点关注了车辆动力特性，表明高速磁浮横向、竖向振动是弱耦合的。目前，关于磁浮振动的研究主要侧重于竖向耦合振动，而对系统的横向耦合振动则关注较少。

TB 10630—2019《磁浮铁路技术标准（试行）》规定当轨道梁的竖向一阶自振频率大于1.1倍车速与跨度之比时，可不进行车桥耦合动力响应分析，但未对轨道梁的横向动力性能做出要求。因此，若提高设计时速，须相应增加轨道梁的一阶竖向自振频率。当轨道梁长度一定时，自振频率与刚度正相关、与单位长度质量负相关［7］。针对与时速600磁浮配套的轨道梁结构，较为经济的设计思路是基于上海磁浮轨道梁截面形式，保持截面面积一定，通过对截面进行优化设计进而提高竖向自振频率，即“面积不变、增加高度”的优化方式，但这种方式会导致轨道梁的横向刚度降低，对系统横向动力学性能产生不利影响。因此，本文针对这一问题，通过耦合振动分析，探究横向刚度降低后系统的动力响应规律，明确轨道梁横向刚度对高速磁浮横向动力学性能的影响。

1 车桥耦合振动模型

1.1 模型概述

高速磁浮列车具有横向、竖向振动弱耦合的特点［6］，其走行部设有防侧滚稳定装置，与空气弹簧提供的抗侧滚刚度共同作用来防止车体过大的侧滚运动［8］。在列车走行部中，分别设有独立的悬浮和导向电磁铁提供车辆的悬浮、导向力。在二系悬挂中，由摆杆提供横向刚度，由空气弹簧提供竖向刚度。

磁浮列车-轨道梁耦合系统的激振因素主要有轨道不平顺、侧向风荷载、列车偏载等。本文主要分析轨道梁横向刚度参数的影响，因此以横向轨道不平顺和风致横向荷载为激振源进行研究。

将车体、悬浮架和导向电磁铁视为刚体，并考虑水平方向的横移、摆头运动。5节编组的列车共有246个自由度，按qV1～qV246编号。为便于区分，奇数为横移自由度，偶数为摆头自由度。采用弹簧阻尼器模拟摆杆及橡胶弹簧的横向回复力；基于比例-微分（Proportion Differentiation，PD）控制算法模拟电磁力，横向磁浮间隙控制在10 mm，并将振动幅值控制在2 mm以下。横向耦合振动计算简图见图1。

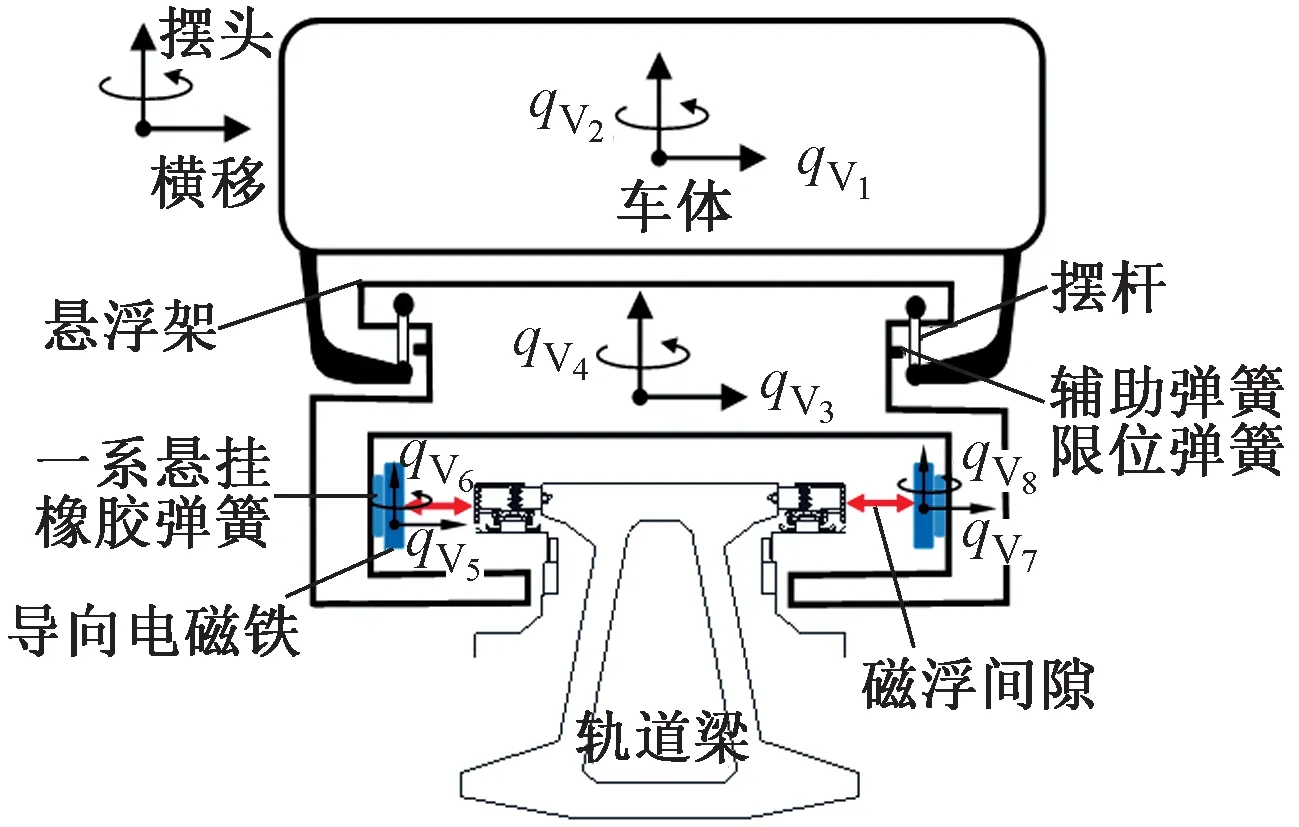
图1 横向耦合振动计算简图

轨道梁（图2）在移动的水平、竖向电磁力作用下产生振动，磁浮列车则在二者的作用下实现稳定的导向与悬浮。在列车运行中，轨道不平顺对磁浮间隙造成扰动，为了稳定磁浮间隙，电磁铁与轨道间的控制器产生了电磁力，并作用于列车与轨道梁，使二者产生振动，加剧了磁浮间隙波动，因此磁浮列车与轨道梁是一个耦合系统。竖向磁浮力提供列车的悬浮力，与列车自重平衡；水平横向电磁力提供导向力，仅在磁浮间隙受到扰动时产生。轨道梁采用闭口截面形式，且支座提供较大的抗扭刚度，因此轨道梁扭转振动幅值较小，轨道梁具有横向、竖向振动弱耦合的性质。为充分反映横向不平顺的随机性，综合考虑模型准确性与计算效率，建立了5列编组列车与40跨简支轨道梁的横向耦合振动模型进行数值研究。

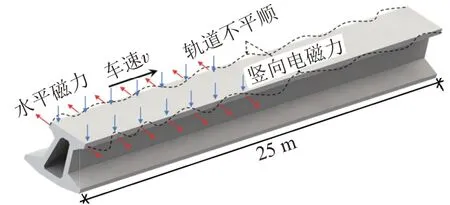
图2 轨道梁

1.2 耦合振动方程组

基于多刚体动力学，磁浮车辆的振动微分方程组可表示为矩阵形式，即

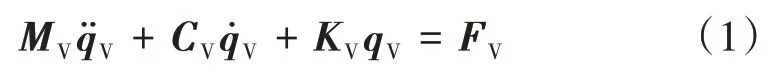
式中：MV为梁质量矩阵；qV为广义自由度列向量，是求解对象；CV为阻尼矩阵；KV为刚度矩阵；FV为广义力列向量，是磁浮力fmi的函数。

将轨道梁视为Euler-Bernoulli梁，基于模态叠加法考虑轨道梁前6阶模态，其振动微分方程为

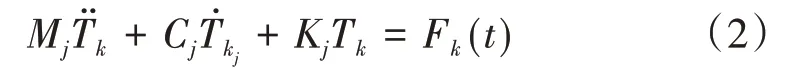
式中：k为轨道梁编号，取1～40；j为模态编号，取1～6；Mj为广义质量；Cj为广义阻尼；Kj为广义刚度；Tk为广义自由度，是求解对象；Fk(t)为广义力。

Fk(t)的表达式为

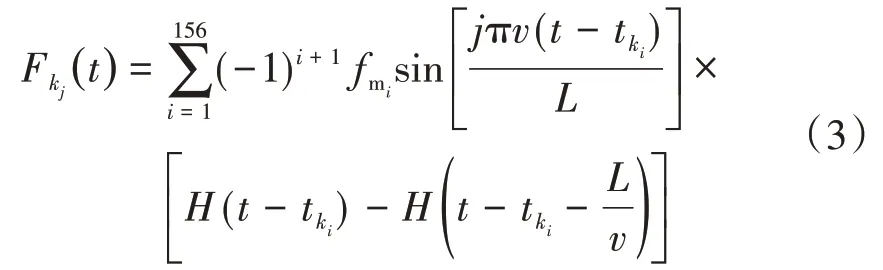
式中：fmi为第i个磁浮力，在每个电磁铁的三等分处布置1个集中荷载，共布置156个集中荷载模拟均布电磁力；v为车速；t为时间；tki为第i个磁浮力开始进入第k跨梁的时间；L为轨道梁跨度；H（·）为单位阶跃函数。

假设控制器的时滞满足稳定性要求，则PD控制算法的电磁力表达式为

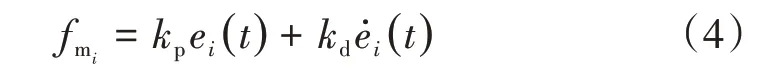
式中：kp、kd分别为比例系数和微分系数；ei(t)为第i个磁浮力所在位置的磁浮间隙。

ei(t)为电磁铁位移[qj(t)+li qk(t)]、轨道梁位移di(t)和轨道不平顺yri(t)的代数和，即

式中：li为第i个电磁力对其所在电磁铁质心的力臂；qj(t)、qk(t)分别为该电磁铁的平移、摆头自由度。

轨道梁位移di(t)可表示为

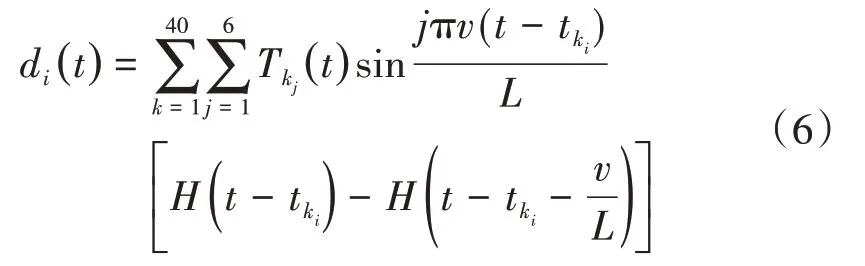
由于高速磁浮开通里程较少，未见相关的几何不平顺谱文献，故参考我国高速铁路不平顺谱中的轨距不平顺和方向不平顺谱，采用三角级数法［10］进行时域反演，得到横向轨道不平顺，见图3。

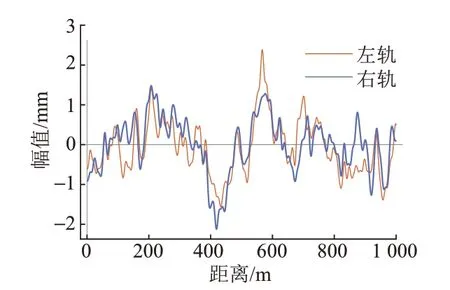
图3 横向轨道不平顺

将（4）式分别代入式（1）和式（2）消去fmi，则式（1）、式（2）、式（5）构成基于PD控制算法的列车-柔性轨道梁微分-代数方程组，指标为1，其中式（5）为代数方程。引入状态变量后可写为如下形式

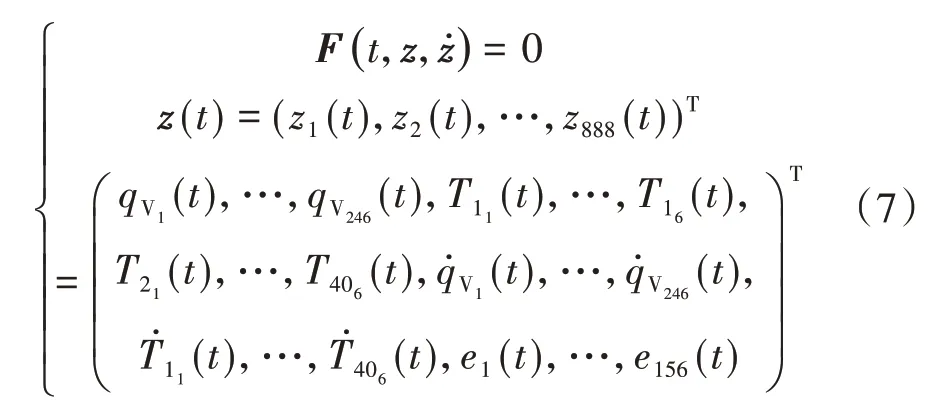
式中：z(t)为状态变量；zi(t)为向量元素。

本文采用软件Mathematica内置的隐式-微分代数求解器（Implicit Differential-Algebraic Solver，IDA）［10］进行数值求解，得到系统的耦合振动响应。

2 轨道梁横向刚度参数分析

车速与跨度之比（v/L）广义上视为列车通过频率，参考上海磁浮轨道梁截面形式，采用“面积不变，增加高度”的优化思路时，跨度L、截面面积A及密度ρ均为常数，速度提高至600 km/h时，令列车通过频率等于轨道梁固有频率，则

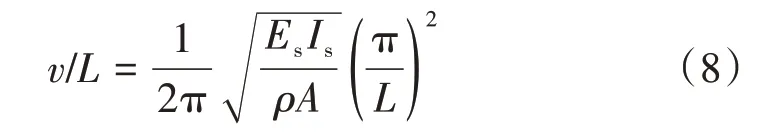
式中：Es为轨道梁的特征弹性模量；Is为绕竖轴的特征转动惯量。

令ρA=5 500 kg/m，L=25 m，根据式（8）可得特征刚度EsIs=4.0×1010N·m2。引入刚度比λ，则有

式中：El为轨道梁弹性模量；Il为绕竖轴转动惯量。

轨道梁计算参数见表1。

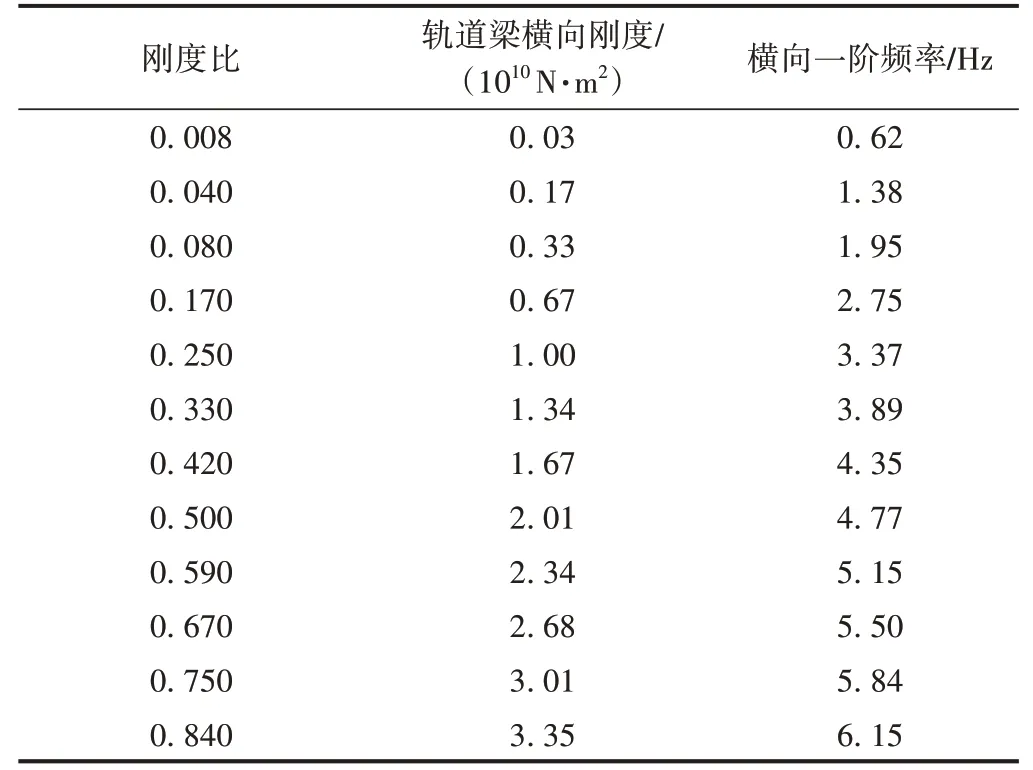
表1 轨道梁计算参数

列车在水平横向主要受轨道不平顺、侧向风荷载等激励产生振动。其中，轨道不平顺是由于施工误差、路基沉降、温度变形等原因造成，在磁浮列车运行中轨道不平顺会持续对磁浮间隙造成扰动。风荷载为作用于车辆上的偶然荷载，当风力等级较高时会对系统产生不可忽视的扰动。因此，根据实际工程情况建立耦合振动仿真模型，分析两种工况下轨道梁横向刚度参数对磁浮系统横向振动响应的影响：工况1，单独轨道不平顺作用；工况2，风速为20 m/s风致横向荷载及不平顺共同作用。

2.1 工况1

选取具有较大振动响应的第10跨梁进行分析，其在不同刚度条件下的跨中位移时程曲线见图4。可知，轨道梁在列车上桥后受磁浮力激励开始振动，并在下桥后振动逐渐衰减。随着λ减小，振动幅值增加，频率降低，振动衰减时间增加。

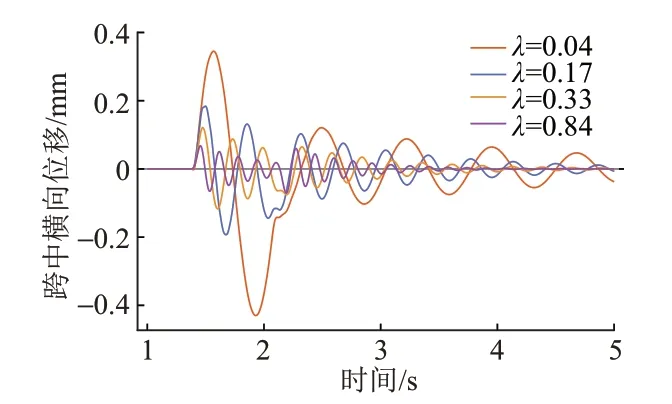
图4 工况1第10跨梁位移时程曲线

工况1最大磁浮间隙与刚度比的关系见图5。可知，将曲线从右至左划分为3个阶段：当λ＞0.42时，磁浮间隙对刚度比变化基本不敏感，车体前后端部的磁浮间隙略大于中部磁浮间隙，差值约为0.5 mm；当0.10＜λ＜0.42时，头车和尾车中部、尾车端部磁浮间隙随刚度比降低略有增加，列车各位置的磁浮间隙保持在1.7～1.8 mm；当λ＜0.1时，轨道梁刚度过小，列车经过对轨道梁产生了较大的扰动，导致尾部磁浮间隙急剧增加。

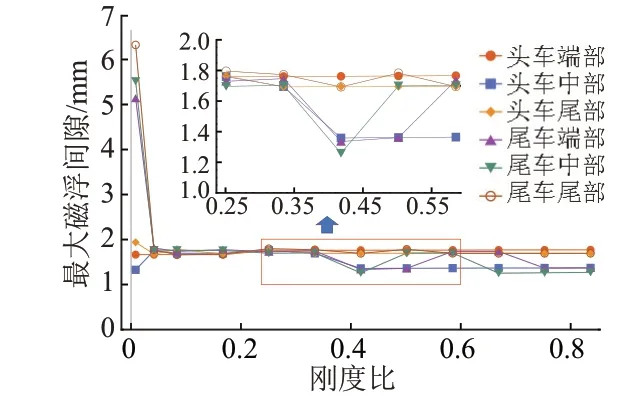
图5 工况1最大磁浮间隙与刚度比的关系

工况1轨道梁最大横向位移与刚度比的关系见图6。可知，由于不平顺的随机横向性，各跨梁的最大位移幅值具有离散性，整体上最大横向位移与刚度比成明显的负相关关系。当λ＞0.42时，最大位移小于0.1 mm，且不随刚度比产生明显变化，轨道梁具有优良的动力学性能；当λ＜0.42时，刚度越小，最大横向位移越有呈指数形式增加的趋势。

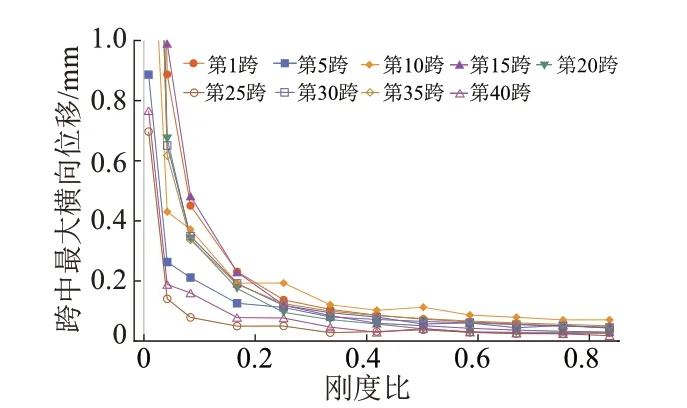
图6 工况1轨道梁最大位移与刚度比的关系

工况1轨道梁最大加速度与刚度比的关系见图7。可知：当λ＞0.33时，随着刚度比的减小，轨道梁频率降低，跨中最大加速度整体略有降低；当λ＜0.33时，随着刚度比的减小，跨中最大加速度整体呈增加趋势，但均小于0.15 m/s2。

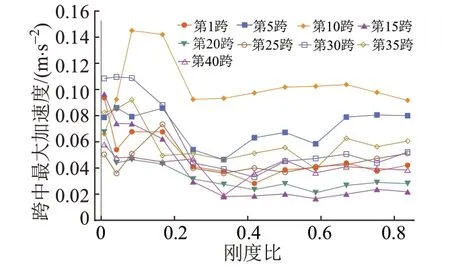
图7 工况1轨道梁最大加速度与刚度比的关系

轨道梁应具有足够的刚度，保证磁浮间隙、跨中位移、跨中加速度处于合理区间，确保系统的整体安全性。因此，刚度比以0.42为系统安全性分界点，即ElIl＞0.42EsIs时，磁浮间隙、轨道梁振动均对刚度变化不敏感。

2.2 工况2

工况2第10跨梁横向位移时程曲线见图8。可知，工况2中轨道梁跨中振动响应幅值比工况1显著增加。对比图4发现，λ=0.04时，跨中最大位移由0.35 mm上升至3.30 mm，表明轨道梁跨中振动响应对刚度比的敏感性显著加强，风致横向荷载明显放大了横向刚度降低所造成的不利影响，成为磁浮系统在水平横向的主要激振因素。

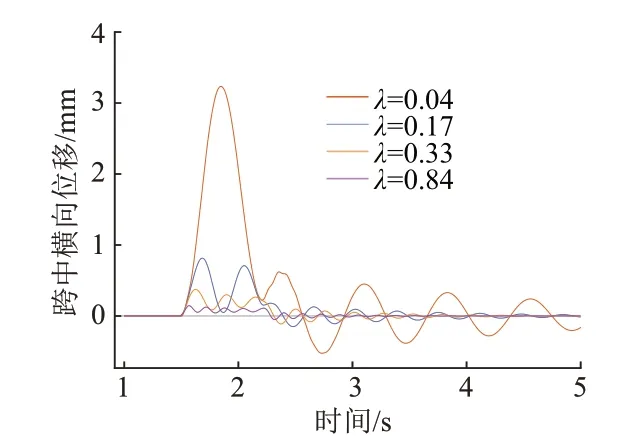
图8 工况2第10跨梁横向位移时程曲线

工况2最大磁浮间隙与刚度比的关系见图9。可知，λ＞0.42时，随刚度比变化，各磁浮间隙近似保持为平行直线，表明在此区间内，磁浮间隙对刚度比不敏感；λ＜0.42时，随着刚度比的减小，各磁浮间隙产生了较大的波动，λ＜0.25时迅速增加，在λ=0.008时达到20 mm。在实际工程中磁浮间隙为10 mm时电磁铁与导向面已接触，系统丧失稳定性。由于风致横向荷载的作用，磁浮间隙最大值比工况1显著提高，且车辆端部的电磁铁超过了2 mm，但中部电磁铁在刚度比大于0.5时仍处于容许范围。原因是横向荷载作用下，由于轨道梁振动增加，耦合振动会导致列车做摆头运动，因而每节车前后端部的磁浮间隙波动幅值大于车体中部的磁浮间隙，且尾车尾部磁浮间隙波动幅值最大。

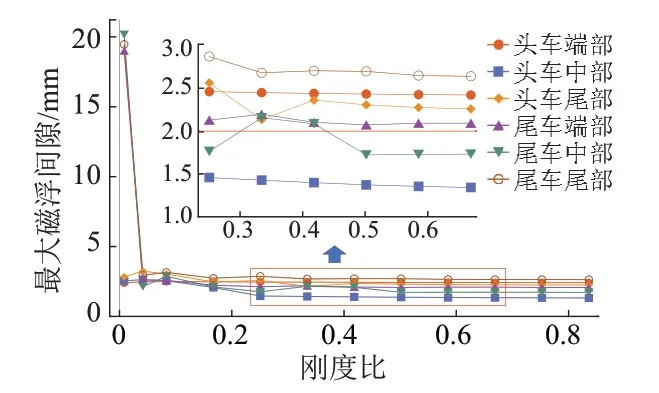
图9 工况2最大磁浮间隙与刚度比的关系

工况2轨道梁最大横向位移与刚度比的关系见图10。对比图6可知，工况2中各跨梁的振动响应离散程度降低，跨中最大横向位移与刚度比成强负相关关系，刚度比降低时跨中最大位移呈指数形式增加。当λ＞0.42时跨中最大横向位移均小于0.35 mm，其动力学性能满足要求。

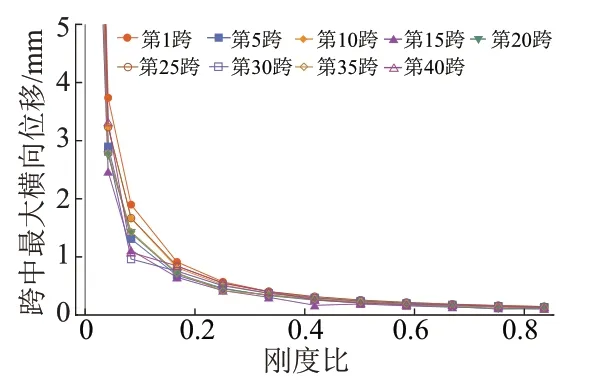
图10 工况2轨道梁最大横向位移与刚度比的关系

工况2轨道梁最大加速度与刚度比的关系见图11。对比图7可知，各跨梁最大加速度幅值的离散性显著降低，随刚度变化的规律更为明显。0.33＜λ＜0.84时，跨中加速度在0.04～0.16 m/s2波动，并在λ=0.50时取得极大值；λ＜0.33时，随着刚度降低，加速度幅值波动上升。

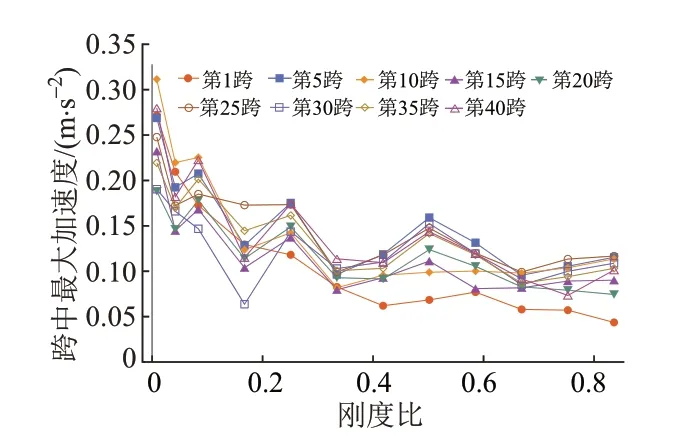
图11 工况2轨道梁最大加速度与刚度比的关系

综上所述，λ＞0.42时，2种工况下磁浮间隙、跨中位移、跨中加速度对刚度比不敏感，表明轨道梁横向刚度在此区间内横向动力学性能满足要求。

3 结论

1）刚度比大于0.42时，轨道梁、磁浮间隙的动力响应对刚度变化不敏感，系统横向动力学性能满足要求。

2）风致横向荷载会明显增大轨道梁的振动，并导致车体产生摆头运动，使端部磁浮间隙波动幅值增加，且列车尾部为导向电磁铁的最不利位置。

3）相较于轨道不平顺，风致横向荷载作用对系统横向振动的影响更为显著，应作为控制因素考虑。