基于赫兹公式的活性粉末混凝土间隙球铰静摩擦因数计算研究

曹锦承 刘来君 张杰 丁昊

长安大学公路学院，西安710043

转体施工法在跨越沟壑、峡谷等复杂地形条件下具有独特的优势［1］。球铰作为转体施工法中转体装置的重要组成部分，已成为当今国内外学者的研究热点之一。对球铰的精细研究，能够保证桥梁上部结构的转体施工质量，提高施工的安全性［2］。

国内外学者对转体球铰的研究主要集中在转体施工中的工作性能和应力分析方面。工作性能方面，文献［3］通过分析转体施工过程中不同环境因素，考虑其对转体装置球铰工作性能的影响。文献［4］针对转体球铰的结构特点并结合抗震要求，提出了一种新的连续梁转体系统。应力分析方面，学者大多研究普通球铰的力学性能。文献［5］通过考虑球铰的结构分析模型，推导了上球铰中心孔壁与销轴间距和上下球铰间摩擦板最小弹性压缩量的简化计算公式。文献［6］对比基于不同假设的转体施工中球铰应力计算方法的准确性，结合有限元分析提出计算方法的修正建议。文献［7］针对常规大吨位球铰提出了一种径向应力的计算方法。文献［8］针对桥梁平转过程，计算了球铰复杂状态下的主应力并得到该类桥梁所受正应力的强度条件。文献［9］对桥梁结构在偏载作用下的球铰性能进行分析，并验证了球铰的安全性。

现有相关理论在计算球铰转动时认为上下球铰全面积接触，这与实际情况不符。上下球铰接触面的接触面积与表面静摩擦因数是控制转体成功的主要因素，若对接触面上计算参数估算不准确，可能会出现牵引力不够，桥梁转不动的情况，也可能出现由于摩擦力不足，导致转动过程中转体结构倾覆。

本文基于赫兹公式和现有理论，提出修正球铰实际接触面积的球铰静摩擦因数计算方法，得到适用于间隙球铰的静摩擦因数计算公式，并通过一工程实例验证该公式的准确性。

1 称重试验及传统计算方法

1.1 球铰摩阻力矩测试原理

球铰称重试验时存在两种情况，须采用不同的称重计算原理。

1）当球铰的摩阻力距MZ小于桥梁结构的不平衡力矩MG时，转盘与承台之间的临时固结解除后，转体结构顺着不平衡力矩方向发生倾斜。假设下落端为主梁B端，则A端支反力P1为0，测量B端支反力P2；再顶升B端，使得桥梁结构倾斜方向改变，且保证A端支反力为0（图1）。记录转动过程中千斤顶和百分表读数，根据荷载-位移曲线判断克服最大静摩阻力矩时的力P3。此时转体不平衡力矩和球铰摩阻力矩分别为

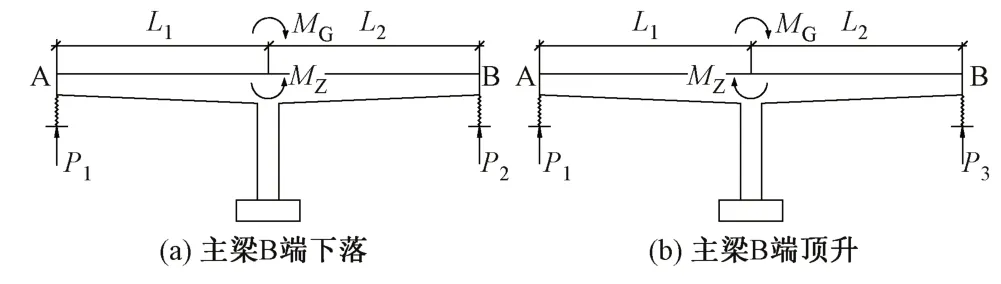
图1 球铰摩阻力矩小于转体不平衡力矩称重原理

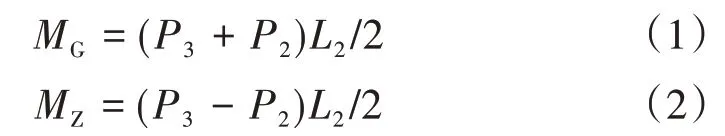
2）当球铰的摩阻力距MZ大于桥梁结构的不平衡力矩MG时，结构不会发生倾斜。分别在主梁A端，B端进行顶升，使结构在平面内发生顺时针、逆时针的微小转动，记录转动过程中千斤顶和百分百读数。根据荷载-位移曲线判断克服最大静摩阻力矩时的力P4和P5。此时转体不平衡力矩和球铰摩阻力矩分别为

图2 球铰摩阻力矩大于转体不平衡力矩称重原理

1.2 传统静摩擦因数计算方法

转动体球铰静摩擦因数传统方法［10］认为称重试验时转动体球铰在沿梁轴线的竖平面内发生微小角度的竖转。摩阻力矩为摩擦面每个微面积上的摩擦力对过球铰中心竖转法线的力矩之和。将球铰划分为许多微圆环，微圆环与球铰中线夹角为θ，球铰接触半径为c，设每一环的宽度为ds（图3）。图中，R为球铰的半径；μ0为球铰静摩擦因数；σ为球铰的转动质量在接触部分产生的压力分量。由图3的几何关系可知：dMZ=RcosθdF，dF=μ0σdA，dA=2πcds，c=Rsinθ，ds=Rdθ。其中，F为施加在球体上的法向力，A为微圆环面积。

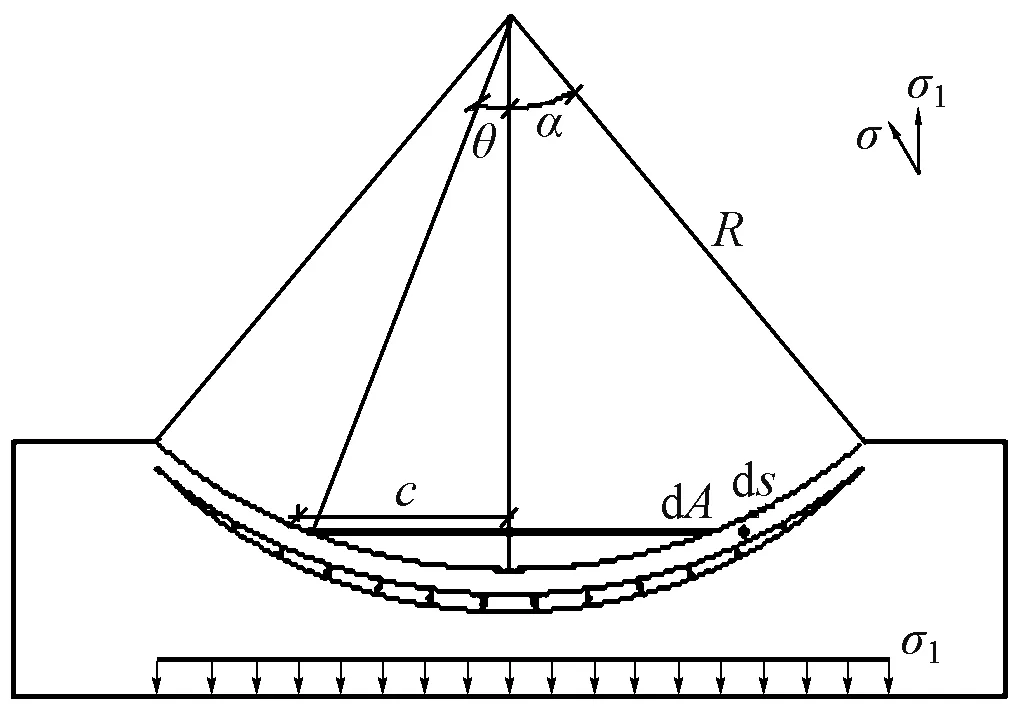
图3 传统方法转动体球铰静摩擦因数计算示意

根据图3得到MZ为

式中：N为转体质量。

传统理论认为当上球铰与下球铰半径相等时，上下球铰的接触面积相等，此时接触半径与球铰所划分的微圆环半径相等；若上下球铰半径不相等，式（5）则不再适用。实际工程中，上下球铰具有不相等的情况，因而需要推导出一种适用于上下球铰半径不相等的静摩擦因数计算方法，即上下球铰自一开始接触就存在间隙，本文称为间隙球铰。

2 修正接触面积的计算方法

赫兹公式［11］认为当两球体接触时，其接触区域为一个圆面，接触半径c为

导数作为函数在某一点处的瞬时变化率刻画了函数变化趋势(上升或下降的陡峭程度)，而函数的单调性也是对函数变化趋势的一种刻画，那么导数与函数的单调性有什么联系呢？(教师通过用超级画板演示曲线上点在运动的过程中，提醒学生注意观察切线的斜率符号的变化.)

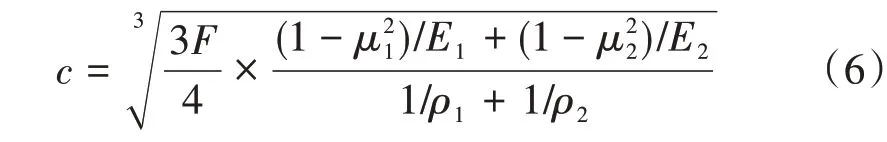
式中：μ1、μ2分别为两球体的泊松比；ρ1、ρ2分别为两球体的曲率半径；E1、E2分别为两球体的弹性模量。

接触面积变化时，竖向压力也发生变化。修正面积法转体间隙球铰静摩擦因数计算示意如图4。可见，当上下球铰半径不相同时球铰边会产生接触间隙，传统计算公式已不再适用。

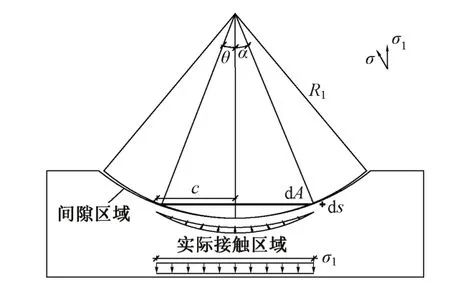
图4 修正面积法转体间隙球铰静摩擦因数计算示意

考虑接触压力与接触区域内任意一点到接触中心的距离成正比［12］，结合球体变形分析，确定接触压力分布函数为

式中：σ(ρ)为接触区域内任意一点的接触压力；σmax为接触面上最大接触压力；ρ为接触区域各圆环半径；φ为竖直方向和每个圆环形成的夹角；ρsinφ为接触区域内任意一点到接触中心的距离。

考虑接触压力分布的对称性，以ρ为半径的同一圆环接触区域内，接触压力相等。因此，只需要知道圆环上的一点，即可确定环中其余部分的接触压力。根据几何关系式（7）简化为

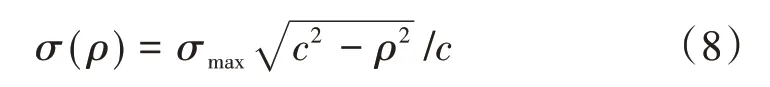
根据图4的几何关系，将简化公式的参数与球铰中的几何参数相对应，可得

考虑间隙的存在，积分上限需要按照接触半径进行修改，根据图4几何关系可知：

式中：R1、R2分别为上球铰和下球铰球体半径，对于转体施工桥梁球铰，R1取正值，R2取负值，k1、k2均为与材料泊松比以及弹性模量有关的常数。

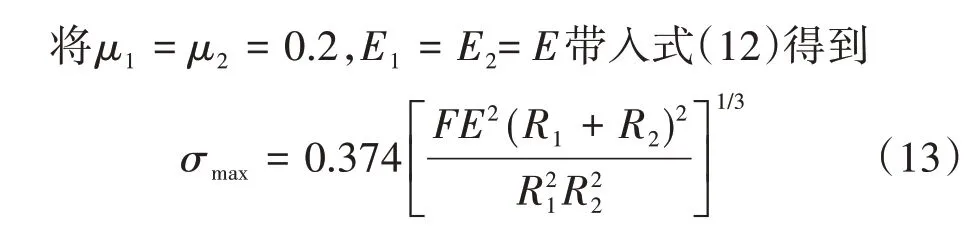
式中：E为接触材料的弹性模量，即上下球铰的材料弹性模量。

实际工程中，球铰材料等参数可确定，由式（6）求得接触半径，再代入式（11）得到静摩擦因数为

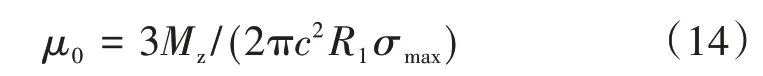
由于接触面积的改变，转体牵引力的计算方法已不再适用。文献［12］发现采用平面积分法计算时须假定撑脚与滑道、上下球铰均为全面积接触，忽略因滑片布置不当引起的接触空隙，但这类算法不适用间隙球铰。计算间隙球铰牵引力时，本文认为转体过程中撑脚悬空，接触区域为赫兹公式的接触圆区域，实际接触面可视为由无数部分微圆环积分而成，部分圆环可以简化为一小矩形微元（图5），微元面为rdβdr，其所受压力力臂为r。

图5 平面积分微圆

积分推导出球铰处摩擦力M1为

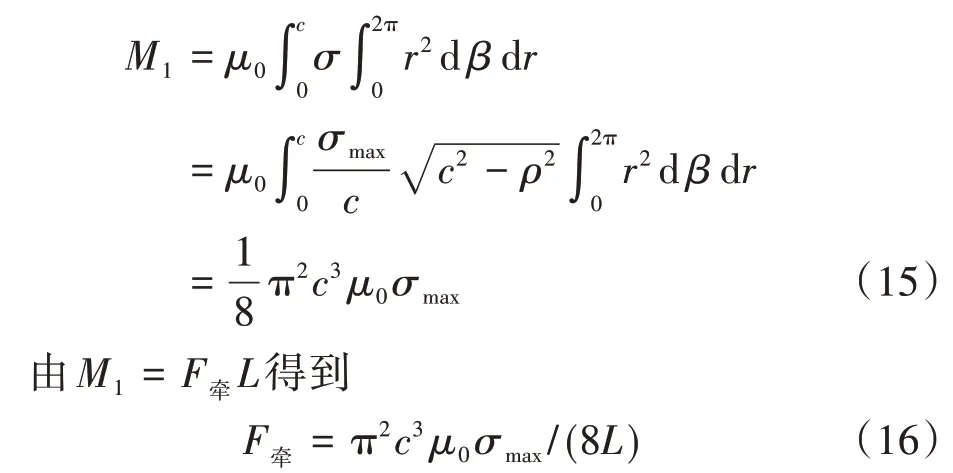
式中：L为牵引力力臂。

3 工程算例

依托国道108线禹门黄河桥西引桥转体工程，14#，15#墩转体质量分别为11 020.2，8 485.8 t。转体球铰采用活性粉末混凝土（Reactive Powder Concrete，RPC）组合球铰，见图6。14#、15#墩球铰实际承重分别为13 000，10 000 t。上下球铰的接触表面为钢表面。

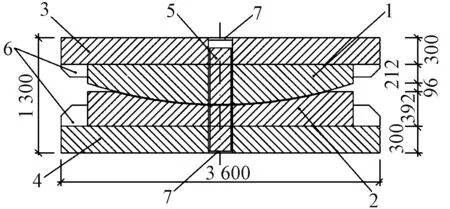
图6 工程用RPC球铰（单位：mm）

由于球铰上下盘为钢混复合材料，考虑RPC与钢材的弹性模量不同，参考文献［13］中Voigt和Reuss等应变模型推导的两相复合材料等效弹性模量，则

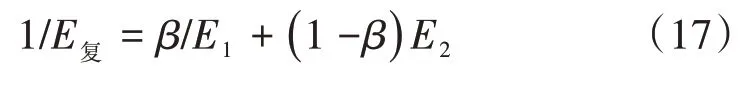
式中：E复为球铰的复合弹性模量；β为两种不同材料等应变模型体积所占比例。

以15#墩RPC组合球铰为例，球铰采用C120级RPC材料，弹性模量为42 MPa，泊松比0.2；接触面钢材采用Q235钢材，弹性模量为200 GPa，泊松比0.24；上球铰半径4.800 m，下球铰半径4.929 m，上球铰平面直径3.0 m，下球铰平面直径2.4 m，千斤顶距离球铰中心L=L1=L2=4.35 m。

根据球铰称重试验（图7）可知，该试验属于1.1节中第二种情况，测得P4=969.51 kN，P5=2 130.03 kN。将其代入式（3）和式（4）可得转体不平衡力矩MG=2 524.13 kN·m，RPC组合球铰摩阻力矩MZ=6 741.50 kN·m。

图7 试验现场

参考赫兹公式，利用式（4）计算得到15#墩的接触半径为4.6 m。对比传统计算法与修正面积法计算的静摩擦因数并反算牵引力，再将其与实测牵引力对比，结果见表1。

表1 传统方法与修正方法计算值与实测数据对比

由表1可知，对于RPC间隙球铰，传统计算法牵引力计算值远大于实测值，误差达到了43.5%，修正面积法牵引力计算值略大于实测值，误差为9.4%，控制误差在10%以内，且不失一般性，该方法可以运用到实际工程间隙球铰中。

4 结论

1）传统的计算方法认为上下球铰为紧密接触状态，球铰之间不存在接触间隙，只适用于一般球铰，针对于间隙球铰，牵引力计算值与实测值存在较大误差，已不再适用。

2）基于赫兹公式对有效接触面积修正的方法，可计算间隙球铰的静摩擦因数，与实际工程较为吻合，广泛适用于上下半径不同的间隙球铰中。