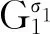构造等斜能量定向图的两种方法

赵炳荧，冀孟达，王 盟

(西北工业大学数学与统计学院，西安 710129)

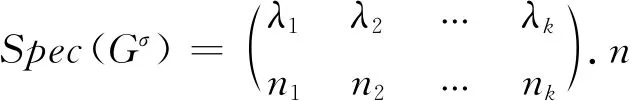
图谱理论是代数图论的一个重要研究课题，而图的能量则是图谱理论的重要研究内容.图G的能量是指图G的邻接矩阵特征值的绝对值之和.1978年Gutman首次给出了图的能量的概念[1]，从此图能量的相关研究受到了国内外学者的普遍关注，取得了大量的图能量的研究成果[1-4].2010年，Adiga等[5]首次给出了定向图斜能量的概念，文献[10-11]分别研究了竞赛图和定向图斜能量的一些性质，文献[12-13]分别研究了竞赛图斜能量的下界和定向图斜能量关于斜秩和最大度的上界.文献[6]中Li和Lian提出问题“如何构造一些具有不同斜谱但等斜能量的定向图类”.在文献[14]中Ramane等人利用两个定向图的联图构造了具有不同斜谱但等斜能量的定向图类.Adiga等[15]给出了一些新的方法构造了等斜能量的定向图类.刘香香等[16]通过将无向图上的顶点冠和邻接冠推广到定向图上，构造等斜能量定向图.本文推广定义了定向图的广义顶点冠和广义邻接冠，得到了相应的斜谱，并在此基础上构造了新的具有不同斜谱但等斜能量的定向图类.

1 一些定义与引理

这一节推广了文献[16]的定向图的顶点冠和邻接冠的定义，并给出了一些有用的引理.

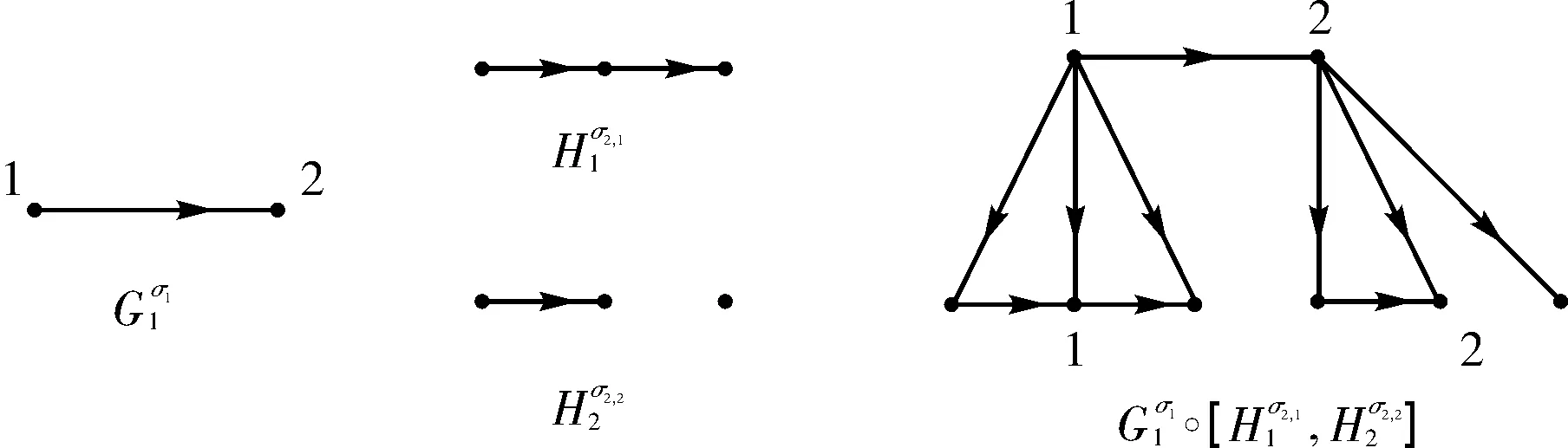
图1 定向图和广义顶点冠Fig.1 The oriented graphs and

图2 定向图和广义邻接冠★Fig.2 The oriented graphs and the generalized neighborhood corona ★

定义5[18]矩阵A∈Cm×n和B∈Cp×q的直积用A⊗B表示，具体如下所示：

引理1[17]设M、N、P、Q为矩阵，若其中M为可逆矩阵，则

若其中Q为可逆矩阵，则

引理2[18]矩阵A∈Cn×n，则矩阵A是正规矩阵的充分必要条件是，存在酉矩阵Q，使得A酉相似于一个对角阵，即

其中,λ1，λ2，…，λn是A的特征值.

2 主要结果及证明

本节给出了定向图广义顶点冠和广义邻接冠的斜谱，在此基础上，给出了两种构造具有不同斜谱但等斜能量的定向图类的方法.

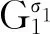
其中,i=1，2，…，n，j=2，3，…，m，k=1，2，…，n.

证明根据广义顶点冠的定义，Gσ的斜邻接矩阵如下：

其中,

e为m维全为1的列向量.

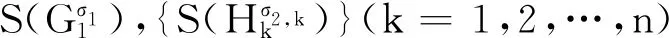
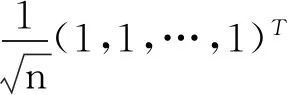
其中e1=(1，0，0，…，0)T为m维列向量，

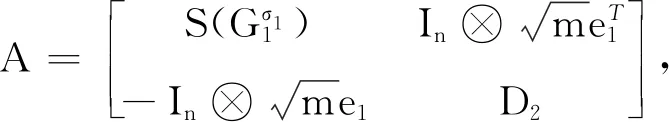
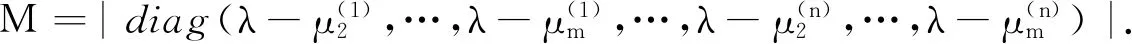
则

综上所述，定向图Gσ的斜谱如下：

其中,i=1，2，…，n;j=2，3，…，m;k=1，2，…，n.

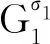
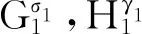
并且根据定理1它们的斜谱不同.

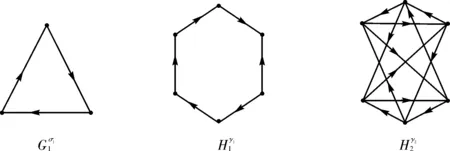
图3 定向图和Fig.3 The oriented graphs

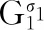
其中，i=1，2，…，n;j=2，3，…，m;k=1，2，…，n.

证明根据广义邻接冠的定义，Gσ的斜邻接矩阵如下：

其中，

e为m维全为1的列向量.

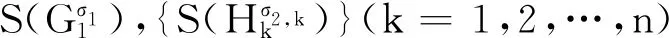
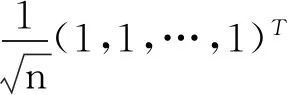
其中，e1=(1，0，0，…，0)T为m维列向量，

记

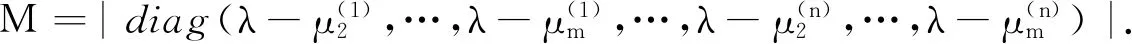
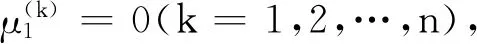
综上所述，Gσ的斜谱如下：

其中,i=1，2，…，n;j=2，3，…，m;k=1，2，…，n.

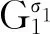
证明根据定理3可以得到Gσ的斜谱，再根据斜能量的定义，该定理得证.