感应电机低复杂度三矢量预测电流控制

(广西大学 电气工程学院， 广西 南宁 530004)

0 引言

感应电机(induction motor, IM)具有结构简单、价格低廉、可靠性高等特点，在电气拖动系统中广获关注与应用。模型预测控制(model predictive control, MPC)是近年来继磁场定向控制(field oriented control, FOC)和直接转矩控制(direct torque control, DTC)后在电力电子与电气传动领域蓬勃发展的一种先进控制策略[1]。与FOC和DTC相比，MPC采用非线性控制策略对变流器进行控制，取代了FOC中的电流PI内环控制和调制模块，在转矩响应速度、电流畸变及转矩纹波等性能指标上更优于FOC；MPC采用代价函数代替DTC开关表，最佳电压矢量选择的方式更准确高效，能获得更好的稳态性能[2]。

模型预测电流控制(model predictive current control, MPCC)和模型预测转矩控制(model predictive torque control, MPTC)是MPC应用最广泛的两种方法[3]。传统MPTC代价函数包含转矩和磁链两种不同量纲的变量，因此需要考虑加权因子的设计问题，而MPCC的代价函数只包含电流一个控制变量，无需使用加权因子，算法更简单[4-5]。传统MPCC针对所有可行的电压矢量预测定子电流，通过代价函数进行评估，从而选出令代价函数最小的电压矢量作用于逆变器，这种方式需要进行多次预测和比较计算，对软、硬件设备性能要求较高，实际应用受限。常见的改进方法是在预测前先对备选电压矢量集进行优化筛选，避免对全部电压矢量进行滚动优化[6- 8]，文献[9-10]利用零矢量作用时的电流误差，减少预测次数，计算量降低，但每个周期只作用一个电压矢量，稳态性能有待改进。

传统单矢量MPCC在稳态性能方面无法达到最优效果，针对这一问题的解决方案可分为两大类：多矢量调制和扩展电压矢量控制集。文献[11-14]采用多矢量策略，其中文献[11]采用双矢量MPCC，最优非零矢量通过识别定位参考电压矢量的扇区获得，无需进行6次代价函数比较，减小计算量的同时提高了稳态性能。文献[12-13]提出三矢量MPCC，文献[12]在每个扇区中利用3个基本电压矢量合成一个方向和大小均可变的虚拟电压矢量，并将六个扇区总共合成的6个虚拟电压矢量作为备选矢量集，但仍需进行6次预测比较，文献[13]首先利用代价函数最小化选出第1个非零矢量，然后根据第1非零矢量作用下的电流误差位置选择第2非零矢量，再引入零矢量进行最优矢量合成，三矢量策略能有效减小稳态转矩磁链脉动和电流谐波，但计算复杂的问题仍需解决。文献[14]采用占空比调制，同时将扇区重新划分为3个，电流预测迭代次数减少为3次，稳态改善效果明显。文献[15]将原有的6个基本有效矢量幅值减少一半，方向固定不变，同时将相邻两个有效矢量合成为新的电压矢量，以此构建扩展矢量集，但稳态提升效果有限。

为了在提高MPCC稳态性能的同时降低计算复杂度，以感应电机为控制对象，提出一种低复杂度三矢量模型预测电流控制方法(low-complexity three-vector model predictive current control, LC-3VMPCC)，通过评估零矢量作用时的电流误差矢量的位置，仅1次预测就能快速锁定最佳矢量位置，然后在一个周期内同时作用三个基本电压矢量，根据最小化电流误差的原则能有效快速地获得基本矢量的作用时间，省去复杂的电流斜率计算过程。该方法计算复杂度低，不仅具有传统MPCC的快速动态响应，同时还改善了控制的稳态性能，最后通过基于dSPACE的两电平-三相逆变器供电的感应电机驱动平台进行实验，结果验证所提方法的正确性和有效性。

1 感应电机数学模型

在α-β坐标系下，以定子磁链ψs和定子电流is为状态变量的感应电机数学模型为

(1)

(2)

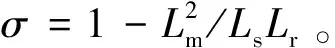
对式(1)采用前向欧拉离散法，得到定子电流is的预测模型为

(3)

式中，is(k+1)为下一时刻定子电流预测值;is(k)为当前时刻定子电流测量值;ψr(k)为当前时刻转子磁链值;us(k)为当前时刻作用的电压矢量;ω(k)为当前时刻的转子转速;Ts为采样时间;Rσ=Rs+kr2Rr;τσ=Lσ/Rσ;Lσ=σLs;τr=Lr/Rr;kr=Lm/Lr。

2 传统模型预测电流控制

传统的感应电机模型预测电流控制主要包括：转速和磁链外环PI调节、定子电流内环预测、磁链观测、以及代价函数最优化。开关状态与电压矢量关系见表1，两电平-三相电压源型逆变器共有8个基本电压矢量，8组开关状态。传统单矢量MPCC将定子电流作为控制目标，将8个基本电压矢量分别代入式(3)得到相应电流预测值，再代入式(4)，通过滚动优化选出能最小化代价函数J的电压矢量，并将相应的开关状态发送至逆变器。

J=|is*-is(k+1)|,

(4)

式中，is*为α-β静止坐标系中的定子电流给定值。

表1 开关状态与电压矢量Tab.1 Switching states and voltage vectors

3 低复杂度三矢量预测电流控制

3.1 矢量组合选择

传统单矢量MPCC需要进行8次预测和排序，计算负担大。为了简化算法，当一个周期内只作用零矢量时的电流预测值为

(5)

将式(5)代入式(3)可以得到

(6)

式中，usv表示非零电压矢量，v=1，2…，6。因此，在每个控制周期结束时由usv引起的预测电流与参考电流之间的误差为

(7)

式中，Δis0(k+1)为零矢量单独作用时引起的电流误差。为了便于说明LC-3VMPCC的原理，定义如下三个矢量：

(8)

n=Δis0(k+1)，

(9)

g=Δisv(k+1)，

(10)

式中，|g|=|Δisv(k+1)|=|is*-is(k+1)|，为预测电流控制的代价函数(4)，因此当|g|最小时，电流误差可达到最小值。式(7)可以重新表示为

n=m+g。

(11)

图1 单矢量LC-MPCCFig.1 One vector based LC-MPCC

以第Ⅰ扇区(-π/6～π/6)为例，当n(即零矢量作用时引起的电流误差)位于第Ⅰ扇区时，三个矢量在空间上的关系如图1所示。m1、m2和m6分别为电压矢量u1、u2和u6作用时间为Ts时引起的变化矢量，g1、g2和g6分别为对应的电流误差矢量，可以看出，最靠近n的矢量m1可获得最小电流误差，即g1，故选择的非零电压矢量为u1。

从图1可以看出，当只单独作用一个基本电压矢量时，定子电流误差幅值|g|相对较大。因此，为了进一步减小电流误差，实现电流无误差控制，提出一种低复杂度三矢量模型预测电流控制，在每个控制周期内同时作用两个非零电压矢量和一个零矢量，在理论上能实现电流的无差跟踪。

LC-3VMPCC的控制框图如图2所示，首先根据Δis0(k+1)确定最优矢量所处的扇区位置，然后确定最优矢量组合，再根据矢量在空间上的几何关系分别计算各电压矢量作用时间，合成新的理想电压矢量并通过脉冲发生器将开关信号输送至逆变器，进而控制感应电机。

LC-3VMPCC的实现原理如图3所示。重新划分扇区，以n位于扇区Ⅰ(0～π/3)为例，选择构成扇区Ⅰ边界的u1和u2作为非零电压矢量，当u1和u2作用时间分别为T1和T2时，得到矢量m1与m2，如图3(a)所示，当g的幅值不为0时，意味着电流误差存在，为了在理论上实现电流无误差控制，u1和u2的合成矢量需精确跟踪n，使g的幅值强制为0，如图3(b)所示，则满足以下关系：

n=m1+m2。

(12)

根据上述分析可知，此时代价函数的最小值为0，因此在LC-3VMPCC策略中，理论上能消除周期结束时的电流误差，从而减小电流和转矩脉动，所有扇区的矢量组合见表2。

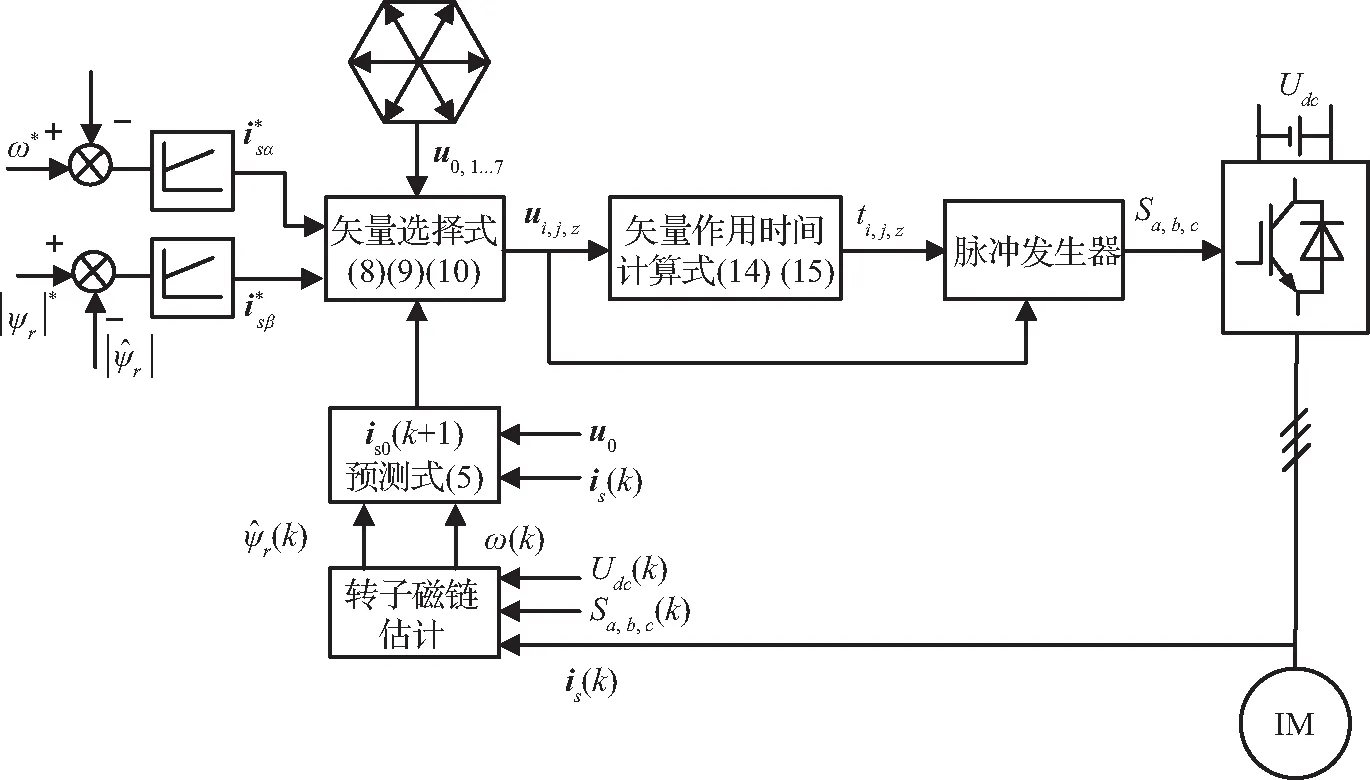
图2 LC-3VMPCC控制框图Fig.2 Block diagram of LC-3VMPCC

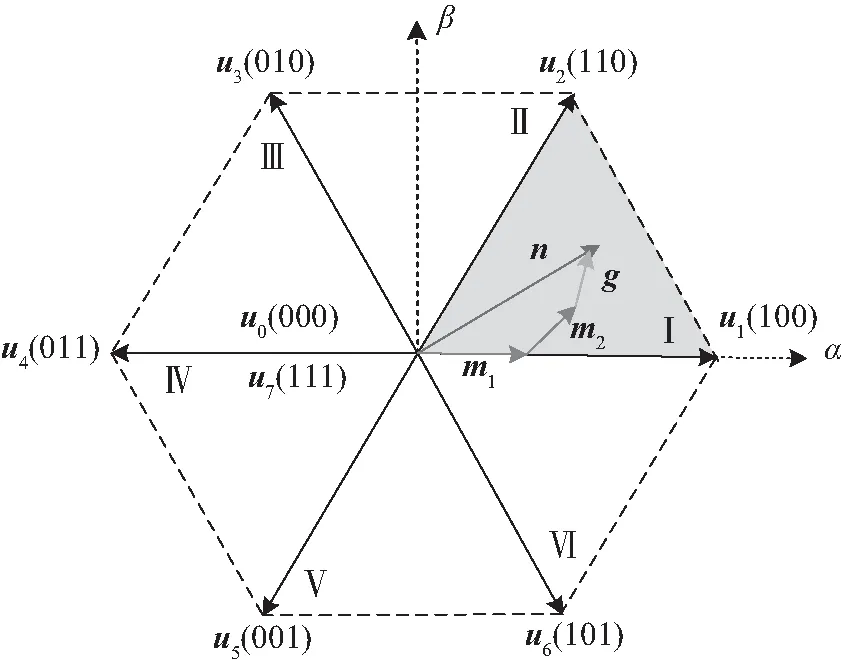
(a) g不为0

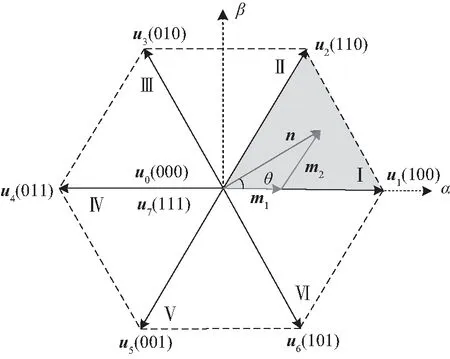
(b) g为0

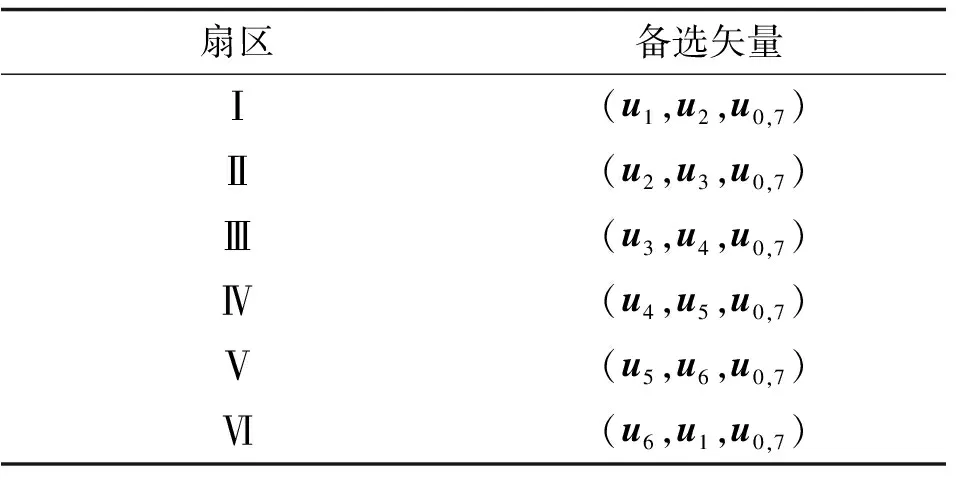
表2 矢量组合Tab.2 Vector group

3.2 电压矢量作用时间

理想电压矢量的合成需要2个因素，一是电压矢量组合，二是各电压矢量的作用时间。根据如图3所示几何关系，采用正弦定理可得到以下关系：

(13)

式中，m1=T1|u1|/τσRσ，m2=T2|u2|/τσRσ。由式(13)可得u1、u2和u0作用时间T1、T2和T0分别为

(14)

当T1+T2>Ts时，对T1和T2作如下修正：

(15)

因此，合成的理想电压矢量为us*=T1/Tsu1+T2/Tsu2+T0/Tsu0。采用文献[16]的方法，选择u0作为零矢量，六个不同扇区的矢量作用序列见表3。

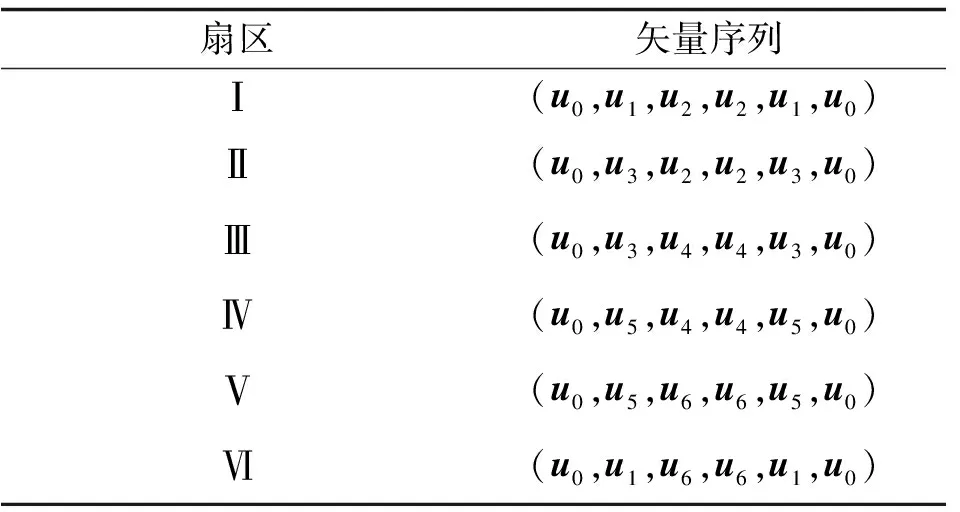
表3 矢量序列Tab.3 Vector sequence

3.3 算法流程与分析

低复杂度三矢量MPCC算法具体流程如下：

① 变量测量与估计：采样当前k时刻的电流值is(k)，直流侧电压值Udc(k)和转速ω(k)并观测出当前时刻的转子磁链ψr(k)。

② 变量预测：根据式(5)预测k+1时刻零矢量单独作用时的电流值is0(k+1)。

③ 矢量选择：根据式(8)、式(9)和式(10)及表2进行最优三矢量组合选择。

④ 作用时间计算：根据式(14)计算出各个电压矢量的作用时间，并由式(15)进行约束校正。

⑤ 根据上述所得的电压矢量组合和作用时间合成理想电压矢量，经过脉冲发生器发出相应脉冲并输至逆变器。

与传统基于单矢量的MPCC方法相比，LC-3VMPCC在理论上可以保证代价函数最小，并消除每个控制周期结束时的电流误差，因此它可以有效抑制电流谐波和转矩脉动，在理论上实现电流的无误差控制。与现有三矢量策略相比，LC-3VMPCC直接确定最优矢量组合，无需进行多次预测和代价函数滚动比较，大大减小计算量，降低了对控制器计算能力的要求，具有很大的工程应用前景。

4 试验结果分析

为验证所提方法的正确性和有效性，在基于dSPACE1104的两电平-三相逆变器供电的感应电机驱动平台上进行试验，试验平台如图4所示，试验电机参数见表4。试验系统的采样频率为8 kHz，死区时间为4 μs。

图4 试验平台Fig.4 Experimental platform

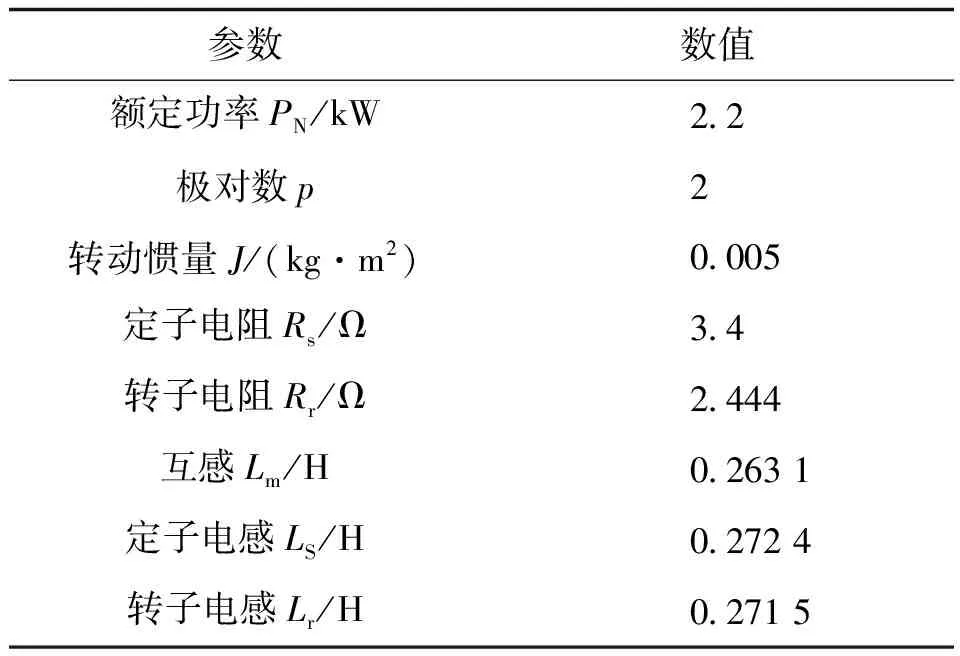
表4 380 V, 50 Hz感应电机参数Tab.4 380 V, 50 Hz IM Parameters

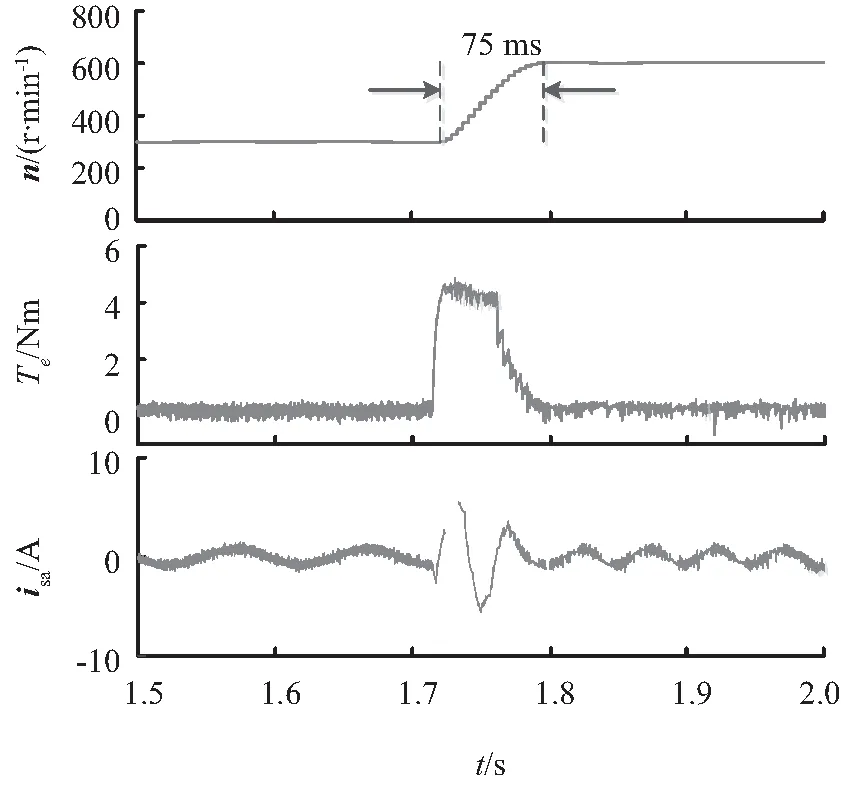
首先，对传统单矢量MPCC和LC-3VMPCC两种策略进行转速加速阶跃变化试验对比，试验结果如图5所示。试验电机空载起动，给定转速从300 r/min突增至600 r/min，可以看到，传统单矢量MPCC大约经过75 ms上升至给定速度，LC-3VMPCC则大约经过77 ms，两种策略的响应速度相当，均能较准确快速地跟随给定转速的变化，LC-3VMPCC能保持与传统MPCC策略相似的良好动态性能。

(a) 传统单矢量

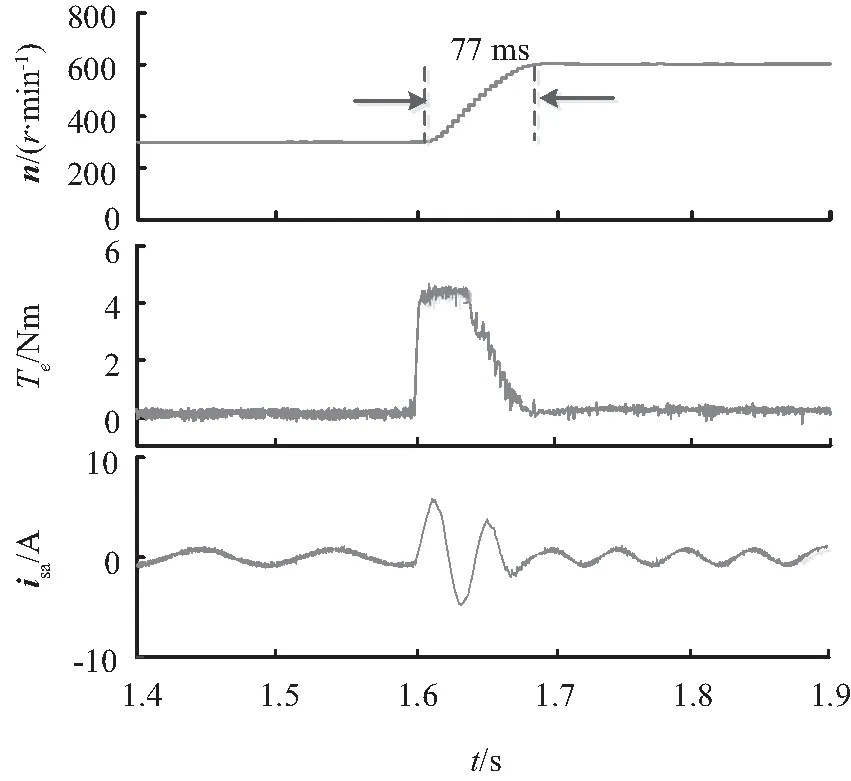
(b) 低复杂度三矢量

图6为两种策略突增、突减负载的试验波形。电机给定转速保持300 r/min，负载转矩首先由0.5 Nm突增至5 Nm，待电机运行稳定后，再从5 Nm突减至0.5 Nm。可以看出，两种策略在负载突变时，转速发生小幅度波动，但稳定后转子转速能恢复到原来的参考转速，在两种方法中可以观察到相似的负载转矩动态响应，但LC-3VMPCC负载上升过程比较平稳，表现出比传统单矢量MPCC更好的稳态性能，转矩脉动和电流谐波也都得到了明显改善，验证了上文的理论分析。

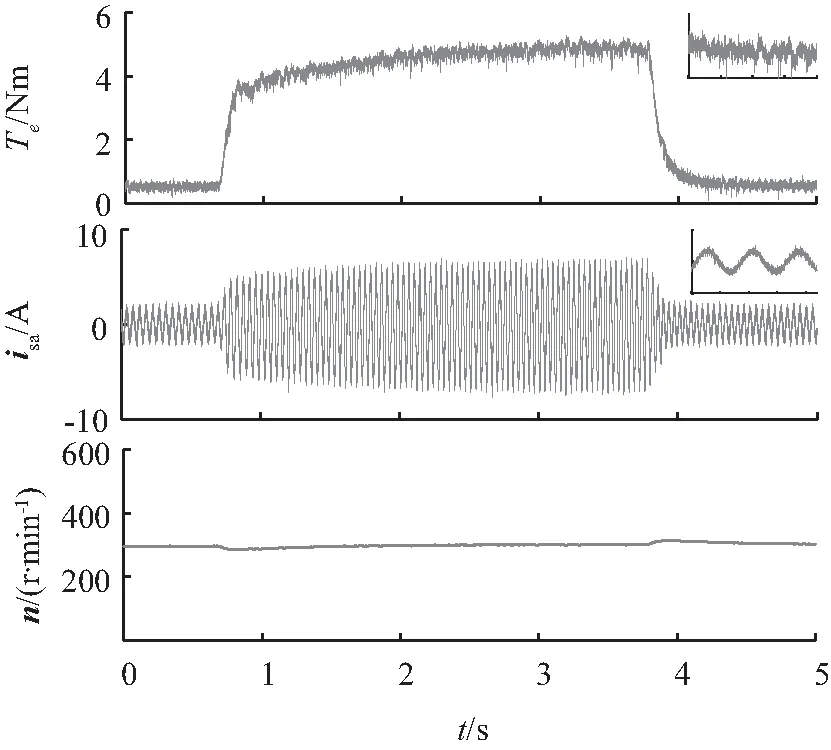
(a) 传统单矢量

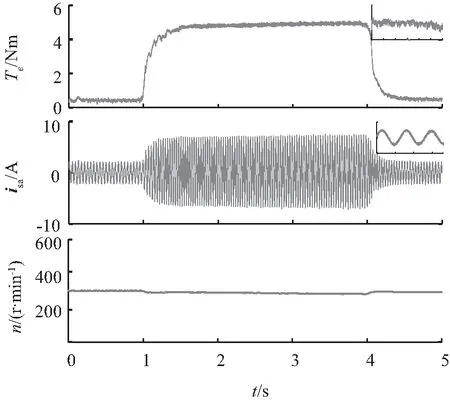
(b) 低复杂度三矢量

为了直观体现出LC-3VMPCC优良的稳态性能，截取0～0.3 s电机运行于200 r/min空载稳态时的局部A相定子电流进行谐波分析，结果如图7所示。传统单矢量MPCC的谐波总含量为36.69%，而LC-3VMPCC的THD仅为10.93%，谐波总量降低约3.4倍，LC-3VMPCC具有更良好的稳态效果，为了更进一步提高说服力，在6种由低到高的不同转速下对A相电流进行傅里叶分析(FFT analysis)，分析结果如图8所示，可以看出在任何转速下，LC-3VMPCC的THD总比传统单矢量MPCC低。

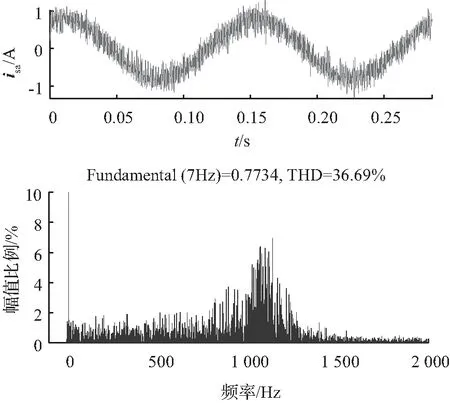
(a) 传统单矢量

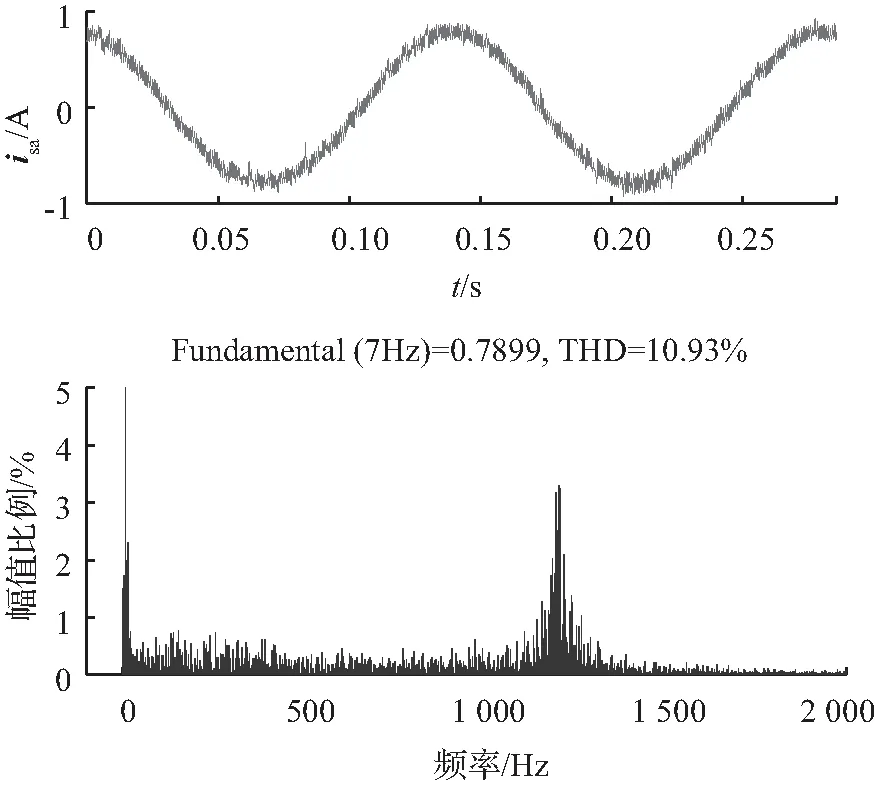
(b) 低复杂度三矢量

图9为两种控制策略在不同转速下，电机空载运行时的稳态电磁转矩脉动Te_ripple对比，为了定量分析比较，实验采集10 000组数据，根据转矩脉动公式(16)进行计算。

(16)

图8 不同转速下A相电流谐波分析Fig.8 Harmonic analysis of phase A current at different speeds

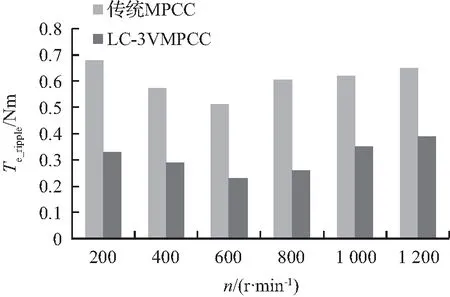
图9 不同转速下的转矩脉动对比Fig.9 Comparison of torque ripple at different speeds

5 结论

本文以降低传统MPCC策略的算法复杂度和提高控制的稳态效果为目标，提出一种低复杂度三矢量MPCC方法。该方法根据零矢量单独作用时的电流误差快速定位最优电压矢量的扇区位置，减少了电流预测和电压矢量枚举比较次数，采用三矢量合成幅值和方向均可调节的理想电压矢量，根据几何关系计算各个电压矢量作用时间，简单快捷，易于应用。实验结果表明，在较宽的速度范围内，所提方法具有与传统策略类似的优良动态响应能力，在稳态时，所提方法的电流谐波和转矩脉动大大降低，控制的稳态精度得到明显的提高。