基于LSTM和声发射的金刚石砂轮磨损状态识别*

苏史博,毕 果,郑守红,刘 杉

(厦门大学航空航天学院，福建 厦门 361102)

0 引言

在光学元件的超精密磨削加工中，砂轮磨损状态关乎砂轮的磨削性能，影响加工精度和加工效率。为了保证元件的正常加工，需要及时地更换修整磨损过度的砂轮。而在车间的生产过程中，由于无法准确地判断砂轮的磨损状态，只能凭借经验将剩余寿命还有较大余量的砂轮替换修整。另一方面，加工过程中的各种突发因素都可能使砂轮磨损状态发生意外突变。因此，在线准确识别砂轮的磨损状态从而判断是否需要修整，既能够保证加工的精度和安全，又能充分利用砂轮的使用寿命，具有较大的经济价值。

磨削加工过程中砂轮与加工材料的相互作用使材料发生形变时会产生大量的弹性应力波，这就是声发射现象。自从上世纪五十年代Kaiser首次发现声发射现象[1]以来，声发射被广泛应用到很多监测和诊断上的诸多领域。伯克利大学较早地将声发射运用于砂轮磨损状态监测[2]，Mokbel A A等发现砂轮的磨损会造成声发射信号幅值的提升[3]。

但是上述方法常常依赖于各种精巧的阈值设置和时域特征选择，实际应用和推广困难，基于数据驱动的诊断方法受到了更多的关注。Ghosh N等开发了基于神经网络的刀具状态监测传感器融合模型[4]；刘然结合前馈神经网络(Back Propagation Neural Network, BPNN)和自回归移动平均模型(Autoregression and moving average, ARMA)构建了刀具磨损量评估模型[5]。砂轮磨损是一个历经初期磨损、稳定磨损、急剧磨损三个阶段的缓慢变化过程，从声发射样本预测砂轮的磨损状态本质上是一个时间相关序列的模式识别问题。传统BP神经网络处理时间相关序列上存在较大的局限性。循环神经网络(Recurrent neural network，RNN)是一种用于时序列识别的模型，但在砂轮磨损状态识别问题上却较少有研究。传统RNN难以实现对长时间依赖的建模[6-7]，不适用于从缓慢变化到急剧变化的砂轮磨损过程。Hochreiter S等提出长短时记忆模型(LSTM)，将隐含层的节点替换为一个特殊的复合存储单元，获得建模长时间依赖序列的能力[9]。

针对砂轮磨损状态识别的问题，本文建立了一个长短时记忆(LSTM)循环神经网络模型，通过小波包能量系数法获取砂轮磨损的敏感频段特征，并使用主成分分析对特征进行降维，使用长短时记忆网络识别砂轮的磨损状态。在实验的基础上，通过与频域分析、BP神经网络的对比，证明LSTM构建的网络具有识别精度高、收敛速度快、离群值较少等优点，验证了方法的有效性。

1 理论基础

1.1 LSTM循环神经网络模型

为了克服传统BPNN神经网络在处理时间相关序列上的局限性，循环神经网络(RNN)在不同层间节点连接的基础上添加了隐含层节点与节点间的连接，使得网络保留了过往输入节点的信息，从而获得了建模时间相关序列的能力[7]，其网络结构如图1所示。砂轮声发射信息样本随时间的变化中蕴含着识别砂轮磨损状态的必要特征，在稳定磨损阶段砂轮磨损状态变化较为平缓，声发射信号相邻帧之间的差异较小；而当砂轮处于急剧磨损阶段时，磨损状态变化剧烈，声发射信号相邻帧之间的差异较大[10]。上述过程是一个缓慢变化的过程，这就要求识别模型具备建模长时间依赖的能力。RNN由于其网络特点，如果节点循环边的权重小于1，那么第一个时间步的输入对最后一个时间步的输出的贡献将会随时间间隔而指数衰减，如图2所示，这就限制了网络建模长距离时间依赖的能力。长短时记忆模型LSTM将隐含层的节点替换为一个特殊的复合存储单元。这个特殊单元通过选择性地保留或丢弃过往时间节点的输入，从而获得建模长时间依赖序列的能力，更适合用来建模砂轮的磨损过程。

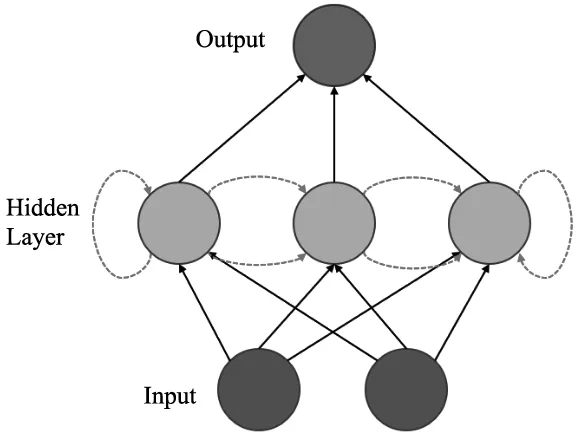
图1 RNN网络结构图

图2 RNN网络梯度消失可视化

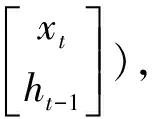
(1)

本时刻单元的状态ct计算表达式如式(2)～式(4)所示，其中Wi为输入权重矩阵，Wc为状态权重矩阵。

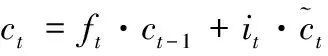
(2)

(3)

(4)

本时刻单元输出ht的计算表达式如式(5)、式(6)所示，其中Wo为输出权重矩阵。

ht=ot·tanh(ct)

(5)

(6)

图3 LSTM单元基本结构

1.2 敏感频段分析及特征降维

对模型而言输入特征对模型精度和运算速度等尤为重要，本文使用小波包分析获取声发射信号各个频段的能量系数，并计算各频段能量系数随砂轮磨损状态的变化程度以确定砂轮磨损的敏感频段，从而提取用于训练网络的频域特征。

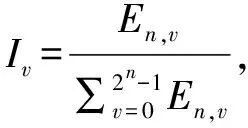
虽然小波包分析确定了声发射信号对于砂轮磨损的敏感频段，但是对应频段的频域特征数量还是很大，存在较大数量的冗余特征。如果直接将对应频段的频域特征作为神经网络的输入节点，会造成网络规模和层数过大，对网络的训练和部署造成不必要的麻烦。因此本文使用主成分分析(PCA)对敏感频段频域特征进行降维，设定累计贡献率为95%，将特征维度降为15维。

2 实验与验证

2.1 实验

本文以厦门大学研发的三轴超精密成型磨床为基础实验平台，金刚石砂轮安装于机床主轴，磨削加工材料为熔融石英。声发射传感器通过耦合剂与工作台接触，熔石英玻璃置于工作台上，四周由吸附于工作台上的挡铁固定。声发射信号采集系统使用美国物理声学所生产的PCI-2高性能声发射采集卡，采样频率为1 MHz。如图4所示。

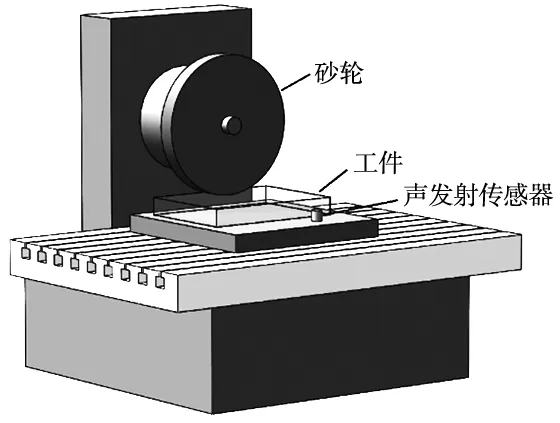
图4 砂轮全寿命磨削实验平台

使用刚修正过的砂轮进行磨削实验，实验中根据材料去除量设置不同的观测节点，采集声发射信号和砂轮表面形貌，如图5所示。考虑到砂轮初期变化较为显著，第1个节点对应的材料去除量为4 cm3，之后以20 cm3为间隔设置采集节点，当完成第16个节点采集后，工件表面出现明显损坏，停止实验。主要实验参数如表1所示。

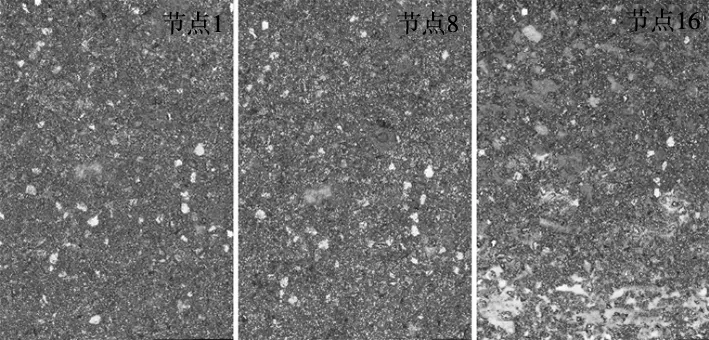
图5 砂轮表面显微形貌图

表1 磨削加工参数

2.2 数据分析和特征提取

为便于分析数据的时频域特征，将声发射信号进行分帧处理，每帧时长为10 ms，帧间没有重叠，对应的采样点数为10 000点，从而构建一个砂轮磨削声发射信号数据集。

把采集到的第1节点的数据和第16个节点的数据分别做频域分析，如图6所示。从图6上可以看出，声发射信号时域信号随机性很强无法分辨，而频域上频带很宽，分布随机。从频带内虽然可以看出频率信息发生了变化，但很难从频率域上准确识别砂轮的磨损状态信息。

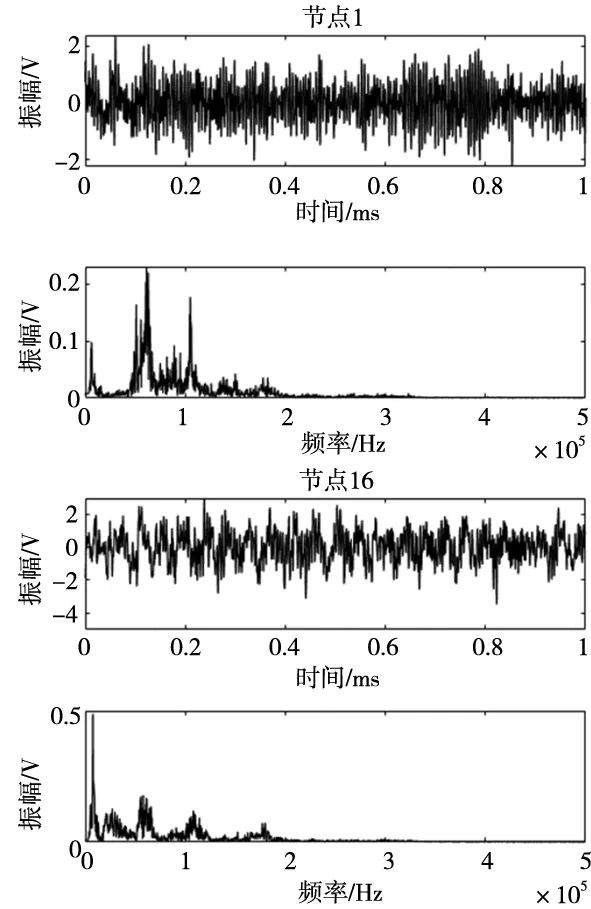
图6 声发射信号频域分析

对实验采集到的声发射信号进行小波包分析。对采样频率为1 MHz的声发射信号进行4次分解，将信号的频带等分为0～500 kHz的16个部分。计算各频段内小波包能量系数的方差，如图7所示，可以看出，低频段内小波能量系数的方差最大，说明此频段为砂轮磨损状态变化的敏感频段，因此将低频段的500个特征作为模型的输入。

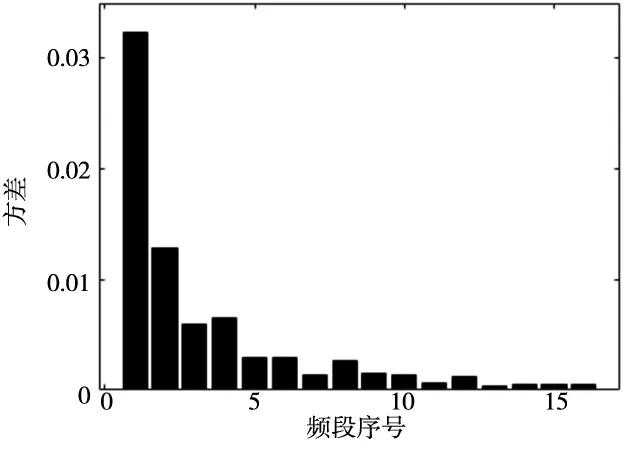
图7 小波能量系数方差

对低频段的特征使用主成分分析进行降维得到15维特征，作为神经网络的输入。为了验证神经网络是否能从声发射信号的降维特征信息中获取到砂轮的状态，将处于初期磨损的第1组样本标记为0，而将已经严重磨损的第16组样本标记为1，以降维得到的15维特征为输入，对3层的LSTM网络进行简单二分类训练。收敛后的模型在测试集的ROC曲线如图8所示，其AUC可达0.920 4，具有较为优秀的分类性能，这证明了前述特征提取和特征降维操作的有效性。

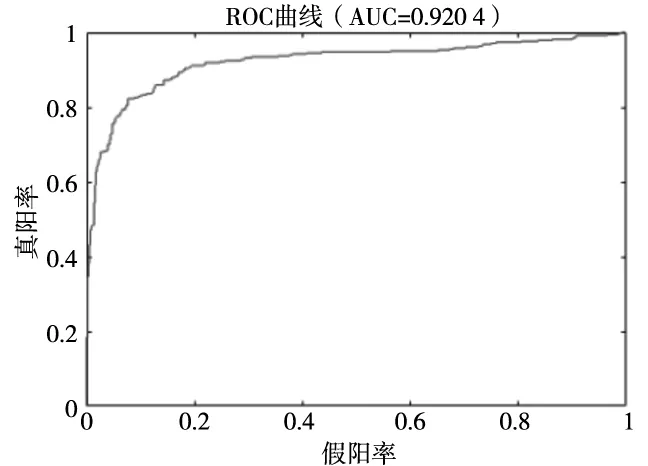
图8 模型二分类ROC曲线

2.3 LSTM识别模型的训练与测试

为了更准确的判断砂轮的磨损状态，使用LSTM来构建循环神经网络以提取样本间差异等特征。将样本数据集分为训练集(70%)和测试集(30%)，以样本对应节点为标签，以降维得到的特征为输入对LSTM网络进行训练，训练损失函数选择均方误差(Mean Suqare Error，MSE)，训练的优化器选择运行速度较快的SGD，学习率设为0.001。LSTM循环神经网络中网络参数、时间步长等超参数选取将影响网络的识别能力，设置不同超参数以训练LSTM网络并计算各超参数设置下的模型预测误差(MSE)以寻找最佳超参数组合。最终选定的误差最小的模型由4层构成：输入层，两层LSTM隐含层，一层输出层，隐含层由40个LSTM单元构成。

前面选定的LSTM网络模型经过25步训练后，训练集均方根误差收敛于0.53，均方误差收敛于0.47，在测试集上的结果如图9所示，均方根误差为0.62，均方误差为0.61。对应的最优传统BPNN网络经过1000步训练后在测试集的结果如图10所示，均方根误差为1.07，均方误差为2.30。二者的分节点测试误差如图11所示，可以看出LSTM网络模型相比BPNN模型均方误差降低了73.1%，均方根误差降低了33.6%，而且数据波动较小，结果更加稳定。在节点10 以后的砂轮磨损后期过程中，相邻帧之间的变化蕴含着更多信息，而传统神经网络由于其局限性难以对帧间差异进行特征提取。LSTM网络由于其单元特性，能够记忆相邻帧见的信息，从而对砂轮的状态做出更准确的判断。

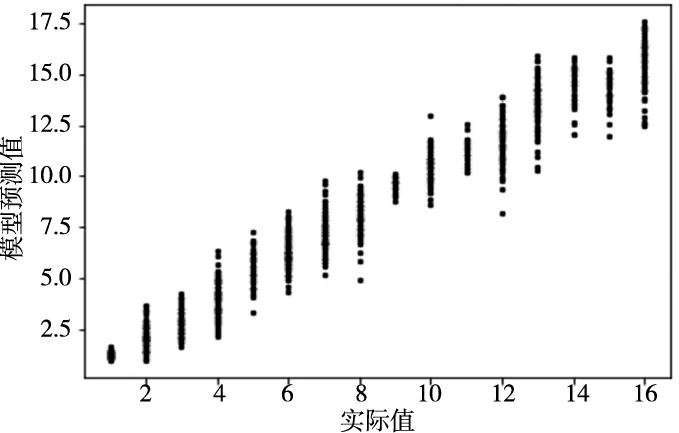
图9 LSTM网络模型预测结果

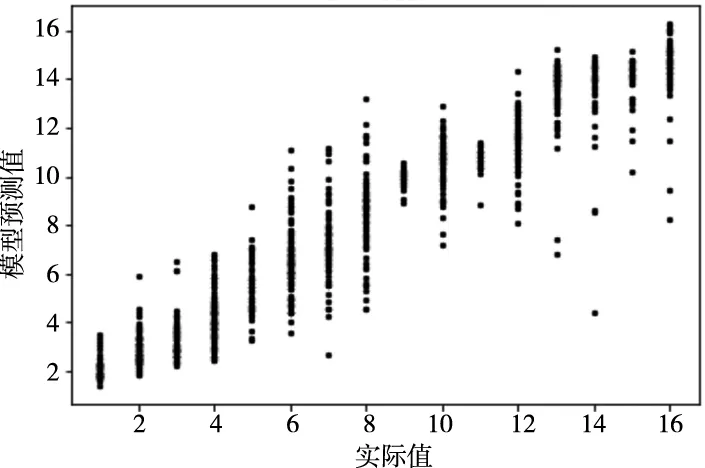
图10 BPNN网络模型预测结果

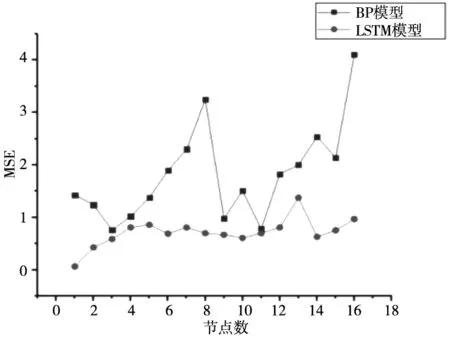
图11 模型误差比较

3 结论

本文提出了一种基于LSTM循环神经网络识别金刚石砂轮磨损状态的方法。对于从实验平台金刚石砂轮磨削熔石英实验中采集到的声发射数据，首先通过小波包分析提取了声发射信号中关于砂轮磨损状态的敏感频段特征并通过进行降维处理，从而训练LSTM循环神经网络并测试。测试结果表明，LSTM网络可以比较准确地判断砂轮的磨损状态，在16个节点的判断中MAE误差可以达到0.72，证明了LSTM模型在砂轮磨损状态识别上具有比传统神经网络更好的效果。本文验证了自然语言处理领域广泛应用的LSTM循环神经网络在砂轮磨损状态识别的实用性和有效性。本文的处理过程中没有涉及阈值选择等处理，因此较容易地推广到其他类型砂轮和刀具的状态识别应用中。