基于均方根和相关熵的测量数据筛选及应用*

段子誉，姚振强

(上海交通大学机械与动力工程学院，上海 200240)

0 引言

发动机缸盖是发动机关键的零件之一，缸盖是一种结构复杂、具有许多高精度要求的平面和孔的零件。凸轮轴承盖安装面的加工质量决定着凸轮轴孔的质量[1-3]。

加工误差是指被加工工件达到的实际几何参数对设计几何参数的偏离值[4]。产生加工误差的原因有很多，包括加工原理的误差、装夹的误差、刀具的制造误差及磨损、毛坯的误差、机床的误差等[5]。按照加工误差的表现形式，可以分为系统性误差和随机性误差两大类。系统误差又可以分为常值性系统误差和变值性系统误差。在加工一批工件时，大小、方向都不变的加工误差称为常值性系统误差[6]。常值性系统误差只要掌握误差的大小以及方向，就可以通过调整将其减小[7]。

通过测量数据，可以知道加工偏差，并依据数据，进行镜像补偿[8]。

对数据进行随机误差识别的常用方法有3σ法，箱型图法等。3σ法即判断数据是否在全部数据中均值的±3σ范围内。箱形图是数字数据通过其四分位数形成的图形化描述，高于上下触须的值认为是离群值[9]。也有使用主成分分析法对统计数据进行筛选[10]，以及通过多元质量控制，对动态数据异常值进行实时筛选[11]和基于点云数据的自由曲面加工误差评定[12]。

1 发动机凸轮轴承盖安装面加工质量分析

1.1 凸轮轴承盖安装面整体介绍

某国产某型缸盖生产线中，凸轮轴承盖安装面各小面加工不一致。某型缸盖实物如图1所示，图纸要求如图2所示，图2中画圈部分即为凸轮轴承盖安装面。

图1 某型缸盖实物

图2中，F2401、F2402、F2405、F2406、F2409、F2410、F2413、F2414、F2417和F2418为缸盖的进气侧凸轮轴轴承盖安装面，F2403、F2404、F2407、F2408、F2411、F2412、F2415和F2416为缸盖的排气侧凸轮轴承盖安装面，一共18个小面。图纸的要求如下：F2401～F2418共18个面与底面A′有着134.15 mm的高度尺寸要求。

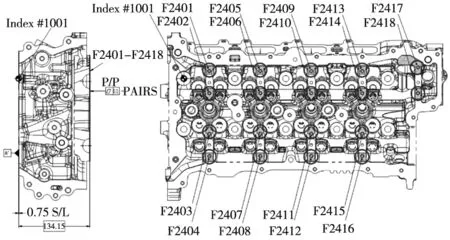
图2 某型缸盖凸轮轴承盖安装面图纸要求

18个面整体的整体偏差可以使用极差以及标准差来表示。

1.2 凸轮轴承盖安装面加工轨迹

某型缸盖中，凸轮轴承盖安装面共18个小面加工使用的是φ63的盘铣刀，加工轨迹如图3所示，图中，刀具轨迹呈S型，一列一列进行走刀，黑框代表加工时的区域，箭头代表加工时的方向。基于图3所示的加工轨迹，需要对加工的每一列进行补偿，即每一列的4个小面使用一个补偿值。对整体的横向加工误差进行补偿。

该特征需要用同一补偿值对同尺寸要求的不同小面进行补偿。

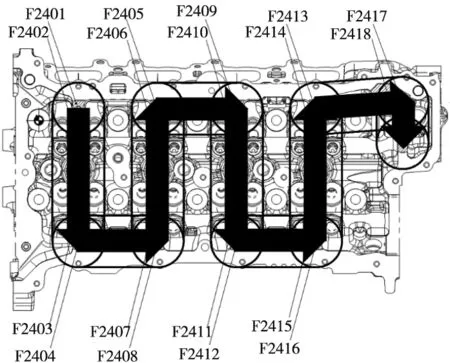
图3 凸轮轴承盖安装面加工轨迹

18个凸轮轴承盖安装面的每一个小面的面积仅占整个大面面积的0.31%，在评价的时候可以将每一个小面看做一个点。对F2400～F2417共18个面的相对理论基准的厚度测量值进行分析，通过MATLAB画出面形图和线型图如图4所示，图中每一层代表一个工件。

从图4a中可以看出，缸盖的F2401、F2402、F2405、F2406、F2409、F2410、F2413、F2414、F2417和F2418(进气侧凸轮轴承盖安装面)，F2403、F2404、F2407、F2408、F2411、F2412、F2415和F2416(排气侧凸轮轴承盖安装面)从横向看存在着中间高，两边低的凸起，凸起均存在于F2409、F2410、F2411和F2412(均在同一纵截面上)。从纵向可以看出每一列均存在着中间低，两边高的情况，且最低处为F2402、F2406、F2410、F2414和F2418(均在同一横截面上)。且各件的规律相对一致。整体存在高点低点需要进行加工补偿[13-14]。

从图4b可以看出，不同组的凸轮轴承盖安装面加工的特征趋势相对一致，不同组的数据相交的情况较少，该特征存在着常值性系统误差以及随机误差。

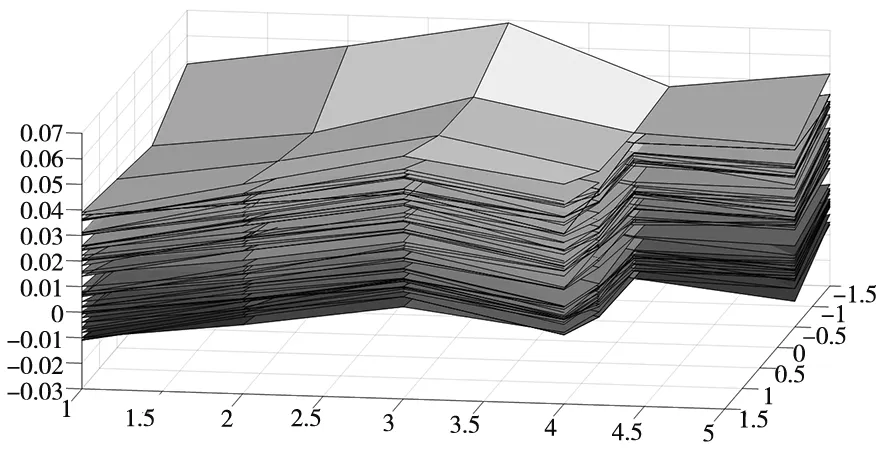
(a) 安装面面形图

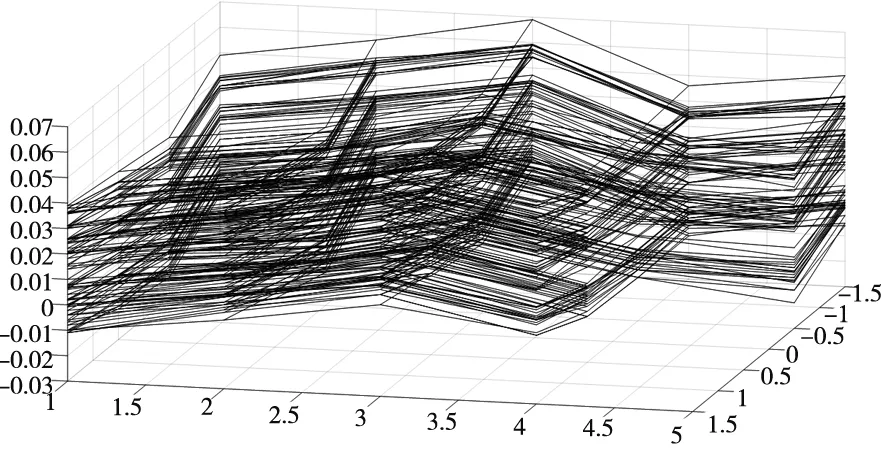
(b) 安装面线形图图4 凸轮轴承盖安装面

2 用于补偿平面的测量数据筛选

多组测量数据中存在着随机误差的数据，将带有随机误差的数据作为补偿值的计算值，会使得补偿值不能够准确对常值性系统误差进行补偿。为了使得选取的数据能够准确的表达出系统误差，需要对得到的数据进行筛选，选择出能够表达出系统误差的测量数据，并依此进行补偿值的计算。

2.1 基于均方根平面度误差的数据筛选

均方根误差是观测值与真值之间的偏差[15]。均方根平面度误差(ΔFrms)是评判面型偏差的一种评价模型，其定义为：偏离最小二乘评定基面的各局部平面度偏差平方和的平方根值。计算如式(1)所示:

(1)

式中，LFD(Local flatness deviation)为局部平面度偏差，A为平面度要素的表面面积。

均方根平面度误差越大，说明该数据偏离整体数据的程度越大，数据中存在粗大误差。

按照式(1)对平面的测量数据进行评判，可以判断出一组数据中的显著误差，即偏离整体规律的数据。并通过统计分析的方法，将其分离，筛选出整体规律一致，能够反映系统误差的数据。

2.2 基于相关熵的数据筛选

相关熵V定义为2个随机变量A和B差的高斯函数的平均值[16]，即：

V(A,B)=E[k(A-B)]

(2)

式中，k(x)为内核宽度为δ的高斯核函数，A为测量值，B为整体的最小二乘法拟合值。

当测量数据为离散量时，测量变量的标准差σ可作为内核变量。那么高斯核函数：

(3)

当两个变量的联合概率密度分布未知时，通过n个有限量作为样本时，相关熵V可通过式(4)估算：

(4)

根据最大熵原理构造相关熵估计可得最大问题：

(5)

式中，i为工件件号，j表示测量特征号，n为工件数量，m为每个工件的不同特征测量数据数量。令误差ei=Ai-B，那么

(6)

将最大值问题转化为最小值问题，可得最小值问题：

(7)

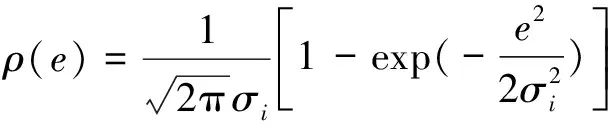
根据影响函数(IF)的定义，影响函数为估计函数的偏导，即:

(8)

从式(8)可以看出，当e→0时，影响函数与测量误差近似成正比，当e→∞时，影响函数趋近于0。即通过相关熵估计可以在数据中存在显著误差的时候识别出随机误差。

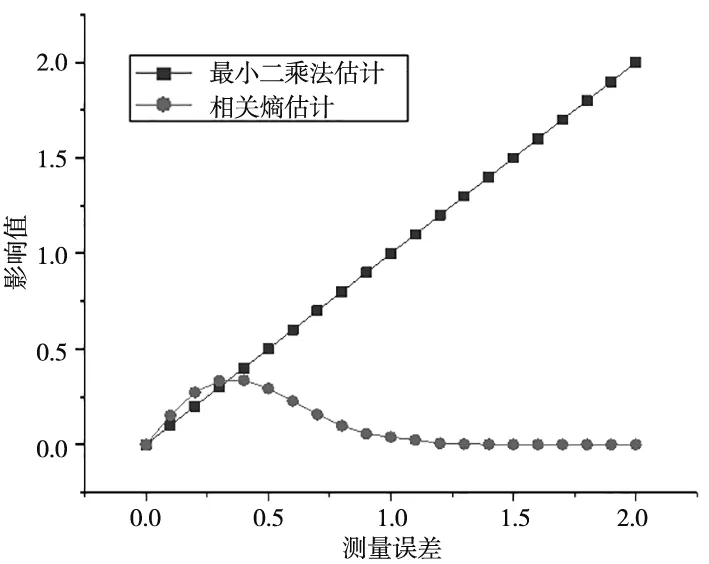
图5 最小二乘估计和相关熵估计影响系数比较图

图5可以看出，使用最小二乘估计(即2.1节所述的方法)筛选数据，可以将数据中的显著误差筛选出来；使用相关熵估计筛选数据，可以优先筛选出测量数据中的随机误差。

2.3 基于均方根平面度误差和相关熵估计的数据筛选

在实际应用中，首先使用均方根平面度误差对整体数据的显著误差进行筛选，然后利用相关熵估计的影响函数对剩下的数据中的随机误差进行筛除。留下整体数据中的系统误差，并根据筛除后的数据，进行补偿值计算。

流程图如图6所示。

图6 筛选测量数据流程图

3 基于测量值波动程度的补偿值确定

加工同一种零件时，由于加工重复精度的不同，每一个特征的加工误差存在波动。如果对一组同尺寸的平面同时进行补偿，补偿值能否对每一个面进行有效补偿尤为关键。

以加工重复性即对应测量数据的标准差为依据进行权重系数的计算，可以在一定程度上减小机床重复定位精度对补偿值可靠性以及准确性的影响。

对每一个面的厚度进行平均值与标准差的计算，如式(9)和式(10)：

(9)

(10)

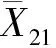
从第i列开始，按照对应每个面的标准差的大小进行排序，找到其中标准差最小的面；

ai j= min(σij)

(11)

其中，j=1,2,…,m。m为第i列的面数。

令其权重bij=1，其余面的权重用式(12)得到：

bij= (σi j-ai j)/0.0001 + 1

(12)

依此得到同一补偿值下的每一个面的权重，将所得权重转化至区间[0,1]之间，所得权重系数如式(13)所示：

(13)

加权平均数即将各测量数值乘上相对应的权重系数，然后相加求总和，最后除以总的单位数，第i列的加权平均数如式(14)所示；

(14)

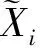
利用式(14)对各列进行加权平均计算，用得到的值对多个面进行补偿，可以减小各个面加工重复性不同对补偿值可靠性的影响。

4 实验及结果分析

4.1 实验

选择前特定件数的测量数据作为算补偿值的依据，对数据的随机误差进行筛除，筛选出能够反映整体系统误差的数据。

测量数据中，凸轮轴承盖安装面的均方根平面度误差的统计结果如图7所示，图中可以看出，存在少部分均方根平面度误差偏大的数据，将数据中的处于均值的后95%置信区间中的数据剔除剔除9组后，并用新的数据进行相对熵估计影响值计算并进行统计分析，统计结果如图8所示，将数据中的处于均值的后95%置信区间中的数据剔除，剔除2组后，得到整体规律较为一致，可以反映整体的系统误差的数据。

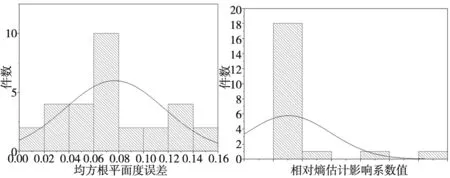
图7 初始数据均方根平面度误差分布图 图8 相对熵估计影响值分布图

选择上述所得到的数据作为算补偿值的依据。按照测量值波动程度的补偿值确定方法赋予权重，按照加工轨迹得到每一列的权重，F2401～F2404；F2405～F2408；F2409～F2412；F2413～F2416；F2417～F2418的权重分布为表1～表5所示。

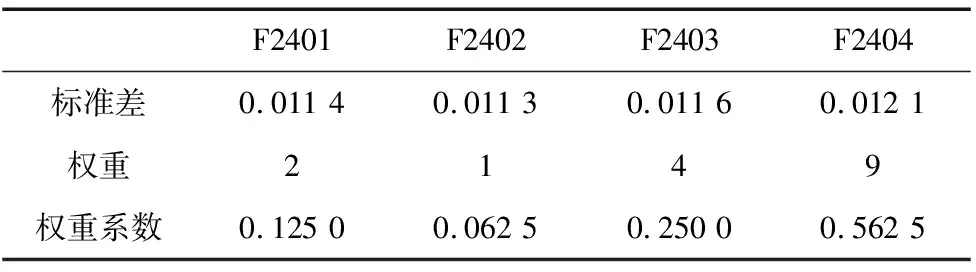
表1 F2401～F2404权重

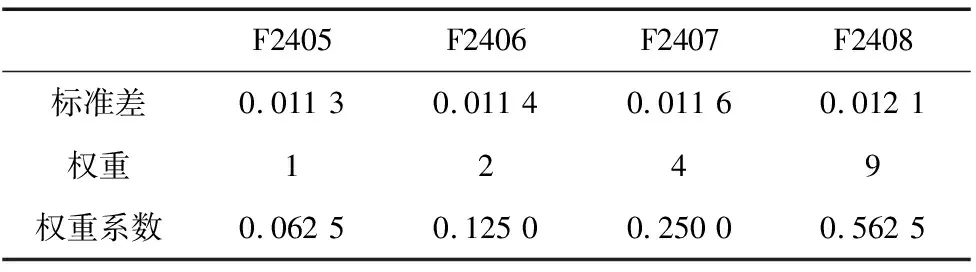
表2 F2405～F2408权重

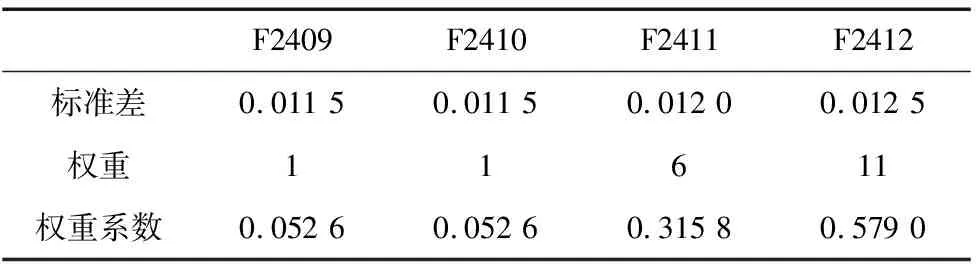
表3 F2409～F2412权重

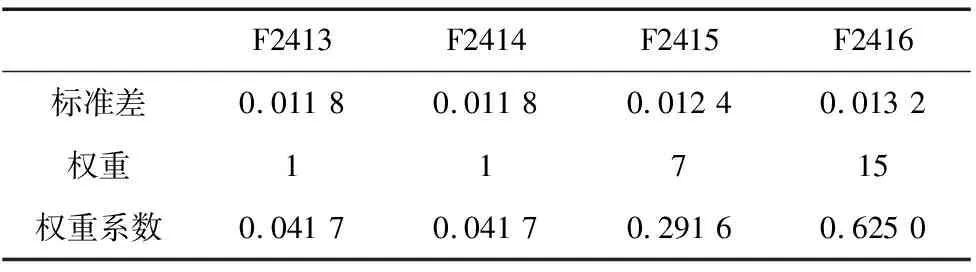
表4 F2413～F2416权重

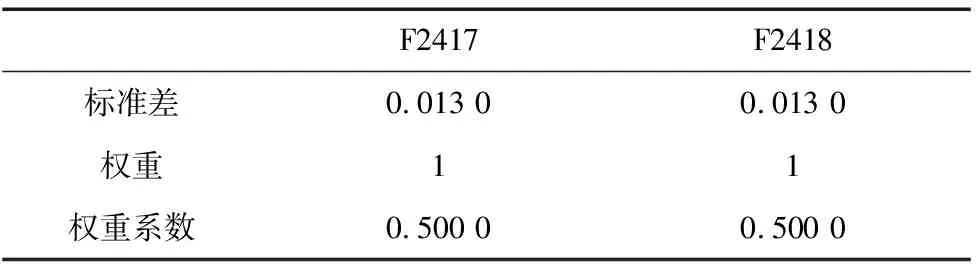
表5 F2417～F2418权重

通过对F2400～F2417共18个小面赋予相对应的权重系数，使得算出的补偿值能够对凸轮轴承盖安装面进行有效的补偿。

按照表6，对检测数据进行加权平均数的计算，并且将得到的值与设计标准值134.15 mm相减，得到每行的切深改变量，如表6所示。

表6 每列改变量 (mm)

用得到的值补偿至数控系统后，进行实验。

4.2 结果分析

图9为进行补偿前后各一组的测量数据，可以看出整体的横向误差得到减小。

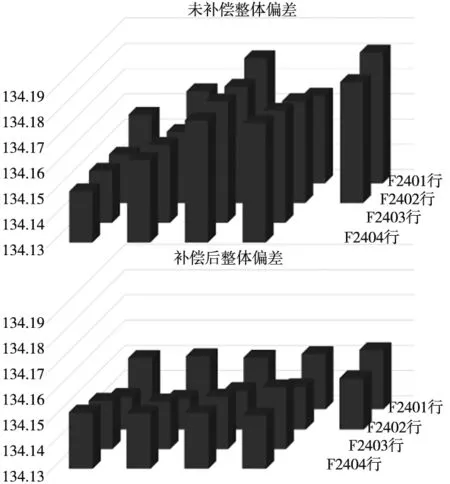
图9 改变切深前后整体高度差

整体补偿前和补偿后的折线图如图10所示，图中，横坐标表示对应18个小面，纵坐标表示测量值。补偿前的数据为数据波动大的折线，补偿后的数据为数据波动小的折线。图中可以看出，发动机凸轮轴承盖安装面各个面之间的起伏波动得到减小，且多数数据在标准值134.15 mm附近，整体平面度由0.025 8 mm降至0.008 4 mm，整体极差由0.03 mm降至0.011 mm，标准差由0.010 8 mm降至0.003 4 mm，整体偏差减小60%，整体加工质量得到显著提升。

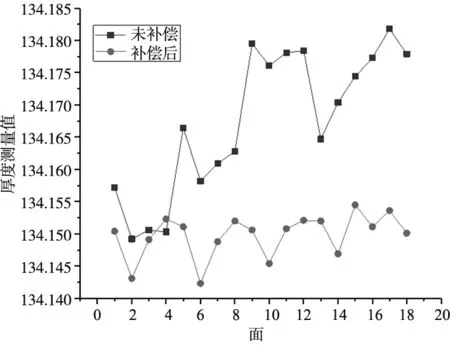
图10 补偿前后每个面的测量厚度折线图

5 结论

针对平面加工存在常值性系统误差的问题，依据大量的检测数据，通过均方根平面度误差的统计分析对检测数据进行处理，将数据中的显著误差剔除；然后，通过相关熵估计将数据中存在的随机误差剔除，通过两者结合，筛选出能够反映整体误差规律的数据。

针对用一个值对多个面进行补偿的问题，基于测量值波动程度对补偿值进行加权平均处理。使得补偿值能够有效对多个面同时进行补偿。

针对缸盖凸轮轴承盖安装面的实际问题，对大量的测量数据进行筛选，选择能够反映整体误差规律的数据，并依照加工路径，采取多个小面一起补偿的策略，使得整体18个面的整体偏差得到减小，加工质量得到显著提升。