面向电力巡检的四旋翼无人机非线性控制器设计

吴 健，花国祥，席万强，俞 斌

(1.浙江省送变电工程有限公司，杭州 310000；2.南京信息工程大学滨江学院自动化学院, 江苏 无锡 214000)

0 引言

如何提升高压输电线路巡检的精度和效率一直是制约电力行业发展的关键问题之一[1]。四旋翼无人机(下文简称四旋翼)因其携带方便、反应灵活、操控简单的优点，被大量装备到电力行业，以无人机替换人工执行电力巡检任务可极大地提高电力巡检与设施维护的效率，降低劳动强度。不过根据相关报道[2-3]，某些公司生产的四旋翼无人机经常出现“炸机”、“撞塔”或“失联”等故障，究其原因可能是控制器系统设计得不合理。另外，四旋翼是一个多输入多输出、强耦合、欠驱动的非线性系统，这些复杂的动力学特性也给高可靠性、高精度飞行控制系统的设计增加了难度。

对于飞行控制系统的设计通常分为线性方法与非线性方法两种。在线性方法中系统的输入输出满足线性关系，常见的策略有PID(Proportion integration differentiation)控制[4]、LQR(Linear quadratic regulator control)[5]、MPC(Model predictive control)[6]、LADRC(Linear active rejection control)[7]等，这些方法虽然能在一定程度解决四旋翼的飞行控制问题，但无法很好地应对外部扰动、模型内部参数摄动等问题，鲁棒性也不足。在实际电力巡检中，无人机常常会受到横风干扰，另外挂载的视觉检测设备也会改变系统原有的物理参数(如质量、转动惯量等)，这些因素就要求飞行控制系统得具有一定的抗干扰性和适应性。与线性方法相比，非线性方法是根据被控对象的输入输出数据构造出非线性控制律，它虽能更真实地描述被控对象的动态响应。例如，赵永生等针对四旋翼在外部气流干扰与内部参数不确定性下的轨迹跟踪控制问题，设计了一种基于扰动观测器的动态反演滑模控制算法，并在仿真中验证了该算法的有效性[8]。基于自适应策略解决模型参数不确定性的先验知识，文献[9]提出了自适应滑模控制器策略来解决四旋翼在极端环境下的轨迹跟踪控制问题。文献[10]结合滑模扰动观测器与反步法控制实现了四旋翼的耦合控制。由此可见，非线性控制方法着实是解决四旋翼在扰动条件或模型不确定性下的一种有效途径。

上述研究给本文面向电力巡检的四旋翼非线性控制器设计提供了借鉴。本文将四旋翼的动力学模型按照时间尺度原理分为位置回路与姿态回路，其次引入包含了外界扰动与建模不确定性的集总干扰，并分别设计了反步法-积分滑模控制方案。最后，通过理论分析与数值仿真验证了本飞行控制方法的有效性。

1 四旋翼飞行器的刚体动力学模型

本文选取的电力巡检四旋翼无人机外观为“X”字形，其简化模型如图1所示(上标e、b分别代表地球坐标系和机体坐标系)。

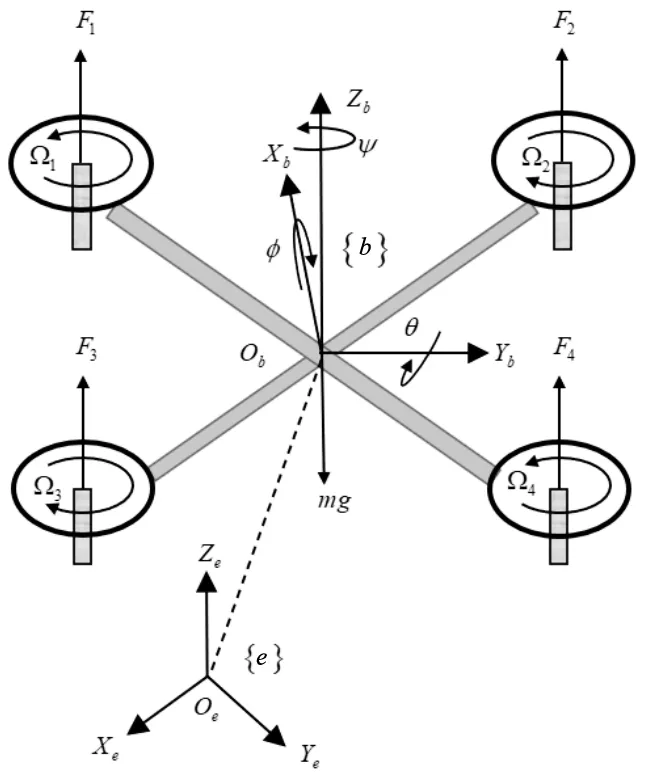
图1 电力巡检四旋翼无人机的简化模型

若将四旋翼当作一个六自由度的单刚体，并忽略桨叶的陀螺效应及空气阻力等响应，可根据牛顿-欧拉法推导出整个系统的动力学模型[11]，即：

(1)

四旋翼的运动控制是通过驱动4个桨叶实现的。桨叶转速Ωi(i=1,2,3,4)决定了四旋翼的总升力F和力矩τ，具体的计算公式为：

(2)

(3)

式中，l为桨叶中心到四旋翼质心的距离，cT和cM分别为桨叶升力系数和桨叶扭矩系数。

2 双环控制器设计

四旋翼的控制器一般分为位置环与姿态环，共包含6个控制回路(3个位置和3个姿态)，每个回路均采用反步法-积分滑模控制策略来设计控制律，具体过程如下所示。

(1)位置控制器设计

定义位置环的跟踪误差为eP=pd-p，pd为参考位置信号，结合式(1)可进一步改写位置环的动态跟踪误差为：

(4)

设计一个线速度虚拟控制量为：

(5)

式中，Kp为控制器增益矩阵。若让速度误差eV=vd-v，则有：

(6)

结合式(1)和式(6)，有：

(7)

选择积分滑模面为：

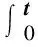
(8)

式中，t为时间，KV为控制器增益矩阵。

接着设计位置环的控制律为：

(9)

式中，αV与βV为正定的控制器增益矩阵，sign(·)是符号函数。

按照时间尺度原理[13]可知，位置环的输出是姿态环的参考输入，为了防止位置环输出信号发生“微分爆炸”，需设计微分跟踪器，这里就不再赘述微分跟踪器的设计过程。

(2)姿态控制器设计

定义姿态误差为eA，利用单位四元数的性质，对四元数求关于时间t的导数可得：

(10)

式中，ωd是参考四元数qd对应的角速度，Ψ(·)=[0,·T]T。

设计一个角速度虚拟控制量为：

ωt=eA(ωd+Kqsign(q0)qV)

(11)

式中，Kq为控制器增益。

令角速度误差eω=ωt-ω，从式(11)可得：

(12)

式中，d1是姿态环的扰动量。

选择积分滑模面为：

(13)

式中，Kω为控制器增益矩阵。

接着设计姿态环的控制律为：

(14)

式中，αω与βω为正定的控制器增益矩阵。

3 控制策略稳定性分析

控制器稳定性证明是验证控制器设计是否合理的不可或缺的一环。选择一个正定的Lyapunov函数为：

(15)

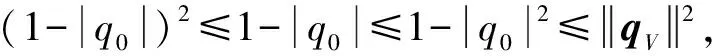
(16)

对四元数求导，有：

(17)

对式(16)求导，有：

(18)

为了简化分析，有下列不等式：

(19)

(20)

(21)

(22)

联立式(18)～式(22)，有：

(23)

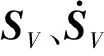
当t≥Tm=max{TV,Tω}时，有：

(24)

式中，KLa=2min{KP-0.5,KV-2.5,(Kq-2.5)/2,Kω-0.5}。若控制器参数满足：KP>0.5，KV>2.5，Kω>0.5，则有：

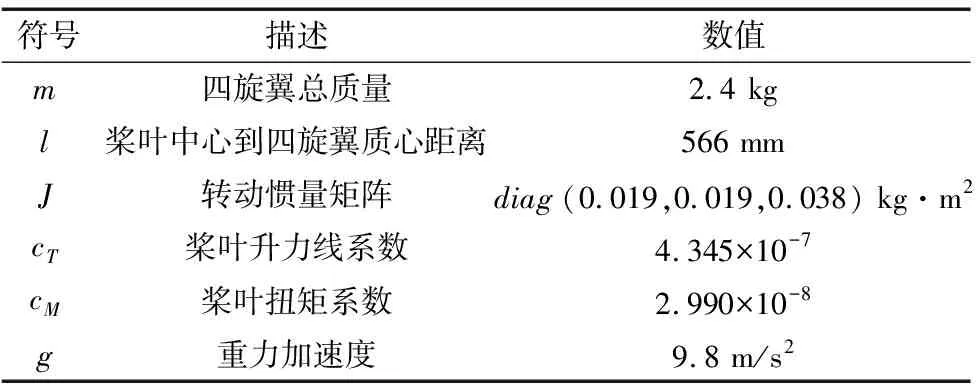
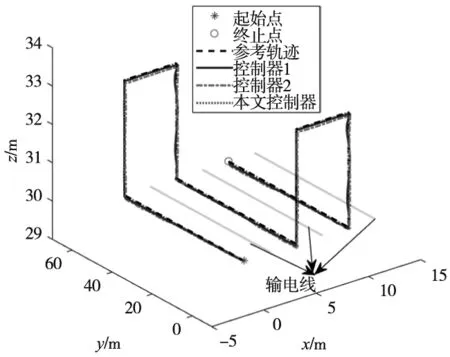
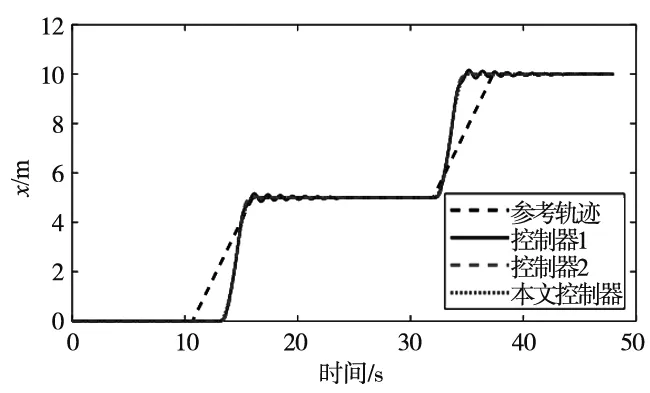
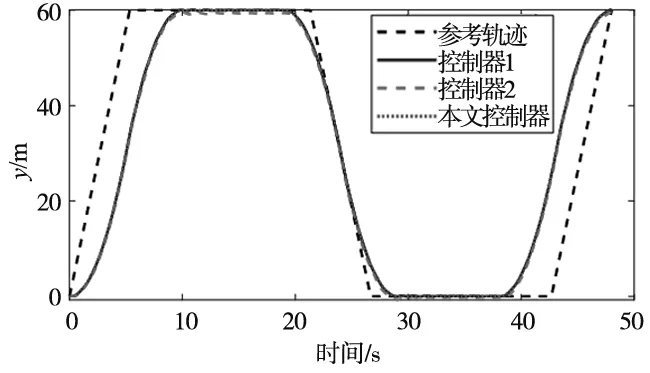
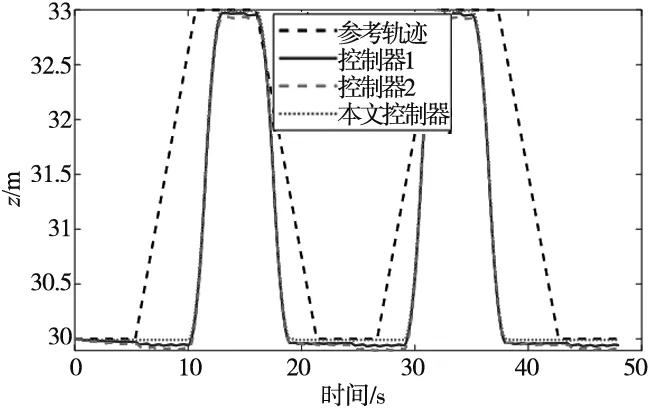
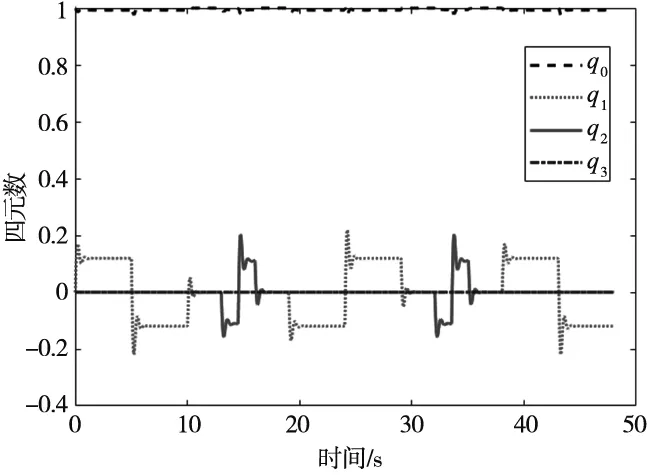
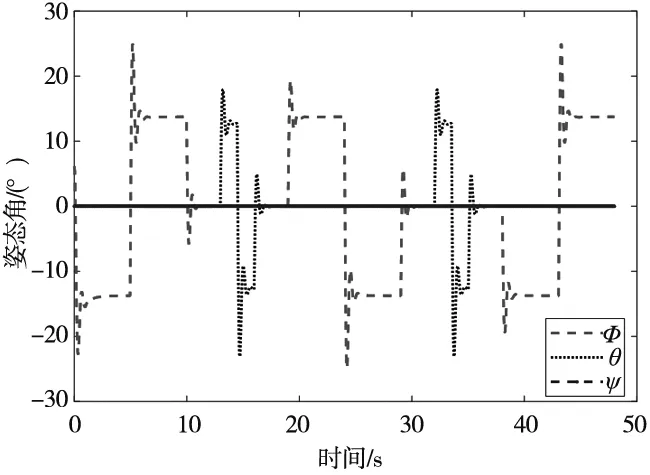
L

(25)

式中，tl=t-Tm≥0。四旋翼的误差eP、eV、eq和eω能渐进收敛至0，故系统是稳定的。

4 仿真结果

本仿真中涉及的电力巡检四旋翼无人机的物理参数如表1所示。仿真环境为MATLAB2020b/Simulink平台，PC机的配置为i7-10875H双核。接下来通过一个算例来验证本文所提控制方法的有效性。

表1 电力巡检四旋翼无人机的物理参数

仿真模拟的是四旋翼对直线型塔杆电线巡检，相邻两座电塔间连接着3根输电线缆，每根电缆之间的距离为50 m，电缆长度为60 m。要求四旋翼从起始点出发逐次巡检3根线缆，飞行速度为6 m/s。另外，为了评价本文控制器的性能，引入反步法-动态滑模控制(控制器1)、反步法-终端滑模控制(控制器2)进行对比(这两种控制器的设计参考文献[14-15])。本文控制器参数的设定如表2所示。

表2 本文控制器参数设定

四旋翼的参考飞行路径为(0,0,30) m，(0,60,30) m，(0,60,33) m，(5,60,33) m，(5,60,30) m，(5,0,30) m，(5,0,33) m，(10,0,33) m，(10,0,30) m，(10,60,30) m。另外，偏航角为0，飞行过程中不作控制。为了模拟集总干扰，在位置环加入均值为0、方差为0.01、频率为50 Hz的随机噪声。整个仿真过程历经48 s，结果如图2～图5所示。其中，图2给出了三种控制器下四旋翼电力巡检的飞行轨迹，可以看出三种控制器都能实现对参考航迹的跟踪。

图2 三种控制器下的三维航迹比较

图3展示了3个位置通道的响应曲线。从图3c可以明显看出，本文控制器比其他两种控制器具有更高的跟踪精度与抗干扰能力。为了更清晰地展示X、Y和Z方向上的跟踪误差，引入平均误差(Mean error，ME)和均方根误差(Root mean square error，RMSE)来评价三种控制器的控制性能，结果如表3所示。从结果可以看出，无论从ME还是RMSE来看，本文控制器的性能均要优于其他两种控制器，例如以y通道为例，本文控制器对应的ME值分别比其他两种控制器低了27.27%和14.29%，RMSE值分别低了63.33%和15.38%。综述结果说明了反步法能够提高闭环系统状态量的收敛速度，积分滑模能有效抑制系统的集总干扰。

表3 三种控制器性能比较

(a) X方向的响应

(b) Y方向的响应

(c) Z方向的响应图3 四旋翼无人机位置环的响应

图4和图5给出了在本文控制器下四旋翼姿态角的响应，其中前者是四元数随时间的变化，后者是经数学变换后的三个姿态角随时间的变化。这里需要补充的是，由于控制器的不同导致位置环输出量不同，进而导致姿态环的参考量也不同，故姿态环无法给出三种控制器性能比较。

图4 四元数响应

图5 姿态角的响应

5 结束语

本文提出了一种基于反步法-积分滑模控制策略，用来解决面向电力巡检的四旋翼无人机在集总干扰下的巡线跟踪控制问题，主要得到结论如下：

(1)本控制器中的反步法能够提高闭环系统状态量的收敛速度，积分滑模能有效抑制系统的集总干扰；

(2)与反步法-动态滑模控制与反步法-终端滑模控制相比，本文控制器的控制精度更高、抗干扰能力更强；

(3)本文所设计的控制器能够有效解决四旋翼电力巡检问题。