城市路网中电动汽车充电站双层多目标选址定容模型
武渊,叶宁
(1. 山西省人事考试中心,山西 太原 030006;2. 南京邮电大学 计算机学院,江苏 南京 210042)
0 引言
目前,全球能源短缺和温室气体排放问题日益显著。作为人口和制造业大国,我国的能源消耗和二氧化碳排放量不容忽视。据英国石油公司统计,2016 年中国一次能源消费达30.53 亿吨石油当量,占世界一次能源消费总量的23%,由此产生的二氧化碳排放量达91.23 吨,占世界总排放量的27.3%。针对上述问题,我国在《巴黎协定》和“十四五”规划中做出在2030 年实现“碳达峰”、2060 年实现“碳中和”的承诺。为实现上述目标,在交通领域大力发展具有污染小、噪声低等特点的电动汽车(Electric Vehicle,EV)成为必然趋势。然而,由于电池续航里程不足,充电时间长以及充电站建设又不完善等问题,电动汽车的发展受到了极大制约[1]。因此,如何合理规划充电站位置及容量,以满足道路交通需求已成为城市绿色交通发展的关键问题。
目前,国内外学者已针对电动汽车充电站选址定容问题开展了相关研究。蔡子龙等[2]总结了应急充电站的选址影响因素指标体系,并基于层次分析法-目标规划法提出了一种应急充电站选址模型。吴雨等[3]以充电站年总成本最小为目标,提出了一种基于改进免疫克隆选择算法的电动汽车充电站选址定容方法。赵炳耀等[4]建立了一种高维非线性的充电站选址定容模型,并通过Voronoi 图和改进引力搜索算法联合求解。Wang 等[5]考虑了电动汽车的充电时间、定位能力,以最小化运行成本为目标优化了充电站位置。Chen 等[6]将停车需求,土地属性,人口密度和出行需求为约束,以降低电动汽车用户的使用成本为目标,确定了充电站的最佳位置。Gagarin 等[7]提出根据经济因素,工程可行性,服务可用性,社会因素,环境因素和土地因素标准对候选站点进行综合评估,进而筛选出最佳充电站位置和容量。
上述文献大多针对现有的用户需求,并未挖掘用户充电行为和充电站建设方案之间的关系,从而忽视了用户充电需求的潜在变化。实际中,用户会根据充电站的建设位置和容量情况,自主调整充电决策方案,即充电站建设方案与用户使用情况具有反馈关系。针对上述问题,近年来,少数学者考虑上述反馈关系,提出了同时从政府和用户角度充电站选址定容方案。由于充电需求模式的变化是在给定充电站建设方案之后确定的,这些研究大多采用双层规划的思路,并通过相应的启发式算法(如粒子群算法)进行求解[8-10]。
然而上述研究仍存在以下三点缺陷:
1)实际中,充电站作为大功率设施,其建设往往需要对接入电网进行扩建和改造,即充电站的建设将产生一定的电网扩展成本。另一方面,由于地域和用地规划影响,电网并不能无限制扩建,即电网容量存在上限,而现有研究并未考虑电网容量的限制和扩展成本;
2)充电站的服务质量与该地区电动汽车的发展息息相关,若服务质量较差,则用户更倾向于购买传统燃油汽车,并不符合“碳中和”的社会需求;若服务质量较好,则用户更倾向于购买电动汽车,有利于减少碳排放。然而现有研究大多仅以经济效益为目标,缺乏对地区服务质量方面的考量;
3)算法的精确度直接影响优化结果,因而开发高效精确的算法尤为重要。现有研究大多采用遗传、粒子群等原始算法,未针对问题提出改进算法。
本文针对上述问题,以最小化充电站建设成本和最大化充电站服务质量为目标,考虑电网容量的影响,建立了充电站选址定容多目标双层规划模型,并提出了一种基于混沌理论的NSGA-II 算法(CNSGA-II)对上述模型进行求解。最后通过仿真分析和对比实验,验证了CNSGA-II 算法求解充电站选址定容多目标双层规划模型的有效性。
1 充电站选址定容多目标双层规划模型
本文利用图论的方法,将城市地区道路交通主干道抽象为一张网络图G=(V,A),其中V为网络图G中的节点集合,A为节点之间路径的集合。为便于建模求解,本文假设V为备选充电站地址,且扩建电网能够满足用电需求。
上层模型即从政府的角度出发,以最小化充电站运行周期内的综合成本和最大化服务质量为目标,优化充电站位置和规模(即充电桩数量)。
下层模型即从用户的角度出发,在给定充电站位置和规模的情况下,以最小化充电成本为目标,优化充电站选择策略。
1.1 上层模型目标函数
充电站建设需要尽可能减小充电站运行周期内的综合成本,同时考虑到充电站的服务属性,应尽可能提高服务质量。其中,综合成本包括土地成本、充电站建设成本,设备维护成本和用户使用成本。此外,由于充电站是高功率电力设施,电网扩展成本同样不容忽视。本文中,服务质量量化为充电站的覆盖范围,覆盖范围越大,服务质量越高。
1.1.1 综合成本
综合成本即为土地成本(CL)、充电站建设成本(CR)、设备维护成本(CG)、电网扩展成本(CK)以及用户使用成本(CU)之和,表述如下:

其中考虑到用户将根据路网结构和充电站位置改变充电策略,用户使用成本(CU)在下层模型中给出,其余各项成本的计算方式如下:

式中:cl为单位充电桩的土地成本;xi为二元变量,xi=1 表示在第i个节点建充电站,反之,xi=0 表示不在第i个节点建充电站;Ni为在第i个节点建立充电站的规模,即充电桩个数;cr1和cr2分别表示建立充电站的固定成本和每个充电桩的投资成本;cg1,cg2和cg3分别表示建立充电站系统的每日固定维护成本,每个充电桩的固定维护成本和与充电负荷相关的可变维护成本;T为规划周期内的时段数;PLi为第i个节点的t时段的电力负荷;ck表示电网的单位容量扩展成本;fi是第i个节点的充电电流;RPi是第i个节点的额定功率负载;IPi是第i个节点施工之前的额定电力负载。
1.1.2 服务质量
如前所述,本文采用充电站覆盖范围量化服务质量。由于城市路网可以看作线路和节点的组合,难以直接通过服务半径衡量充电站服务范围。因此,本文使用同一条道路上相邻两个充电站之间的平均距离来表示覆盖强度,数学描述如下:

式中:α是将节点之间的距离转换为实际距离的参数;d(xi+1,xi)表 示 节 点i+1 和 节 点i的 点 对 点距离。
1.2 上层模型约束条件
1.2.1 需求约束
在服务区域内,充电站容量不应小于该区域内电动汽车的总充电需求。

式中:Lmax表示该地区电动汽车的总充电需求。
1.2.2 距离约束
假设充电车辆仅在充电站接受充电服务,直到充满电位置。因此,两个相邻充电站节点间的距离不得大于平均最大行驶距离。

式中:Dmax是电动汽车在电池充满电后的平均最大行驶距离。
1.2.3 规模约束
在实际建设过程中,受土地面积和充电质量需求的影响,不允许充电站的规模过小或过大。因此,对于任一xi=1 的节点,其充电站规模具有以下约束:

1.3 下层模型目标函数
下层模型主要从用户角度出发,优化目标为用户综合成本,决策变量为充电策略。其中,充电策略即为电动汽车在特定时刻选择充电站进行充电操作的方案(ψ(v,xi,t)),用户综合成本包括充电成本(C1)和用户从当前位置抵达充电站的驱动成本(C2),以及充电负荷需求未满足的损失成本(C3)可表述如下:
各项成本的计算方式如下[10-11]:

式中:εi,t为t时段的单位充电电价;tv为电动汽车v在时段t内的充电时长;dv,i为车辆初始位置至充电节点i的最短距离;ψ(v,xi,t)为二元函数,当电动汽车v于时刻t在充电站xi充电时,ψ(v,xi,t)=1,反之,为0;c2和c3分别表示单位距离的驱动成本和单位负荷未满足的损失成本;PLi,tloss表示未满足的充电负荷需求。
1.4 下层模型约束条件
1.4.1 可达充电站距离约束
电动汽车的电池电量有限,因此,对于任意电动汽车,均存在最大可达充电站距离约束,表述如下:式中:Dv,max为电动汽车v的最大行驶距离。

1.4.2 充电电量约束
本文将充电电量设为电动汽车从出发位置至充电站的电量消耗,表述如下:

1.4.3 容量约束
优化后的所有充电站在对应的充电计划之下,各个充电站节点的充电负荷加上未满足的充电负荷需求等于该节点的容量配置,该约束为:

1.5 综合模型
整合上层和下层模型的目标函数及约束条件,即可得出电动车充电站多目标选址定容双层规划模型:

其中,ψ由下层模型得出,可转换为

约束条件即为上层和下层模型约束条件的集合。
根据式(17)和(18)可以看出,下层模型本质上可以归约为上层模型的一个等式约束,即上层模型的求解依赖于下层模型的优化结果。若给定一组选址定容方案,首先,需要输入至下层模型求解,并将其结果(即用户使用成本)输入至上层模型。因此,所建立的上下层模型存在反馈关系。由此,即可计算出给定址定容方案对应的综合成本和服务质量目标函数值。若采用枚举方法,即将可能的选址定容方案的目标函数值均按照上述过程计算得出,既可以通过Pareto 非支配理论,比较得出最佳折中解。
然而,复杂的路网结构往往存在巨量的选址定容方案,枚举方法对于海量解空间搜索效率较低。因此,需要开发一套有效的充电站选址定容多目标优化算法。
2 基于改进CNSGA-II 的充电站选址定容多目标优化算法
如前所述,充电站选址定容下层模型可归约为路径规划问题,进而通过Floyd 算法求解。而上层规划模型是一个多目标优化问题,可通过NSGA-II(快速非支配排序遗传算法II)求解。作为遗传算法(GA)的多目标形式,NSGA-II 算法具有收敛性好,鲁棒性强等优点,已被广泛应用于各种选址和调度优化问题中[12-14]。本研究在传统NSGA-II 算法的基础上,引入混沌序列,以增强算法的寻优能力和收敛速度。此外,本文采用TOPSIS 算法(逼近理想解排序方法)从NSGA-II 算法产生的Pareto 最优解集中筛选出最佳折中解。本文所设计的算法框架主体结构如图1 所示。

图1 算法整体框架结构图Fig. 1 Overall framework structure diagram of algorithm
2.1 改进的CNSGA-II算法
传统NSGA-II 算法的初始种群是随机生成的,并且交叉和变异过程也是随机执行的,降低了收敛速度。本研究将混沌序列引入NSGA-II,以解决第1 节中所建立的多目标优化模型。
本文所提出CNSGA-II 算法详细步骤如下:
步骤1(产生混沌初始解):使用一维logistic 映射方法产生基于混沌序列的初始种群。混沌是一种随机行为,具有灵敏性,遍历性和随机性的特征[15]。基于混沌序列产生的初始种群同样具有上述特征,从而能够提高算法迭代初期种群的多样性。对于实数编码的连续性变量而言,初始种群是在决策变量的上限和下限内生成的浮点数,其中混沌序列取代了随机成分:

式中:Xj,i表示第j个体的第i个染色体位置对应的变量,整形变量对其取整即可;M为种群规模。UBi和LBi分别表示第i个染色体位置对应变量的上限和下 限;τj,i表 示 混 沌 序 列,可 根 据 以 下logistic 映 射生成:
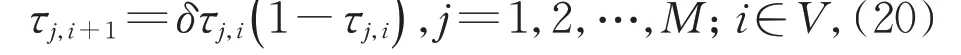
式中:δ等于4 时,将完全混沌序列。τj,1是初始随机混 沌 变 量,其 范 围 在0 至1 之 间,并 且τj,1不 等 于{0.25,0.50,0.75},因为这些初始值导致式(20)产生确定数值[15]。混沌序列中的每个值都依赖于初始值,初始值的微小变化会导致其长期行为的巨大差异,这是混沌的基本特征。因此,生成的初始种群是一个混沌序列,具有混沌特性。
步骤2(适应度计算):将每个个体具有的选址(xi)和定容(Ni)变量传递给下层模型,并调用Floyd算法计算下层模型(式(10)-(16))的最优解,反馈给上层模型。结合式(1)-(6)计算种群中每个个体的适应度值。
步骤3(基于非支配排序和拥挤度距离的个体排序):根据适合度值和个体的非支配性对染色体进行分类并排序。例如,个体a的综合成本(F1)小于个体b,且个体a的服务质量(F2)不小于个体b,则称个体a支配个体b。若个体a不被其他个体支配,则称个体a为非支配个体。拥挤度距离的详细解释参见文献[16-18]。
步骤4(选择、混沌交叉和变异操作):按照排序选择出部分个体进行混沌交叉和混沌变异操作。

式中:βi为第i个染色体位置对应变量的交叉扩展因子,可通过下式得出:

式中:η为交叉的分布指数,η较大时,将产生“近亲”子代。在传统NSGA-II 算法中,hi是随机生成的0-1 区间内的浮点数,而本文则采用类似于式(20)的混沌映射生成hi。
同理,本文对变异策略进行了改进,提出了一种基于混沌序列的改进突变策略。对于一个给定的个体X1,i,其变异个体X*1,i表述为:

式中:θi为第i个染色体位置对应变量的变异扩展因子;γi为混沌映射生成的0~1 区间内的浮点数;φ表示变异的分布指数。
步骤5(种群合并和选择子代操作):合并当前父代和子代作为一个种群,对合并种群执行步骤3和4,筛选出子代个体。
步骤6(结束判断指令):判断当前迭代次数是否达到最大迭代次数,是,算法结束,并输出Pareto最优解集;否则回到步骤5。
2.2 TOPSIS算法
NSGA-II 算法生成的Pareto 最优解集包括许多非支配解,并且每个解都有两个属性(综合成本和服务质量)。因此,从Pareto 最优解集中筛选出折衷解决方案是一个多属性决策问题。层次分析法(AHP)和与逼近理想解法(TOPSIS)是解决多属性问题的两种主要方法,已被应用于各种问题中[21-23]。与TOPSIS 相比,AHP 常用于确定属性的权重。此外,TOPSIS 是根据人类的决策过程提出的,具有强大的逻辑基础和简单的计算过程[24]。因此,在本研究中选择TOPSIS 从Pareto 最优解集中筛选出权衡解决方案。
对于具有W个解的给定的Pareto 最优集S,S=[S1,S2,…,Si,…,SW],每个解的目标可以表示为Yi=[yi1,yi2,…,yij,…,yiZ],其中Z是目标数量。TOPSIS 算法的主要步骤如下:
步骤1:将目标函数值映射到[0,1]区间,以消除量纲影响。

步骤2:定义权重向量[λ1,λ2,…,λj,…,λZ],其中λj(λj≥0)表示决策者对目标j的重视程度。权重向量的总和等于1。
步骤3:根据式产生正(S+)理想解和负(S-)理想解,如下所示:

步 骤4:计 算 偏 好 向 量D=[D1,D2,…,1Di,…,DZ],其中Di表示解决方案i的质量。 最佳折衷解决方案即为具有最小偏好Di的解决方案,表示如下:

2.3 Floyd算法
由于路网被抽象为无向图,电动汽车在路网拓扑图中选择充电站进行充电操作实质上是一个与时段相关的最短路问题,其最优方案可通过Floyd算法得出[25-26]。实质上,Floyd 算法已经被应用于求解路网中最短路径的求解,并验证了其合理性[25]。此时,充电站的选址定容方案已由CNSGA-II 算法生成,Floyd 是一种动态规划算法,其状态转移方程如下:H[m,n]=min{H[m,l]+H[l,n],H[m,n]},(30)式中:H[m,n]为给定电动汽车从初始位置m到节点n的 最 小 成 本;l为m和n之 间 的 断 点;初 始 时,电动汽车位于m节点,即H[m,m]=0。
对于任一电动车辆在任意t时刻,Floyd 算法求解下层模型的具体步骤如下:
步骤1:初始值设为H[m,m]=0;
步骤2:根据式(10)-(13)和(30),计算初始位置到下一节点的最小成本;
步骤3:判断是否抵达充电节点,是则输出充电节点n对应的成本;否则,返回步骤2;
步骤4:枚举CNSGA-II 算法生成的所有充电节点,并对比其成本。选择出具有最小成本的充电节点,即为下层模型的求解结果。
3 算例分析
3.1 路网和相关参数设置
本文以西安市的道路交通干线路网为例(如图2 所示),将所建立模型和算法应用于该城市路网,优化电动汽车充电站的选址和容量。所选地区的路网干线拓扑结构如图3 所示,其中,节点之间采用直线连接,而实际路网中节点之间并不一定是直线。实际计算时,使用真实的路网节点距离,且所有节点均为待选充电站建设节点,模型中主要参数如表1 所示。

表1 模型中主要参数Table 1 The main parameters in the model

图2 西安市干线实际路网图Fig. 2 Actual road network map of Xi′an arterial road

图3 西安市路网干线拓扑结构图Fig. 3 Topological structure diagram of Xi′an arterial road network
经过多次仿真实验,选择表现较好的CNSGAII 算法相关参数,并假定综合成本和服务质量同等重要,算法参数如表2 所示。
3.2 选址定容方案结果及分析
将上述参数和路网结构输入所建立模型,并通过所提出的算法框架求解,所得出的Pareto 前沿如图4 所示,其中充电站平均距离即为服务质量的表征量。该模型得到最佳折中解近似位于Pareto 前沿的中间位置,且距离正理想解较近,离负理想解较远,这说明本文算法得到的结果是综合成本和服务质量的有效折中。表2 列出了最佳折中解的相关参数,即选址定容方案。

图4 Pareto 前沿Fig. 4 Pareto front

表2 各算法的参数设置Table 2 Parameter setting of each algorithm
从表3 可以看出,该地区共需配置6 个充电站,结合路网可以看出,充电站大致离散的分布于城区内部的路网节点,这是由于内部节点的车辆较多,充电需求更大。

表3 所选地区充电站的选址定容决策方案Table 3 Decision-making plan for location and capacity of charging stations in selected areas
3.3 算法的稳定性分析
本文使用M-index 方法进一步测试CNSGA-II算法的稳定性和有效性,M-index 是衡量所设计的多目标优化算法搜索到的Pareto 解与问题的理论Pareto 解集之间差距的指标,在数学上定义为:
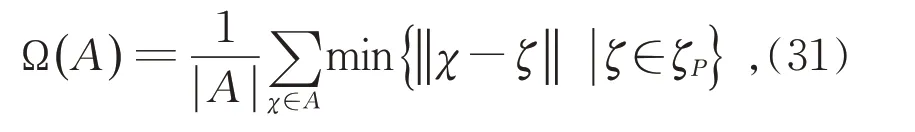
式中:Ω(A)即为算法产生的Pareto 解集和理论Pareto 解集之间的差;A是算法产生的Pareto 最优解集;|A|是A集合中非支配解的个数;||χ-ζ||为算法产生的非支配解χ和理论非支配解ζ之间的欧式距离;ζP为理论Pareto 最优解集。
表4 列出了独立进行15 次M-index 试验的结果,可以看出CNSGA-II 产生的Pareto 最优解集和理论Pareto 最优解集的偏差均值为5.753,在10 以内,差别较小。因此,所提出的CNSGA-II 算法在求解电动汽车充电站双层多目标规划选址定容模型时,具有较高的可靠性及有效性。

表4 15次M-index分析的试验结果Table 4 15 times of test results of M-index analysis
3.4 算法的对比分析
Pareto 前沿的收敛性是衡量多目标优化算法的优越度的重要指标。目前,常用的多目标算法主要包括包括NSGA-II 算法、多目标粒子群算法(MOPSO)、多目标差分进化算法(MODA)。为验证本文算法的优越性,则需与上述算法进行结果对比。由于上述算法具有一定的随机性,因此,需要独立执行多次,从统计学的角度分析各算法的优劣。
假设两种算法a与b对上述多目标优化模型执行N次所得到的Pareto 最优解集为Ai和Bj(i,j=1,2,…,N)。即可根据式(32)计算两种算法的平均控制率DR。


式中:χa和χb分 别为Ai和Bj中的元素;χa≺χb表示χa支配χb。若DR(a,b)>DR(b,a),则表明算法a得到的Pareto 最有解集支配算法b的结果,即算法a收敛性优于算法b。
对各算法独立执行20 次,计算平均控制率DR结果如表5 所示。可以看出,DR(CNSGA-II,MOPSO),DR(CNSGA-II,MODA)和DR(CNSGA-II,NSGA-II)均高于对应的元素翻转DR。这表明本文算法的收敛性优于其他三种方法。这也证明将混沌映射引入NSGA-II 算法能够显著提高其收敛性能。

表5 平均控制率DR计算结果Table 5 DR calculation results of average control rate
4 结语
本文采用二层规划模型和多目标优化理论,建立了充电汽车选址定容模型。并开发了一套以改进的CNSGA-II 算法和TOPSIS 求解上层模型,Floyd 算法求解下层模型的综合求解方法。其中下层模型计算所需的选址定容方案由上层模型算法产生,并将求解结果反馈给上层模型算法。因此,所构建的综合求解方法具有强耦合的特性。仿真算例表明所建立的模型和算法具有良好的可靠性和有效性,适用于城市路网充电站选址定容问题。此外,所提出求解方法同样可以迁移至其他双层规划求解问题中,具有广阔的应用前景。

